浙教版数学七年级上册第一章有理数 专题:数轴与绝对值(word版,含答案)
文档属性
| 名称 | 浙教版数学七年级上册第一章有理数 专题:数轴与绝对值(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 84.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-02 05:10:06 | ||
图片预览




文档简介
专题:数轴与绝对值
一.选择题
1.
如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在( )
A.
在点A,B之间
B.
在点B,C之间
C.
在点C,D之间
D.
在点D,E之间
2.在数轴上表示数-1和2020的两点分别为A和B,则A和B两点间的距离为( )
A.2019
B.2020
C.2021
D.2022
3.如图,在数轴上-4,-1的对应点分别是A、B,而A是线段BC的中点,则点C所表示的数是( )
A.
-7
B.
-8
C.
-9
D.
-10
4.
对任意有理数a,在式子1-|a|,|a+1|,|-1|+a,|a|+1中,取值不为0的是( )
A.
|a|+1
B.
1-|a|
C.
|a+1|
D.
|-1|+a
5.
如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2020将与圆周上的哪个数字重合(
)
A.
0
B.
1
C.
2
D.
3
6.
如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点可能是( )
A.M或R
B.N或P
C.M或N
D.P或R
7.
满足|a-b|+ab=1的非负整数(a,b)的个数是( )
A.
1
B.
2
C.
3
D.
4
8.
已知x的取值能使|x-3|+|x+2|取得最小值,则所有中整数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
二.填空题
9.
甲、乙两队进行拔河比赛,标志物先向乙队方向移动了0.2m,又向甲队方向移动了0.5m,相持一会儿,又向乙队方向移动了0.4m,随后又向甲队方向移动了1.3m,在大家的欢呼鼓励中,标志物又向甲队方向移动了0.9m,若规定标志物向某队方向移动2m该队即可获胜,那么获胜的队是____.
10.
在数轴上,A、B是两个定点,A表示1,B表示-4,P到A、B的距离和为7,则P表示的数是____.
11.已知|a|=5,|b|=3,且|a-b|=b-a,那么a+b=_.
12.
设a+b+c=0,abc>0,则的值是______.
13.
已知实数x满足|2x+1|+|2x-5|=6,则x的取值范围是____.
14.
如图表示数轴上四个点的位置关系,且它们表示的数分别为p,q,r,s.若|p-r|=10,|p-s|=12,|q-s|=9,则|q-r|的值
15.
李老师从拉面的制作受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段AB,对折后(点A与B重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段AB上的,均变成,变成1,等).那么在线段AB上(除A,B)的点中,在第二次操作后,恰好被拉到与1重合的点所对应的数之和是____.
三.解答题
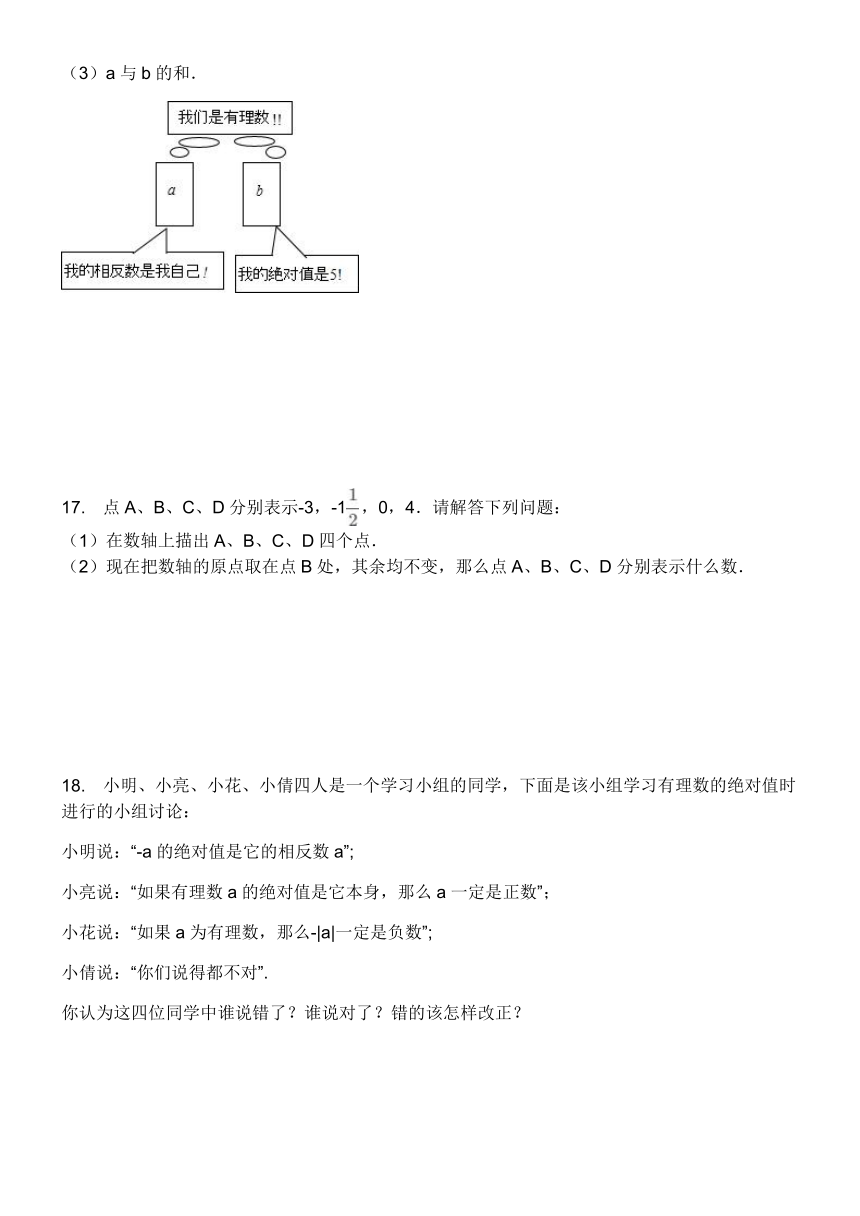
16.
读如图提供的信息,回答下列问题.
求:(1)a的值;
(2)b的值;
(3)a与b的和.
17.
点A、B、C、D分别表示-3,-1,0,4.请解答下列问题:
(1)在数轴上描出A、B、C、D四个点.
(2)现在把数轴的原点取在点B处,其余均不变,那么点A、B、C、D分别表示什么数.
18.
小明、小亮、小花、小倩四人是一个学习小组的同学,下面是该小组学习有理数的绝对值时进行的小组讨论:
小明说:“-a的绝对值是它的相反数a”;
小亮说:“如果有理数a的绝对值是它本身,那么a一定是正数”;
小花说:“如果a为有理数,那么-|a|一定是负数”;
小倩说:“你们说得都不对”.
你认为这四位同学中谁说错了?谁说对了?错的该怎样改正?
19.
对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点,沿x轴平移1个单位,得到点P的对应点P′,如图,若点A表示的数是-3,点B′则是通过上述操作后得到的点B的对应点,点B′表示的数是2,试求线段AB的长.
20.
用字母a表示一个有理数,则|a|一定是非负数,也就是它的值为正数或0,所以|a|的最小值为0,而-|a|一定是非正数,即它的值为负数或0,所以-|a|有最大值0,根据这个结论完成下列问题:
(1)|a|+1有最____值____;
(2)5-|a|有最____值____;
(3)当a的值为____时,|a-1|+2有最____值____;
(4)若|a-1|+|b+1|=0,则ab=____.
21.
同学们都知道,|5-2|表示5与2之差的绝对值,|5-2|也可以利用数轴理解为:如图1,数轴上5与2这两个数所对的两点之间的距离.试回答:
(1)|-5-2|=
_____,这个算式利用数轴可理解为
_____;
(2)求使|x+5|=7成立的所有整数;
(3)求出使|x+5.3|+|x-2.6|=7.9成立的所有整数;
(4)如图2,在笔直的公路一侧有A、B、C、D四个村庄,且AB=BC=CD,现要在公路上开一家超市,使各村庄到超市的距离和最小,则超市的位置应在哪两个村庄之间,为什么?
22.
已知:x1,x2,...,x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=,则y1=___________.
(2)若y2=+,则y2=___________.
(3)若y3=++,求y3的值.
(4)由以上探究可知,若y2012=++...+,则y2012共有___________个不同的值.
在y2012这些不同的值中,最大的值和最小的值得差等于___________,y2012的这些所有的不同的值的绝对值的和等于___________.
23.
如图,点A从原点O出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,5秒后,两点相距15个单位长度,已知点B的速度是点A的速度的2倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度;并在数轴上标出A、B两点从原点O出发运动5秒时的位置.
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,
①再过几秒,A、B两点重合?
②再过几秒,可以让A、B、O三点中一点是另外两点所成线段的中点?
24.
已知a、b、c、d是有理数,|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,求|b-a|-|d-c|的值.
参考答案
1.B.
2.
C.
3.
A.
4.
A.
5.
C
6.
A.
7.C
8.C
9.
甲队.
10.
-5或2.
11.-2或-8
12.
1.
13.-1/214.
7.
15.
1.
16.
解:(1)∵a的相反数是它本身,
∴a=0,
(2),∵b的绝对值是5,
∴b=5或-5,
(3)a+b=0±5=±5.
17.
解:(1);
(2)∵B、C两点的距离=0-(-1)=1,
∴点A表示的数为:-3-1=-4,点B表示的数为0,点C表示的数为-1,点D表示的数为4-1=2.
(1)在数轴上描出四个点的位置即可;
(2)原点取在B处,相当于将原数减去1,从而计算即可.
18.
解:小明、小亮、小花都说错了,只有小倩是对的.改正如下:
小明说错了,-a的绝对值应该分情况进行讨论;
小亮说错了,a的绝对值等于本身的数除了正数还有0;
小花说错了,a为有理数,-|a|不一定是负数,还可能是0,即-|a|是负数和0.
19.解:设B点表示的数为x,则x±1=2,
解得:x=1或9,
当x=1时,AB=1-(-3)=4;
当x=9时,AB=9-(-3)=12;
即线段AB的长为4或12.
20.
解:(1)∵|a|≥0,
∴|a|+1≥1,
∴|a|+1有最小值1;
(2)∵-|a|≤0,
∴5-|a|≤5,
∴5-|a|有最大值5;
(3)∵|a-1|+2≥2,
∴当a=1时,有最小值2;
(4)根据题意,a-1=0,b+1=0,
解得a=1,b=-1,
所以,ab=1×(-1)=-1.
故答案为:(1)小,1;(2)大,5;(3)1,小,2;(4)-1.
21.
解:(1)∵|5-2|表示5与2之差的绝对值,
∴|-5-2|=7,
|-5-2|也可以利用数轴理解为:如图一,数轴上-5与2这两个数所对的两点之间的距离;
故答案为:7;如图,数轴上-5与2这两个数所对的两点之间的距离;
(2)∵使|x+5|=7成立的所有整数,就是5到数轴上任意一点的距离都等于7的点都符合,
∴如图二所示,使|x+5|=7成立的所有整数有:-2,12.
;
(3)由题意可知使|x+5.3|+|x-2.6|=7.9成立的所有整数有:-4,-3,-2,-1,0,1;
(4)由题意可知,且AB=BC=CD,则有A到BC之间距离较近,D到BC之间的距离也较近,
所以超市的位置应在BC两个村庄之间使得各村庄到超市的距离和最小.
22.
解:(1)x1<0时,y1==-1,
x1>0时,y1==-1,
则y1=±1;
(2)若x1>0,x2>0时,y2=+=2,
x1>0,x2<0时,y2=+=0,
x1<0,x2<0时,y2=+=-2,
综上所述,y2=0或±2;
(3)x1>0,x2>0,x3>0,y3=++=3,
x1>0,x2>0,x3<0,y3=++=1,
x1>0,x2<0,x3<0,y3=++=-1,
x1<0,x2<0,x3<0,y3=++=-3,
综上所述,y3=±1或±3;
(4)由以上探究可知,y2012=+++…+,
则y2012共有
2013个不同的值;
在y2012这些不同的值中,最大的值和最小的值的差等于
2012-(-2012)=4024,
y2012的这些所有的不同的值的绝对值的和等于0.
23.
解:(1)设A的速度是x单位长度/秒,则B的速度为2x单位长度/秒,由题意,得
5(x+2x)=15,
解得:x=1,
∴B的速度为2,
∴A到达的位置为-5,B到达的位置是10,在数轴上的位置如图:
答:A的速度为1;B的速度为2.
(2)①设y秒后,A、B两点重合,由题意,得
2y-y=10-(-5),
y=15.
答:再过15秒,A、B两点重合;
②设z秒后,原点恰好在A、B的正中间,由题意,得
10-2z=z+5,
z=.
答:再过秒时,原点恰好处在点A、点B的正中间.
24.
解:∵|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,
∴|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,
∴①a-b=9,c-d=-16,此时|b-a|-|d-c|=|-9|-|16|=9-16=-7,
②a-b=-9,c-d=16,此时|b-a|-|d-c|=|9|-|-16|=9-16=-7,
综上所述,|b-a|-|d-c|的值为-7.
根据|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,可知|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,然后分两种情况讨论即可.
一.选择题
1.
如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则这条数轴的原点在( )
A.
在点A,B之间
B.
在点B,C之间
C.
在点C,D之间
D.
在点D,E之间
2.在数轴上表示数-1和2020的两点分别为A和B,则A和B两点间的距离为( )
A.2019
B.2020
C.2021
D.2022
3.如图,在数轴上-4,-1的对应点分别是A、B,而A是线段BC的中点,则点C所表示的数是( )
A.
-7
B.
-8
C.
-9
D.
-10
4.
对任意有理数a,在式子1-|a|,|a+1|,|-1|+a,|a|+1中,取值不为0的是( )
A.
|a|+1
B.
1-|a|
C.
|a+1|
D.
|-1|+a
5.
如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2020将与圆周上的哪个数字重合(
)
A.
0
B.
1
C.
2
D.
3
6.
如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点可能是( )
A.M或R
B.N或P
C.M或N
D.P或R
7.
满足|a-b|+ab=1的非负整数(a,b)的个数是( )
A.
1
B.
2
C.
3
D.
4
8.
已知x的取值能使|x-3|+|x+2|取得最小值,则所有中整数有(
)
A.
1个
B.
2个
C.
3个
D.
4个
二.填空题
9.
甲、乙两队进行拔河比赛,标志物先向乙队方向移动了0.2m,又向甲队方向移动了0.5m,相持一会儿,又向乙队方向移动了0.4m,随后又向甲队方向移动了1.3m,在大家的欢呼鼓励中,标志物又向甲队方向移动了0.9m,若规定标志物向某队方向移动2m该队即可获胜,那么获胜的队是____.
10.
在数轴上,A、B是两个定点,A表示1,B表示-4,P到A、B的距离和为7,则P表示的数是____.
11.已知|a|=5,|b|=3,且|a-b|=b-a,那么a+b=_.
12.
设a+b+c=0,abc>0,则的值是______.
13.
已知实数x满足|2x+1|+|2x-5|=6,则x的取值范围是____.
14.
如图表示数轴上四个点的位置关系,且它们表示的数分别为p,q,r,s.若|p-r|=10,|p-s|=12,|q-s|=9,则|q-r|的值
15.
李老师从拉面的制作受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段AB,对折后(点A与B重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段AB上的,均变成,变成1,等).那么在线段AB上(除A,B)的点中,在第二次操作后,恰好被拉到与1重合的点所对应的数之和是____.
三.解答题
16.
读如图提供的信息,回答下列问题.
求:(1)a的值;
(2)b的值;
(3)a与b的和.
17.
点A、B、C、D分别表示-3,-1,0,4.请解答下列问题:
(1)在数轴上描出A、B、C、D四个点.
(2)现在把数轴的原点取在点B处,其余均不变,那么点A、B、C、D分别表示什么数.
18.
小明、小亮、小花、小倩四人是一个学习小组的同学,下面是该小组学习有理数的绝对值时进行的小组讨论:
小明说:“-a的绝对值是它的相反数a”;
小亮说:“如果有理数a的绝对值是它本身,那么a一定是正数”;
小花说:“如果a为有理数,那么-|a|一定是负数”;
小倩说:“你们说得都不对”.
你认为这四位同学中谁说错了?谁说对了?错的该怎样改正?
19.
对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点,沿x轴平移1个单位,得到点P的对应点P′,如图,若点A表示的数是-3,点B′则是通过上述操作后得到的点B的对应点,点B′表示的数是2,试求线段AB的长.
20.
用字母a表示一个有理数,则|a|一定是非负数,也就是它的值为正数或0,所以|a|的最小值为0,而-|a|一定是非正数,即它的值为负数或0,所以-|a|有最大值0,根据这个结论完成下列问题:
(1)|a|+1有最____值____;
(2)5-|a|有最____值____;
(3)当a的值为____时,|a-1|+2有最____值____;
(4)若|a-1|+|b+1|=0,则ab=____.
21.
同学们都知道,|5-2|表示5与2之差的绝对值,|5-2|也可以利用数轴理解为:如图1,数轴上5与2这两个数所对的两点之间的距离.试回答:
(1)|-5-2|=
_____,这个算式利用数轴可理解为
_____;
(2)求使|x+5|=7成立的所有整数;
(3)求出使|x+5.3|+|x-2.6|=7.9成立的所有整数;
(4)如图2,在笔直的公路一侧有A、B、C、D四个村庄,且AB=BC=CD,现要在公路上开一家超市,使各村庄到超市的距离和最小,则超市的位置应在哪两个村庄之间,为什么?
22.
已知:x1,x2,...,x2012都是不等于0的有理数,请你探究以下问题:
(1)若y1=,则y1=___________.
(2)若y2=+,则y2=___________.
(3)若y3=++,求y3的值.
(4)由以上探究可知,若y2012=++...+,则y2012共有___________个不同的值.
在y2012这些不同的值中,最大的值和最小的值得差等于___________,y2012的这些所有的不同的值的绝对值的和等于___________.
23.
如图,点A从原点O出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,5秒后,两点相距15个单位长度,已知点B的速度是点A的速度的2倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度;并在数轴上标出A、B两点从原点O出发运动5秒时的位置.
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,
①再过几秒,A、B两点重合?
②再过几秒,可以让A、B、O三点中一点是另外两点所成线段的中点?
24.
已知a、b、c、d是有理数,|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,求|b-a|-|d-c|的值.
参考答案
1.B.
2.
C.
3.
A.
4.
A.
5.
C
6.
A.
7.C
8.C
9.
甲队.
10.
-5或2.
11.-2或-8
12.
1.
13.-1/2
7.
15.
1.
16.
解:(1)∵a的相反数是它本身,
∴a=0,
(2),∵b的绝对值是5,
∴b=5或-5,
(3)a+b=0±5=±5.
17.
解:(1);
(2)∵B、C两点的距离=0-(-1)=1,
∴点A表示的数为:-3-1=-4,点B表示的数为0,点C表示的数为-1,点D表示的数为4-1=2.
(1)在数轴上描出四个点的位置即可;
(2)原点取在B处,相当于将原数减去1,从而计算即可.
18.
解:小明、小亮、小花都说错了,只有小倩是对的.改正如下:
小明说错了,-a的绝对值应该分情况进行讨论;
小亮说错了,a的绝对值等于本身的数除了正数还有0;
小花说错了,a为有理数,-|a|不一定是负数,还可能是0,即-|a|是负数和0.
19.解:设B点表示的数为x,则x±1=2,
解得:x=1或9,
当x=1时,AB=1-(-3)=4;
当x=9时,AB=9-(-3)=12;
即线段AB的长为4或12.
20.
解:(1)∵|a|≥0,
∴|a|+1≥1,
∴|a|+1有最小值1;
(2)∵-|a|≤0,
∴5-|a|≤5,
∴5-|a|有最大值5;
(3)∵|a-1|+2≥2,
∴当a=1时,有最小值2;
(4)根据题意,a-1=0,b+1=0,
解得a=1,b=-1,
所以,ab=1×(-1)=-1.
故答案为:(1)小,1;(2)大,5;(3)1,小,2;(4)-1.
21.
解:(1)∵|5-2|表示5与2之差的绝对值,
∴|-5-2|=7,
|-5-2|也可以利用数轴理解为:如图一,数轴上-5与2这两个数所对的两点之间的距离;
故答案为:7;如图,数轴上-5与2这两个数所对的两点之间的距离;
(2)∵使|x+5|=7成立的所有整数,就是5到数轴上任意一点的距离都等于7的点都符合,
∴如图二所示,使|x+5|=7成立的所有整数有:-2,12.
;
(3)由题意可知使|x+5.3|+|x-2.6|=7.9成立的所有整数有:-4,-3,-2,-1,0,1;
(4)由题意可知,且AB=BC=CD,则有A到BC之间距离较近,D到BC之间的距离也较近,
所以超市的位置应在BC两个村庄之间使得各村庄到超市的距离和最小.
22.
解:(1)x1<0时,y1==-1,
x1>0时,y1==-1,
则y1=±1;
(2)若x1>0,x2>0时,y2=+=2,
x1>0,x2<0时,y2=+=0,
x1<0,x2<0时,y2=+=-2,
综上所述,y2=0或±2;
(3)x1>0,x2>0,x3>0,y3=++=3,
x1>0,x2>0,x3<0,y3=++=1,
x1>0,x2<0,x3<0,y3=++=-1,
x1<0,x2<0,x3<0,y3=++=-3,
综上所述,y3=±1或±3;
(4)由以上探究可知,y2012=+++…+,
则y2012共有
2013个不同的值;
在y2012这些不同的值中,最大的值和最小的值的差等于
2012-(-2012)=4024,
y2012的这些所有的不同的值的绝对值的和等于0.
23.
解:(1)设A的速度是x单位长度/秒,则B的速度为2x单位长度/秒,由题意,得
5(x+2x)=15,
解得:x=1,
∴B的速度为2,
∴A到达的位置为-5,B到达的位置是10,在数轴上的位置如图:
答:A的速度为1;B的速度为2.
(2)①设y秒后,A、B两点重合,由题意,得
2y-y=10-(-5),
y=15.
答:再过15秒,A、B两点重合;
②设z秒后,原点恰好在A、B的正中间,由题意,得
10-2z=z+5,
z=.
答:再过秒时,原点恰好处在点A、点B的正中间.
24.
解:∵|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,
∴|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,
∴①a-b=9,c-d=-16,此时|b-a|-|d-c|=|-9|-|16|=9-16=-7,
②a-b=-9,c-d=16,此时|b-a|-|d-c|=|9|-|-16|=9-16=-7,
综上所述,|b-a|-|d-c|的值为-7.
根据|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,可知|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,然后分两种情况讨论即可.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
