浙教版九年级上册 第四章 相似三角形 专题练习:相似三角形的性质及应用(1)(word版,含答案)
文档属性
| 名称 | 浙教版九年级上册 第四章 相似三角形 专题练习:相似三角形的性质及应用(1)(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 480.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-04 06:26:04 | ||
图片预览

文档简介
专题:相似三角形的性质与应用
一.选择题
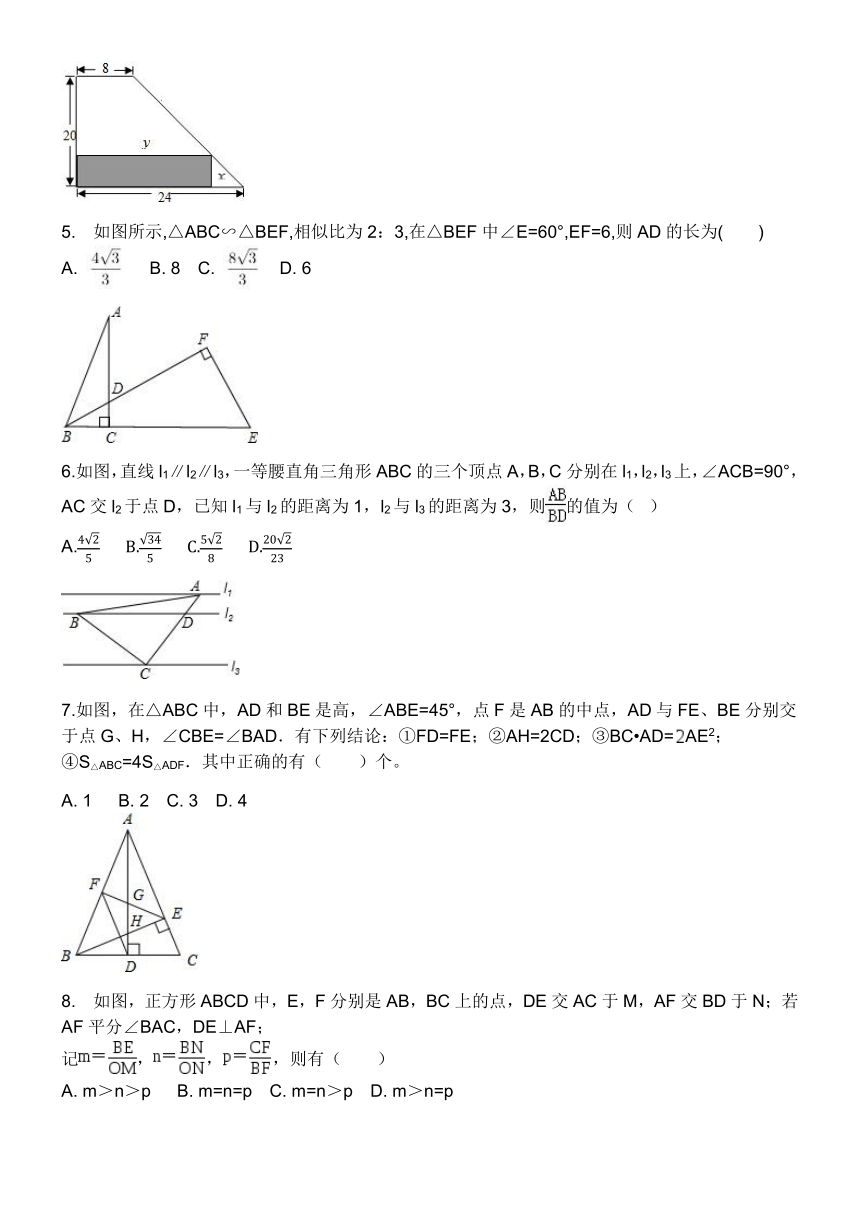
1.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为(
).
A.
2.5
B.2.8
C.3
D.
3.2
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1
,
还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2020次操作后得到的折痕D2019E2019到BC的距离记为h2020;若h1=1,则h2020的值为(
).
A.
B.
C.1-
D.2-
如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是(
)cm.
A.5
B.6
C.(6-)
D.(3+)
4.某厂有许多形状为直角梯形的铁皮边角料,如图.为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x,y应为( )
A.
x=15,y=12
B.
x=12,y=15
C.
x=14,y=10
D.
x=10,y=14
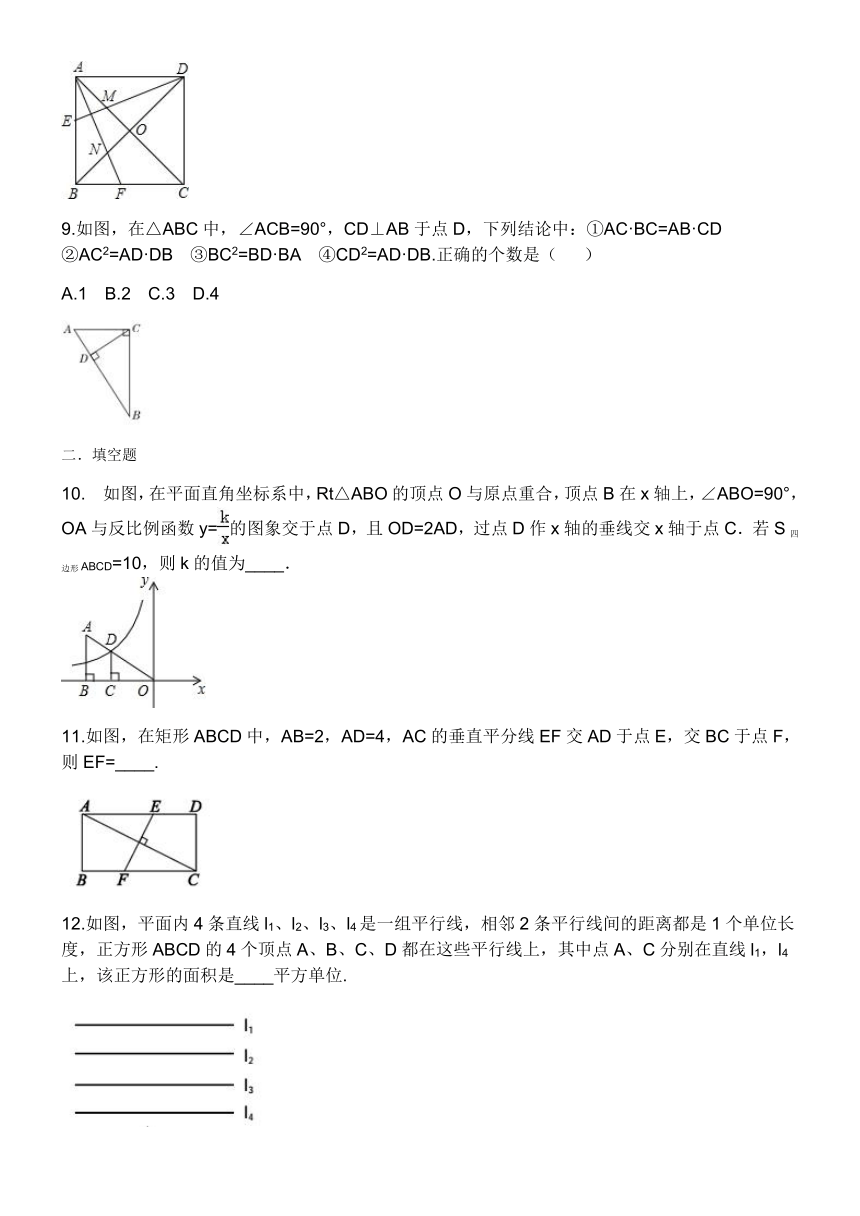
5.
如图所示,△ABC∽△BEF,相似比为2:3,在△BEF中∠E=60°,EF=6,则AD的长为( )
A.
B.
8
C.
D.
6
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则的值为(
?)
A.
B.
C.
D.
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC?AD=AE2;④S△ABC=4S△ADF.其中正确的有( )个。
A.
1
B.
2
C.
3
D.
4
8.
如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于N;若AF平分∠BAC,DE⊥AF;
记,,,则有( )
A.
m>n>p
B.
m=n=p
C.
m=n>p
D.
m>n=p
9.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中:①AC·BC=AB·CD
②AC2=AD·DB
③BC2=BD·BA
④CD2=AD·DB.正确的个数是(
)
A.1
B.2
C.3
D.4
二.填空题
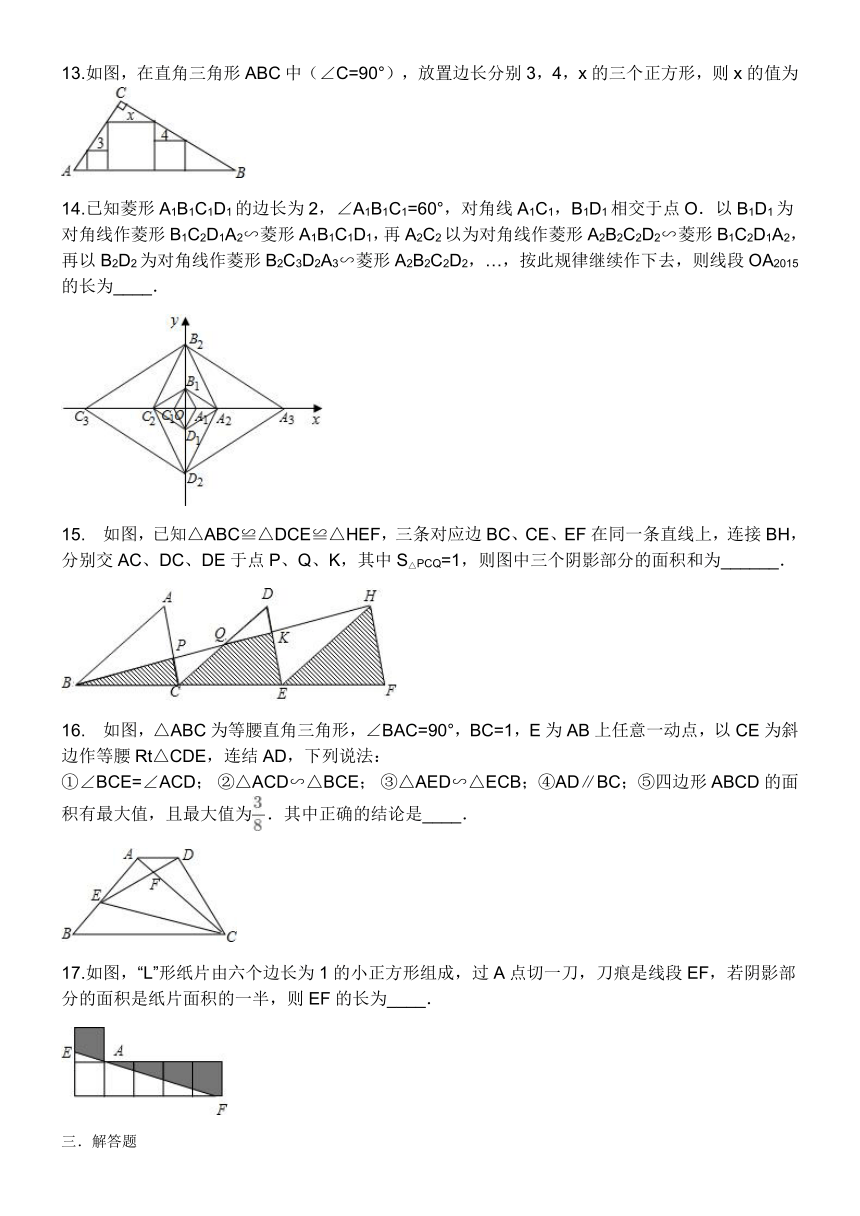
10.
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为____.
11.如图,在矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则EF=____.
12.如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1,l4上,该正方形的面积是____平方单位.
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为
14.已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再A2C2以为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,则线段OA2015的长为____.
15.
如图,已知△ABC≌△DCE≌△HEF,三条对应边BC、CE、EF在同一条直线上,连接BH,分别交AC、DC、DE于点P、Q、K,其中S△PCQ=1,则图中三个阴影部分的面积和为______.
16.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;?②△ACD∽△BCE;?③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为.其中正确的结论是____.
17.如图,“L”形纸片由六个边长为1的小正方形组成,过A点切一刀,刀痕是线段EF,若阴影部分的面积是纸片面积的一半,则EF的长为____.
三.解答题
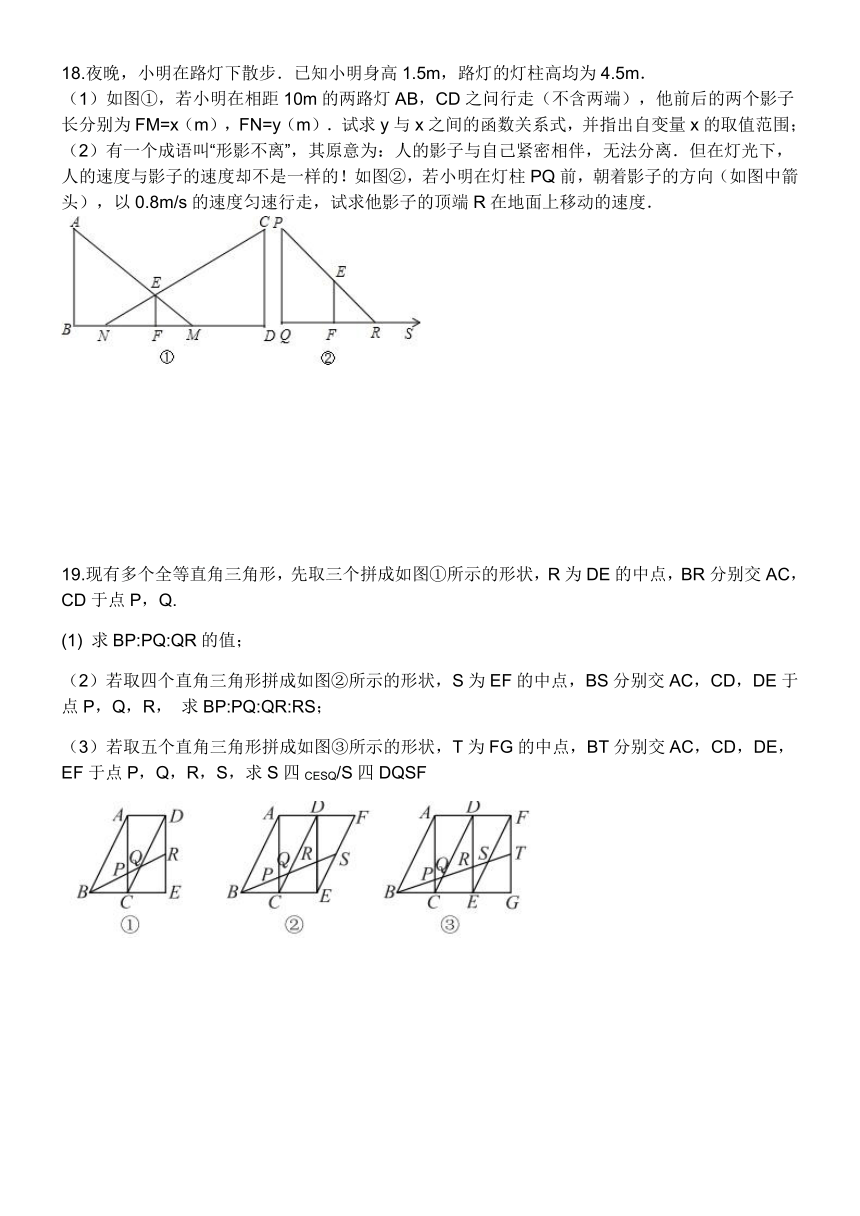
18.夜晚,小明在路灯下散步.已知小明身高1.5m,路灯的灯柱高均为4.5m.
(1)如图①,若小明在相距10m的两路灯AB,CD之问行走(不含两端),他前后的两个影子长分别为FM=x(m),FN=y(m).试求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)有一个成语叫“形影不离”,其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图②,若小明在灯柱PQ前,朝着影子的方向(如图中箭头),以0.8m/s的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
19.现有多个全等直角三角形,先取三个拼成如图①所示的形状,R为DE的中点,BR分别交AC,CD于点P,Q.
(1)
求BP:PQ:QR的值;
(2)若取四个直角三角形拼成如图②所示的形状,S为EF的中点,BS分别交AC,CD,DE于点P,Q,R,
求BP:PQ:QR:RS;
(3)若取五个直角三角形拼成如图③所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于点P,Q,R,S,求S四CESQ/S四DQSF
20.
课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
21.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).
(1)连接DP,经过1秒后,四边形EQDP能够成为平行四边形吗?请说明理由;
(2)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行.为什么?
(3)当t为何值时,△EDQ为直角三角形.
22.
如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE?CB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.
23.
如图,AB是⊙O的直径,C、P是上两点,AB=13,AC=5.
(1)如图(1),若点P是的中点,求PA的长;
(2)如图(2),若点P是的中点,求PA的长.
24.已知:如图,在△ABC中,点D.E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF?BA,CF与DE相交于点G.
(1)求证:DF?AB=BC?DG;
(2)当点E为AC的中点时,求证:.
25.已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在AC上,且∠MPN=90°.
(1)当点P为线段AC的中点,点M、N分别在线段AB、BC上时(如图1),过点P作PE⊥AB于点E,PF⊥BC于点F.证明:△PME∽△PNF,PN=PM.
(2)当PC=PA,点M、N分别在线段AB、BC或其延长线上,如图2、图3这两种情况时,请分别写出线段PN、PM之间的数量关系(不用证明).
26.
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)
当F为BE中点时,求证:AM=CE;
(2)
若
=2,求
的值;
(3)
若
=n,当n为何值时,MN∥BE?
27.
在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
28.
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点
纸片利用率=×100%
发现:
(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
说明:方案三中的每条边均过其中两个正方形的顶点.
参考答案
1.B
2.D
3.B
4.
A
5.
C
6.A.
7.D
8.D
9.C.
10.
﹣16.
11.
.
12.
5或9.
13.
7
14.
32014
15.
13
16.
①②④⑤,
17.
2.
18.解:(1)∵EF∥AB,
∴∠MEF=∠A,∠MFE=∠B.
∴△MEF∽△MAB.
∴===.
∴=,MB=3x?
BF=3x-x=2x.
同理,DF=2y.????
∵BD=10
∴2x+2y=10
∴y=-x+5?????
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
??
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF∥PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴===,
∴=,
∵EE'∥RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴=,
∴=,
∴RR'=1.2t,
∴V影子==1.2米/秒.
19.
解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴∠BCQ=∠BES,∠BQC=∠BSE,
∴△BCQ∽△BES.
又∵BC=CE,
∴CQ=SE=EF,
∴DQ=EF.
∵AB∥CD,
∴∠ABP=∠DQR,∠ACQ=∠BAP.
又∵AC∥DE,
∴∠ACQ=∠QDR,
∴∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
(2)∵五个直角三角形是全等直角三角形
∴AB=CD=EF,AB∥CD∥EF,AC=DE=GF,AC∥DE∥GF,BC=CE=EG,
∴BP=PR=RT,
∵AC∥DE∥GF,
∴△BPC∽△BER∽△BTG,
∴PC=TG=FG,RE=TG=FG,
∴AP=FG,DR=FG,FT=FG
∴AP:DR:FT=5:4:3.
∵AC∥DE∥GF,
∴∠BPA=∠QRD=∠STF.
又∵∠BAP=∠QDR=∠SFT,
∴△BAP∽△QDR∽△SFT.
∴BP:QR:ST=AP:DR:FT=5:4:3.
又∵BP:PR:RT=1:1:1,
∴BP:PQ:QR:RS:ST=5:(5-4):4:(5-3):3=5:1:4:2:3.
20.
解:(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得x=48.
∴加工成的正方形零件的边长是48mm;
(2)如图2,设PQ=x,则PN=2x,AE=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得:x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,mm;
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴=,
即=,
解得:PQ=80-x.
则S=PN?PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
故S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm).
21.
(1)能,
如图1,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以1.25厘米/秒的速度沿BC向终点C运动,t=1秒,
∴AP=1厘米,BQ=1.25厘米,
∵AC=4cm,BC=5cm,点D在BC上,CD=3cm,
∴PC=AC-AP=4-1=3(厘米),QD=BC-BQ-CD=5-1.25-3=0.75(厘米),
∵PE∥BC,
∴△APE∽△ACD,
∴=,=,解得PE=0.75,
∵PE∥BC,PE=QD,
∴四边形EQDP是平行四边形;
(2)如图2,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以1.25厘米/秒的速度沿BC向终点C运动,
∴PC=AC-AP=4-t,QC=BC-BQ=5-1.25t,
∴==1-,==1-,
∴=,
又∵∠C=∠C,
∴△CPQ∽△CAB,
∴∠CPQ=∠CAB,
∴PQ∥AB;
(3)分两种情况讨论:
①如图3,当∠EQD=90°时,显然有EQ=PC=4-t,
又∵EQ∥AC,
∴△EDQ∽△ADC
∴=,
∵BC=5厘米,CD=3厘米,
∴BD=2厘米,
∴DQ=1.25t-2,
∴=,解得t=2.5(秒);
②如图4,当∠QED=90°时,作EM⊥BC于M,CN⊥AD于N,则四边形EMCP是矩形,EM=PC=4-t,
在Rt△ACD中,
∵AC=4厘米,CD=3厘米,
∴AD===5,
∴CN==,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,
∴==,=,解得t=3.1(秒).
综上所述,当t=2.5秒或t=3.1秒时,△EDQ为直角三角形.
22.
证明:(1)∵AC2=CE?CB,
∴.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
(2)∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴
∵点E是BC的中点,
∴CE=BE,
∴
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
23.
解:(1)如图(1)所示,连接PB.
∵AB是⊙O的直径且P是的中点
∴∠PAB=∠PBA=45°,∠APB=90°
∴△APB是等腰直角三角形
∵在等腰直角△APB中,AB=13
∴PA===;
(2)如图(2)所示:连接BC、OP,相交于M点,作PN⊥AB于点N.
∵P点为的中点
∴OP⊥BC,∠OMB=90°
又∵AB为直径
∴∠ACB=90°
∴∠ACB=∠OMB
∴OP∥AC
∴∠CAB=∠POB
又∵∠ACB=∠ONP=90°
∴△ACB∽△ONP
∴
又∵AB=13,AC=5,OP=
代入得ON=
∴AN=OA+ON=9
∴在Rt△OPN中,有NP2=OP2-ON2=36
在Rt△ANP中有PA=
∴PA=.
24.
证明:(1)∵BC2=BF?BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴△BAC∽△BCF,
∵DE∥BC,
∴△BCF∽△DGF,
∴△DGF∽△BAC,
∴DF:BC=DG:BA,
∴DF?AB=BC?DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
∴AH=2EG,
∵AH∥DG,
∴△AHF∽△DGF,
∴=,
∴.
25.【解答】解:(1)如图1,作PF⊥BC,
∵∠ABC=90°,PE⊥AB,
∴PE∥BC,PF∥AB,
∴四边形PFBE是矩形,
∴∠EPF=90°
∴P是AC的中点,
∴PE=BC,PF=AB,
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
∴△MPE∽△NPF,
∴==,
∵∠A=30°,
在RT△ABC中,cot30°==,
∴=,
即PN=PM;
(2)如图2,PN=PM,
如图2?
在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F,
∴四边形BFPE是矩形,
∴△PFN∽△PEM,
∴=,
又∵Rt△AEP和Rt△PFC中,∠A=30°,∠ACB=60°,
∴PF=PC,PE=PA,
∴==,
∵PC=PA?
∴=,
即:PN=PM,
如图3,在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F,
∴四边形BFPE是矩形,
∴△PFN∽△PEM,
∴=,
又∵Rt△AEP和Rt△PFC中,∠A=30°,∠ACB=60°,
∴PF=PC,PE=PA,
∴==,
∵PC=PA?
∴=,
即:PN=PM.
26.
(1)解:当F为BE中点时,如图1,则有BF=EF.
∵四边形ABCD是矩形,∴AB=DC,AB∥DC,∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,∵
,∴△BMF≌△ECF,∴BM=EC.
∵E为CD的中点,∴EC=
DC,∴BM=EC=
DC=
AB,∴AM=BM=EC;
(2)解:如图2所示:设MB=a.
∵四边形ABCD是矩形,∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,∴△ECF∽△BMF,∴
=
=2,∴EC=2a,∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵
=2,∴BC=AD=2a.
∵MN⊥MC,∴∠CMN=90°,∴∠AMN+∠BMC=90°.
∵∠A=90°,∴∠ANM+∠AMN=90°,∴∠BMC=∠ANM,∴△AMN∽△BCM,∴
=
,∴
=
,∴AN=
a,ND=AD﹣AN=2a﹣
a=
a,∴
=
=3;
(3)
解:当
=
=n时,如图3:设MB=a.
∵△MFB∽△CFE,∴
=
,即
,解得:EC=an,∴AB=2an.
又∵
=n,∴
,∴BC=2a.
∵MN∥BE,MN⊥MC,∴∠EFC=∠HMC=90°,∴∠FCB+∠FBC=90°.
∵∠MBC=90°,∴∠BMC+∠FCB=90°,∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,∴△MBC∽△BCE,∴
=
,∴
=
,∴n=4.
27.
(1)证明:∵∠ACP=∠B,∠A=∠A,∴△ACP∽△ABC,,.(2)①解法一:延长PB至点D,使BD=PB,连接CD.∵M为CP的中点,∴CD∥MB.∵∠PBM=∠ACP,∴∠D=∠PBM=∠ACP.∵△ADC∽△ACP,,设BP=x,,解得(舍去负根),即.解法二:取AP的中点E,连接EM.∵M为CP的中点,∴ME∥AC,.∵∠PBM=∠ACP,∴∠PME=∠PBM,∴△EBM∽△EMP,.设BP=x,,解得(舍去负根),即.②.
28.
解:发现:(1)小明的这个发现正确.
理由:
解法一:如图一:连接AC、BC、AB,
∵AC=BC=,AB=2
∴AC2+BC2=AB2,
∴∠BCA=90°,
∴AB为该圆的直径.
解法二:如图二:连接AC、BC、AB.
易证△AMC≌△BNC,
∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,
∴∠BCN+∠ACM=90°,
即∠BCA=90°,
∴AB为该圆的直径.
(2)如图三:∵DE=FH,DE∥FH,
∴∠AED=∠EFH,
∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),
∴AD=EH=1.
∵DE∥BC,
∴△ADE∽△ACB,
∴=,
∴=,
∴BC=8,
∴S△ACB=16.
∴该方案纸片利用率=×100%=×100%=37.5%;
探究:(3)过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,
∵PQ∥EK,
易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴AP:AQ=QK:EK=1:2,
∴AQ=2a,PQ=a,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=a,
则PG=5a+a=a,GL=a,
∴GH=a,
∵,
解得:GB=a,
∴AB=a,AC=a,
∴S△ABC=×AB×AC=a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=×100%=×100%=49.86%.
一.选择题
1.如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为(
).
A.
2.5
B.2.8
C.3
D.
3.2
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1
,
还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2020次操作后得到的折痕D2019E2019到BC的距离记为h2020;若h1=1,则h2020的值为(
).
A.
B.
C.1-
D.2-
如图,一块含30°角的直角三角板,它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是(
)cm.
A.5
B.6
C.(6-)
D.(3+)
4.某厂有许多形状为直角梯形的铁皮边角料,如图.为降低消耗,开源节流,现要从这些边角料上截取矩形铁片(如图中阴影部分)备用,当截取的矩形面积最大时,矩形两边长x,y应为( )
A.
x=15,y=12
B.
x=12,y=15
C.
x=14,y=10
D.
x=10,y=14
5.
如图所示,△ABC∽△BEF,相似比为2:3,在△BEF中∠E=60°,EF=6,则AD的长为( )
A.
B.
8
C.
D.
6
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则的值为(
?)
A.
B.
C.
D.
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC?AD=AE2;④S△ABC=4S△ADF.其中正确的有( )个。
A.
1
B.
2
C.
3
D.
4
8.
如图,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于M,AF交BD于N;若AF平分∠BAC,DE⊥AF;
记,,,则有( )
A.
m>n>p
B.
m=n=p
C.
m=n>p
D.
m>n=p
9.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中:①AC·BC=AB·CD
②AC2=AD·DB
③BC2=BD·BA
④CD2=AD·DB.正确的个数是(
)
A.1
B.2
C.3
D.4
二.填空题
10.
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为____.
11.如图,在矩形ABCD中,AB=2,AD=4,AC的垂直平分线EF交AD于点E,交BC于点F,则EF=____.
12.如图,平面内4条直线l1、l2、l3、l4是一组平行线,相邻2条平行线间的距离都是1个单位长度,正方形ABCD的4个顶点A、B、C、D都在这些平行线上,其中点A、C分别在直线l1,l4上,该正方形的面积是____平方单位.
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为
14.已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再A2C2以为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,则线段OA2015的长为____.
15.
如图,已知△ABC≌△DCE≌△HEF,三条对应边BC、CE、EF在同一条直线上,连接BH,分别交AC、DC、DE于点P、Q、K,其中S△PCQ=1,则图中三个阴影部分的面积和为______.
16.
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连结AD,下列说法:①∠BCE=∠ACD;?②△ACD∽△BCE;?③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为.其中正确的结论是____.
17.如图,“L”形纸片由六个边长为1的小正方形组成,过A点切一刀,刀痕是线段EF,若阴影部分的面积是纸片面积的一半,则EF的长为____.
三.解答题
18.夜晚,小明在路灯下散步.已知小明身高1.5m,路灯的灯柱高均为4.5m.
(1)如图①,若小明在相距10m的两路灯AB,CD之问行走(不含两端),他前后的两个影子长分别为FM=x(m),FN=y(m).试求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)有一个成语叫“形影不离”,其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图②,若小明在灯柱PQ前,朝着影子的方向(如图中箭头),以0.8m/s的速度匀速行走,试求他影子的顶端R在地面上移动的速度.
19.现有多个全等直角三角形,先取三个拼成如图①所示的形状,R为DE的中点,BR分别交AC,CD于点P,Q.
(1)
求BP:PQ:QR的值;
(2)若取四个直角三角形拼成如图②所示的形状,S为EF的中点,BS分别交AC,CD,DE于点P,Q,R,
求BP:PQ:QR:RS;
(3)若取五个直角三角形拼成如图③所示的形状,T为FG的中点,BT分别交AC,CD,DE,EF于点P,Q,R,S,求S四CESQ/S四DQSF
20.
课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
21.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).
(1)连接DP,经过1秒后,四边形EQDP能够成为平行四边形吗?请说明理由;
(2)连接PQ,在运动过程中,不论t取何值时,总有线段PQ与线段AB平行.为什么?
(3)当t为何值时,△EDQ为直角三角形.
22.
如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CE?CB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.
23.
如图,AB是⊙O的直径,C、P是上两点,AB=13,AC=5.
(1)如图(1),若点P是的中点,求PA的长;
(2)如图(2),若点P是的中点,求PA的长.
24.已知:如图,在△ABC中,点D.E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF?BA,CF与DE相交于点G.
(1)求证:DF?AB=BC?DG;
(2)当点E为AC的中点时,求证:.
25.已知在Rt△ABC中,∠ABC=90°,∠A=30°,点P在AC上,且∠MPN=90°.
(1)当点P为线段AC的中点,点M、N分别在线段AB、BC上时(如图1),过点P作PE⊥AB于点E,PF⊥BC于点F.证明:△PME∽△PNF,PN=PM.
(2)当PC=PA,点M、N分别在线段AB、BC或其延长线上,如图2、图3这两种情况时,请分别写出线段PN、PM之间的数量关系(不用证明).
26.
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)
当F为BE中点时,求证:AM=CE;
(2)
若
=2,求
的值;
(3)
若
=n,当n为何值时,MN∥BE?
27.
在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
28.
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点
纸片利用率=×100%
发现:
(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
说明:方案三中的每条边均过其中两个正方形的顶点.
参考答案
1.B
2.D
3.B
4.
A
5.
C
6.A.
7.D
8.D
9.C.
10.
﹣16.
11.
.
12.
5或9.
13.
7
14.
32014
15.
13
16.
①②④⑤,
17.
2.
18.解:(1)∵EF∥AB,
∴∠MEF=∠A,∠MFE=∠B.
∴△MEF∽△MAB.
∴===.
∴=,MB=3x?
BF=3x-x=2x.
同理,DF=2y.????
∵BD=10
∴2x+2y=10
∴y=-x+5?????
∵当EF接近AB时,影长FM接近0;
当EF接近CD时,影长FM接近5
∴0<x<5;
??
(2)如图,设运动时间为t秒,则EE'=FF'=0.8t
∵EF∥PQ
∴∠REF=∠RPQ,∠RFE=∠RQP
∴△REF∽△RPQ
∴===,
∴=,
∵EE'∥RR'
∴∠PEE'=∠PRR',∠PE'E=∠PR'R
∴△PEE'∽△PRR'
∴=,
∴=,
∴RR'=1.2t,
∴V影子==1.2米/秒.
19.
解:(1)∵四个直角三角形是全等三角形,
∴AB=EF=CD,AB∥EF∥CD,BC=CE,AC∥DE,
∴BP:PR=BC:CE=1,
∵CD∥EF,
∴∠BCQ=∠BES,∠BQC=∠BSE,
∴△BCQ∽△BES.
又∵BC=CE,
∴CQ=SE=EF,
∴DQ=EF.
∵AB∥CD,
∴∠ABP=∠DQR,∠ACQ=∠BAP.
又∵AC∥DE,
∴∠ACQ=∠QDR,
∴∠BAP=∠QDR,
∴△BAP∽△QDR.
∴BP:QR=4:3.
∴BP:PQ:QR=4:1:3,
∵DQ∥SE,
∴QR:RS=DQ:SE=3:2,
∴BP:PQ:QR:RS=4:1:3:2.
(2)∵五个直角三角形是全等直角三角形
∴AB=CD=EF,AB∥CD∥EF,AC=DE=GF,AC∥DE∥GF,BC=CE=EG,
∴BP=PR=RT,
∵AC∥DE∥GF,
∴△BPC∽△BER∽△BTG,
∴PC=TG=FG,RE=TG=FG,
∴AP=FG,DR=FG,FT=FG
∴AP:DR:FT=5:4:3.
∵AC∥DE∥GF,
∴∠BPA=∠QRD=∠STF.
又∵∠BAP=∠QDR=∠SFT,
∴△BAP∽△QDR∽△SFT.
∴BP:QR:ST=AP:DR:FT=5:4:3.
又∵BP:PR:RT=1:1:1,
∴BP:PQ:QR:RS:ST=5:(5-4):4:(5-3):3=5:1:4:2:3.
20.
解:(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,
∴AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得x=48.
∴加工成的正方形零件的边长是48mm;
(2)如图2,设PQ=x,则PN=2x,AE=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴=,即=,
解得:x=,
∴2x=,
∴这个矩形零件的两条边长分别为mm,mm;
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴=,
即=,
解得:PQ=80-x.
则S=PN?PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
故S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm).
21.
(1)能,
如图1,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以1.25厘米/秒的速度沿BC向终点C运动,t=1秒,
∴AP=1厘米,BQ=1.25厘米,
∵AC=4cm,BC=5cm,点D在BC上,CD=3cm,
∴PC=AC-AP=4-1=3(厘米),QD=BC-BQ-CD=5-1.25-3=0.75(厘米),
∵PE∥BC,
∴△APE∽△ACD,
∴=,=,解得PE=0.75,
∵PE∥BC,PE=QD,
∴四边形EQDP是平行四边形;
(2)如图2,∵点P以1厘米/秒的速度沿AC向终点C运动,点Q以1.25厘米/秒的速度沿BC向终点C运动,
∴PC=AC-AP=4-t,QC=BC-BQ=5-1.25t,
∴==1-,==1-,
∴=,
又∵∠C=∠C,
∴△CPQ∽△CAB,
∴∠CPQ=∠CAB,
∴PQ∥AB;
(3)分两种情况讨论:
①如图3,当∠EQD=90°时,显然有EQ=PC=4-t,
又∵EQ∥AC,
∴△EDQ∽△ADC
∴=,
∵BC=5厘米,CD=3厘米,
∴BD=2厘米,
∴DQ=1.25t-2,
∴=,解得t=2.5(秒);
②如图4,当∠QED=90°时,作EM⊥BC于M,CN⊥AD于N,则四边形EMCP是矩形,EM=PC=4-t,
在Rt△ACD中,
∵AC=4厘米,CD=3厘米,
∴AD===5,
∴CN==,
∵∠CDA=∠EDQ,∠QED=∠C=90°,
∴△EDQ∽△CDA,
∴==,=,解得t=3.1(秒).
综上所述,当t=2.5秒或t=3.1秒时,△EDQ为直角三角形.
22.
证明:(1)∵AC2=CE?CB,
∴.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
(2)∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴
∵点E是BC的中点,
∴CE=BE,
∴
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.
23.
解:(1)如图(1)所示,连接PB.
∵AB是⊙O的直径且P是的中点
∴∠PAB=∠PBA=45°,∠APB=90°
∴△APB是等腰直角三角形
∵在等腰直角△APB中,AB=13
∴PA===;
(2)如图(2)所示:连接BC、OP,相交于M点,作PN⊥AB于点N.
∵P点为的中点
∴OP⊥BC,∠OMB=90°
又∵AB为直径
∴∠ACB=90°
∴∠ACB=∠OMB
∴OP∥AC
∴∠CAB=∠POB
又∵∠ACB=∠ONP=90°
∴△ACB∽△ONP
∴
又∵AB=13,AC=5,OP=
代入得ON=
∴AN=OA+ON=9
∴在Rt△OPN中,有NP2=OP2-ON2=36
在Rt△ANP中有PA=
∴PA=.
24.
证明:(1)∵BC2=BF?BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴△BAC∽△BCF,
∵DE∥BC,
∴△BCF∽△DGF,
∴△DGF∽△BAC,
∴DF:BC=DG:BA,
∴DF?AB=BC?DG;
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
∴AH=2EG,
∵AH∥DG,
∴△AHF∽△DGF,
∴=,
∴.
25.【解答】解:(1)如图1,作PF⊥BC,
∵∠ABC=90°,PE⊥AB,
∴PE∥BC,PF∥AB,
∴四边形PFBE是矩形,
∴∠EPF=90°
∴P是AC的中点,
∴PE=BC,PF=AB,
∵∠MPN=90°,∠EPF=90°,
∴∠MPE=∠NPF,
∴△MPE∽△NPF,
∴==,
∵∠A=30°,
在RT△ABC中,cot30°==,
∴=,
即PN=PM;
(2)如图2,PN=PM,
如图2?
在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F,
∴四边形BFPE是矩形,
∴△PFN∽△PEM,
∴=,
又∵Rt△AEP和Rt△PFC中,∠A=30°,∠ACB=60°,
∴PF=PC,PE=PA,
∴==,
∵PC=PA?
∴=,
即:PN=PM,
如图3,在Rt△ABC中,过点P作PE⊥AB于E,PF⊥BC于点F,
∴四边形BFPE是矩形,
∴△PFN∽△PEM,
∴=,
又∵Rt△AEP和Rt△PFC中,∠A=30°,∠ACB=60°,
∴PF=PC,PE=PA,
∴==,
∵PC=PA?
∴=,
即:PN=PM.
26.
(1)解:当F为BE中点时,如图1,则有BF=EF.
∵四边形ABCD是矩形,∴AB=DC,AB∥DC,∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,∵
,∴△BMF≌△ECF,∴BM=EC.
∵E为CD的中点,∴EC=
DC,∴BM=EC=
DC=
AB,∴AM=BM=EC;
(2)解:如图2所示:设MB=a.
∵四边形ABCD是矩形,∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,∴△ECF∽△BMF,∴
=
=2,∴EC=2a,∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵
=2,∴BC=AD=2a.
∵MN⊥MC,∴∠CMN=90°,∴∠AMN+∠BMC=90°.
∵∠A=90°,∴∠ANM+∠AMN=90°,∴∠BMC=∠ANM,∴△AMN∽△BCM,∴
=
,∴
=
,∴AN=
a,ND=AD﹣AN=2a﹣
a=
a,∴
=
=3;
(3)
解:当
=
=n时,如图3:设MB=a.
∵△MFB∽△CFE,∴
=
,即
,解得:EC=an,∴AB=2an.
又∵
=n,∴
,∴BC=2a.
∵MN∥BE,MN⊥MC,∴∠EFC=∠HMC=90°,∴∠FCB+∠FBC=90°.
∵∠MBC=90°,∴∠BMC+∠FCB=90°,∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,∴△MBC∽△BCE,∴
=
,∴
=
,∴n=4.
27.
(1)证明:∵∠ACP=∠B,∠A=∠A,∴△ACP∽△ABC,,.(2)①解法一:延长PB至点D,使BD=PB,连接CD.∵M为CP的中点,∴CD∥MB.∵∠PBM=∠ACP,∴∠D=∠PBM=∠ACP.∵△ADC∽△ACP,,设BP=x,,解得(舍去负根),即.解法二:取AP的中点E,连接EM.∵M为CP的中点,∴ME∥AC,.∵∠PBM=∠ACP,∴∠PME=∠PBM,∴△EBM∽△EMP,.设BP=x,,解得(舍去负根),即.②.
28.
解:发现:(1)小明的这个发现正确.
理由:
解法一:如图一:连接AC、BC、AB,
∵AC=BC=,AB=2
∴AC2+BC2=AB2,
∴∠BCA=90°,
∴AB为该圆的直径.
解法二:如图二:连接AC、BC、AB.
易证△AMC≌△BNC,
∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,
∴∠BCN+∠ACM=90°,
即∠BCA=90°,
∴AB为该圆的直径.
(2)如图三:∵DE=FH,DE∥FH,
∴∠AED=∠EFH,
∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),
∴AD=EH=1.
∵DE∥BC,
∴△ADE∽△ACB,
∴=,
∴=,
∴BC=8,
∴S△ACB=16.
∴该方案纸片利用率=×100%=×100%=37.5%;
探究:(3)过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,
∵PQ∥EK,
易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴AP:AQ=QK:EK=1:2,
∴AQ=2a,PQ=a,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=a,
则PG=5a+a=a,GL=a,
∴GH=a,
∵,
解得:GB=a,
∴AB=a,AC=a,
∴S△ABC=×AB×AC=a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=×100%=×100%=49.86%.
同课章节目录
