2.5直角三角(2)

(共13张PPT)
动动手 试一试
等腰直角三角形斜边上的中线等于斜边的一半
D
∠A=∠B=45°
若Rt△ABC中，∠C=90°,AC=BC ，
则
CD= AB
故：
吗？
若Rt△ABC中，∠C=90°,
AC=BC ，CD⊥AB于D,
则 AD=
AD=BD=CD
反思
A
C
B
D
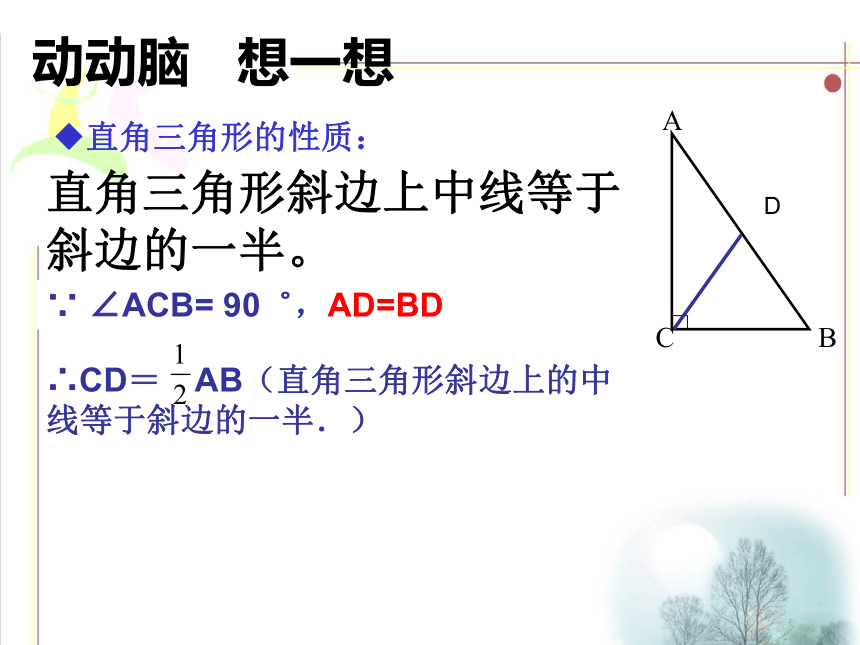
直角三角形的性质：
直角三角形斜边上中线等于斜边的一半。
∵ ∠ACB= 90゜，CD是AB上的中线．
∴CD＝　AB（直角三角形斜边上的中线等于斜边的一半．）
动动脑 想一想
∵ ∠ACB= 90゜，D是AB上的中点．
∵ ∠ACB= 90゜，AD=BD
③若∠A =40°，则其他角为多少度？
④若∠A=30°，你能得到什么结论？
②CD=2cm，则AB的长为多少？
若图中，△ABC是直角三角形，CD是斜边AB上的中线，
①AB=10cm，CD的长为多少cm
A
C
B
D
动动笔 做一做
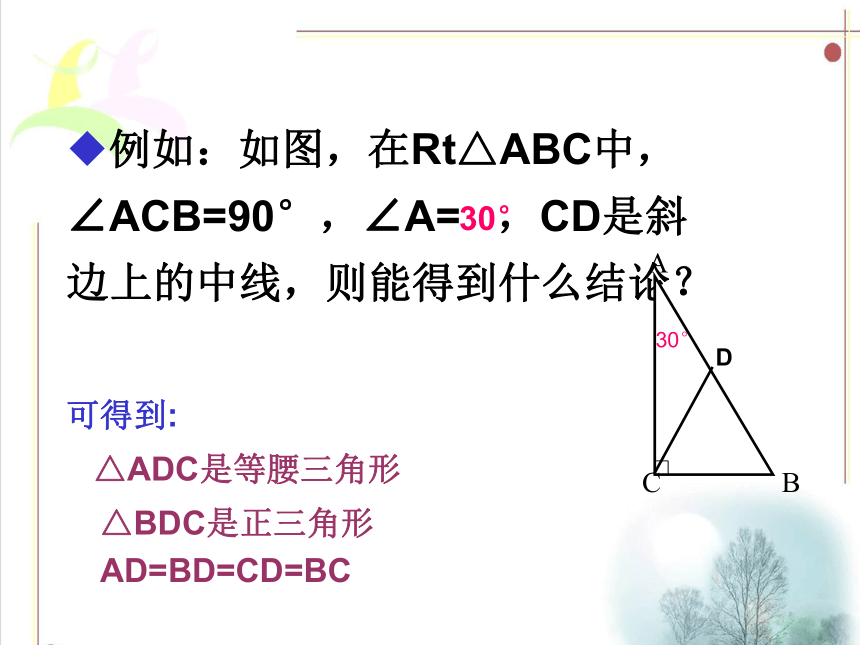
例如：如图，在Rt△ABC中，∠ACB=90°，∠A= ，CD是斜边上的中线，则能得到什么结论？
30°
A
C
B
D
30°
可得到:
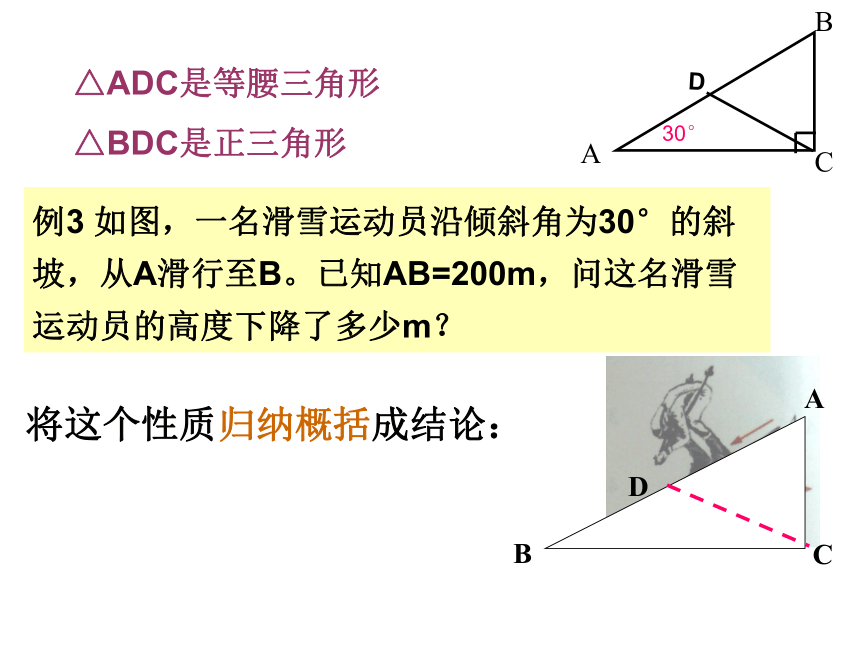
△ADC是等腰三角形
△BDC是正三角形
AD=BD=CD=BC
例3 如图，一名滑雪运动员沿倾斜角为30°的斜坡，从A滑行至B。已知AB=200m，问这名滑雪运动员的高度下降了多少m？
A
B
C
D
将这个性质归纳概括成结论：
A
C
B
D
30°
△ADC是等腰三角形
△BDC是正三角形
在直角三角形中，
30°角所对的直角边等于斜边的一半。
A
B
C
30°
∵△ABC是直角三角形，∠B=30°
∴AC= AB
（在直角三角形中， 30°角所对的直角边等于斜边的一半）
如图是一副三角板拼成的四边形ABCD，E为BD的中点。点E与点A，C的距离相等吗？
A
B
D
E
C
请说明理由。
如图是一副三角板拼成的四边形ABCD，E为AD的中点。点E与点B，C的距离相等吗？请说明理由。
A
B
D
E
C
连结BC，取BC的中点F,你能知道BC与EF的位置关系吗？
F
如图，已知AB⊥BD， AC⊥CD ,E为AD的中点。EB与EC相等吗？请说明理由。
F
如图，已知△ABG中，AB⊥BD于B，AC⊥CD于C ,E为AD的中点，点F是BC的中点,EF垂直BC吗？请说明理由。
G
如图，在△ABC中，CD是AB边上的中线，且CD= AB，△ABC是直角三角形吗？
直角三角形斜边上中线等于斜边的一半。反过来，一个三角形中，若一边上的中线等于这条边的一半，它是直角三角形吗？
A
D
B
C
1
2
若三角形中一边上的中线等于这条边的一半，那么这个三角形是直角三角形。
解：∵CD是中线，CD = AB，
∴AD=CD，CD=BD
∴∠A=∠1，∠B=∠2
∵∠A+∠1+∠B+∠2=180°
∴∠A+∠B=∠1+∠2=90°
∴ △ABC是直角三角形。
动动笔 做一做
1、直角三角形斜边上中线等于斜边的一半。
2、直角三角形中，30°的锐角所对的直角边等于斜边的一半。
动动口 说一说
本节中的知识：
本节中的方法和思想：
1、特殊到一般、一般到特殊、转化(化归思想)
2、观察、归纳、概括
课后思考：
“在直角三角形中，如果一条直角边是斜边的一半，那么这条直角边所对的角是30°”这句话对吗