浙教版数学八年级上册 3.1 不等式的认识 同步习题(word版含答案)
文档属性
| 名称 | 浙教版数学八年级上册 3.1 不等式的认识 同步习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-05 00:00:00 | ||
图片预览

文档简介
浙教版数学八上
3.1
不等式的认识
同步习题及答案
[预习自测]
1.
用
连接的式子叫做不等式。常见的不等式有
。
2.
一般的,一个含有未知数的不等式的
解,组成这个不等式的解的集合,简称
。
[知识点1]
不等式的基本概念
1.
用不等式表示数量的不等关系.
⑴
是正数
⑵
是非负数
⑶
的相反数不大于1
⑷
与的差是负数
⑸
的4倍不小于8
⑹
的相反数与的一半的差不是正数
⑺
的3倍不大于的
⑻
不比0大
2.
用不等式表示:
⑴
的与的差大于;
⑵
的与的和小于;
⑶
的倍与的的差是非负数;
⑷
与的和的不大于.
3.
下列各式中,是不等式的为(
)
A.
B.5x+y>9
C.5x2-7y
D.x+=8
4.判断下列式子哪些是不等式?若不是请说明理由。
(1)2>0
(2)a2+1>0
(3)3x2+2x
(4)x<2x+1
(5)x=2x-5
(6)a+b≠c
[知识点2]
不等式的解集
5.如图,数轴所表示的不等式,正确的是(
)
A.>2
B.<2
C.≥2
D.≤2
[基础练习]
6.
根据下列数量关系列不等式.
①
的一半与3的和比5大.
②
的3倍与1的差不小于2.
③
的与2的差是非负数.
④
与2的和是非正数.
⑤与1的差小于5而不小于3.
⑥的大于的20%与-6的差.
7.(1)已知x1=1,x2=2,请在数轴上表示出x1,x2的位置
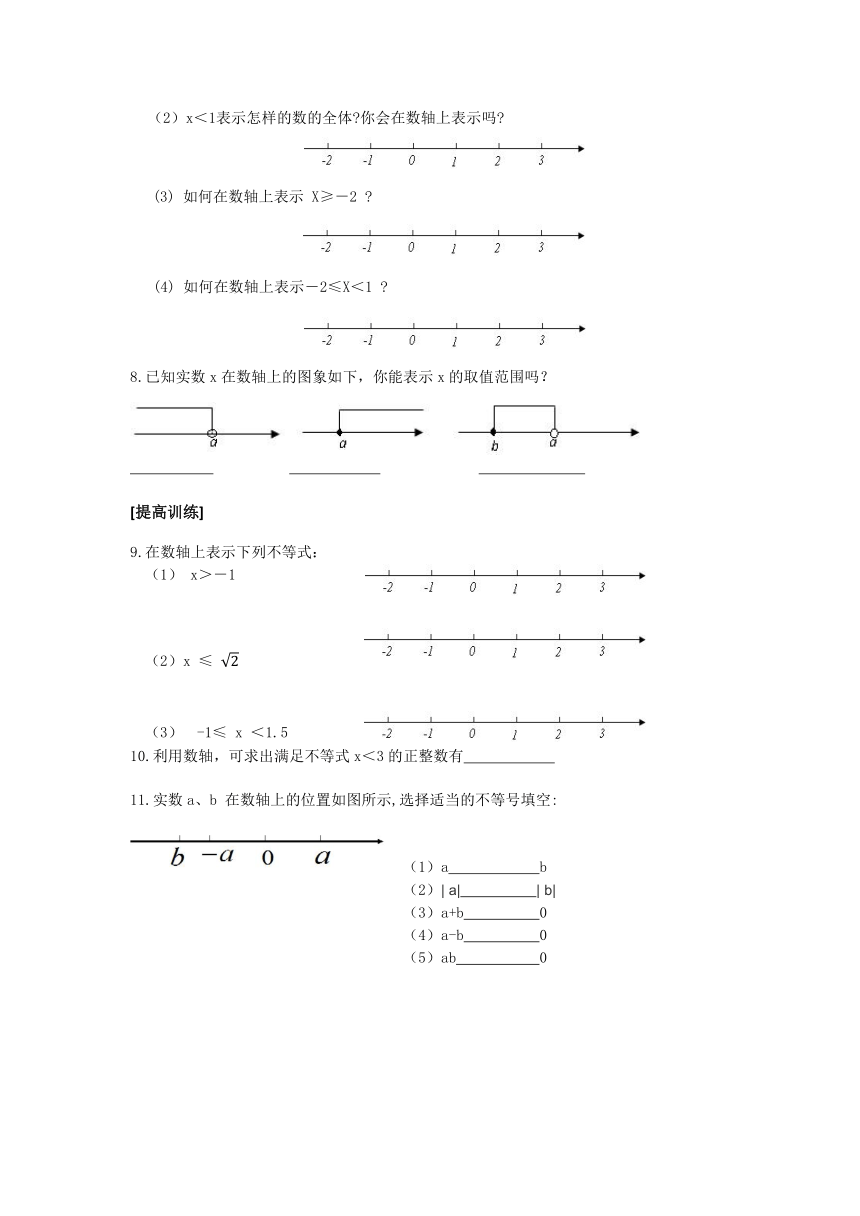
(2)x<1表示怎样的数的全体?你会在数轴上表示吗?
(3)
如何在数轴上表示
X≥-2
?
(4)
如何在数轴上表示-2≤X<1
?
8.已知实数x在数轴上的图象如下,你能表示x的取值范围吗?
[提高训练]
9.在数轴上表示下列不等式:
(1)
x>-1
(2)x
≤
-1≤
x
<1.5
10.利用数轴,可求出满足不等式x<3的正整数有
11.实数a、b
在数轴上的位置如图所示,选择适当的不等号填空:
(1)a
b
(2)|
a|
|
b|
(3)a+b
0
(4)a-b
0
(5)ab
0
参考答案
[预习自测]
1.
不等号
<,>,≥,≤,≠
2.
所有
不等式的解集
[知识点1]
不等式的基本概念
1.
⑴
>0
⑵
≥0
⑶
-a
≤1
⑷
x-y<0
⑸
4m≥8
⑹
-q-q≤0
⑺
3x≤x
⑻
a≤0
2.
⑴
x-6>2
⑵
y+4⑶
3a-
b≥0
⑷
30%(x+5)≤-2
3.
B
4.(1)
(2)
(4)
(6)
[知识点2]
不等式的解集
5.A
[基础练习]
6.
①
a+3>5
②
3x-1≤2
③x-2≥0
④
m+2≤0
⑤3≤x-1<5
⑥a>20%a-(-6)
7.(1)
(2)
(3)
(4)
8.
xx≥a
b≤x[提高训练]
9.
10.
1,2
11.
(1)>
(2)<
(3)<
(4)>
(5)<
3.1
不等式的认识
同步习题及答案
[预习自测]
1.
用
连接的式子叫做不等式。常见的不等式有
。
2.
一般的,一个含有未知数的不等式的
解,组成这个不等式的解的集合,简称
。
[知识点1]
不等式的基本概念
1.
用不等式表示数量的不等关系.
⑴
是正数
⑵
是非负数
⑶
的相反数不大于1
⑷
与的差是负数
⑸
的4倍不小于8
⑹
的相反数与的一半的差不是正数
⑺
的3倍不大于的
⑻
不比0大
2.
用不等式表示:
⑴
的与的差大于;
⑵
的与的和小于;
⑶
的倍与的的差是非负数;
⑷
与的和的不大于.
3.
下列各式中,是不等式的为(
)
A.
B.5x+y>9
C.5x2-7y
D.x+=8
4.判断下列式子哪些是不等式?若不是请说明理由。
(1)2>0
(2)a2+1>0
(3)3x2+2x
(4)x<2x+1
(5)x=2x-5
(6)a+b≠c
[知识点2]
不等式的解集
5.如图,数轴所表示的不等式,正确的是(
)
A.>2
B.<2
C.≥2
D.≤2
[基础练习]
6.
根据下列数量关系列不等式.
①
的一半与3的和比5大.
②
的3倍与1的差不小于2.
③
的与2的差是非负数.
④
与2的和是非正数.
⑤与1的差小于5而不小于3.
⑥的大于的20%与-6的差.
7.(1)已知x1=1,x2=2,请在数轴上表示出x1,x2的位置
(2)x<1表示怎样的数的全体?你会在数轴上表示吗?
(3)
如何在数轴上表示
X≥-2
?
(4)
如何在数轴上表示-2≤X<1
?
8.已知实数x在数轴上的图象如下,你能表示x的取值范围吗?
[提高训练]
9.在数轴上表示下列不等式:
(1)
x>-1
(2)x
≤
-1≤
x
<1.5
10.利用数轴,可求出满足不等式x<3的正整数有
11.实数a、b
在数轴上的位置如图所示,选择适当的不等号填空:
(1)a
b
(2)|
a|
|
b|
(3)a+b
0
(4)a-b
0
(5)ab
0
参考答案
[预习自测]
1.
不等号
<,>,≥,≤,≠
2.
所有
不等式的解集
[知识点1]
不等式的基本概念
1.
⑴
>0
⑵
≥0
⑶
-a
≤1
⑷
x-y<0
⑸
4m≥8
⑹
-q-q≤0
⑺
3x≤x
⑻
a≤0
2.
⑴
x-6>2
⑵
y+4
3a-
b≥0
⑷
30%(x+5)≤-2
3.
B
4.(1)
(2)
(4)
(6)
[知识点2]
不等式的解集
5.A
[基础练习]
6.
①
a+3>5
②
3x-1≤2
③x-2≥0
④
m+2≤0
⑤3≤x-1<5
⑥a>20%a-(-6)
7.(1)
(2)
(3)
(4)
8.
x
b≤x
9.
10.
1,2
11.
(1)>
(2)<
(3)<
(4)>
(5)<
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
