第3章 圆的基本性质单元测试卷(含解析)
文档属性
| 名称 | 第3章 圆的基本性质单元测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 695.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级上册数学
圆的基本性质
单元测试卷
(满分120分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列说法中,正确的是(
)
A.
同一条弦所对的两条弧一定是等弧
B.
长度相等的两条弧是等弧
C.
弦的中垂线一定经过圆心
D.
三角形的外心到三角形各边的距离相等
已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( )
A.
①②③
B.
①②④
C.
①②⑤
D.
①②③⑤
如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )
???????
A.
100米
B.
110米
C.
120米
D.
200米
如图,在⊙O中,弦AB、CD相交于点E,∠A=50°,∠B=30°,则∠BED的大小为( )
A.
80°
B.
100°
C.
110°
D.
105°
如图,用圆心角为120°,半径为6
cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的底面周长是(
)
A.
2π
cm
B.
3π
cm
C.
4π
cm
D.
5π
cm
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,且∠BAC=120°,BC=2.若在这个圆面上随意抛飞镖,则飞镖落在扇形ABC内的概率是( )
A.
B.
C.
D.
点P(5,-3)绕着原点顺时针旋转90°的点的坐标是( )
A.
(-3,5)
B.
(-3,-5)
C.
(3,5)
D.
(3,-5)
如图,MN是的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点若,则的最小值是(??
??).
A.
B.
C.
1
D.
2
如图,AB是⊙O的直径,AB=8,弦CD垂直平分OB,E是弧AD上的动点,AF⊥CE于点F,点E在弧AD上从A运动到D的过程中,线段CF扫过的面积为( )
A.
4π+3
B.
4π+
C.
π+
D.
π+3
如图1所示,小明(点)在操场上跑步,操场由两段半圆形弯道和两段直道构成,若小明从点(右侧弯道起点)出发以顺时针方向沿着跑道行进.设行进的路程为x,小明到右侧半圆形弯道的圆心的距离为,可绘制出如图2所示函数图象,那么的值应为(
)
A.
4
B.
C.
D.
二、填空题(本大题共10小题,共30.0分)
正方形是中心对称图形,它绕它的中心旋转一周和原来的图形重合_______次.
矩形ABCD中,边AB=6cm,AD=8cm.若作⊙A,使B、C、D三点至少有一个点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是
____________.????????
如图将△ABC
绕点B
顺时针旋转
50°,点C
的对应点C′落在AB
的延长线上,则∠A′BC=________.
在半径为5cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为2cm,则油槽面宽AB=______cm.
已知A是⊙O上的一个动点,P是⊙O所在平面内的一个定点.若PA的最大值为9,最小值为3,则⊙O的半径为?
?
?
?
?。
如图,7根圆柱形木棒的横截面圆的半径均为1,则捆扎这7根木棒一周的绳子长度为______
.
如图,在矩形ABCD
中,AB=2,BC=,以点B
为圆心,AB
为半径画弧,交AC于点E,交BC
于点F,则图中阴影部分的面积为?
?
?
?
??。
?
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,那么∠B的度数为?
?
?
?
?。
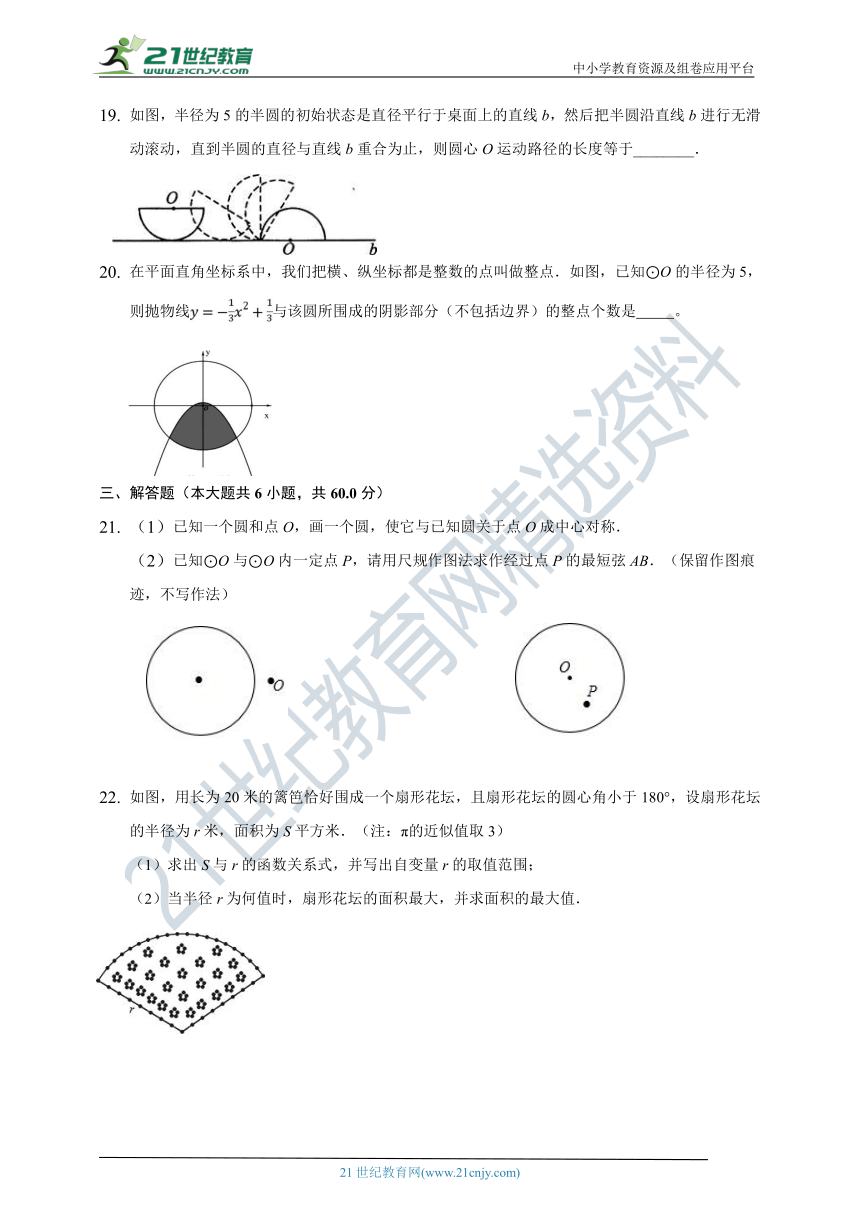
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,直到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于________.
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线与该圆所围成的阴影部分(不包括边界)的整点个数是?
?
?
?。
三、解答题(本大题共6小题,共60.0分)
(1)已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
(2)已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
(1)求出S与r的函数关系式,并写出自变量r的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B.
(1)求证:AC=BD;
(2)若OA=2,∠A=30°,当AC⊥BD时,求弧CD的长.
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.
(1)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积.
P是以AB为直径的半圆上一动点(P与A、B不重合),O为圆心,CO⊥AP,OC、BC与AP分别相交于D、E两点,AB=12.
(1)若∠ABC=35°,求∠PAB的度数;
(2)若AP平分线段BC,求弦AP的长度;
(3)是否存在点P,使△PBC的面积为整数,如果存在,这样的P点有几个?(直接写出结果,不需写出解题过程.)
如图,在平面直角坐标系中,抛物线y=a(x+1)(x﹣3)(a为常数,且a≠0)与x轴交于A、B两点,与y轴交于点D,以AB为直径的⊙M恰好经过点D,且与y轴负半轴交于点C,P是劣弧BC上一动点.
?
(1)求⊙M的半径及a的值;
(2)如图1,Q为弧PC的中点,弦AP、DQ交于点G,连接AD,求证:AD=AG;
(3)如图2,连接PA、PB、PC、PD,求代数式的值.
答案和解析
【答案】C
【解析】本题考查了圆心角、弧、弦的关系,垂径定理以及三角形的外接圆与外心:熟练掌握与圆有关的概念和性质定理是解题的关键。
2.【答案】B
【解析】连接AD,AB是直径,则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;
∵∠ABE=90°-∠EBC-∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确.
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误
故选:B.
3.【答案】A
【解析】∵每次小明都是沿直线前进10米后向左转36°,
∴他走过的图形是正多边形,每个外角都为36°,
∴边数n=360°÷36°=10,
∴他第一次回到出发点A时,一共走了10×10=100米.
本题考查了正多边形的边数的求法,根据题意判断出小亮走过的图形是正多边形是解题的关键.
4.【答案】B
【解析】由圆周角定理推知∠A=∠D=50°,再根据三角形内角和定理求得即可.
5.【答案】C
【解析】这个纸帽的底面周长==4π(cm).
利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,用弧长公式计算即可.
6.【答案】C
【解析】如图,连接AO,∠BAC=120°,根据等腰三角形的性质得到AO⊥BC,∠BAO=60°,解直角三角形得到AB=,由扇形的面积公式得到扇形ABC的面积==,根据概率公式即可得到结论.
本题考查了几何概率,扇形的面积的计算,等腰三角形的性质,正确的识别图形是解题的关键.
7.【答案】B
【解析】如图,设点P(5,-3)绕着原点顺时针旋转90°得到点P′.
作PM⊥x轴于点M,作P′N⊥y轴于点N.
∴∠POP′=90°,OP′=OP.
在△OPM与△OP′N中,
,
∴△OPM≌△OP′N,
∴P′N=PM=3,ON=OM=5,
∴点P′的坐标为(-3,-5).
本题考查了旋转的性质,全等三角形的判定与性质,正确确定旋转角,证明△OPM≌△OP′N是解决本题的关键.
8.【答案】D
【解析】本题结合图形的性质,考查轴对称--最短路线问题,等腰直角三角形的判定及性质,垂径定理,圆心角、弧、弦的关系,圆周角定理的有关知识,其中求出∠BON的度数是解题的关键.本题是要在MN上找一点P,使PA+PB的值最小,设是A关于MN的对称点,连接,与MN的交点即为点P.此时PA+PB=是最小值,可证是等腰直角三角形,从而得出结果.
9.【答案】A
【解析】连AC,OC,BC.线段CF扫过的面积=扇形MAH的面积+△MCH的面积.证明∠AMH=120°即可解决问题.CF扫过的面积为π×(2)2+?(2)2=4π+3.
本题考查扇形的面积,三角形的面积,线段的垂直平分线的性质,圆周角定理等知识,解题的关键是学会添加常用辅助线面构造特殊三角形解决问题,属于中考常考题型.
10.【答案】D
【解析】此题考查了动点函数图像,根据题意可知,a代表离O最远,b代表离O最近,根据画图可求出a-b的值.
画图如下:
∵b=,
∴点P所在位置最远,是半圆+圆+(a-b)=
∴a-b=--=.
11.【答案】4
【解析】本题考查中心对称的性质。正方形绕中心至少旋转90度后能和原来的图案互相重合.故旋转一周和原来的图形重合4次。
12.【答案】6<r<10
【解析】本题主要考查点与圆的位置关系,矩形的性质有关知识,先根据矩形的性质求出对角线的长度,再根据点与圆的位置关系可得半径r的取值范围.
13.【答案】80
【解析】本题考查了旋转的性质和平角的定义的知识,熟练掌握这些知识是解题的关键,利用旋转的性质得∠ABA'=∠CBC'=50°再通过平角的定义可得∠A'BC=80°
14.【答案】8
【解析】连接OA,过O作OD⊥AB于D,交⊙O于D,
∴AB=2AD,OD=OA-2=3,
在Rt△AOD中,OA2=AD2+OD2,
∴AD=4,∴AB=8,
此题考查了勾股定理的应用和垂径定理的应用,圆中的有关半径,弦长,弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题.
15.【答案】3或6
【解析】若点P在圆外,则⊙O的直径为9-3=6,所以⊙O的半径为3;
若点P在圆内,则⊙O的直径为9+3=12,所以⊙O的半径为6;
综上,⊙O的半径为3或6;
本题主要考查点与圆的位置关系,解题的关键是掌握点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外?d>r
②点P在圆上?d=r
③点P在圆内?d<r.
16.【答案】2π+12
【解析】从图中可以看出,捆扎这7根木棒一周的绳子长度为六段公切线长和六段弧长
根据公切线的定义可知:每条公切线=1+1=2
连接六个圆的圆心的线段正好组成了一个正六边形,
根据正六边形的内角定义可知:
每个内角=180×(6-2)÷6=120°,
故可求出六段弧的圆心角都是360°-90°-90°-120°=60°,
根据弧长公式可得:六段弧长==2π,
故捆扎这7根木棒一周的绳子长度=2π+12.
本题的关键是作图,并从图中可以看出,捆扎这7根木棒一周的绳子长度为六段公切线长和六段弧长,然后根据公式计算.
17.【答案】???????
【解析】本题考查矩形的性质,扇形面积计算,三角形面积计算,解题的关键是构建阴影部分面积的等量关系,连接BE,作于H,作于G,由已知得,BA=BE=BF=2,是等边三角形,,,EG
=,?.
18.【答案】18°
【解析】连接DE,
∵过D、A、C三点的圆的圆心为E,
∴∠C+∠AED=180°,
∵过B、E、F三点的圆的圆心为D,
∴∠BED=∠B=θ,∴∠AED=180°-θ,
∴∠C=90°+θ,
∵∠A+∠C+∠B=180°,
∴63°+90°+θ+θ=180°,解得:θ=18°.
∴∠B=18°.
此题考查了圆周角定理以及三角形内角和定理.此题难度适中,注意掌握辅助线的作法,注意数形结合与方程思想的应用.
19.【答案】5π
【解析】本题考查的是弧长的计算和旋转的知识,解题关键是确定半圆作无滑动翻转所经过的路线并求出长度,属于较难题.
由图形可知,圆心先向前走OO1的长度,从O到O1的运动轨迹是一条直线,长度为圆的周长,然后沿着弧O1O2旋转圆的周长,则圆心O运动路径的长度为:×2π×5+×2π×5=5π
20.【答案】21
【解析】本题考查了二次函数图象上点的坐标特征,注意分类进行,做到不重复不遗漏.
分别找到y=0、y=-1、y=-2、y=-3、y=-4的整点个数,再把它们相加即可求解.
解:当x=0时,代入抛物线方程,得y=;
当x=±1时,代入抛物线方程,得y=0;
当x=±2时,代入抛物线方程,得y=-1;
当x=±3时,代入抛物线方程,得y=;
当x=±4时,代入抛物线方程,得y=-5.
可得y=0的整点个数是1,横坐标为0;
y=-1的整点个数是3,横坐标分别为0和±1;
y=-2的整点个数是5,横坐标分别为0、±1和±2;
y=-3的整点个数是7,横坐标分别为0、±1、±2和±3;
y=-4的整点个数是5,横坐标分别为0、±1和±2.
1+3+5+7+5=21,
∴阴影部分的整数点有21个.
21.【答案】(1)如图,
所以圆O′即为所求.
(2)如图所示:线段AB即为所求;
【解析】本题考查了复杂作图、垂径定理,注意:圆内最长弦为直径,最短的弦为过这点且垂直于这条直径的线.
22.【答案】解:(1)设扇形的弧长为l米.
由题意可知,l+2r=20.∴l=20-2r.
∴.其中4<r<10.
(2)∵S=-r2+10r=-(r-5)2+25.
∴当r=5时,S最大值=25.
【解析】本题主要考查了函数模型的选择与应用.此题涉及中间量转换问题,不过根据公式进行转换难度不是很大.
23.【答案】(1)证明:延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,
∵BE,AF是⊙O的直径,
∴∠EDB=∠FCA=90°.
在△DEB与△CFA中,
∵,
∴△DEB≌△CFA(AAS),
∴AC=BD;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,
∵∠A=30°,OA=OC,
∴∠COA=180°-30°-30°=120°.
∵∠A=∠B=30°,AC⊥BD,
∴∠EOA+∠A=60°,∴∠EOA=30°,
∴∠DOE=60°,∴∠COD=30°,
∴==.
【解析】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
24.【答案】解:(1)PA+PB=PC,理由如下:
如图1,在PC上截取PD=PA,连接AD.由圆周角定理得,∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴△ABC是等边三角形;∴AB=AC,
∵∠APC=60°.PD=PA,
∴△PAD是等边三角形.
∴PA=AD,∠PAD=60°,
∵∠BAC=60°,
∴∠PAB=∠DAC,
在△PAB和△DAC中,,
∴△PAB≌△DAC(SAS)
∴PB=DC,
∵PD+DC=PC,
∴PA+PB=PC;
(2)△ABC是圆内接等边三角形,面积一定,则当点P到AB的距离最大时,△ABP的面积最大,此时点P为的中点,
∴当点P为的中点时,四边形APBC面积最大,
∵CA=CB,∴,
又∵,
∴PC为⊙O的直径,
∴∠PAC=90°,又∠ACP=30°,
∴PA=PC=1,
由勾股定理得,AC==,
∴四边形APBC面积=×1××2=;
∴当P是弧AB中点时,四边形APBC的面积最大为.
【解析】本题考查的是圆周角定理、垂径定理、全等三角形的判定和性质、等边三角形的判定,掌握圆周角定理、全等三角形的判定定理和性质定理是解题的关键.
25.【答案】解:如图连接BP,CP,OP,
(1)∵∠ABC=35°,
∴∠AOC=2∠ABC=70°,
∵CO⊥AP,
∴∠PAB=90°﹣70°=20°;
(2)∵AB是圆的直径,∴BP⊥AP,
∵CO⊥AP,
∴OC∥BP,∠CDE=∠BPE=90°,
∵CE=BE,∠CED=∠BEP,
∴△BPE≌△CDE,
∴CD=BP,
∵AO=BO,OC∥BP,
∴2OD=BP,
∴CD=2OD,
∵OCAB=6,
∴OD=2,BP=4,
由勾股定理可得,AP8;
(3)∵OC∥BP,
∴S△BPC=S△BOP,
∵OB=6,
∴当点P到OB距离为,,,6时,S△BPC为整数,
∴这样的P点有35个.
【解析】此题主要考查圆的综合问题,熟练掌握圆的性质并灵活运用于实际问题的证明,会证明三角形全等,会进行三角形的等积分析是解题的关键.
(1)连接BP,CP,OP,根据圆周角定理和垂径定理进行计算即可;
(2)通过证明三角形全等得出线段CD与OD的关系,进而求出BP,运用勾股定理求解即可;
(3)把S△BPC转化为S△BOP,进而进行分析即可.
26.【答案】解:(1)由已知可知:A(﹣1,0),B(3,0),
∴AB=4,∴⊙M的半径为2,
∵OM=1,DM=2,
∴DO,
∴D(0,),
将点D代入y=a(x+1)(x﹣3),
∴a;
(2)连接AQ、AC、DP,
∵Q为弧PC的中点,
∴∠CDQ=∠PDQ,
∵∠CDA=∠Q,
∴∠DCA+∠CDQ=∠Q+∠QAP,
∴∠AGD=∠ADG,
∴AD=AG;
(3)设P(m,n),
过点P作x轴垂线与x轴交于点T,过点P作y轴垂线交于点H,
在Rt△DHP中,PD2=PH2+DH2,
在Rt△PHC中,PC2=PH2+CH2,
∴PD2﹣PC2=DH2﹣CH2=(DH+CH)(DH﹣CH)=CD?(n﹣n)=2?(﹣2n)=﹣4n,
在Rt△ABP中,AB?PT=PA?PB,∴4(﹣n)=PA?PB,
∴.
???????
【解析】本题考查二次函数的图象与性质,圆的相关性质;熟练掌握二次函数的图象与性质,结合圆、直角三角形的相关知识解题是关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
九年级上册数学
圆的基本性质
单元测试卷
(满分120分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列说法中,正确的是(
)
A.
同一条弦所对的两条弧一定是等弧
B.
长度相等的两条弧是等弧
C.
弦的中垂线一定经过圆心
D.
三角形的外心到三角形各边的距离相等
已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45度.给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧AE是劣弧DE的2倍;⑤AE=BC.其中正确结论的序号是( )
A.
①②③
B.
①②④
C.
①②⑤
D.
①②③⑤
如图,小明从A点出发,沿直线前进10米后向左转36°,再沿直线前进10米,再向左转36°……照这样走下去,他第一次回到出发点A点时,一共走的路程是( )
???????
A.
100米
B.
110米
C.
120米
D.
200米
如图,在⊙O中,弦AB、CD相交于点E,∠A=50°,∠B=30°,则∠BED的大小为( )
A.
80°
B.
100°
C.
110°
D.
105°
如图,用圆心角为120°,半径为6
cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的底面周长是(
)
A.
2π
cm
B.
3π
cm
C.
4π
cm
D.
5π
cm
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,且∠BAC=120°,BC=2.若在这个圆面上随意抛飞镖,则飞镖落在扇形ABC内的概率是( )
A.
B.
C.
D.
点P(5,-3)绕着原点顺时针旋转90°的点的坐标是( )
A.
(-3,5)
B.
(-3,-5)
C.
(3,5)
D.
(3,-5)
如图,MN是的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点若,则的最小值是(??
??).
A.
B.
C.
1
D.
2
如图,AB是⊙O的直径,AB=8,弦CD垂直平分OB,E是弧AD上的动点,AF⊥CE于点F,点E在弧AD上从A运动到D的过程中,线段CF扫过的面积为( )
A.
4π+3
B.
4π+
C.
π+
D.
π+3
如图1所示,小明(点)在操场上跑步,操场由两段半圆形弯道和两段直道构成,若小明从点(右侧弯道起点)出发以顺时针方向沿着跑道行进.设行进的路程为x,小明到右侧半圆形弯道的圆心的距离为,可绘制出如图2所示函数图象,那么的值应为(
)
A.
4
B.
C.
D.
二、填空题(本大题共10小题,共30.0分)
正方形是中心对称图形,它绕它的中心旋转一周和原来的图形重合_______次.
矩形ABCD中,边AB=6cm,AD=8cm.若作⊙A,使B、C、D三点至少有一个点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是
____________.????????
如图将△ABC
绕点B
顺时针旋转
50°,点C
的对应点C′落在AB
的延长线上,则∠A′BC=________.
在半径为5cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度为2cm,则油槽面宽AB=______cm.
已知A是⊙O上的一个动点,P是⊙O所在平面内的一个定点.若PA的最大值为9,最小值为3,则⊙O的半径为?
?
?
?
?。
如图,7根圆柱形木棒的横截面圆的半径均为1,则捆扎这7根木棒一周的绳子长度为______
.
如图,在矩形ABCD
中,AB=2,BC=,以点B
为圆心,AB
为半径画弧,交AC于点E,交BC
于点F,则图中阴影部分的面积为?
?
?
?
??。
?
如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,那么∠B的度数为?
?
?
?
?。
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,直到半圆的直径与直线b重合为止,则圆心O运动路径的长度等于________.
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线与该圆所围成的阴影部分(不包括边界)的整点个数是?
?
?
?。
三、解答题(本大题共6小题,共60.0分)
(1)已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.
(2)已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
(1)求出S与r的函数关系式,并写出自变量r的取值范围;
(2)当半径r为何值时,扇形花坛的面积最大,并求面积的最大值.
如图,在⊙O中,弦AC,BD相交于点M,且∠A=∠B.
(1)求证:AC=BD;
(2)若OA=2,∠A=30°,当AC⊥BD时,求弧CD的长.
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.
(1)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积.
P是以AB为直径的半圆上一动点(P与A、B不重合),O为圆心,CO⊥AP,OC、BC与AP分别相交于D、E两点,AB=12.
(1)若∠ABC=35°,求∠PAB的度数;
(2)若AP平分线段BC,求弦AP的长度;
(3)是否存在点P,使△PBC的面积为整数,如果存在,这样的P点有几个?(直接写出结果,不需写出解题过程.)
如图,在平面直角坐标系中,抛物线y=a(x+1)(x﹣3)(a为常数,且a≠0)与x轴交于A、B两点,与y轴交于点D,以AB为直径的⊙M恰好经过点D,且与y轴负半轴交于点C,P是劣弧BC上一动点.
?
(1)求⊙M的半径及a的值;
(2)如图1,Q为弧PC的中点,弦AP、DQ交于点G,连接AD,求证:AD=AG;
(3)如图2,连接PA、PB、PC、PD,求代数式的值.
答案和解析
【答案】C
【解析】本题考查了圆心角、弧、弦的关系,垂径定理以及三角形的外接圆与外心:熟练掌握与圆有关的概念和性质定理是解题的关键。
2.【答案】B
【解析】连接AD,AB是直径,则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;
∵∠ABE=90°-∠EBC-∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确.
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误
故选:B.
3.【答案】A
【解析】∵每次小明都是沿直线前进10米后向左转36°,
∴他走过的图形是正多边形,每个外角都为36°,
∴边数n=360°÷36°=10,
∴他第一次回到出发点A时,一共走了10×10=100米.
本题考查了正多边形的边数的求法,根据题意判断出小亮走过的图形是正多边形是解题的关键.
4.【答案】B
【解析】由圆周角定理推知∠A=∠D=50°,再根据三角形内角和定理求得即可.
5.【答案】C
【解析】这个纸帽的底面周长==4π(cm).
利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,用弧长公式计算即可.
6.【答案】C
【解析】如图,连接AO,∠BAC=120°,根据等腰三角形的性质得到AO⊥BC,∠BAO=60°,解直角三角形得到AB=,由扇形的面积公式得到扇形ABC的面积==,根据概率公式即可得到结论.
本题考查了几何概率,扇形的面积的计算,等腰三角形的性质,正确的识别图形是解题的关键.
7.【答案】B
【解析】如图,设点P(5,-3)绕着原点顺时针旋转90°得到点P′.
作PM⊥x轴于点M,作P′N⊥y轴于点N.
∴∠POP′=90°,OP′=OP.
在△OPM与△OP′N中,
,
∴△OPM≌△OP′N,
∴P′N=PM=3,ON=OM=5,
∴点P′的坐标为(-3,-5).
本题考查了旋转的性质,全等三角形的判定与性质,正确确定旋转角,证明△OPM≌△OP′N是解决本题的关键.
8.【答案】D
【解析】本题结合图形的性质,考查轴对称--最短路线问题,等腰直角三角形的判定及性质,垂径定理,圆心角、弧、弦的关系,圆周角定理的有关知识,其中求出∠BON的度数是解题的关键.本题是要在MN上找一点P,使PA+PB的值最小,设是A关于MN的对称点,连接,与MN的交点即为点P.此时PA+PB=是最小值,可证是等腰直角三角形,从而得出结果.
9.【答案】A
【解析】连AC,OC,BC.线段CF扫过的面积=扇形MAH的面积+△MCH的面积.证明∠AMH=120°即可解决问题.CF扫过的面积为π×(2)2+?(2)2=4π+3.
本题考查扇形的面积,三角形的面积,线段的垂直平分线的性质,圆周角定理等知识,解题的关键是学会添加常用辅助线面构造特殊三角形解决问题,属于中考常考题型.
10.【答案】D
【解析】此题考查了动点函数图像,根据题意可知,a代表离O最远,b代表离O最近,根据画图可求出a-b的值.
画图如下:
∵b=,
∴点P所在位置最远,是半圆+圆+(a-b)=
∴a-b=--=.
11.【答案】4
【解析】本题考查中心对称的性质。正方形绕中心至少旋转90度后能和原来的图案互相重合.故旋转一周和原来的图形重合4次。
12.【答案】6<r<10
【解析】本题主要考查点与圆的位置关系,矩形的性质有关知识,先根据矩形的性质求出对角线的长度,再根据点与圆的位置关系可得半径r的取值范围.
13.【答案】80
【解析】本题考查了旋转的性质和平角的定义的知识,熟练掌握这些知识是解题的关键,利用旋转的性质得∠ABA'=∠CBC'=50°再通过平角的定义可得∠A'BC=80°
14.【答案】8
【解析】连接OA,过O作OD⊥AB于D,交⊙O于D,
∴AB=2AD,OD=OA-2=3,
在Rt△AOD中,OA2=AD2+OD2,
∴AD=4,∴AB=8,
此题考查了勾股定理的应用和垂径定理的应用,圆中的有关半径,弦长,弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题.
15.【答案】3或6
【解析】若点P在圆外,则⊙O的直径为9-3=6,所以⊙O的半径为3;
若点P在圆内,则⊙O的直径为9+3=12,所以⊙O的半径为6;
综上,⊙O的半径为3或6;
本题主要考查点与圆的位置关系,解题的关键是掌握点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:
①点P在圆外?d>r
②点P在圆上?d=r
③点P在圆内?d<r.
16.【答案】2π+12
【解析】从图中可以看出,捆扎这7根木棒一周的绳子长度为六段公切线长和六段弧长
根据公切线的定义可知:每条公切线=1+1=2
连接六个圆的圆心的线段正好组成了一个正六边形,
根据正六边形的内角定义可知:
每个内角=180×(6-2)÷6=120°,
故可求出六段弧的圆心角都是360°-90°-90°-120°=60°,
根据弧长公式可得:六段弧长==2π,
故捆扎这7根木棒一周的绳子长度=2π+12.
本题的关键是作图,并从图中可以看出,捆扎这7根木棒一周的绳子长度为六段公切线长和六段弧长,然后根据公式计算.
17.【答案】???????
【解析】本题考查矩形的性质,扇形面积计算,三角形面积计算,解题的关键是构建阴影部分面积的等量关系,连接BE,作于H,作于G,由已知得,BA=BE=BF=2,是等边三角形,,,EG
=,?.
18.【答案】18°
【解析】连接DE,
∵过D、A、C三点的圆的圆心为E,
∴∠C+∠AED=180°,
∵过B、E、F三点的圆的圆心为D,
∴∠BED=∠B=θ,∴∠AED=180°-θ,
∴∠C=90°+θ,
∵∠A+∠C+∠B=180°,
∴63°+90°+θ+θ=180°,解得:θ=18°.
∴∠B=18°.
此题考查了圆周角定理以及三角形内角和定理.此题难度适中,注意掌握辅助线的作法,注意数形结合与方程思想的应用.
19.【答案】5π
【解析】本题考查的是弧长的计算和旋转的知识,解题关键是确定半圆作无滑动翻转所经过的路线并求出长度,属于较难题.
由图形可知,圆心先向前走OO1的长度,从O到O1的运动轨迹是一条直线,长度为圆的周长,然后沿着弧O1O2旋转圆的周长,则圆心O运动路径的长度为:×2π×5+×2π×5=5π
20.【答案】21
【解析】本题考查了二次函数图象上点的坐标特征,注意分类进行,做到不重复不遗漏.
分别找到y=0、y=-1、y=-2、y=-3、y=-4的整点个数,再把它们相加即可求解.
解:当x=0时,代入抛物线方程,得y=;
当x=±1时,代入抛物线方程,得y=0;
当x=±2时,代入抛物线方程,得y=-1;
当x=±3时,代入抛物线方程,得y=;
当x=±4时,代入抛物线方程,得y=-5.
可得y=0的整点个数是1,横坐标为0;
y=-1的整点个数是3,横坐标分别为0和±1;
y=-2的整点个数是5,横坐标分别为0、±1和±2;
y=-3的整点个数是7,横坐标分别为0、±1、±2和±3;
y=-4的整点个数是5,横坐标分别为0、±1和±2.
1+3+5+7+5=21,
∴阴影部分的整数点有21个.
21.【答案】(1)如图,
所以圆O′即为所求.
(2)如图所示:线段AB即为所求;
【解析】本题考查了复杂作图、垂径定理,注意:圆内最长弦为直径,最短的弦为过这点且垂直于这条直径的线.
22.【答案】解:(1)设扇形的弧长为l米.
由题意可知,l+2r=20.∴l=20-2r.
∴.其中4<r<10.
(2)∵S=-r2+10r=-(r-5)2+25.
∴当r=5时,S最大值=25.
【解析】本题主要考查了函数模型的选择与应用.此题涉及中间量转换问题,不过根据公式进行转换难度不是很大.
23.【答案】(1)证明:延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,
∵BE,AF是⊙O的直径,
∴∠EDB=∠FCA=90°.
在△DEB与△CFA中,
∵,
∴△DEB≌△CFA(AAS),
∴AC=BD;
(2)延长AO交⊙O于点F,连接CF,延长BO交⊙O于点E,连接DE,CD,OD,OC,
∵∠A=30°,OA=OC,
∴∠COA=180°-30°-30°=120°.
∵∠A=∠B=30°,AC⊥BD,
∴∠EOA+∠A=60°,∴∠EOA=30°,
∴∠DOE=60°,∴∠COD=30°,
∴==.
【解析】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
24.【答案】解:(1)PA+PB=PC,理由如下:
如图1,在PC上截取PD=PA,连接AD.由圆周角定理得,∠ABC=∠APC=60°,∠BAC=∠CPB=60°,
∴△ABC是等边三角形;∴AB=AC,
∵∠APC=60°.PD=PA,
∴△PAD是等边三角形.
∴PA=AD,∠PAD=60°,
∵∠BAC=60°,
∴∠PAB=∠DAC,
在△PAB和△DAC中,,
∴△PAB≌△DAC(SAS)
∴PB=DC,
∵PD+DC=PC,
∴PA+PB=PC;
(2)△ABC是圆内接等边三角形,面积一定,则当点P到AB的距离最大时,△ABP的面积最大,此时点P为的中点,
∴当点P为的中点时,四边形APBC面积最大,
∵CA=CB,∴,
又∵,
∴PC为⊙O的直径,
∴∠PAC=90°,又∠ACP=30°,
∴PA=PC=1,
由勾股定理得,AC==,
∴四边形APBC面积=×1××2=;
∴当P是弧AB中点时,四边形APBC的面积最大为.
【解析】本题考查的是圆周角定理、垂径定理、全等三角形的判定和性质、等边三角形的判定,掌握圆周角定理、全等三角形的判定定理和性质定理是解题的关键.
25.【答案】解:如图连接BP,CP,OP,
(1)∵∠ABC=35°,
∴∠AOC=2∠ABC=70°,
∵CO⊥AP,
∴∠PAB=90°﹣70°=20°;
(2)∵AB是圆的直径,∴BP⊥AP,
∵CO⊥AP,
∴OC∥BP,∠CDE=∠BPE=90°,
∵CE=BE,∠CED=∠BEP,
∴△BPE≌△CDE,
∴CD=BP,
∵AO=BO,OC∥BP,
∴2OD=BP,
∴CD=2OD,
∵OCAB=6,
∴OD=2,BP=4,
由勾股定理可得,AP8;
(3)∵OC∥BP,
∴S△BPC=S△BOP,
∵OB=6,
∴当点P到OB距离为,,,6时,S△BPC为整数,
∴这样的P点有35个.
【解析】此题主要考查圆的综合问题,熟练掌握圆的性质并灵活运用于实际问题的证明,会证明三角形全等,会进行三角形的等积分析是解题的关键.
(1)连接BP,CP,OP,根据圆周角定理和垂径定理进行计算即可;
(2)通过证明三角形全等得出线段CD与OD的关系,进而求出BP,运用勾股定理求解即可;
(3)把S△BPC转化为S△BOP,进而进行分析即可.
26.【答案】解:(1)由已知可知:A(﹣1,0),B(3,0),
∴AB=4,∴⊙M的半径为2,
∵OM=1,DM=2,
∴DO,
∴D(0,),
将点D代入y=a(x+1)(x﹣3),
∴a;
(2)连接AQ、AC、DP,
∵Q为弧PC的中点,
∴∠CDQ=∠PDQ,
∵∠CDA=∠Q,
∴∠DCA+∠CDQ=∠Q+∠QAP,
∴∠AGD=∠ADG,
∴AD=AG;
(3)设P(m,n),
过点P作x轴垂线与x轴交于点T,过点P作y轴垂线交于点H,
在Rt△DHP中,PD2=PH2+DH2,
在Rt△PHC中,PC2=PH2+CH2,
∴PD2﹣PC2=DH2﹣CH2=(DH+CH)(DH﹣CH)=CD?(n﹣n)=2?(﹣2n)=﹣4n,
在Rt△ABP中,AB?PT=PA?PB,∴4(﹣n)=PA?PB,
∴.
???????
【解析】本题考查二次函数的图象与性质,圆的相关性质;熟练掌握二次函数的图象与性质,结合圆、直角三角形的相关知识解题是关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
