2.6 探索勾股定理(2)

(共16张PPT)
（二）
复习旧知
1、勾股定理适用于什么三角形？
2、请根据右图叙述勾股定理
3、若已知Rt△ABC中任意两边长，如何求第三边长？
若知道Rt△ABC的一条边长，以及另外两边长的关系（倍数、比值等），如何求这两边的长？
A
B
C
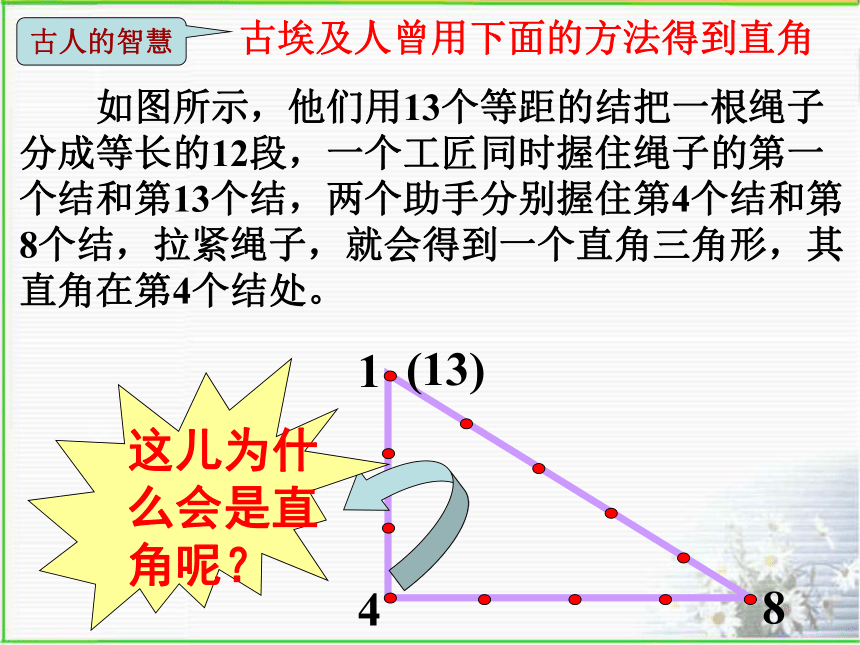
古埃及人曾用下面的方法得到直角
　　如图所示，他们用13个等距的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第一个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，其直角在第4个结处。
1
4
8
(13)
这儿为什么会是直角呢？
古人的智慧
探究一：做一做
一、画一个三角形,使其三边长（a＜b＜c）分别为:
（1）5cm, 12cm, 13cm；（2） 3cm, 4cm, 5cm ；
（3）8cm, 15cm, 17cm；
二、这三组数都满足
吗？
三、再用量角器量一量最大的角，判断它们是否是直角三角形？
由此你得到怎样的结论
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
即如果三角形的三边长a，b，c满足
那么这个三角形是直角三角形.
1.想一想:上述哪条边所对的角是直角
2.能够成为直角三角形三边长的三个正整数，称为勾股数。
如3、4、5；　6、8、10；　5、12、13。
实验论证
A
B
C
D
小明想要检测雕塑底座正面的 AD 边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
小明量得AD长是30厘米,AB长是40厘米, BD长是50厘米，AD边垂直于AB边吗 为什么？
例1 根据下列条件，分别判断以a,b,c为边的三角形是不是直角三角形
（1）a＝7，b＝24，c＝25
（2）a＝1，b＝2，c＝3
小结：已知三边长，判定三角形是否直角三
角形的步骤：
1、找（找最长边）
2、算（短边的平方和是否等于最长边的平方）
1、根据下列条件，判断下面以a、b、
　c 为边的三角形是不是直角三角形
(1)　a=1，b=5/3，c=4/3
(2)　a=5，b=7，c=8
(3)
大显身手
是
是
否
例2、已知△ABC三条边长分别为a,b,c,且a＝m2－n2，b＝2mn，c＝m2＋n2(m>n，m,n是正整数)。△ABC是直角三角形吗？请说明理由.
解：∵ a=m2－n2，b=2mn，c＝m2＋n2
∴a2+b2=(m2－n2)2+(2mn)2
＝m4－2m2n2＋n4＋4m2n2
＝(m2＋n2)2
＝m4＋2m2n2＋n4
＝c2
∴△ABC是直角三角形
2、如图在△ABC中AB=4,BC=2,BD=1,CD=
判断下列结论是否正确，并说明理由
(1) CD ⊥AB; (2) AC⊥BC
D
A
C
B
解(1)∵BC2=BD2 +CD2=4
(2)∵AC2=AD2+CD2=12
∴∠CDB=90°
∴CD⊥AB
AC2+BC2=16=AB2
∴∠ACB=90°
∴AC⊥BC
3、如图，四边形ABCD中，AB＝3，BC=4,CD=12,AD=13, ∠B=90°，求四边形ABCD的面积
┐
D
B
A
C
归纳小结
勾股定理
直角三角形两直角边的平方和等于斜边的平方．
a
c
b
A
B
C
(1)
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
直角三角形的判定方法之一：
因为
所以∠ACB=90°
因为∠ACB=90°
所以
1、 有一块田地的形状和尺寸如图所示，试求它的面积。
∟
∟
A
B
C
D
5
2、 有一块田地的形状和尺寸如图所示，∠B=∠D=90°, ∠A=60°,AB=5米，AD＝4米，试求它的面积。
∟
A
B
C
D
5
∟
4
3、如图，分别以三角形三边向外作正方形、正三角形、半圆。若S1+S2=S3成立，则三角形是Rt△吗？
S1
S2
S3
S1
S2
S3
S1
S2
S3
4、在△ABC中，∠ACB=90度，AC=BC，P是△ABC内一点，且PA=6，PB=2，PC=4，求∠BPC的度数。
C
A
B
P