浙教版八年级数学下册 6.1 反比例函数课件(共16张PPT)
文档属性
| 名称 | 浙教版八年级数学下册 6.1 反比例函数课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 966.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-09 09:15:31 | ||
图片预览






文档简介
(共16张PPT)
6.1反比例函数
画一个面积为6的矩形,有几种不同的画法?
课前热身:
为什么?
x
1
1.5
2
3
4
......
y
矩形的面积为6,一边为x,另一边为y,请完成下表:
观察以上表格,你能得出哪些结论?
y随着x的增大而减小
乘积都为6
y与x成反比例
若两个变量的乘积为一个不为0的常数,我们就这两个变量成反比例关系
思考并回答下面的问题:
1.北京到温州铁路线长为1600km,一列火车从北京开往温州记火车全程的
行驶时间为x(h),火车行驶的平均速度为y(km/h)
,你能完成下表吗?并思考y与x有什么数量关系?能用一个函数表达式表示吗?
x(h)
5
6
12
20
y(km/h)
100
2.小明用20元钱去买同一种菜,买这种菜的数量y(千克)与
单价x(元)之间的关系是
用函数表达式为
观察以上函数表达式,它们有什么共同点?
1.两个变量成反比例关系
2.都可以写成
,
,
特征:
你能参考正比例函数的定义,给反比例函数下一个定义吗?
形如
y=kx(k为常数,k
≠0)
的函数叫正比例函数
形如y=
(k为常数,k
的函数叫正比例函数
≠0)
思考:1.为什么
2.正比例函数与反比例函数有什么相同点和不同点?
k叫作比例系数
k叫作比例系数
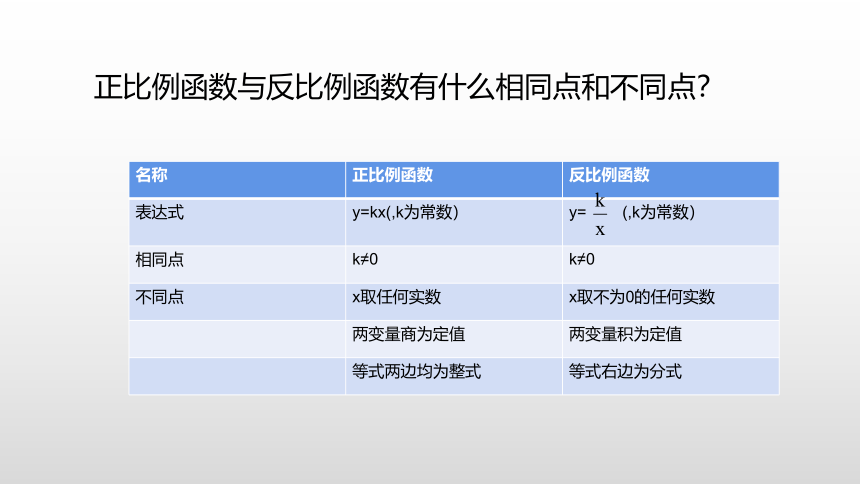
正比例函数与反比例函数有什么相同点和不同点?
名称
正比例函数
反比例函数
表达式
y=kx(,k为常数)
y=
(,k为常数)
相同点
k≠0
k≠0
不同点
x取任何实数
x取不为0的任何实数
两变量商为定值
两变量积为定值
等式两边均为整式
等式右边为分式
练一练
下列函数中,哪些是反比例函数,并指出其比列系数与自变量
取值范围
例题1
当m取何值时,
为反比例函数?
当m取何值时,
为反比例函数?
当m取何值时,
为反比例函数?
练一练
给我一个支点,我可以撬起整个地球
阿基米德:
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力臂
动力
背景知识
杠杆原理
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数;
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
x=500时呢?
x=d时,函数的值?
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
如果把动力臂缩小到原来的
,所需动力将怎样变化?
课堂小结
你觉得本节课有哪些收获?
课后思考:
小学时,我们说:如果y与x成反比例,则y随着x的
增大而减小。
你觉得这个命题现在还成立吗?
6.1反比例函数
画一个面积为6的矩形,有几种不同的画法?
课前热身:
为什么?
x
1
1.5
2
3
4
......
y
矩形的面积为6,一边为x,另一边为y,请完成下表:
观察以上表格,你能得出哪些结论?
y随着x的增大而减小
乘积都为6
y与x成反比例
若两个变量的乘积为一个不为0的常数,我们就这两个变量成反比例关系
思考并回答下面的问题:
1.北京到温州铁路线长为1600km,一列火车从北京开往温州记火车全程的
行驶时间为x(h),火车行驶的平均速度为y(km/h)
,你能完成下表吗?并思考y与x有什么数量关系?能用一个函数表达式表示吗?
x(h)
5
6
12
20
y(km/h)
100
2.小明用20元钱去买同一种菜,买这种菜的数量y(千克)与
单价x(元)之间的关系是
用函数表达式为
观察以上函数表达式,它们有什么共同点?
1.两个变量成反比例关系
2.都可以写成
,
,
特征:
你能参考正比例函数的定义,给反比例函数下一个定义吗?
形如
y=kx(k为常数,k
≠0)
的函数叫正比例函数
形如y=
(k为常数,k
的函数叫正比例函数
≠0)
思考:1.为什么
2.正比例函数与反比例函数有什么相同点和不同点?
k叫作比例系数
k叫作比例系数
正比例函数与反比例函数有什么相同点和不同点?
名称
正比例函数
反比例函数
表达式
y=kx(,k为常数)
y=
(,k为常数)
相同点
k≠0
k≠0
不同点
x取任何实数
x取不为0的任何实数
两变量商为定值
两变量积为定值
等式两边均为整式
等式右边为分式
练一练
下列函数中,哪些是反比例函数,并指出其比列系数与自变量
取值范围
例题1
当m取何值时,
为反比例函数?
当m取何值时,
为反比例函数?
当m取何值时,
为反比例函数?
练一练
给我一个支点,我可以撬起整个地球
阿基米德:
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力臂
动力
背景知识
杠杆原理
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数;
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
x=500时呢?
x=d时,函数的值?
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
如果把动力臂缩小到原来的
,所需动力将怎样变化?
课堂小结
你觉得本节课有哪些收获?
课后思考:
小学时,我们说:如果y与x成反比例,则y随着x的
增大而减小。
你觉得这个命题现在还成立吗?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
