第4章 相似三角形单元测试卷(含解析)
文档属性
| 名称 | 第4章 相似三角形单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 891.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 14:28:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
九年级上册数学
相似三角形
单元测试卷
(满分120分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列各组中的四条线段成比例的是( )
A.
a=2,b=3,c=4,d=1
B.
a=2,b=4,c=3,d=6
C.
a=4,b=6,c=5,d=10
D.
a=1,b=2,c=3,d=4
如图,DE∥AB,下列比例式中不成立的是( )
A.
B.
=
C.
=
D.
=
若x:y=1:3,2y=3z,则的值是(
)
A.
-5
B.
-
C.
D.
5
如图,在△ABC中,∠A=75°,AB=6,AC=8,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
A.B.C.D.
如图,两个三角形是以点P为位似中心的位似图形,则点P的坐标是(
)
A.
(﹣3,2)
B.
(﹣3,1)
C.
(2,﹣3)
D.
(﹣2,3)
如图,在△ABC中,BC=9,∠ABC的平分线BF交AC于点F,点D、点E分别是边AB、AC上的点,若,则BD-DE的值为( )
A.
3
B.
3.5
C.
4
D.
4.5
如图,一张等腰三角形纸片,底边长12
cm,底边上的高为12
cm,现沿底边依次向下往上裁剪宽度均为2
cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.
第4张
B.
第5张
C.
第6张
D.
.第7张
如图,在⊙O中,AE为直径,点C是弧AB的中点,弦AB与半径OC相交于点D,AB=6,CD=1,连接BE,则=( )
A.
B.
C.
D.
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为2,8,则图中三个阴影三角形面积之和为(?
?)
A.
23
B.
19
C.
21
D.
12
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:①BF+GPCD;②(S△ABF)2=S△BEF?S△AFD;③;④.其中结论正确的个数是(
)
A.
5个
B.
4个
C.
3个
D.
2个
二、填空题(本大题共10小题,共30.0分)
如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是____千米.
如图,已知ABCDEF,它们依次交直线、于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于?
?
?
?。
如图,D是△ABC的边AB上一点.请添加一个条件:???????????,使△ACD∽△ABC.
路灯(P点)距地面高9米,身高1.5的小艺站在距路灯的底部(O点)20米的A点,则此时小艺在路灯下的影子长是_________米.
如图,在三角形ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=4:3,则DE:BC=______.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=AB,AF=AD,连结EF交对角线AC于G,则=______.
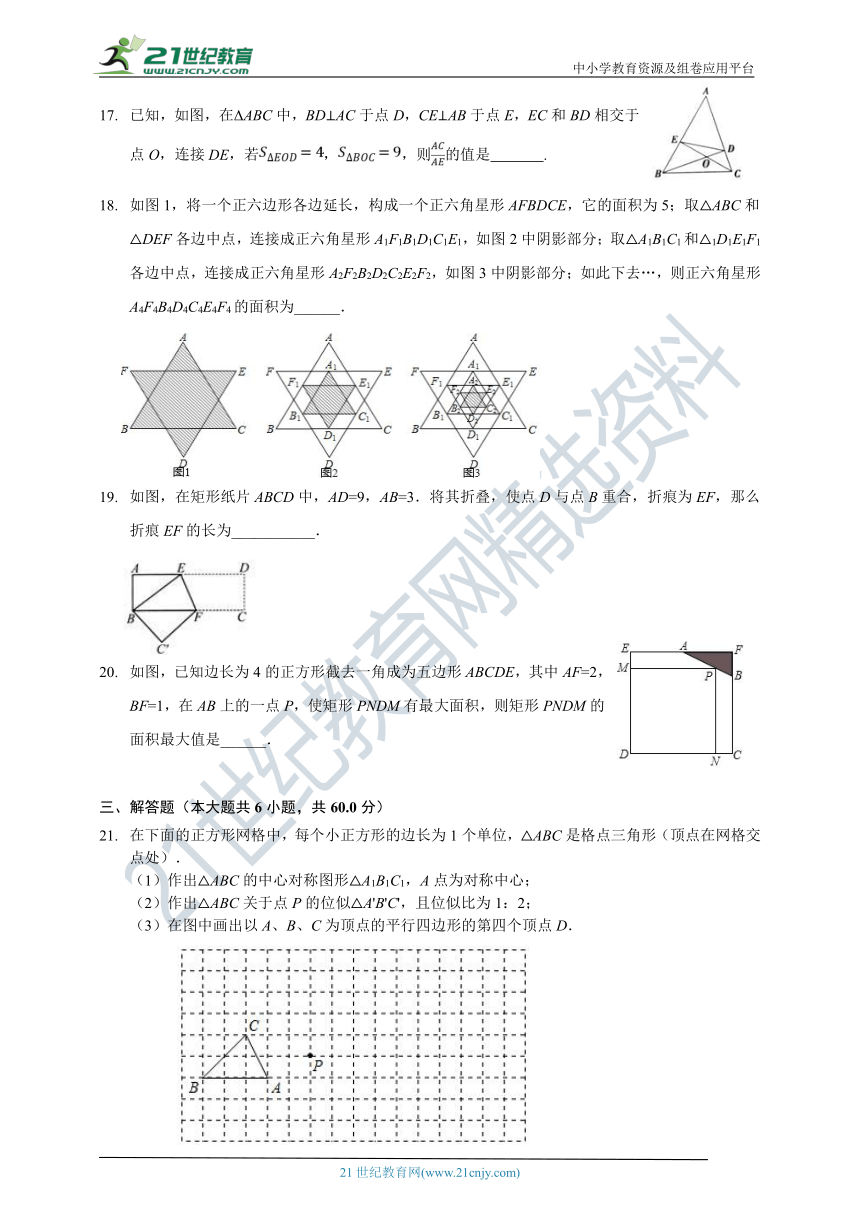
已知,如图,在ΔABC中,BD⊥AC于点D,CE⊥AB于点E,EC和BD相交于点O,连接DE,若,,则的值是??????????????.
如图1,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为5;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图2中阴影部分;取△A1B1C1和△1D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2F2,如图3中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4F4的面积为______.
如图,在矩形纸片ABCD中,AD=9,AB=3.将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为___________.
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1,在AB上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是______.
三、解答题(本大题共6小题,共60.0分)
在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处).
(1)作出△ABC的中心对称图形△A1B1C1,A点为对称中心;
(2)作出△ABC关于点P的位似△A'B'C',且位似比为1:2;
(3)在图中画出以A、B、C为顶点的平行四边形的第四个顶点D.
如图,在中,为边上一点,为边上一点,且
(1)求证:;
(2)求与四边形的面积比.
如图,△ABC中,AC=BC,F为底边AB上一点,=(m,n>0),D是CF中点,联结AD并延长交BC于E.
(1)求的值;
(2)若BE=2EC,求证:CF⊥AB.
如图,ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
=
;
(2)求这个矩形EFGH的宽HE的长.
如图,在中,,,,点P从点A开始,沿AB边以的速度向点B运动:点Q从点B开始,沿BC边以的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.
几秒后的面积等于?
几秒后以P、B、Q为顶点的三角形与相似?
已知ABC=,AB=2,BC=3,ADBC,P为线段BD上的动点,点Q在射线AB上,且满足=(如图所示).
(1)当AD=2,且点Q与点B重合时(如图所示),求线段PC的长.
(2)在图中,连接AP.当AD=,且点Q在线段AB上时,设点B,Q之间的距离为x,
=y,其中表示APQ面积,表示PBC面积,求y关于x的函数解析式,并写出x的取值范围.
(3)当AD答案和解析
1.【答案】B
【解析】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
2.【答案】D
【解析】由△CDO∽△CAF,△COE∽△CFB,△CDE∽△CAB可依次判断各个选项.
本题考查了相似三角形的判定和性质,熟练运用相似三角形的性质是本题的关键.
3.【答案】A
【解析】本题考查了比例的性质,代数式求值.根据比例的性质设x=k,y=3k,z=2k,代入代数式化简后即可得到答案.
4.【答案】D
【解析】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.根据相似三角形的判定定理对各选项进行逐一判定即可.
5.【答案】A
【解析】本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.根据位似变换的概念找出位似中心,根据相似三角形的性质列出比例式,计算即可.
如图点P为位似中心,
∴=,即=,解得PB=3,
∴点P的坐标为(-3,2)
6.【答案】D
【解析】延长DE,BF交于点G,可证△ADE∽△ABC,得DE∥BC,得出BD=DG,可证△EFG∽△CFB,求出EG=BC,则BD-DE的值可求.
本题考查了相似三角形的判定和性质及等腰三角形的判定与性质,正确作出辅助线是解题的关键.
7.【答案】B
【解析】已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是2cm,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为xcm,
则=,解得x=2,
所以另一段长为12-2=10,
因为10÷2=5,所以是第5张.
本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.
8.【答案】D
【解析】设⊙O的半径为r,
∵点C是弧AB的中点,
∴OC⊥AB,AD=DB=3,
在Rt△AOD中,OA2=OD2+AD2,即r2=(r-1)2+32,
解得,r=5,则OD=5-1=4,
∵AD=DB,AO=OE,
∴BE=2OD=8,==
本题考查的是垂径定理、圆周角定理、三角形中位线定理,掌握垂径定理是解题的关键.
9.【答案】C
【解析】已知△A2B1B2,△A3B2B3的面积分别为2,8,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底之边比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为8,可求出△A2B2A3的面积4,同理可求出△A3B3A4和△A1B1A2的面积分别为16和1.即可求出阴影部分的面积.
本题考查了平行线的性质、相似三角形的判定与性质、三角形的面积.解题的关键是利用平行线证明三角形相似,再根据已给的面积,求出相似比,从而求阴影部分的面积.
10.【答案】C
【解析】本题属于四边形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,学会利用面积法解决问题,属于中考压轴题.
①首先作GM⊥BD于点M,根据全等三角形判定的方法,判断出△ABG≌△MBG,即可判断出BM=AB;然后判断出四边形PGMF是矩形,即可推得GP=FM,据此判断出BF+GP=CD即可;
②首先根据AD∥BC,可得,然后根据三角形的面积和底的正比关系,判断出,,即可推得S△ABF2=S△BEF?S△AFD;
③首先根据全等三角形判定的方法,判断出△ABF∽△DBA,即可判断出;然后根据AD=BC,可得AB?BC=AF?BD,据此推得即可;
④首先根据全等三角形判定的方法,判断出△ABG≌△MBG,即可判断出MG=AG;然后判断出AE∥GM,即可推得1,据此判断出即可.
11.【答案】34
【解析】本题主要考查的是比例线段的有关知识,设A、B两地的实际距离是xcm.根据题意列出方程求解即可.
12.【答案】???????
【解析】本题考查了平行线分线段成比例.根据平行线分线段成比例可得到,根据BE=10,即可得到CE的值.
13.【答案】∠ACD=∠B
【解析】根据相似三角形的判定定理:有两角对应相等的两三角形相似,添加条件∠ACD=∠B即可.
14.【答案】4
【解析】此题考查的是相似三角形的判定和性质.本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比可得出小明的影长.根据题意易得:△ABC∽△OBP,利用相似三角形的相似比可得出小明的影长.
15.【答案】4:7
【解析】利用相似三角形的性质:相似三角形的对应角平分线的比等于相似比即可解决问题.
16.【答案】
【解析】根据题意在AD上截取AH=AD,得到AG与AO的关系,然后由相似三角形得到OC与AO的关系,代入求出比值即可.
本题考查的是相似三角形的判定与性质;通过作辅助线证明三角形相似是解决问题的关键.
17.【答案】
【解析】本题考查相似三角形的判定和性质,解答的关键是找到相似三角形.首先证明△AEC∽△ADB,于是可得,,然后证明△AED∽△ACB,于是可得,然后证明△BEO∽△CDO,于是可得,,然后证明△EOD∽△BOC,根据相似三角形的性质可得,问题得解.
18.【答案】
【解析】∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1且相似比为2:1,
∵正六角星形AFBDCE的面积为5,
∴正六角星形A1F1B1D1C1E1的面积为,
同理可得,第二个六角形的面积为:,
第三个六角形的面积为:,
第4个六角形的面积为:=.
故答案为:.
先分别求出第一个正六角星形AFBDCE与第二个边长之比,再根据相似多边形面积的比等于相似比的平方,找出规律即可解答.
19.【答案】
【解析】本题考查的是折叠的性质,矩形的性质,等腰三角形的性质,勾股定理,相似三角形的判定和性质?.连接BD,由折叠的性质知,BE=ED,∠BEG=∠DEG,BG=GD,BD⊥EF,在△ABD中利用勾股定理求得BD的长,利用△BGF∽△BCD,求得GF,从而得到EF的长.?
20.【答案】12
【解析】如图,延长NP交EF于G点,
设PG=x,则PN=4-x,
∵PG∥BF,
∴△APG∽△ABF,
∴=,即=,解得AG=2x,
∴MP=EG=EA+AG=2+2x,
∴S矩形PNDM=PM?PN=(2+2x)(4-x)
=-2x2+6x+8=-2(x-)2+(0≤x≤1),
∵-2<0,PG=x≤BF=1,
∴抛物线开口向下,当x=1时,函数有最大值为12.
本题考查了二次函数的最值的运用.关键是设线段的长,利用相似的性质表示矩形的面积,用二次函数的方法解题.
21.【答案】解:(1)如图所示:△A1B1C1,为所求作的三角形;
(2)如图所示:△A′B′C′为所求作的三角形;
(3)如图所示:D1,D2,D3为所求作的点.
【解析】此题考查了作图-位似变换及旋转变换,以及平行四边形的判定与性质,其中画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形,同时第三问满足题意的点D的位置有3处,注意找全.
22.【答案】(1)证明:∵,
∴==,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,=,
∴=()2=,
∴△ADE与四边形DBCE的面积比是4:5.
【解析】本题考查了相似三角形的性质和判定,能熟记相似三角形的性质和判定的内容是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.
23.【答案】(1)解:如图,过点F作FG∥BC交AE于G,
则∠DFG=∠DCE,∠DGF=∠DEC,
∵D是CF的中点,∴CD=DF,
∴△DCE≌△DFG(ASA),
∴EC=GF,
∵=,
∴,
∵FG∥BC,∴△AFG∽△ABE,
∴,
∴;
(2)证明:若BE=2EC,则BE:EC=2,
由(1)知,=2,
解得:m=n,
∴点F是AB的中点,
∵AC=BC,
∴CF⊥AB.
【解析】本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线,构造出全等三角形和相似三角形是解题的关键.
24.【答案】(1)证明:∵四边形EFGH为矩形,
∴EF∥HG,
∴∠AHG=∠ABC,
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∵AD是边BC上的高,HG∥BC,
∴AM⊥HG,
∴;
(2)解:设HE=xcm,MD=HE=xcm,
∵AD=30cm,∴AM=(30-x)cm,
∵HG=2HE,∴HG=(2x)cm,
由(1)可得
,解得x=12,
∴宽HE的长为12cm.
【解析】此题主要考查了相似三角形的判定与性质,根据矩形性质得出△AHG∽△ABC是解决问题的关键.
25.【答案】解:(1)设t秒后△PBQ的面积等于8
cm,
此时,AP=t,BP=6-t,BQ=2t,
∵,
即,即t2-6t+8=0,解得t1=2,t2=4.
∴2秒或4秒后,△PBQ的面积等于8
cm2;
(2)设x秒后以P,B,Q为顶点的三角形与△ABC相似,
此时,AP=x,BP=6-x,BQ=2x,
①若△BPQ∽△BAC,则,即,解得x=3;
②若△BPQ∽△BCA,则,即,解得x=1.2.
综上所述,1.2秒或3秒后,以P,B,Q为顶点的三角形与△ABC相似.
【解析】本题考查的是相似三角形的性质,熟知相似三角形的判定定理是解答此题的关键,注意分类讨论
26.【答案】解:(1)如图,
在RtABD中,AB=2,AD=2,
==1,D=,
PQ=PC,即PB=PC,
过点P作PEBC,则BE=BC=,
而PBC=D=,
PC=PB=;
(2)在图中,
过点P作PEBC,PFAB于点F,
DAF=PEB=,D=PBE,
RtABDRtEPB,==2=,
设EB=3k,则EP=4k,PF=EB=3k,
=BCPE
=34k=6k,
==ABPF=23k=3k=,
y===,
x取值范围:0x<2;
(3)QPC=.
证明:在图中,
过点P作PEBC,PFAB于点F.A=PEB=,D=PBE,
RtABDRtEPB,=.
又=,
=,
=,RtPQFRtPCE,FPQ=EPC,
EPC+QPE=FPQ+QPE=???????.
【解析】本题是三角形综合题,主要考查相似三角形的判定与性质.
(1)根据题意求得PQ=PC,即PB=PC,再进一步求得答案;
(2)证明RtABDRtEPB,结合三角形的面积,即可求得答案;
(3)过点P作PEBC,PFAB于点F,证明RtABDRtEPB,RtPQFRtPCE,即可求得结论.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
九年级上册数学
相似三角形
单元测试卷
(满分120分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列各组中的四条线段成比例的是( )
A.
a=2,b=3,c=4,d=1
B.
a=2,b=4,c=3,d=6
C.
a=4,b=6,c=5,d=10
D.
a=1,b=2,c=3,d=4
如图,DE∥AB,下列比例式中不成立的是( )
A.
B.
=
C.
=
D.
=
若x:y=1:3,2y=3z,则的值是(
)
A.
-5
B.
-
C.
D.
5
如图,在△ABC中,∠A=75°,AB=6,AC=8,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
A.B.C.D.
如图,两个三角形是以点P为位似中心的位似图形,则点P的坐标是(
)
A.
(﹣3,2)
B.
(﹣3,1)
C.
(2,﹣3)
D.
(﹣2,3)
如图,在△ABC中,BC=9,∠ABC的平分线BF交AC于点F,点D、点E分别是边AB、AC上的点,若,则BD-DE的值为( )
A.
3
B.
3.5
C.
4
D.
4.5
如图,一张等腰三角形纸片,底边长12
cm,底边上的高为12
cm,现沿底边依次向下往上裁剪宽度均为2
cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.
第4张
B.
第5张
C.
第6张
D.
.第7张
如图,在⊙O中,AE为直径,点C是弧AB的中点,弦AB与半径OC相交于点D,AB=6,CD=1,连接BE,则=( )
A.
B.
C.
D.
如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为2,8,则图中三个阴影三角形面积之和为(?
?)
A.
23
B.
19
C.
21
D.
12
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:①BF+GPCD;②(S△ABF)2=S△BEF?S△AFD;③;④.其中结论正确的个数是(
)
A.
5个
B.
4个
C.
3个
D.
2个
二、填空题(本大题共10小题,共30.0分)
如果在比例尺为1:1
000
000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是____千米.
如图,已知ABCDEF,它们依次交直线、于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于?
?
?
?。
如图,D是△ABC的边AB上一点.请添加一个条件:???????????,使△ACD∽△ABC.
路灯(P点)距地面高9米,身高1.5的小艺站在距路灯的底部(O点)20米的A点,则此时小艺在路灯下的影子长是_________米.
如图,在三角形ABC中,D,E分别是AB,AC上的点,AF平分∠BAC,交DE于点G,交BC于点F.若∠AED=∠B,且AG:GF=4:3,则DE:BC=______.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=AB,AF=AD,连结EF交对角线AC于G,则=______.
已知,如图,在ΔABC中,BD⊥AC于点D,CE⊥AB于点E,EC和BD相交于点O,连接DE,若,,则的值是??????????????.
如图1,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为5;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图2中阴影部分;取△A1B1C1和△1D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2F2,如图3中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4F4的面积为______.
如图,在矩形纸片ABCD中,AD=9,AB=3.将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为___________.
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1,在AB上的一点P,使矩形PNDM有最大面积,则矩形PNDM的面积最大值是______.
三、解答题(本大题共6小题,共60.0分)
在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处).
(1)作出△ABC的中心对称图形△A1B1C1,A点为对称中心;
(2)作出△ABC关于点P的位似△A'B'C',且位似比为1:2;
(3)在图中画出以A、B、C为顶点的平行四边形的第四个顶点D.
如图,在中,为边上一点,为边上一点,且
(1)求证:;
(2)求与四边形的面积比.
如图,△ABC中,AC=BC,F为底边AB上一点,=(m,n>0),D是CF中点,联结AD并延长交BC于E.
(1)求的值;
(2)若BE=2EC,求证:CF⊥AB.
如图,ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G,H分别在AC,AB上,AD与HG的交点为M.
(1)求证:
=
;
(2)求这个矩形EFGH的宽HE的长.
如图,在中,,,,点P从点A开始,沿AB边以的速度向点B运动:点Q从点B开始,沿BC边以的速度向点C运动,当点P运动到点B时,运动停止,如果P、Q分别从A、B两点同时出发.
几秒后的面积等于?
几秒后以P、B、Q为顶点的三角形与相似?
已知ABC=,AB=2,BC=3,ADBC,P为线段BD上的动点,点Q在射线AB上,且满足=(如图所示).
(1)当AD=2,且点Q与点B重合时(如图所示),求线段PC的长.
(2)在图中,连接AP.当AD=,且点Q在线段AB上时,设点B,Q之间的距离为x,
=y,其中表示APQ面积,表示PBC面积,求y关于x的函数解析式,并写出x的取值范围.
(3)当AD
1.【答案】B
【解析】此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
2.【答案】D
【解析】由△CDO∽△CAF,△COE∽△CFB,△CDE∽△CAB可依次判断各个选项.
本题考查了相似三角形的判定和性质,熟练运用相似三角形的性质是本题的关键.
3.【答案】A
【解析】本题考查了比例的性质,代数式求值.根据比例的性质设x=k,y=3k,z=2k,代入代数式化简后即可得到答案.
4.【答案】D
【解析】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.根据相似三角形的判定定理对各选项进行逐一判定即可.
5.【答案】A
【解析】本题考查的是位似变换的概念和性质,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.根据位似变换的概念找出位似中心,根据相似三角形的性质列出比例式,计算即可.
如图点P为位似中心,
∴=,即=,解得PB=3,
∴点P的坐标为(-3,2)
6.【答案】D
【解析】延长DE,BF交于点G,可证△ADE∽△ABC,得DE∥BC,得出BD=DG,可证△EFG∽△CFB,求出EG=BC,则BD-DE的值可求.
本题考查了相似三角形的判定和性质及等腰三角形的判定与性质,正确作出辅助线是解题的关键.
7.【答案】B
【解析】已知剪得的纸条中有一张是正方形,则正方形中平行于底边的边是2cm,
所以根据相似三角形的性质可设从顶点到这个正方形的线段为xcm,
则=,解得x=2,
所以另一段长为12-2=10,
因为10÷2=5,所以是第5张.
本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用;由相似三角形的性质得出比例式是解决问题的关键.
8.【答案】D
【解析】设⊙O的半径为r,
∵点C是弧AB的中点,
∴OC⊥AB,AD=DB=3,
在Rt△AOD中,OA2=OD2+AD2,即r2=(r-1)2+32,
解得,r=5,则OD=5-1=4,
∵AD=DB,AO=OE,
∴BE=2OD=8,==
本题考查的是垂径定理、圆周角定理、三角形中位线定理,掌握垂径定理是解题的关键.
9.【答案】C
【解析】已知△A2B1B2,△A3B2B3的面积分别为2,8,且两三角形相似,因此可得出A2B2:A3B3=1:2,由于△A2B2A3与△B2A3B3是等高不等底的三角形,所以面积之比即为底之边比,因此这两个三角形的面积比为1:2,根据△A3B2B3的面积为8,可求出△A2B2A3的面积4,同理可求出△A3B3A4和△A1B1A2的面积分别为16和1.即可求出阴影部分的面积.
本题考查了平行线的性质、相似三角形的判定与性质、三角形的面积.解题的关键是利用平行线证明三角形相似,再根据已给的面积,求出相似比,从而求阴影部分的面积.
10.【答案】C
【解析】本题属于四边形综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,学会利用面积法解决问题,属于中考压轴题.
①首先作GM⊥BD于点M,根据全等三角形判定的方法,判断出△ABG≌△MBG,即可判断出BM=AB;然后判断出四边形PGMF是矩形,即可推得GP=FM,据此判断出BF+GP=CD即可;
②首先根据AD∥BC,可得,然后根据三角形的面积和底的正比关系,判断出,,即可推得S△ABF2=S△BEF?S△AFD;
③首先根据全等三角形判定的方法,判断出△ABF∽△DBA,即可判断出;然后根据AD=BC,可得AB?BC=AF?BD,据此推得即可;
④首先根据全等三角形判定的方法,判断出△ABG≌△MBG,即可判断出MG=AG;然后判断出AE∥GM,即可推得1,据此判断出即可.
11.【答案】34
【解析】本题主要考查的是比例线段的有关知识,设A、B两地的实际距离是xcm.根据题意列出方程求解即可.
12.【答案】???????
【解析】本题考查了平行线分线段成比例.根据平行线分线段成比例可得到,根据BE=10,即可得到CE的值.
13.【答案】∠ACD=∠B
【解析】根据相似三角形的判定定理:有两角对应相等的两三角形相似,添加条件∠ACD=∠B即可.
14.【答案】4
【解析】此题考查的是相似三角形的判定和性质.本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比可得出小明的影长.根据题意易得:△ABC∽△OBP,利用相似三角形的相似比可得出小明的影长.
15.【答案】4:7
【解析】利用相似三角形的性质:相似三角形的对应角平分线的比等于相似比即可解决问题.
16.【答案】
【解析】根据题意在AD上截取AH=AD,得到AG与AO的关系,然后由相似三角形得到OC与AO的关系,代入求出比值即可.
本题考查的是相似三角形的判定与性质;通过作辅助线证明三角形相似是解决问题的关键.
17.【答案】
【解析】本题考查相似三角形的判定和性质,解答的关键是找到相似三角形.首先证明△AEC∽△ADB,于是可得,,然后证明△AED∽△ACB,于是可得,然后证明△BEO∽△CDO,于是可得,,然后证明△EOD∽△BOC,根据相似三角形的性质可得,问题得解.
18.【答案】
【解析】∵A1、F1、B1、D1、C1、E1分别是△ABC和△DEF各边中点,
∴正六角星形AFBDCE∽正六角星形A1F1B1D1C1E1且相似比为2:1,
∵正六角星形AFBDCE的面积为5,
∴正六角星形A1F1B1D1C1E1的面积为,
同理可得,第二个六角形的面积为:,
第三个六角形的面积为:,
第4个六角形的面积为:=.
故答案为:.
先分别求出第一个正六角星形AFBDCE与第二个边长之比,再根据相似多边形面积的比等于相似比的平方,找出规律即可解答.
19.【答案】
【解析】本题考查的是折叠的性质,矩形的性质,等腰三角形的性质,勾股定理,相似三角形的判定和性质?.连接BD,由折叠的性质知,BE=ED,∠BEG=∠DEG,BG=GD,BD⊥EF,在△ABD中利用勾股定理求得BD的长,利用△BGF∽△BCD,求得GF,从而得到EF的长.?
20.【答案】12
【解析】如图,延长NP交EF于G点,
设PG=x,则PN=4-x,
∵PG∥BF,
∴△APG∽△ABF,
∴=,即=,解得AG=2x,
∴MP=EG=EA+AG=2+2x,
∴S矩形PNDM=PM?PN=(2+2x)(4-x)
=-2x2+6x+8=-2(x-)2+(0≤x≤1),
∵-2<0,PG=x≤BF=1,
∴抛物线开口向下,当x=1时,函数有最大值为12.
本题考查了二次函数的最值的运用.关键是设线段的长,利用相似的性质表示矩形的面积,用二次函数的方法解题.
21.【答案】解:(1)如图所示:△A1B1C1,为所求作的三角形;
(2)如图所示:△A′B′C′为所求作的三角形;
(3)如图所示:D1,D2,D3为所求作的点.
【解析】此题考查了作图-位似变换及旋转变换,以及平行四边形的判定与性质,其中画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形,同时第三问满足题意的点D的位置有3处,注意找全.
22.【答案】(1)证明:∵,
∴==,
∵∠A=∠A,
∴△ADE∽△ABC;
(2)解:∵△ADE∽△ABC,=,
∴=()2=,
∴△ADE与四边形DBCE的面积比是4:5.
【解析】本题考查了相似三角形的性质和判定,能熟记相似三角形的性质和判定的内容是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.
23.【答案】(1)解:如图,过点F作FG∥BC交AE于G,
则∠DFG=∠DCE,∠DGF=∠DEC,
∵D是CF的中点,∴CD=DF,
∴△DCE≌△DFG(ASA),
∴EC=GF,
∵=,
∴,
∵FG∥BC,∴△AFG∽△ABE,
∴,
∴;
(2)证明:若BE=2EC,则BE:EC=2,
由(1)知,=2,
解得:m=n,
∴点F是AB的中点,
∵AC=BC,
∴CF⊥AB.
【解析】本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形三线合一的性质,作辅助线,构造出全等三角形和相似三角形是解题的关键.
24.【答案】(1)证明:∵四边形EFGH为矩形,
∴EF∥HG,
∴∠AHG=∠ABC,
又∵∠HAG=∠BAC,
∴△AHG∽△ABC,
∵AD是边BC上的高,HG∥BC,
∴AM⊥HG,
∴;
(2)解:设HE=xcm,MD=HE=xcm,
∵AD=30cm,∴AM=(30-x)cm,
∵HG=2HE,∴HG=(2x)cm,
由(1)可得
,解得x=12,
∴宽HE的长为12cm.
【解析】此题主要考查了相似三角形的判定与性质,根据矩形性质得出△AHG∽△ABC是解决问题的关键.
25.【答案】解:(1)设t秒后△PBQ的面积等于8
cm,
此时,AP=t,BP=6-t,BQ=2t,
∵,
即,即t2-6t+8=0,解得t1=2,t2=4.
∴2秒或4秒后,△PBQ的面积等于8
cm2;
(2)设x秒后以P,B,Q为顶点的三角形与△ABC相似,
此时,AP=x,BP=6-x,BQ=2x,
①若△BPQ∽△BAC,则,即,解得x=3;
②若△BPQ∽△BCA,则,即,解得x=1.2.
综上所述,1.2秒或3秒后,以P,B,Q为顶点的三角形与△ABC相似.
【解析】本题考查的是相似三角形的性质,熟知相似三角形的判定定理是解答此题的关键,注意分类讨论
26.【答案】解:(1)如图,
在RtABD中,AB=2,AD=2,
==1,D=,
PQ=PC,即PB=PC,
过点P作PEBC,则BE=BC=,
而PBC=D=,
PC=PB=;
(2)在图中,
过点P作PEBC,PFAB于点F,
DAF=PEB=,D=PBE,
RtABDRtEPB,==2=,
设EB=3k,则EP=4k,PF=EB=3k,
=BCPE
=34k=6k,
==ABPF=23k=3k=,
y===,
x取值范围:0x<2;
(3)QPC=.
证明:在图中,
过点P作PEBC,PFAB于点F.A=PEB=,D=PBE,
RtABDRtEPB,=.
又=,
=,
=,RtPQFRtPCE,FPQ=EPC,
EPC+QPE=FPQ+QPE=???????.
【解析】本题是三角形综合题,主要考查相似三角形的判定与性质.
(1)根据题意求得PQ=PC,即PB=PC,再进一步求得答案;
(2)证明RtABDRtEPB,结合三角形的面积,即可求得答案;
(3)过点P作PEBC,PFAB于点F,证明RtABDRtEPB,RtPQFRtPCE,即可求得结论.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
