浙教版八年级上册2.1图形的轴对称与翻折专题培优(Word版 附答案)
文档属性
| 名称 | 浙教版八年级上册2.1图形的轴对称与翻折专题培优(Word版 附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 556.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-10 10:59:20 | ||
图片预览


文档简介
2020-2021学年浙教版八年级上册图形的轴对称与翻折专题培优
基础巩固
1.如图是一张长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在A处,点D落在D,处.若∠1
=
40°,则∠BMC的度数为( ).
A.135°
B.120°
C.100°
D.110°
第1题
第2题
第3题
2.如图,△ABC的内部有一点P,且点D,E,F是点P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠BAC
=
70°,∠ABC
=
60°,∠ACB
=
50°,则∠ADB
+
∠BEC
+
∠CFA
=
( ).
A.180°
B.270°
C.360°
D.480°
3.如图,在长方形ABCD中,M为CD的中点,将△MBC沿BM翻折至△MBE,若∠AME
=
a,∠ABE
=
β,则α与β之间的数量关系为( ).
A.a
+
3β
=
180°
B.β
-
α
=
20°
C.α
+
β
=
80°
D.3β
-
2α
=
90°
4.如图,点D,E在△ABC边上,沿DE将△ADE翻折,点A的对应点为点A′,∠A′EC
=
α,∠A′DB
=
β,且α
<
β,则∠A
=
_________
(用含a,β的式子表示).(用含α,β的式子表示).
第4题
第5题
5.如图,设镜面L1和L2,是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A′,A′在镜L中的像为A″,若L1,L2的距离为7,则AA″
=
_________
.
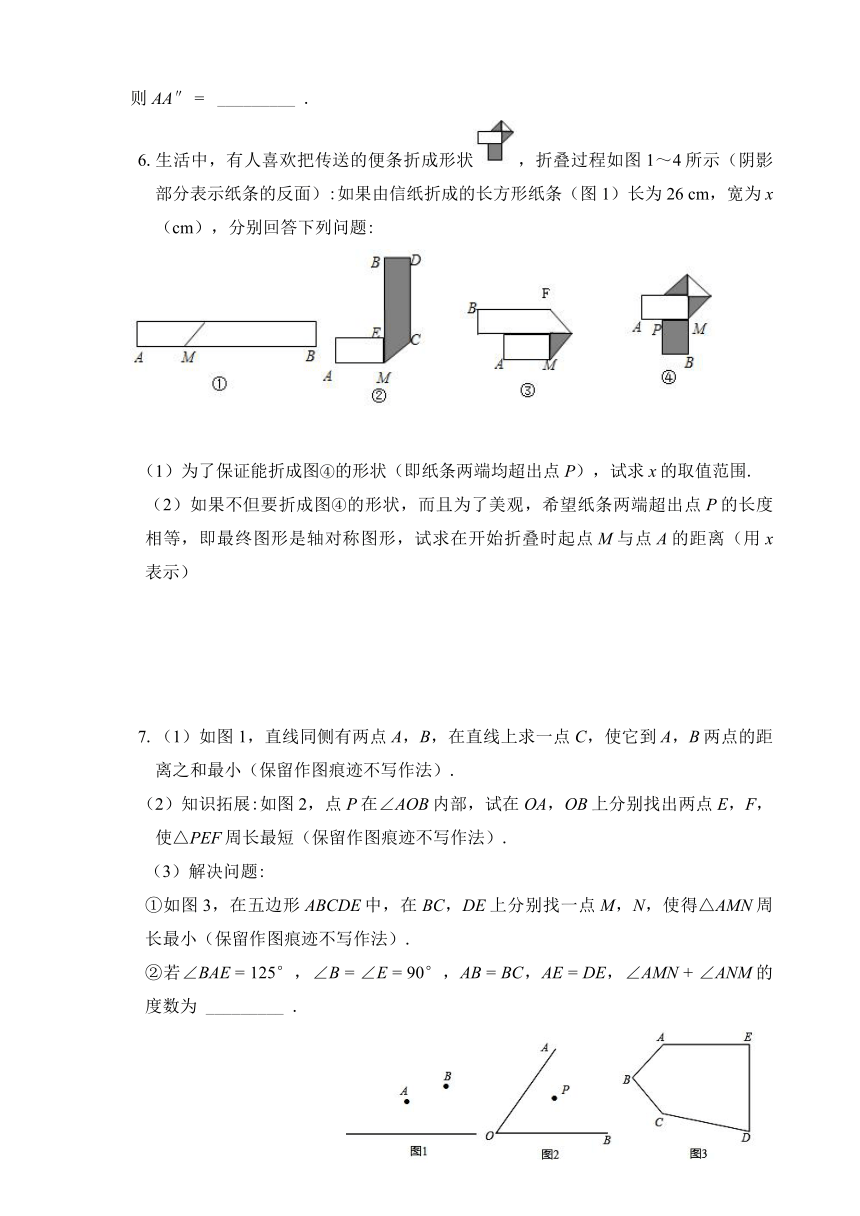
6.生活中,有人喜欢把传送的便条折成形状,折叠过程如图1~4所示(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图1)长为26
cm,宽为x(cm),分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示)
7.(1)如图1,直线同侧有两点A,B,在直线上求一点C,使它到A,B两点的距离之和最小(保留作图痕迹不写作法).
(2)知识拓展:如图2,点P在∠AOB内部,试在OA,OB上分别找出两点E,F,使△PEF周长最短(保留作图痕迹不写作法).
(3)解决问题:
①如图3,在五边形ABCDE中,在BC,DE上分别找一点M,N,使得△AMN周长最小(保留作图痕迹不写作法).
②若∠BAE
=
125°,∠B
=
∠E
=
90°,AB
=
BC,AE
=
DE,∠AMN
+
∠ANM的度数为
_________
.
拓展提优
1.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( ).
A.AD
=
BD
B.AE
=
AC
C.ED
+
EB
=
DB
D.AE
+
CB
=
AB
第1题
2.如图,在△ABC中,AB
=
AC,∠C
=
70°,△AB′C′与△ABC关于直线EF对称,∠CAF
=
10°,连结BB′,则∠ABB′的度数是( ).
A.30°
B.35°
C.40°
D.45°
3.如图,在Rt△ABC中,∠ACB
=
90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A
=
26°,则∠CDE
=
_________
.
4.如图,∠AOB
=
41°,点P为∠AOB内的一点,分别作出点P关于OA,OB的对称点P1,P2,连结P1P2,交OA于点M,交OB于点N,P1P2
=
15,则△PMN的周长为
_________
,∠MPN
=
_________
°.
5.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED
=
4
cm,FC
=
1
cm,∠BAC
=
76°,∠EAC
=
58°.
(1)求出BF的长度.
(2)求∠CAD的度数.
(3)连结EC,线段EC与直线MN有什么关系?
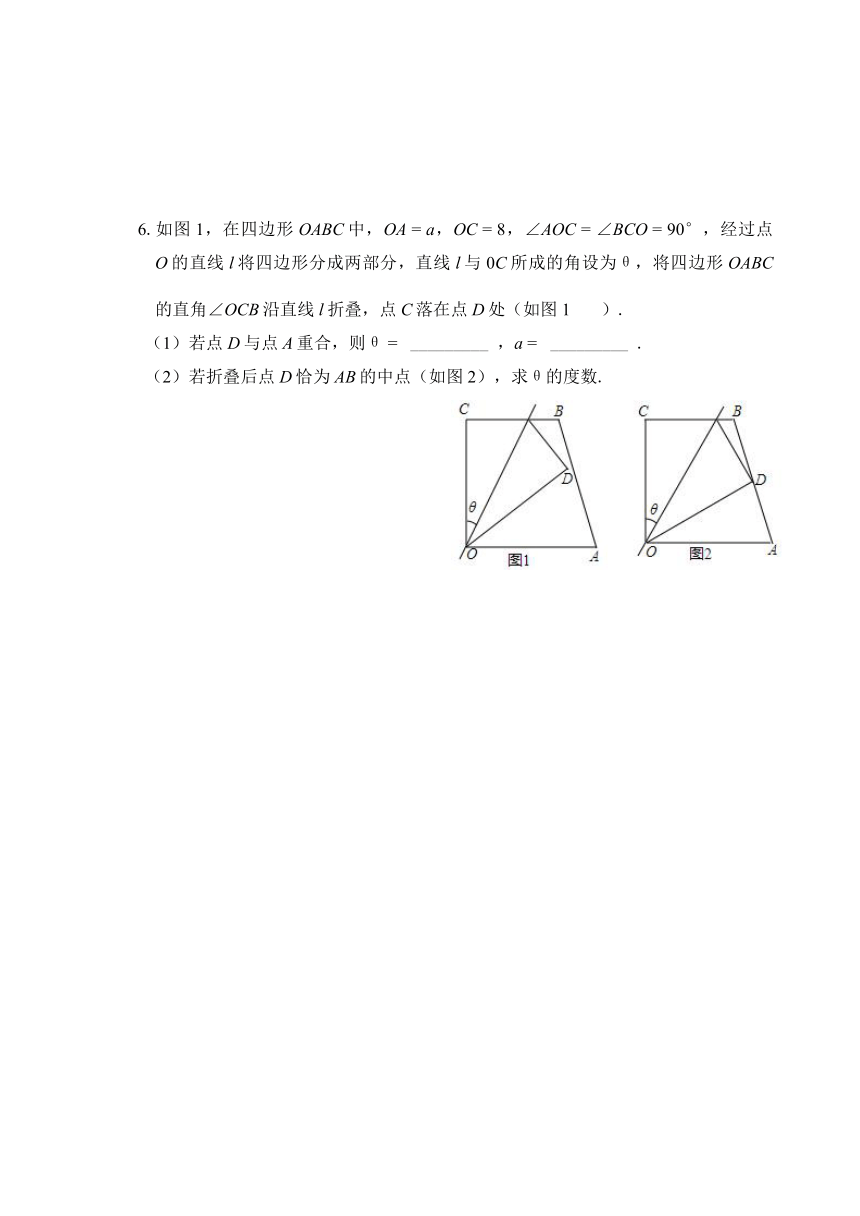
6.如图1,在四边形OABC中,OA
=
a,OC
=
8,∠AOC
=
∠BCO
=
90°,经过点O的直线l将四边形分成两部分,直线l与0C所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若点D与点A重合,则θ
=
_________
,a
=
_________
.
(2)若折叠后点D恰为AB的中点(如图2),求θ的度数.
冲刺重高
1.如图,在四边形ABCD中,∠BAD
=
120°,∠B
=
∠D
=
90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN
+
∠ANM的度数为( ).
A.130°
B.120°
C.110°
D.100°
2.如图,△ABC的BC边上有一小球P,将小球沿着与AB平行的方向击出,撞到点M后反弹,撞击到点N又反弹撞击到点D,若∠ADN
=
105°,则∠A
=
_________
度.
3.如图,已知∠MON
=
50°,P为∠MON内一定点,点A为OM上的点,点B为ON上的点,当△PAB的周长取最小值时,则∠APB度数是
_________
.
4.如图1是长方形纸带,∠DEF
=
26°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是
_________
.
5.在△ABC中,∠CAB
=
2a,且0°
<
α
<
30°,AP平分∠CAB.
(1)如图1,若α=
21°,∠ABC
=
32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
(2)如图2,若∠ABC
=
60°-
α,点P在△ABC的内部,且使∠CBP
=
30°,求∠APC的度数(用含α的代数式表示).
基础巩固
1.如图是一张长方形纸片ABCD,M为AD边的中点,将纸片沿BM,CM折叠,使点A落在A处,点D落在D,处.若∠1
=
40°,则∠BMC的度数为( ).
A.135°
B.120°
C.100°
D.110°
第1题
第2题
第3题
2.如图,△ABC的内部有一点P,且点D,E,F是点P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠BAC
=
70°,∠ABC
=
60°,∠ACB
=
50°,则∠ADB
+
∠BEC
+
∠CFA
=
( ).
A.180°
B.270°
C.360°
D.480°
3.如图,在长方形ABCD中,M为CD的中点,将△MBC沿BM翻折至△MBE,若∠AME
=
a,∠ABE
=
β,则α与β之间的数量关系为( ).
A.a
+
3β
=
180°
B.β
-
α
=
20°
C.α
+
β
=
80°
D.3β
-
2α
=
90°
4.如图,点D,E在△ABC边上,沿DE将△ADE翻折,点A的对应点为点A′,∠A′EC
=
α,∠A′DB
=
β,且α
<
β,则∠A
=
_________
(用含a,β的式子表示).(用含α,β的式子表示).
第4题
第5题
5.如图,设镜面L1和L2,是平行且镜面相对的两面镜子,把一个小球A放在L1,L2之间,小球在镜L1中的像为A′,A′在镜L中的像为A″,若L1,L2的距离为7,则AA″
=
_________
.
6.生活中,有人喜欢把传送的便条折成形状,折叠过程如图1~4所示(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图1)长为26
cm,宽为x(cm),分别回答下列问题:
(1)为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示)
7.(1)如图1,直线同侧有两点A,B,在直线上求一点C,使它到A,B两点的距离之和最小(保留作图痕迹不写作法).
(2)知识拓展:如图2,点P在∠AOB内部,试在OA,OB上分别找出两点E,F,使△PEF周长最短(保留作图痕迹不写作法).
(3)解决问题:
①如图3,在五边形ABCDE中,在BC,DE上分别找一点M,N,使得△AMN周长最小(保留作图痕迹不写作法).
②若∠BAE
=
125°,∠B
=
∠E
=
90°,AB
=
BC,AE
=
DE,∠AMN
+
∠ANM的度数为
_________
.
拓展提优
1.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( ).
A.AD
=
BD
B.AE
=
AC
C.ED
+
EB
=
DB
D.AE
+
CB
=
AB
第1题
2.如图,在△ABC中,AB
=
AC,∠C
=
70°,△AB′C′与△ABC关于直线EF对称,∠CAF
=
10°,连结BB′,则∠ABB′的度数是( ).
A.30°
B.35°
C.40°
D.45°
3.如图,在Rt△ABC中,∠ACB
=
90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A
=
26°,则∠CDE
=
_________
.
4.如图,∠AOB
=
41°,点P为∠AOB内的一点,分别作出点P关于OA,OB的对称点P1,P2,连结P1P2,交OA于点M,交OB于点N,P1P2
=
15,则△PMN的周长为
_________
,∠MPN
=
_________
°.
5.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.若ED
=
4
cm,FC
=
1
cm,∠BAC
=
76°,∠EAC
=
58°.
(1)求出BF的长度.
(2)求∠CAD的度数.
(3)连结EC,线段EC与直线MN有什么关系?
6.如图1,在四边形OABC中,OA
=
a,OC
=
8,∠AOC
=
∠BCO
=
90°,经过点O的直线l将四边形分成两部分,直线l与0C所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处(如图1).
(1)若点D与点A重合,则θ
=
_________
,a
=
_________
.
(2)若折叠后点D恰为AB的中点(如图2),求θ的度数.
冲刺重高
1.如图,在四边形ABCD中,∠BAD
=
120°,∠B
=
∠D
=
90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN
+
∠ANM的度数为( ).
A.130°
B.120°
C.110°
D.100°
2.如图,△ABC的BC边上有一小球P,将小球沿着与AB平行的方向击出,撞到点M后反弹,撞击到点N又反弹撞击到点D,若∠ADN
=
105°,则∠A
=
_________
度.
3.如图,已知∠MON
=
50°,P为∠MON内一定点,点A为OM上的点,点B为ON上的点,当△PAB的周长取最小值时,则∠APB度数是
_________
.
4.如图1是长方形纸带,∠DEF
=
26°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数是
_________
.
5.在△ABC中,∠CAB
=
2a,且0°
<
α
<
30°,AP平分∠CAB.
(1)如图1,若α=
21°,∠ABC
=
32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
(2)如图2,若∠ABC
=
60°-
α,点P在△ABC的内部,且使∠CBP
=
30°,求∠APC的度数(用含α的代数式表示).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
