一次函数复习

(共72张PPT)
一次函数综合复习课
复习
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量.
2.什么叫函数
1.什么叫常量，变量
1、指出下列各式子中的自变量,
因变量,常量,函数.
(1)C＝2πr (r≥0)，
(2)s＝60t (t≥0)，
(3)S＝(n－2)×180 ，
1.某市出租车起步价是7元（路程小于或等于3千米），超过3千米每增加1千米加收1.2元。
（1)你能写出出租车车费y（元）与行程x（千)米）之间的函数关系式吗
(２) 李老师乘车８千米，应付多少车费？
3.怎样求函数解析式
｛
公式法
待定系数法
4.什么叫函数值，怎样求
y=7+1.2(x-3)(x>3)
2.我国是一个严重缺水的国家，我们都应倍加珍惜水资源，节约用水，据测试，拧不紧的水龙头每秒会滴下2滴水，每滴水约0.5毫升，小红同学在洗手时，没有拧紧水龙头，则水龙头滴了y(毫升）水与小红离开x（小时）的函数解析式是 。
3.已知y是x一次函数，当x=3时，y=1；当x=-2时，y=-14。求y关于x的函数解析式；
总滴水=每秒单位×每滴水单位×时间
公式法
y
=
2
×
0.5
×
3600x
5.什么叫一次函数
一般地，函数y=kx+b(k≠0,)叫一次函数
下列函数关系式中，哪些是一次函数？哪些是正比例函数？
它是一次函数，也是正比例函数。
（1）C=2πr
（2）y= x+200
2
3
（3）t=
200
v
（4）y=2（3-x）
（5）S=x（50+x）
它是一次函数，不是正比例函数。
它不是一次函数。
它是一次函数，不是正比例函数。
它不是一次函数。
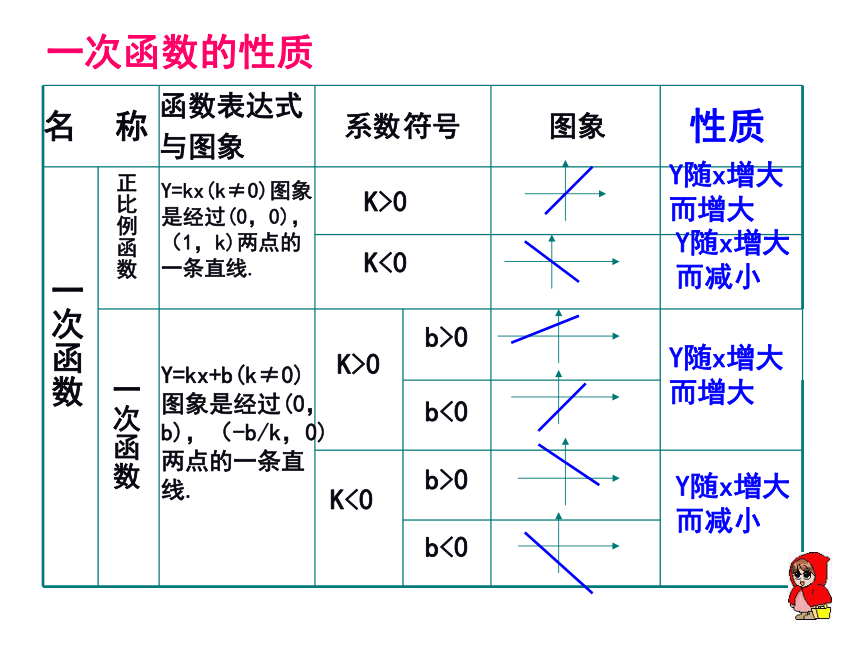
一次函数的性质
名 称 函数表达式
与图象 系数 符号 图象 性质
一次函数
正比例函数
一次函数
Y=kx(k≠0)图象是经过(0，0)，（1，k)两点的一条直线.
K>0
K<0
K>0
K<0
Y=kx+b(k≠0)图象是经过(0，b)，（-b/k，0)两点的一条直线.
b>0
b<0
b<0
b>0
Y随x增大而增大
Y随x增大而减小
Y随x增大而增大
Y随x增大而减小
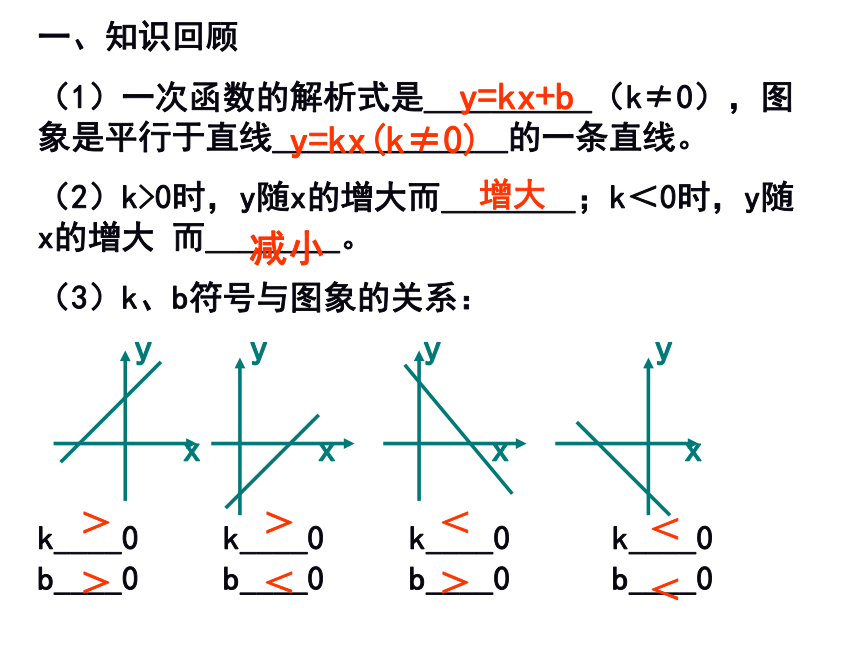
一、知识回顾
（1）一次函数的解析式是＿＿＿＿＿（k≠0），图象是平行于直线＿＿＿＿＿＿＿的一条直线。
（2）k>0时，y随x的增大而＿＿＿＿；k＜0时，y随x的增大 而＿＿＿＿。
（3）k、b符号与图象的关系：
k____0 k____0 k____0 k____0 b____0 b____0 b____0 b____0
y y y y
x x x x
y=kx+b
y=kx(k≠0)
增大
减小
＞
＞
＞
＜
＜
＞
＜
＜
二、主要的知识与应用问题
1.求一次函数解析式的问题
2.求一次函数性质有关问题
3. 看函数的图象及画图象问题
5.求一次函数应用问题
4.求一次函数交点问题及面积问题
1.求一次函数解析式问题的类型
（1）.已知小红的家与学校的距离为600米，小红从家骑自行车出发的速度为6米/秒，则小红离学校的距离s与行驶的时间为t的函数表达式 。
（2）、已知y是x的一次函数，且当x=-2时，y=7；当x=3时，y=-5。求这个一次函数的解析式。
S=600-6t
（4）、已知一次函数的图象与坐标轴交于点（０，１），（１，０），求这个一次函数的解析式．
（3）已知y+m与x-1成正比例，当x=-1时，y=-15
；当x=7时，y=1。求:y关于x的函数解析式；
(5).一次函数y=kx+b的图象如图所示，则y关于x的函数解析式
x
y
0
1
2
3
3
1
2
-1
-2
-2
-1
（6）、某商店售货时，在进价基础上加一定利润，销量x（千克）与售价y（元）如下表所示：
销量x（千克） 1 2 3 4 5 …
售价y（元） 6+0.4 14+0.8 22+1.2 30+1.6 38+2.0 …
判断变量x、y是否满足一次函数关系式，如果是，求出解析式，并求当销量为2.5千克时的售价。
（7）如图所示摆放，
n=1 n=2 n=3
s=4 s=6 s=8
则s与n的函数关系式是 。
S=2n+2
2.求一次函数性质有关问题
(1).一次函数y=-2x+b的图象有两点A（-1，y1）,
B（2，y2),则y1 y2
(2).对于函数 ，当 -1(3).在一次函数y=(2m+2)x+5中，y随着x的增大
而减小，则m的范围是 。
>
3
≤9
m<-1
（4）.某函数具有下列两个性质：
（1）它的图象是经过点（－1，2）的一条直线； （2）函数值随自变量的增大而增小； 请写出符合上述条件的一个函数解析式：___________
y=-3x-1
（5）如图，已知一次函数y=3x－3，则y=3x—3
与x轴的交点B为 。
当x____时，y>0；
当x____时，y=0；
当x____时，y<0。
(1，0)
B
A
x
y
>1
<1
=1
(1，0)
3.怎么看函数的图象及画图象问题
（1）. 画出下列函数图象
（2）.某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产了3小时后安排工人装箱，若每小时装产品150件，未装箱的产品数量(y)是时间(t)的函数，这个函数的大致图象只能是 ( )
A
（3）图1是水滴进玻璃容器的示意图（滴水速度不变），图2是容器中水高度随滴水时间变化的图像.
给出下列对应：（1）：（a）——（e） （2）：（b）—（f）（3）：（c）—h （4）：（d）—（g）其中正确的是( )
（A）（1）和（2） （B）（2）和（3）
（C）（1）和（3） （D）（3）和（4）
C
（4）下图是某蓄水池的横断面示意图，分深水区和浅水区，如果这个蓄水池以固定的流量注水，图11-2中能大致表示水的最大深度h与时间t之间关系的是( )．
C
（5）下列图形中，表示一次函数y = mx + n与正比例函数y = mnx（m、n为常数，且mn≠0）的图象的是（ ）
A
O
y
x
B
O
y
x
C
O
y
x
D
O
y
x
A
（6）两条直线y1＝ax＋b与y2＝bx＋a在同一坐标系中的图象可能是下图中的 ( )
A
（7）一次函数y1=kx+b与y2=x+a的图象如图，则下列结论①k＜0；②a＜0；③当x＞3时，y1＜ y2中，正确的个数是（ ）
A、0 B、1 C、2 D、3
C
（8）如图中的图象（折线ABCDE）描述了一汽车在某一
直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：
①汽车共行驶了120千米；
②汽车在行驶途中停留了
0.5小时；
③汽车在整个行驶过程中
的平均速度为 千米/时；
④汽车自出发后3小时
至4.5小时之间行驶的
速度在逐渐减少.其中
正确的说法共有（ ）
A、1个 B、2个
C、3个 D、4个
A
（9）甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,给出下列说法:
(1)他们都骑行了20km;
(2)乙在途中停留了0.5h;
(3)甲、乙两人同时到达
目的地;
(4)相遇后,甲的速度小于
乙的速度.
根据图象信息,以上说法
正确的有( )
A.1个 B.2个
C.3个 D.4个
C
（10）如图，一次函数y=kx+b的图象经过A、B两点，则kx+b>0的解集是( )
A. x>0 B. x>2 C. x>-3 D. -3C
（11）.如图中，l1反映了某公司产品的销售额与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图象判断该公司盈利时销售量为（ ）
（A）小于4件
（B）大于4件
（C）等于4件
（D）大于或等于4件
X（件）
Y（元）
1
2
3
4
5
6
100
200
300
400
500
l1
l2
O
B
（12）如图，某电信公司提供了两种方案的移动通讯费用（元）与通话时间（元）之间的关系，则以下说法错误的是（ ）
A．若通话时间少于120分，则方案比方案便宜20元
B．若通话时间超过200分，
则方案比方案便宜12元
C．若通讯费用为60元，
则方案比方案的通话
时间多
D．若两种方案通讯
费用相差10元，则通
话时间是145分或185分
70
50
30
120
170
200
250
x（分）
y（元）
A方案
B方案
（第12题）
D
4.求一次函数交点问题及面积问题
1、已知一次函数
（1）求该函数的图象与坐标轴围成的图形的 面积；
（2）求该函数与两坐标轴交点间的距离；
（3）求原点到直线y=-x+3的距离。
2、已知y-4与x成正比例，且当x=6时，y=-4.
（1）求y与x的函数关系式；
（2）设点P在y轴的负半轴上，（1）中函数的图像与x轴、y轴分别交于A、B两点，且以A、B、P为顶点的三角形面积为9，试求点P的坐标．
3、若直线y=2x+3与y=3x-2b相交于x轴，则b 的值是( )．
A．-3 B．- C．6 D．-
4、已知一次函数图象过点P（0，－2）且与两坐标轴截得的直角三角形面积为3.确定该一次函数解析式.
D
5、已知直线ｙ＝kx+1(k>0)，求k为何值时与坐标轴所围成的三角形的面积等于1。
6、已知一次函数y=kx+b的图象经过点M（-1，1）及点N（0，2），设该图象与x轴交于点A，与y轴交于点B，问：在x轴上是否存在点P，使ABP为等腰三角形？若存在，把符合条件的点P的坐标都求出来；若不存在，请说明理由。
7、两条直线y=-1.5x与y=2x+5及y轴围成的三角形的面积。
8、已知直线l与直线y＝2x＋1的交点横坐标为2，与直线y＝－x－8的交点的纵坐标为－7，求直线l的解析式．
当Ｘ为何值时？
（３）ｙ１＜ｙ２
（２）ｙ１＞ｙ２
（１）ｙ１＝ｙ２
在直线ｙ＝x＋１上是否存在点Ｍ，使Ｓ⊿ADM= 2Ｓ⊿ADP.
M
9、已知一次函数y=kx+b（k、b是常数，且k≠0），x与y的部分对应值如下表所示，那么不等式kx+b<0的解集是（ ）
X －2 －1 0 1 2 3
y 3 2 1 0 －1 －2
A、x<0 B、x>0 C、x<1 D、x>1
D
例1 已知一次函数
(1) k为何值时,它的图象经过原点
(2)k为何值时,它的图象经过点(0, -2)
(3)k为何值时,它的图象平行直线 y= -x
(4) k为何值时,它的图象向下平移后，变成直线y=2x+8
(5)k 为何值时,y随x的增大而减小
5.求一次函数应用问题
例2、一条直线经过点A（0，4），点B（2，0），现将这条直线沿x轴向左平移3个单位，则平移后的函数解析式为（ ）
A.y=-2x+4 B.y=-2x-1
C.y=-2x-2 D.y=-2x+1
C
例2 已知函数
(1)当x=0时, y =
(2 )当x=5时, y=
(3)当y=0时, x=
(4)当y＞0时, x的取值范围是
(6)当－3≤y≤0时, x的取值范围是
(5)当y＜1 时, x的取值范围是
-3
7
1.5
x＞1.5
x＜2
0＜x＜1.5
例3、拖拉机开始工作时，油箱中有油24升，如果每小时耗油4升，那么油箱中的剩油量y（升）与工作时间x（时）之间的函数关系式和图象是（ ）
y y y y
－24
0 x
24
O 6 X
24
6
O
X
O
6
－24
X
y=4x－24
(0≤x ≤6)
y=－4x+24
y=4x－24
y=24－4x
(0 ≤ x ≤ 6)
D
A
B
C
D
例4：如图所示，向高为H的圆柱形杯中注水，已知水杯底面半径为2，那么注水量y与水深x的函数关系的图象是（ ）
------
---------
----
－－
－
●
●
●
A
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
例5、旅客乘车按规定可随身携带一定重量的行李，如果超过规定，则需购行李票，该行李费y（元），行李重量x（kg）的一次函数，如图所示。
求：（1）y与x之间的函数关系式；
（2）旅客最多可免费携带多少
行李的重量。
----------
--------
-----
---
y(元)
x(kg)
90
60
10
5
O
解：（1）设一次函数关系式为y=kx＋b（k≠0）
把x＝60，y＝5和x＝90，y＝10代入得
5=60k＋b
10=90k＋b
1
6
∴一次函数关系式为y=－x－5
（2）当y＝0时，x＝30
∴旅客最多可免费携带的行李重量是30kg 。
1
6
k=－
b=－5
（x≥30）
例6：
为了缓解用电紧张的矛盾，电力公司制定了新的用电收费标准，每月用电量x（千瓦时）与应付电费y（元）的关系如图所示：
25
50
75
100
25
50
75
100
70
X（千瓦时）
Y（元）
0
（1）根据图象求出y与x的函数关系式；
（2）请回答电力公司的收费标准是什么？
例7：要从甲乙两个仓库向AB两工地运送水泥，已知甲仓库可运出100吨水泥，乙仓库可运出80吨水泥；A工地需70吨水泥，B工地需110吨水泥。两仓库到A，B两工地的路程和每吨每千米的运费如下表：
路程（千米）
甲仓库 乙仓库 运费（元/吨·千米）
甲仓库 乙仓库
A工地 20 15 1.2 1.2
B工地 25 20 1 0.8
（1）设甲仓库运往A地水泥x吨，求总运费y关于x的函数解析式，并画出图象
x
70-x
1.2×20x
1.2×15×(70-x)
100-x
10+x
1×25×(100-x )
0.8×20×(10+x)
甲仓库
乙仓库
A工地
B工地
解：由题意可得
y=1.2×20 x +1×25×(100- x)+1.2×15×(70-x)+0.8
×20[110-(100-x)]
= -3x+3920
即： 所求的函数关系式为 y= -3x+3920 ,其中
0≤x≤70
3500
3710
3920
4000
40
60
80
3000
（吨）
（元）
解：由题意可得
y=1.2×20x+1×25×(100-x)+1.2×15×(70-x)+0.8×20[110-(100-x)]
= -3x+3920
即： 所求的函数关系式为y=-3x+3920 ,其中 0≤x≤70
问题（2）：当甲、乙仓库各运往A、B两工地多少吨水泥时，总运费最省？
解：在一次函数y=-3x+3920 中，K<0 所以y随着
x的增大而减小
因为0≤x≤70 ，所以当 x = 70 时，y的值最小
当x = 70 时，y = -3 x +3920 = -3×70+3920=3710(元）
当甲仓库向A工地运送70吨水泥，则他向B工地运送30吨水泥；乙仓库不向A工地运送水泥，而只向B工地运送80吨时，总运费最省
1、 有下列函数：
①　　　　 　 , ②　　　 ,
③ , ④ 。
其中图象过原点的是 ；
函数 y 随 x 的增大而减小的是 ；
图象过第一、二、三象限的是 。
④
③
②
２、已知点A（-1，a），B（3，b）在函数y=3x+ 4 的图象上，则a与b的大小关系是（ ）
（Ａ）a > b 　　（Ｂ）a = b
（Ｃ） a < b （Ｄ）不能比较
Ｃ
(A) 　　　　 　(B) 　 （C） 　　 （D）
３、已知一次函数y=kx+b , y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( 　)
A
5、在函数 中，自变量x的取值范围是
　　　　　　　　．
6、函数 中，自变量x的取值范围是
　　　　　　　　．
4、在函数 y= -2x+3 中，自变量x的取值范围是
　　　　　　　　．
x为全体实数
x≠2的实数
x≤3
8、如果方程组
则一次函数y=-2x+4与一次函数y=1－x
的交点为__________
9、若两个一次函数 y=x+ 1与y=2x—1的图
象有交点(2，3)，则方程组
的解是___________
7、将二元一次方程3x-2y=l化为y是x的一次函数是______
y =1.5x-0.5
(3,-2)
{
X=2
Y=3
10、若函数y=kx+b(k,b为常数)的图象如图所示，那么,当y﹥0时，x的取值范围是(　　　)
A、x﹥1　B、x﹥2　C、x﹤1　D、x﹤2
11、已知一次函数y=kx+b的图象如图所示，当x＜0时，y的取值范围是（ ）
A．y＞0 B、y＜0
C、－2＜y＜0 D．y＜－2
12、在函数y=2x+3中，当自变量x满足______时，图象在第一象限．
D
D
x﹥0
13、无论m为何实数，直线y=x+2m与y=-x+4的交点不可能在 （ ）
A.第一象限 B.第二象限
C.第三象限 D.第四象限
14、如果正比例函数y=kx（k≠0）的自变量取值增加1，函数y的值相应减少4，则k的值为（ ）
A、4 B、－4 C、 D、-
C
B
15、一次函数 y=3x+b 的图象与两坐标轴围成的三角形的面积为48,求b的值.
16、 设点P(3,m),Q(n,2)都在函数y=x+b的图象上,
求m+n的值.
17、点P(x，y)在第一象限，且x+y=10，点A的坐标为（8，0），设△OPA的面积为S。
用含x的解析式表示S，写出x的取值范围，画出函数S的图象。
x
y
o
·
A
·
8
P
B
即S=4y
∵x+y=10
∴ y=10-x
∴ 这个函数的解析式为S=-4x+40
解:(1)依题意得右图
∴ S=4(10-x)
(0= OA·PB
= ×8y
=4y
S△OPA
∴ S= -4x+40
18、如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出.
(1)当他们行走3小时后，他们之间的距离
为 千米.
(2)当他们之间的距离
为9千米时,他们行走
了 小时
19、某地市话收费标准为：通话时间在三分钟以内（包括三分钟），话费为每分钟0.6元；通话时间超过了三分钟，超过部分按每分钟0.2元。则总话费y（元）与通话时间x（取整）之间的关系式为 ：
X取整数
20、某音像社对外出租光盘的收费方法是：每张光盘在出租头两天每天收0.8元，以后每天收0.5元，那么，一张光盘在出租后第n天（n是大于2的整数），应收租金y=__________.
21、一次函数y=k1x-4与正比例函数y=k2x的图象经过点（2，-1），
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积。
1、一快车和一慢车沿相同路线从A地到B地，所行路程
与时间的函数图象如图所示。则：
0
2
14
18
276
X（时）
Y（千米）
快车
慢车
6
（1）慢车比快车早出发 小时，
快车比慢车早 小时到达B地
（2）快车追上慢车时行驶了
_______千米
（3）慢车速度为 快车速
度为_______
（4）图中快车离开A地的路程y与时间x的函数解
析式 为____________________
2
4
276
46千米/时
69千米/时
Y = 69x - 138
2、在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度y（厘米）与燃烧时间x（小时）之间的关系如图10所示，请根据图象所提供的信息解答下列问题：
（1）甲、乙两根蜡烛燃烧前的高度分别是 ，从点燃到燃尽所用的时间分别是 。
（2）分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
（3）燃烧多长时间时，甲、乙两根蜡烛的高度相等（不考虑都燃尽时的情况）？
在什么时间段内，甲蜡烛比乙蜡烛高？
在什么时间段内，甲蜡烛比乙蜡烛低？
30cm
25cm
2时
2.5时
y甲=-15x+30
y乙=-10x+25
x=1
x>1
x<1
3、某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：
根据图象解答下列问题：
(1)洗衣机的进水时间是多少分钟？
(2)清洗时洗衣机中的水量是多少升？
(3)已知洗衣机的排水速度为每分钟19升，
①求排水时y与x之间的关系式。
②如果排水时间为2分钟，求排水
结束时洗衣机中剩下的水量。
4分钟
40升
y= -19x+325
2升
4、某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后。
（1）服药后______时，血液中含药量最高，
达到每毫升_______毫克，接着逐步衰弱。
（2）服药5时，血液中含药量为每毫升____毫克。
x/时
y/毫克
6
3
2
5
O
3
6
3
x/时
y/毫克
6
3
2
5
O
（3）当x≤2时y与x之间的函数关系式是_____。
（4）当x≥2时y与x之间的函数关系式是____。
（5）如果每毫升血液中含药量3毫克或3毫克以上
时，治疗疾病最有效，那么这个有效时间范围是___时。.
y=3x
y＝-x+8
1~5
5、为迎接2008年北京奥运会，某学校组织了一次野外长跑活动，参加长跑的同学出发后，另一些同学从同地骑自行车前去加油助威。如图，线段L1，L2分别表示长跑的同学和骑自行车的同学行进的路程y（千米）随时间x（分钟）变化的函数图象。根据图象，解答下列问题：
（1）分别求出长跑
的同学和骑自行车的
同学的行进路程y与
时间x的函数表达式；
（ 2）求长跑的同学
出发多少时间后，骑
自行车的同学就追上
了长跑的同学？
6、宁安市与哈尔滨市两地相距360千米.甲车在宁安市，乙车在哈尔滨市，两车同时出发，相向而行，在A地相遇.为节约费用（两车相遇并换货后，均需按原路返回出发地），两车换货后，甲车立即按原路返回宁安市.设每车在行驶过程中速度保持不变，两车间的距离y（千米）与时间x（小时）的函数关系如图所示.根据所提供的信息，回答下列问题：
⑴甲车的速度: ;
乙车的速度: ;
⑵说明从两车
开始出发到5小
时这段时间乙
车的运动状态
y
x
O
200
2
（千米）
3
5
（小时）
360
7、小张骑车往返于甲、乙两地，距甲地的路程y(千米)与时间x(小时)的函数图象如图所示．
（1）小张在路上停留______小时，他从乙地返回时骑车的速度为_______千米/时．
（2）小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止．途中小李与小张共相遇3次．请在图中画出小李距甲地的路程y(千米)与时间x(小时)的函数的大致图象．
（3）小王与小张同时出
发，按相同的路线前往
乙地，距甲地的路程y(千
米)与时间x(小时)的函
数关系为．小王与小张
在途中共相遇几次？请
你计算第一次相遇的时间．
8、有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图11是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：
（1）乙队开挖到30米时，用了_____小时．开挖6小时时，甲队比乙队多挖了______米；
（2）请你求出：
①甲队在0≤x≤6的时段内，y与x之间的函数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
③开挖几小时后，甲队所挖掘河
渠的长度开始超过乙队？
（3）如果甲队施工速度不变，
乙队在开挖6小时后，施工速
度增加到12米/时，结果两队
同时完成了任务．问甲队从
开挖到完工所挖河渠的长度
为多少
y(米)
6
2
O
x(时)
30
60
乙
甲
50
9、如图为甲、乙两名选手在一次自行车越野赛中，路程y（千米）随时间x（分）变化的图象（全程）．根据图象回答下列问题：
（１）比赛开始多少时间时，两人第一次相遇？
（２）这次比赛全程是多少千米？
（３）比赛开始多少时间时，两人第二次相遇？
C
Y（千米）
6
O
7
5
15
24
33
43
48
X（分）
A
B
甲
乙
……
D
F