相似三角形

(共19张PPT)
请同桌合作量一量这两个三角形的三个内角和三条边,并作好记录,思考下面三个小问题．
问题3:这两个三角形对应边的之间比值是多少
问题2:这两个三角形对应边之间有什么关系
问题1:这两个三角形对应角之间有什么关系
4.2 相似三角形
一般地，对应角相等,对应边成比例的两个三角形,叫做相似三角形.
相似用符号“∽”来表示,读做“相似于”
如△ABC与△A’B’C’相似,
记作“△ABC ∽△A’B’C’ ”
注意:在表示三角形相似时,一般对应的 字母写在对应的位置上.
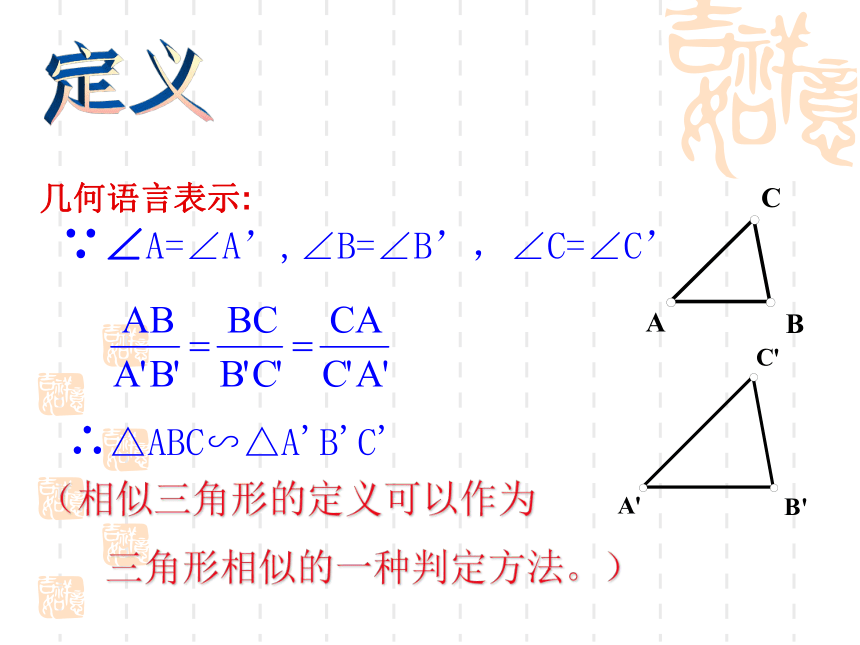
几何语言表示:
∵∠A=∠A’,∠B=∠B’，∠C=∠C’
∴△ABC∽△A'B'C'
（相似三角形的定义可以作为
三角形相似的一种判定方法。）
1、两个等腰三角形一定相似 （ ）
2、两个直角三角形一定相似 （ ）
3、两个全等的三角形一定相似 （ ）
4、两个等边三角形一定相似 （ ）
5、两个等腰直角三角形一定相似 （ ）
6、相似于同一个三角形的两个三角形一定相似 （ ）
×
×
√
√
√
√
判断下面各题，并说明理由。
相似三角形的传递性
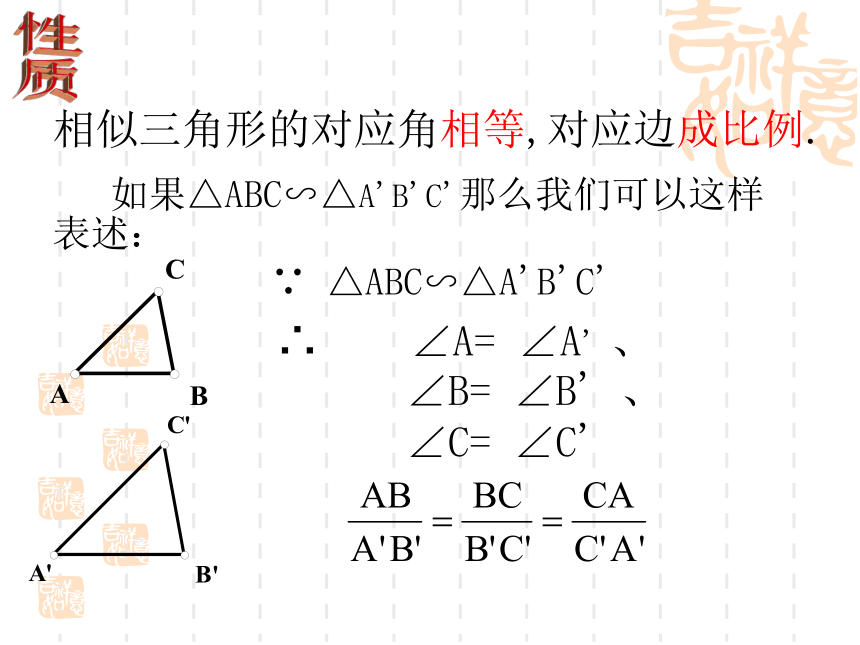
如果△ABC∽△A'B'C'那么我们可以这样表述：
∴ ∠A= ∠A' 、
∠B= ∠B' 、
∠C= ∠C'
∵ △ABC∽△A'B'C'
相似三角形的对应角相等,对应边成比例.
（2）、已知△ABC∽△ A'B'C' ，如果∠A=55°，
∠B=100°，∠C'的度数为（　）
Ａ. 100°Ｂ. 55°　Ｃ. 30°Ｄ.25°　
初显身手
（１）、如图，△ABC∽△ADE，已知，
＝ ，则 ＝ ＿＿＿＿。
（3）、已知△ABC的三边长分别是3，4，5，与其相似的三角形△DEF的最大边是15，则△DEF的周长等于＿＿。
36
2
5
D
请同学们动手摆一摆，使它们有一个公共顶点，你能摆出多少种不同位置关系的图形。
E
D
C
B
A
E
D
C
B
A
E
D
C
B
A
X型
A型
非A型
已知,如图,D,E分别是△ABC的边AB,AC反向延长线上的点,△ADE∽△ABC.AD﹕DB=1﹕4,BC=9cm,求DE的长.
A
E
D
C
B
已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
证明：
∵D，E分别是AB，AC的中点，
∴∠ADE=∠B，∠AED=∠C
在△ADE和△ABC中，
∠ADE=∠B，∠AED=∠C，∠A=∠A
=
=
=
∴DE∥BC，DE= BC。
∴△ADE∽△ABC
（相似三角形的定义）
E
D
C
B
A
已知,如图,D,E分别是△ABC的AB,AC边上的点, △ ADE∽△ABC.已知AD﹕DB=1﹕2,BC=9cm,求DE的长.
解：∵△ADE ∽△ABC
（相似三角形的对应边成比例）
∴DE=3（cm）
答：DE的长为3cm。
E
D
C
B
A
如图,D,E分别是△ABC的AB,AC边上的点△ADE∽△ABC,AE＝3cm,EB＝5cm,AC＝6cm,
求AD的长.
E
D
C
B
A
E
D
C
B
A
如图.△ACD∽△ABC, 且∠B＝ 40°，∠ADC ＝ 65°，
则 ① ∠ACD =＿＿ ；
　∠ACB = ＿＿ ；
40°
65°
DA
CD
AC
D
C
B
A
②
( ) ( ) ( )
＝
＝
AB
CA
BC
你说我说大家说
请你谈谈学习本节课后的感受!
1.相似三角形的定义:
对应角相等,对应边成比例的两个三角形,叫做相似三角形.
2.相似三角形性质：
相似三角形的对应角相等,对应边成比例.
3.相似三角形的三种基本图形
E
D
C
B
A
E
D
C
B
A
E
D
C
B
A
X型
A型
非A型
已知：如图，在Rt△ABC中，
∠ACB=Rt∠，AC=BC，CD⊥AB于点D。
求证：△ACD∽△ABC
A
D
C
B
证明：∵ ∠ACB=Rt∠， AC=BC， CD⊥AB
∴ ∠A =∠A， ∠ACD=∠B，∠ADC= ∠ACB，
∴ △ACD和△ACB是等腰直角三角形
∴ △ACD∽△ABC
　　　　　，　　　，　　　即
作业布置
必做题
1、作业本p26-27基础练习
2、课本p105作业题A组题
选做题
1、作业本p27综合运用
2、课本p105作业题B组题