第4章 平行四边形单元测试卷(含解析)
文档属性
| 名称 | 第4章 平行四边形单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 267.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 14:45:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版八年级数学下册单元测试卷
第四章
平行四边形
姓名:___________班级:___________学号:___________
一、选择题(本大题共10小题,共30.0分)
小斌家买了一套新房正在进行装修,星期天小斌陪父母一起到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设客厅地面需无缝,则购买的瓷砖形状不可以是
A.
三角形地砖
B.
正方形地砖
C.
正六边形地砖
D.
正五边形地砖
如图,在?ABCD中,,于点E,F为DC的中点,连结EF、BF,若,则
A.
B.
C.
D.
已知图形:等边三角形,平行四边形,菱形,圆.其中既是轴对称图形,又是中心对称图形的有
A.
1个
B.
2个
C.
3个
D.
4个
学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC、BD的中点重叠并用钉子固定,然后用木条将AB、BC、CD、DA分别钉起来.此时四边形ABCD即为平行四边形,这样做的依据是
A.
两组对边分别平行的四边形是平行四边形
B.
两组对边分别相等的四边形是平行四边形
C.
一组对边平行且相等的四边形是平行四边形
D.
对角线互相平分的四边形是平行四边形
如图,四边形ABCD中,,,,点M、N分别为线段BC、AB上的动点含端点,但点M不与点B重合,点E、F分别为DM、MN的中点,则EF长度的可能为
A.
2
B.
5
C.
7
D.
9
用反证法证明命题“三角形中必有一个内角小于或等于”时,首先应该假设这个三角形中
A.
??
有一个内角小于
B.
??
每一个内角都小于
C.
?
有一个内角大于
D.
?
每一个内角都大于
如图,在平行四边形ABCD中,,且,将沿AC翻折至,交CD于点E,连接若,则的长度为
A.
B.
C.
6
D.
9
已知点D与点,,是一平行四边形的四个顶点,则CD长的最小值为???
A.
B.
C.
13
D.
12
如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为若将横板AB换成横板,且,O仍为的中点,设点的最大高度为,则下列结论正确的是
A.
B.
C.
D.
?大小不确定
如图,在平行四边形ABCD中,,,点H、G分别是边AD、BC上的动点连接AH、HG,点E为AH的中点,点F为GH的中点,连接则EF的最大值与最小值的差为
A.
1
B.
C.
D.
二、填空题(本大题共8小题,共24.0分)
一个多边形的内角和与某一个外角的度数总和为,则这个多边形的边数是________。
已知平面直角坐标系内,,,,若以O,A,C,B为顶点的四边形是平行四边形,则点B不可能在第______象限.
用反证法证明“三角形的三个内角中,至少有一个大于或等于”时,应先假设?
?
?
?
?
??.
已知点D、E分别在的边BA、CA的延长线上,且,如果,,那么_________.
在?ABCD中,,,,对角线AC、BD交于点O,E为AD上一点,连接EO,若的周长比四边形ABOE的周长大3,则ED的长为______.
如图,直线EF经过?ABCD的对称中心O,且分别交AB、CD于E、若?ABCD的面积为,则图中阴影部分的面积为______.
如图,在梯形ABCD中,,,,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间______秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
如图,平行四边形钢板上有一圆洞,现需将该钢板阴影部分分成面积相等的两部分,如果限定只能用一条直线,能否做到:______选填“能”或“不能”若填“能”,请说明这条直线过哪两个点;若填“不能”,请简要说明理由:______.
三、解答题(本大题共6小题,共46.0分)
用反证法证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
如图,D是边BC的中点,连接AD并延长到点E,使,连接BE.
图中哪两个图形成中心对称?
若的面积为4,求的面积.
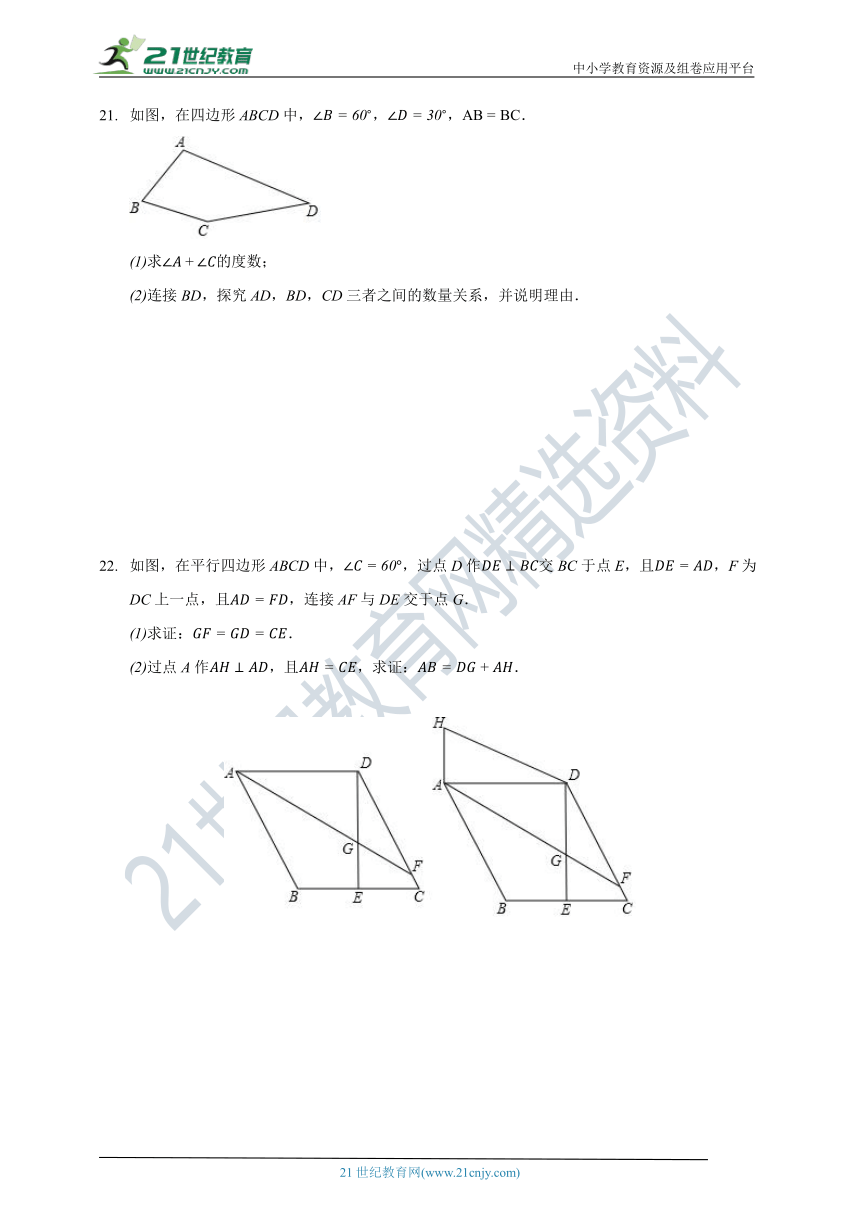
如图,在四边形ABCD中,,,.
求的度数;
连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由.
如图,在平行四边形ABCD中,,过点D作交BC于点E,且,F为DC上一点,且,连接AF与DE交于点G.
求证:.
过点A作,且,求证:.
如图,等腰直角和等腰直角,,,,P为AE的中点
连接PC,PD,则PC与PD的位置关系是________,数量关系是________,并证明你的结论;
当E在线段AB上变化时,其他条件不变,作于F,连接PF,试判断的形状;
在点E运动过程中,是否为等边三角形?若可以,试求与的两边之比.
如图,在矩形ABCD中,,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若,则,,,
当x为何值时,点P、N重合;
当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
答案和解析
1.【答案】D
解:A.正三角形的每个内角是,能整除,能用来铺设无缝地板;
B.正方形的每个内角是,能整除,能用来铺设无缝地板;
C.正六边形的每个内角是,能整除,能用来铺设无缝地板;
D.正五边形每个内角是,不能整除,不能用来铺设无缝地板;
故选D.
2.【答案】D
解:如图,延长EF、BC交于点G.
四边形ABCD是平行四边形,
,,
,
为DC中点,
,
在和中:
≌,
,
,
,
,
,
,
,
,
,
,
,
,
.
故选:D.
3.【答案】B
解:等边三角形,是轴对称图形,不是中心对称图形;
平行四边形,不是轴对称图形,是中心对称图形;
菱形,既是轴对称图形,又是中心对称图形;
圆,既是轴对称图形,也是中心对称图形;
综上可得,符合题意的有2个.
故选B.
4.【答案】D
解:将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.
得出,,则四边形ABCD就是平行四边形,
故这样做的依据是:对角线互相平分的四边形是平行四边形;
故选:D.
5.【答案】B
解:连接DN,
,,
,
最大时,EF最大,DN最小时,EF最小,
与B重合时DN最大,
此时,
的最大值为.
,,
,
,
长度的可能为5;
故选:B.
6.【答案】D
解:用反证法证明“三角形中必有一个内角小于或等于”时,
应先假设三角形中每一个内角都不小于或等于,即每一个内角都大于.
故选D.
7.【答案】C
解:作于M,如图所示:
由折叠的性质得:,,,
四边形ABCD是平行四边形,
,,,,
,
,
,,
,
,
在中,由勾股定理得:,
故选C.
8.【答案】A
解:有两种情况:
是平行四边形的一条边,那么有,
是平行四边形的一条对角线,
过C作于M,过D作于F,交AC于Q,过B作于N,
则,
,,
四边形ACBD是平行四边形,
,,,
,
,
在和中
≌,
,,
,
由勾股定理得:,当时,CD有最小值,是,
,
的最小值是.
故选A.
9.【答案】A
解:如图所示:
为AB的中点,,,
,
是的中位线,
,
同理,当将横板AB换成横板,且,O仍为的中点,设点的最大高度为,则,
.
故选A.
10.【答案】C
解:如图,取AD的中点M,连接CM、AG、AC,作于N.
四边形ABCD是平行四边形,,
,,
,
是等边三角形,
,,
,
,
,
在中,,,
,
,,
,
易知AG的最大值为AC的长,最小值为AN的长,
的最大值为,最小值为,
的最大值为,最小值为,
的最大值与最小值的差为.
故选C.
11.【答案】9
解:设这个多边形的边数为n,这个外角的度数为,
则,
由题意得:,
,
,
,
解之得:,
为正整数,
,
这个多边形的边数是9.
故答案为9.
12.【答案】三
解:连接A、O、C三点如下图示,得.
以任意两条边做平行四边形的两条边,分别作平行线,使其为平行四边形,
则得到的另一点就是点B,
由此可得B点不可能在第三象限.
故答案为:三.
13.【答案】三角形的三个内角都小于
解:用反证法证明“三角形的三个内角中,至少有一个大于或等于”时,应先假设三角形的三个内角都小于.
14.【答案】2
略
15.【答案】
解:,,,
,
,
四边形ABCD是平行四边形,
,
的周长比四边形ABOE的周长大3,
,
,
,
,
故答案为:.
16.【答案】2
解:是平行四边形的对称中心,
,,
的面积?ABCD的面积,
在≌中,
≌,
图中阴影部分的面积,
故答案为2.
17.【答案】2或
解:由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:
,
解得:,
当Q运动到E和C之间,设运动时间为t,则得:
,
解得:,
故答案为:2或.
18.【答案】能
?
对角线的交点和圆心
解:作一条过圆心与平行四边形对角线交点的直线即把该图形平分,如下图
故答案为:能;对角线的交点和圆心.
19.【答案】解:已知:如图,直线AB,CD被直线EF所截,.
求证:.
证明:假设直线AB与CD不平行,则AB与CD相交.
设AB,CD相交于点P,
得到,
则.
显然与相矛盾.
假设不成立.
.
20.【答案】解:图中和三角形EDB成中心对称;
和三角形EDB成中心对称,的面积为4,
的面积也为4,
为BC的中点,
的面积也为4,
所以的面积为8.
21.【答案】解:在四边形ABCD中,
,,,
,
故答案为:;
如图所示,
AD、BD、CD三者之间的等量关系为:.
理由如下:
连接BD,以BD为边向下作等边三角形,
则,,
,
,
在和中,,
≌,
,,
,
,
,
,,
.
22.【答案】证明:四边形ABD是平行四边形,
,,,
,,
,
,
,
,
,
,
,
,
,
,
在和中,,
≌,
,
;
证明:,,
,
在与中,,
≌,
,,,
四边形ABCD是平行四边形,
,,
,,
,
,
,
在DH上截取,如图所示:
,
,
,
,
,
在与中,,
≌,
,
,
.
23.【答案】解:,,
证明:
作于F,连接PF,作于H,
则四边形EFBD是正方形,
在和中,
,
≌,
,,
,P为AE的中点,
,又,
,,
,,
故答案为:;;
作于H,
则,P为AE的中点,
,又,
,
为等腰三角形;
设,,
是等边三角形,
,
,
∽,
,即,
解得,,
是梯形ACFE的中位线,
,
则与的两直角边之比为.
24.【答案】解:,N重合,
,
,舍去,
当时,P,N重合;
因为当N点到达A点时,,此时M点和Q点还未相遇,
所以点Q只能在点M的左侧,
当点P在点N的左侧时,依题意得
,
解得舍去,,
当时四边形PQMN是平行四边形;
当点P在点N的右侧时,依题意得
,
解得舍去,,
当时四边形NQMP是平行四边形,
所以当或时,以P,Q,M,N为顶点的四边形是平行四边形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
浙教版八年级数学下册单元测试卷
第四章
平行四边形
姓名:___________班级:___________学号:___________
一、选择题(本大题共10小题,共30.0分)
小斌家买了一套新房正在进行装修,星期天小斌陪父母一起到瓷砖商店去购买一种多边形形状的瓷砖,用来铺设客厅地面需无缝,则购买的瓷砖形状不可以是
A.
三角形地砖
B.
正方形地砖
C.
正六边形地砖
D.
正五边形地砖
如图,在?ABCD中,,于点E,F为DC的中点,连结EF、BF,若,则
A.
B.
C.
D.
已知图形:等边三角形,平行四边形,菱形,圆.其中既是轴对称图形,又是中心对称图形的有
A.
1个
B.
2个
C.
3个
D.
4个
学行四边形的相关知识后,小明采用下列方法钉制了一个平行四边形框架:如图,将两根木条AC、BD的中点重叠并用钉子固定,然后用木条将AB、BC、CD、DA分别钉起来.此时四边形ABCD即为平行四边形,这样做的依据是
A.
两组对边分别平行的四边形是平行四边形
B.
两组对边分别相等的四边形是平行四边形
C.
一组对边平行且相等的四边形是平行四边形
D.
对角线互相平分的四边形是平行四边形
如图,四边形ABCD中,,,,点M、N分别为线段BC、AB上的动点含端点,但点M不与点B重合,点E、F分别为DM、MN的中点,则EF长度的可能为
A.
2
B.
5
C.
7
D.
9
用反证法证明命题“三角形中必有一个内角小于或等于”时,首先应该假设这个三角形中
A.
??
有一个内角小于
B.
??
每一个内角都小于
C.
?
有一个内角大于
D.
?
每一个内角都大于
如图,在平行四边形ABCD中,,且,将沿AC翻折至,交CD于点E,连接若,则的长度为
A.
B.
C.
6
D.
9
已知点D与点,,是一平行四边形的四个顶点,则CD长的最小值为???
A.
B.
C.
13
D.
12
如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,设B点的最大高度为若将横板AB换成横板,且,O仍为的中点,设点的最大高度为,则下列结论正确的是
A.
B.
C.
D.
?大小不确定
如图,在平行四边形ABCD中,,,点H、G分别是边AD、BC上的动点连接AH、HG,点E为AH的中点,点F为GH的中点,连接则EF的最大值与最小值的差为
A.
1
B.
C.
D.
二、填空题(本大题共8小题,共24.0分)
一个多边形的内角和与某一个外角的度数总和为,则这个多边形的边数是________。
已知平面直角坐标系内,,,,若以O,A,C,B为顶点的四边形是平行四边形,则点B不可能在第______象限.
用反证法证明“三角形的三个内角中,至少有一个大于或等于”时,应先假设?
?
?
?
?
??.
已知点D、E分别在的边BA、CA的延长线上,且,如果,,那么_________.
在?ABCD中,,,,对角线AC、BD交于点O,E为AD上一点,连接EO,若的周长比四边形ABOE的周长大3,则ED的长为______.
如图,直线EF经过?ABCD的对称中心O,且分别交AB、CD于E、若?ABCD的面积为,则图中阴影部分的面积为______.
如图,在梯形ABCD中,,,,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间______秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
如图,平行四边形钢板上有一圆洞,现需将该钢板阴影部分分成面积相等的两部分,如果限定只能用一条直线,能否做到:______选填“能”或“不能”若填“能”,请说明这条直线过哪两个点;若填“不能”,请简要说明理由:______.
三、解答题(本大题共6小题,共46.0分)
用反证法证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
如图,D是边BC的中点,连接AD并延长到点E,使,连接BE.
图中哪两个图形成中心对称?
若的面积为4,求的面积.
如图,在四边形ABCD中,,,.
求的度数;
连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由.
如图,在平行四边形ABCD中,,过点D作交BC于点E,且,F为DC上一点,且,连接AF与DE交于点G.
求证:.
过点A作,且,求证:.
如图,等腰直角和等腰直角,,,,P为AE的中点
连接PC,PD,则PC与PD的位置关系是________,数量关系是________,并证明你的结论;
当E在线段AB上变化时,其他条件不变,作于F,连接PF,试判断的形状;
在点E运动过程中,是否为等边三角形?若可以,试求与的两边之比.
如图,在矩形ABCD中,,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若,则,,,
当x为何值时,点P、N重合;
当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
答案和解析
1.【答案】D
解:A.正三角形的每个内角是,能整除,能用来铺设无缝地板;
B.正方形的每个内角是,能整除,能用来铺设无缝地板;
C.正六边形的每个内角是,能整除,能用来铺设无缝地板;
D.正五边形每个内角是,不能整除,不能用来铺设无缝地板;
故选D.
2.【答案】D
解:如图,延长EF、BC交于点G.
四边形ABCD是平行四边形,
,,
,
为DC中点,
,
在和中:
≌,
,
,
,
,
,
,
,
,
,
,
,
,
.
故选:D.
3.【答案】B
解:等边三角形,是轴对称图形,不是中心对称图形;
平行四边形,不是轴对称图形,是中心对称图形;
菱形,既是轴对称图形,又是中心对称图形;
圆,既是轴对称图形,也是中心对称图形;
综上可得,符合题意的有2个.
故选B.
4.【答案】D
解:将两根木条AC、BD中点重叠,并用钉子固定,则四边形ABCD就是平行四边形.
得出,,则四边形ABCD就是平行四边形,
故这样做的依据是:对角线互相平分的四边形是平行四边形;
故选:D.
5.【答案】B
解:连接DN,
,,
,
最大时,EF最大,DN最小时,EF最小,
与B重合时DN最大,
此时,
的最大值为.
,,
,
,
长度的可能为5;
故选:B.
6.【答案】D
解:用反证法证明“三角形中必有一个内角小于或等于”时,
应先假设三角形中每一个内角都不小于或等于,即每一个内角都大于.
故选D.
7.【答案】C
解:作于M,如图所示:
由折叠的性质得:,,,
四边形ABCD是平行四边形,
,,,,
,
,
,,
,
,
在中,由勾股定理得:,
故选C.
8.【答案】A
解:有两种情况:
是平行四边形的一条边,那么有,
是平行四边形的一条对角线,
过C作于M,过D作于F,交AC于Q,过B作于N,
则,
,,
四边形ACBD是平行四边形,
,,,
,
,
在和中
≌,
,,
,
由勾股定理得:,当时,CD有最小值,是,
,
的最小值是.
故选A.
9.【答案】A
解:如图所示:
为AB的中点,,,
,
是的中位线,
,
同理,当将横板AB换成横板,且,O仍为的中点,设点的最大高度为,则,
.
故选A.
10.【答案】C
解:如图,取AD的中点M,连接CM、AG、AC,作于N.
四边形ABCD是平行四边形,,
,,
,
是等边三角形,
,,
,
,
,
在中,,,
,
,,
,
易知AG的最大值为AC的长,最小值为AN的长,
的最大值为,最小值为,
的最大值为,最小值为,
的最大值与最小值的差为.
故选C.
11.【答案】9
解:设这个多边形的边数为n,这个外角的度数为,
则,
由题意得:,
,
,
,
解之得:,
为正整数,
,
这个多边形的边数是9.
故答案为9.
12.【答案】三
解:连接A、O、C三点如下图示,得.
以任意两条边做平行四边形的两条边,分别作平行线,使其为平行四边形,
则得到的另一点就是点B,
由此可得B点不可能在第三象限.
故答案为:三.
13.【答案】三角形的三个内角都小于
解:用反证法证明“三角形的三个内角中,至少有一个大于或等于”时,应先假设三角形的三个内角都小于.
14.【答案】2
略
15.【答案】
解:,,,
,
,
四边形ABCD是平行四边形,
,
的周长比四边形ABOE的周长大3,
,
,
,
,
故答案为:.
16.【答案】2
解:是平行四边形的对称中心,
,,
的面积?ABCD的面积,
在≌中,
≌,
图中阴影部分的面积,
故答案为2.
17.【答案】2或
解:由已知梯形,
当Q运动到E和B之间,设运动时间为t,则得:
,
解得:,
当Q运动到E和C之间,设运动时间为t,则得:
,
解得:,
故答案为:2或.
18.【答案】能
?
对角线的交点和圆心
解:作一条过圆心与平行四边形对角线交点的直线即把该图形平分,如下图
故答案为:能;对角线的交点和圆心.
19.【答案】解:已知:如图,直线AB,CD被直线EF所截,.
求证:.
证明:假设直线AB与CD不平行,则AB与CD相交.
设AB,CD相交于点P,
得到,
则.
显然与相矛盾.
假设不成立.
.
20.【答案】解:图中和三角形EDB成中心对称;
和三角形EDB成中心对称,的面积为4,
的面积也为4,
为BC的中点,
的面积也为4,
所以的面积为8.
21.【答案】解:在四边形ABCD中,
,,,
,
故答案为:;
如图所示,
AD、BD、CD三者之间的等量关系为:.
理由如下:
连接BD,以BD为边向下作等边三角形,
则,,
,
,
在和中,,
≌,
,,
,
,
,
,,
.
22.【答案】证明:四边形ABD是平行四边形,
,,,
,,
,
,
,
,
,
,
,
,
,
,
在和中,,
≌,
,
;
证明:,,
,
在与中,,
≌,
,,,
四边形ABCD是平行四边形,
,,
,,
,
,
,
在DH上截取,如图所示:
,
,
,
,
,
在与中,,
≌,
,
,
.
23.【答案】解:,,
证明:
作于F,连接PF,作于H,
则四边形EFBD是正方形,
在和中,
,
≌,
,,
,P为AE的中点,
,又,
,,
,,
故答案为:;;
作于H,
则,P为AE的中点,
,又,
,
为等腰三角形;
设,,
是等边三角形,
,
,
∽,
,即,
解得,,
是梯形ACFE的中位线,
,
则与的两直角边之比为.
24.【答案】解:,N重合,
,
,舍去,
当时,P,N重合;
因为当N点到达A点时,,此时M点和Q点还未相遇,
所以点Q只能在点M的左侧,
当点P在点N的左侧时,依题意得
,
解得舍去,,
当时四边形PQMN是平行四边形;
当点P在点N的右侧时,依题意得
,
解得舍去,,
当时四边形NQMP是平行四边形,
所以当或时,以P,Q,M,N为顶点的四边形是平行四边形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
