浙教版数学八年级下册第四章 平行四边形›达标检测卷(含答案)
文档属性
| 名称 | 浙教版数学八年级下册第四章 平行四边形›达标检测卷(含答案) | 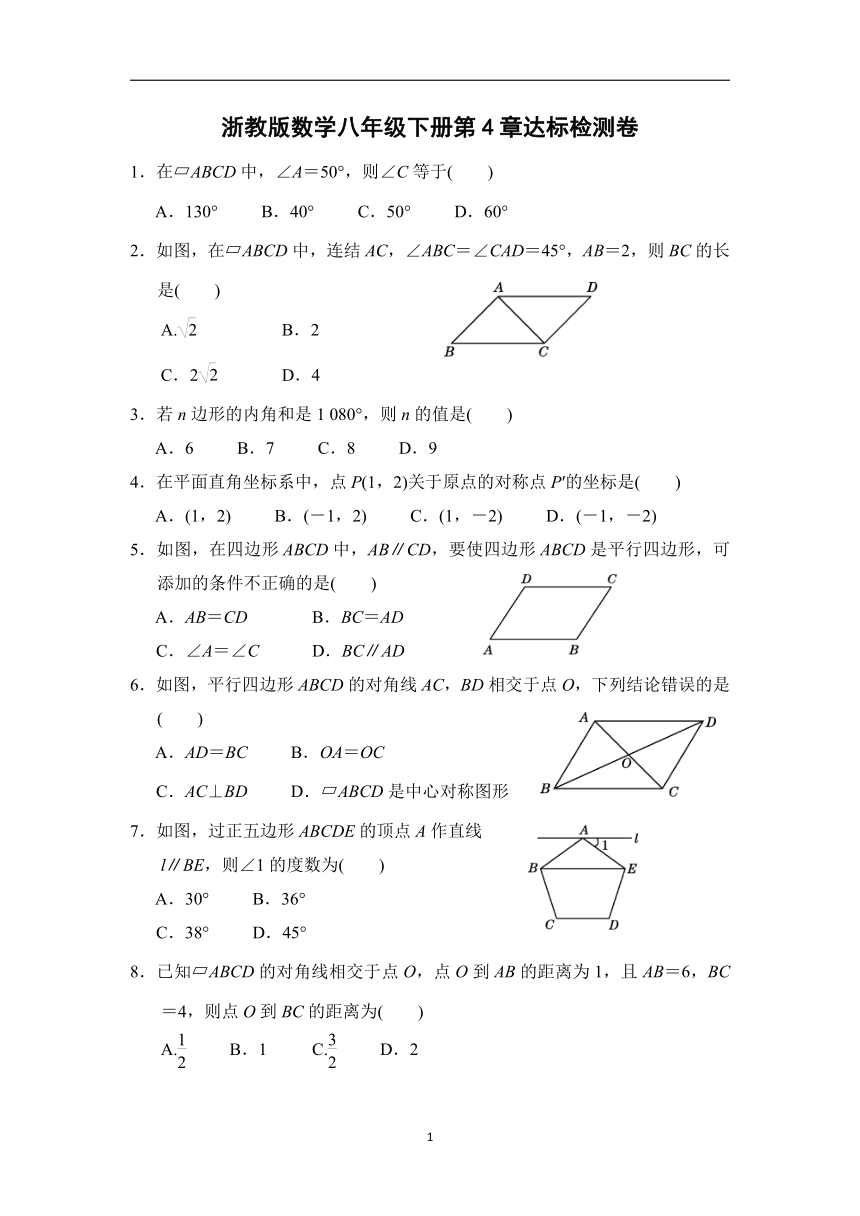 | |
| 格式 | doc | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-14 16:24:01 | ||
图片预览




文档简介
浙教版数学八年级下册第4章达标检测卷
1.在?ABCD中,∠A=50°,则∠C等于( )
A.130° B.40° C.50° D.60°
2.如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A. B.2
C.2 D.4
3.若n边形的内角和是1 080°,则n的值是( )
A.6 B.7 C.8 D.9
4.在平面直角坐标系中,点P(1,2)关于原点的对称点P′的坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
5.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC=AD
C.∠A=∠C D.BC∥AD
6.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( )
A.AD=BC B.OA=OC
C.AC⊥BD D.?ABCD是中心对称图形
7.如图,过正五边形ABCDE的顶点A作直线
l∥BE,则∠1的度数为( )
A.30° B.36°
C.38° D.45°
8.已知?ABCD的对角线相交于点O,点O到AB的距离为1,且AB=6,BC=4,则点O到BC的距离为( )
A. B.1 C. D.2
9.如图,在?ABCD中,延长AB到点E,使BE=AB,连结DE交BC于点F,则下列结论不一定成立的是( )
A.∠E=∠CDF B.EF=DF
C.AD=2BF D.BE=2CF
10.如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
A.70° B.40°
C.30° D.20°
二、填空题(本题有6小题,每小题4分,共24分)
11.已知一个多边形的每一个外角都等于60°,则这个多边形的边数是________.
12.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长为________.
13. 用反证法证明命题“不相等的角不是对顶角”时,应假设__________________.
14.如图,?ABCD的周长为36,对角线AC,BD相交于点O,E是CD的中点,BD=12,则△DOE的周长为________.
15.如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB=________.
16.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为________.
三、解答题(本题有7小题,共66分)
17.(8分)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△ADF≌△CBE;
(2)四边形ABCD是平行四边形.
18.(8分)在所给的9×9方格中,每个小正方形的边长都是1,按要求画平行四边形,使它的四个顶点以及对角线的交点都在方格的顶点上.
(1)在图甲中画一个平行四边形,使它的周长是整数;
(2)在图乙中画一个平行四边形,使它的周长不是整数.
19.(8分)如图,D,E分别是△ABC的边AB,AC的中点,点O是△ABC内部任意一点,连结OB,OC,点G,F分别是OB,OC的中点,顺次连结点D,G,F,E.求证:四边形DGFE是平行四边形.
20.(10分)如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证:
(1)AE=AF;
(2)BE=(AB+AC).
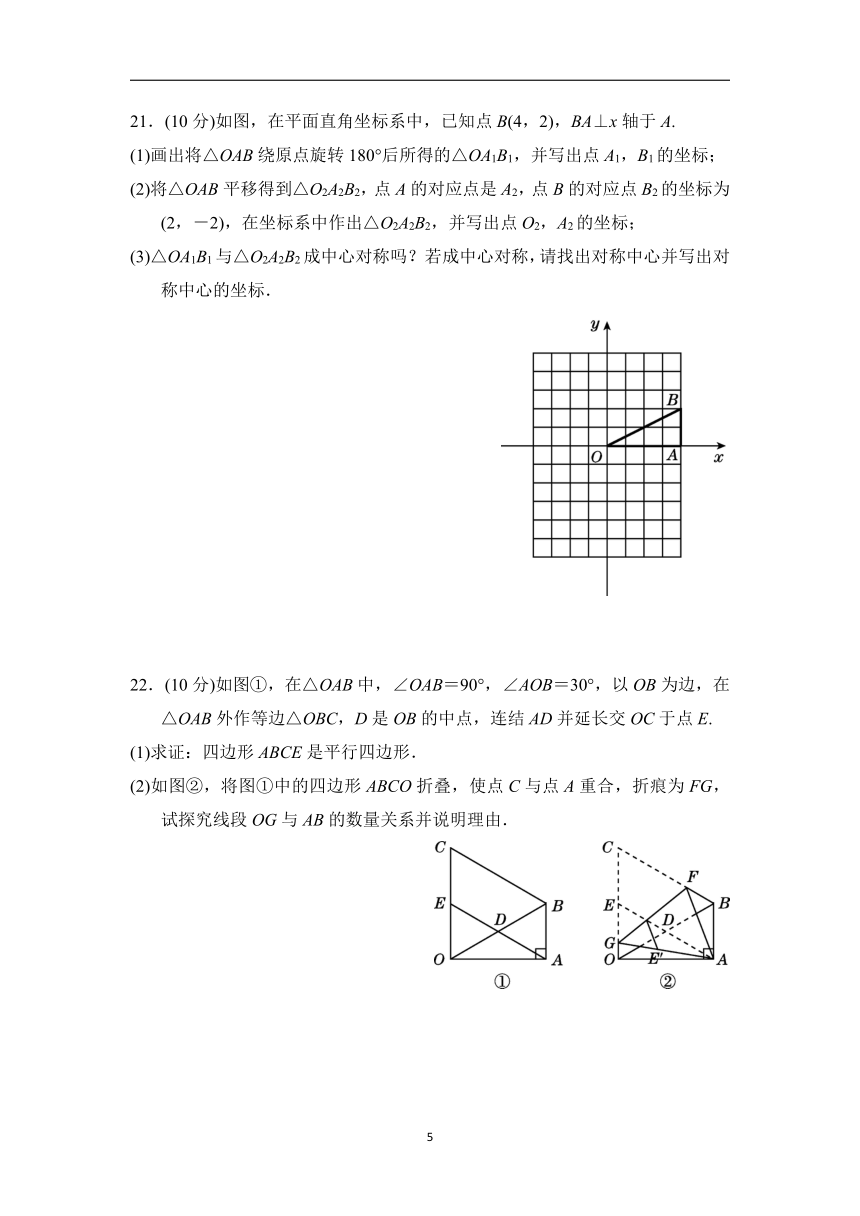
21.(10分)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2,点B的对应点B2的坐标为(2,-2),在坐标系中作出△O2A2B2,并写出点O2,A2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若成中心对称,请找出对称中心并写出对称中心的坐标.
22.(10分)如图①,在△OAB中,∠OAB=90°,∠AOB=30°,以OB为边,在△OAB外作等边△OBC,D是OB的中点,连结AD并延长交OC于点E.
(1)求证:四边形ABCE是平行四边形.
(2)如图②,将图①中的四边形ABCO折叠,使点C与点A重合,折痕为FG,试探究线段OG与AB的数量关系并说明理由.
23.(12分)如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连结AC,BD,CD,得平行四边形ABDC.
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连结MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标;
(3)若点P在直线BD上运动,连结PC,PO.请画出图形,直接写出∠CPO,∠DCP,∠BOP的数量关系.
答案
一、1.C 2.C 3.C 4.D 5.B 6.C 7.B
8.C 点拨:设O到BC的距离为x,易知S△OAB=S△OBC,∴×1×6=×x×4.解得x=,故选C.
9.D 10.B
二、11.6 12.20
13.不相等的角是对顶角
14.15 15.1
16. 点拨:连结BB′.根据已知条件和折叠的性质易知△BB′E是等腰直角三角形且∠BEB′=90°.因为BD=2,所以BE=1,所以BB′=.又因为BE=DE,B′E⊥BD,所以B′E是BD的中垂线,所以DB′=BB′=.
三、17.证明:(1)∵DF∥BE,
∴∠DFA=∠BEC.
在△ADF和△CBE中,
∴△ADF≌△CBE.
(2)∵△ADF≌△CBE,
∴AD=BC,∠DAF=∠BCE,
∴AD∥BC,
∴四边形ABCD是平行四边形.
18.解:如图所示.
(答案不唯一)
19.证明:∵D,E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC.
同理可得GF∥BC,且GF=BC,
∴DE∥GF且DE=GF,
∴四边形DEFG是平行四边形.
20.证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE.
∴∠AEF=∠AFE.
∴AE=AF.
(2)如图,过点C作CG∥EM,交BA的延长线于G,
易得∠G=∠AEF,∠ACG=∠AFE.
∵∠AEF=∠AFE,
∴∠G=∠ACG,∴AG=AC.
∵M为BC的中点,∴BM=CM.
∵EM∥CG,
∴BE=EG=BG=(BA+AG)=(AB+AC).
21.解:(1)如图,A1(-4,0),B1(-4,-2).
(2)如图,O2(-2,-4),A2(2,-4).
(3)成中心对称.如图,连结A1A2,OO2相交于点C,则对称中心为点C,其坐标为(-1,-2).
22.(1)证明:在Rt△OAB中,
∵D是OB的中点,∴DO=DA,
∴∠DAO=∠DOA=30°.
∵△OBC是等边三角形,
∴∠BCO=∠BOC=60°,
∴∠EOA=90°,∴∠AEO=60°,
∴∠BCO=∠AEO,∴BC∥AE.
∵∠EOA+∠BAO=90°+90°=180°,
∴AB∥OC,
∴四边形ABCE是平行四边形.
(2)解:OG=AB.理由如下:
在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,
∴BO=2AB,
∴OA==AB.
设OG=x,由折叠的性质可得AG=CG=OC-OG=OB-OG=2AB-x.
在Rt△OAG中,OG2+OA2=AG2,
∴x2+(AB)2=(2AB-x)2,
解得x=AB,即OG=AB.
23.解:(1)C(0,2),D(4,2).
(2)易知AB=4,CO=2,
则S平行四边形ABDC=AB·CO=4×2=8.
设点M的坐标为(0,m),
∴S△MAB=×4×|m|=2|m|,
∴2|m|=8,∴m=±4.
∴点M的坐标为(0,4)或(0,-4).
(3) 当点P在线段BD上时,如图①,
此时∠CPO=∠DCP+∠BOP;
当点P在线段BD的延长线上时,如图②,
此时∠CPO=∠BOP-∠DCP;
当点P在线段DB的延长线上时,如图③,
此时∠CPO=∠DCP-∠BOP.
1.在?ABCD中,∠A=50°,则∠C等于( )
A.130° B.40° C.50° D.60°
2.如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A. B.2
C.2 D.4
3.若n边形的内角和是1 080°,则n的值是( )
A.6 B.7 C.8 D.9
4.在平面直角坐标系中,点P(1,2)关于原点的对称点P′的坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
5.如图,在四边形ABCD中,AB∥CD,要使四边形ABCD是平行四边形,可添加的条件不正确的是( )
A.AB=CD B.BC=AD
C.∠A=∠C D.BC∥AD
6.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是( )
A.AD=BC B.OA=OC
C.AC⊥BD D.?ABCD是中心对称图形
7.如图,过正五边形ABCDE的顶点A作直线
l∥BE,则∠1的度数为( )
A.30° B.36°
C.38° D.45°
8.已知?ABCD的对角线相交于点O,点O到AB的距离为1,且AB=6,BC=4,则点O到BC的距离为( )
A. B.1 C. D.2
9.如图,在?ABCD中,延长AB到点E,使BE=AB,连结DE交BC于点F,则下列结论不一定成立的是( )
A.∠E=∠CDF B.EF=DF
C.AD=2BF D.BE=2CF
10.如图,在?ABCD中,∠A=70°,将?ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的直线上),折痕为MN,则∠AMF等于( )
A.70° B.40°
C.30° D.20°
二、填空题(本题有6小题,每小题4分,共24分)
11.已知一个多边形的每一个外角都等于60°,则这个多边形的边数是________.
12.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长为________.
13. 用反证法证明命题“不相等的角不是对顶角”时,应假设__________________.
14.如图,?ABCD的周长为36,对角线AC,BD相交于点O,E是CD的中点,BD=12,则△DOE的周长为________.
15.如图,在?ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB=________.
16.如图,在?ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为________.
三、解答题(本题有7小题,共66分)
17.(8分)如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:(1)△ADF≌△CBE;
(2)四边形ABCD是平行四边形.
18.(8分)在所给的9×9方格中,每个小正方形的边长都是1,按要求画平行四边形,使它的四个顶点以及对角线的交点都在方格的顶点上.
(1)在图甲中画一个平行四边形,使它的周长是整数;
(2)在图乙中画一个平行四边形,使它的周长不是整数.
19.(8分)如图,D,E分别是△ABC的边AB,AC的中点,点O是△ABC内部任意一点,连结OB,OC,点G,F分别是OB,OC的中点,顺次连结点D,G,F,E.求证:四边形DGFE是平行四边形.
20.(10分)如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.求证:
(1)AE=AF;
(2)BE=(AB+AC).
21.(10分)如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)画出将△OAB绕原点旋转180°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)将△OAB平移得到△O2A2B2,点A的对应点是A2,点B的对应点B2的坐标为(2,-2),在坐标系中作出△O2A2B2,并写出点O2,A2的坐标;
(3)△OA1B1与△O2A2B2成中心对称吗?若成中心对称,请找出对称中心并写出对称中心的坐标.
22.(10分)如图①,在△OAB中,∠OAB=90°,∠AOB=30°,以OB为边,在△OAB外作等边△OBC,D是OB的中点,连结AD并延长交OC于点E.
(1)求证:四边形ABCE是平行四边形.
(2)如图②,将图①中的四边形ABCO折叠,使点C与点A重合,折痕为FG,试探究线段OG与AB的数量关系并说明理由.
23.(12分)如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连结AC,BD,CD,得平行四边形ABDC.
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连结MA,MB,使S△MAB=S平行四边形ABDC,求出点M的坐标;
(3)若点P在直线BD上运动,连结PC,PO.请画出图形,直接写出∠CPO,∠DCP,∠BOP的数量关系.
答案
一、1.C 2.C 3.C 4.D 5.B 6.C 7.B
8.C 点拨:设O到BC的距离为x,易知S△OAB=S△OBC,∴×1×6=×x×4.解得x=,故选C.
9.D 10.B
二、11.6 12.20
13.不相等的角是对顶角
14.15 15.1
16. 点拨:连结BB′.根据已知条件和折叠的性质易知△BB′E是等腰直角三角形且∠BEB′=90°.因为BD=2,所以BE=1,所以BB′=.又因为BE=DE,B′E⊥BD,所以B′E是BD的中垂线,所以DB′=BB′=.
三、17.证明:(1)∵DF∥BE,
∴∠DFA=∠BEC.
在△ADF和△CBE中,
∴△ADF≌△CBE.
(2)∵△ADF≌△CBE,
∴AD=BC,∠DAF=∠BCE,
∴AD∥BC,
∴四边形ABCD是平行四边形.
18.解:如图所示.
(答案不唯一)
19.证明:∵D,E分别是AB,AC边的中点,
∴DE是△ABC的中位线,
∴DE∥BC,且DE=BC.
同理可得GF∥BC,且GF=BC,
∴DE∥GF且DE=GF,
∴四边形DEFG是平行四边形.
20.证明:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE.
∴∠AEF=∠AFE.
∴AE=AF.
(2)如图,过点C作CG∥EM,交BA的延长线于G,
易得∠G=∠AEF,∠ACG=∠AFE.
∵∠AEF=∠AFE,
∴∠G=∠ACG,∴AG=AC.
∵M为BC的中点,∴BM=CM.
∵EM∥CG,
∴BE=EG=BG=(BA+AG)=(AB+AC).
21.解:(1)如图,A1(-4,0),B1(-4,-2).
(2)如图,O2(-2,-4),A2(2,-4).
(3)成中心对称.如图,连结A1A2,OO2相交于点C,则对称中心为点C,其坐标为(-1,-2).
22.(1)证明:在Rt△OAB中,
∵D是OB的中点,∴DO=DA,
∴∠DAO=∠DOA=30°.
∵△OBC是等边三角形,
∴∠BCO=∠BOC=60°,
∴∠EOA=90°,∴∠AEO=60°,
∴∠BCO=∠AEO,∴BC∥AE.
∵∠EOA+∠BAO=90°+90°=180°,
∴AB∥OC,
∴四边形ABCE是平行四边形.
(2)解:OG=AB.理由如下:
在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,
∴BO=2AB,
∴OA==AB.
设OG=x,由折叠的性质可得AG=CG=OC-OG=OB-OG=2AB-x.
在Rt△OAG中,OG2+OA2=AG2,
∴x2+(AB)2=(2AB-x)2,
解得x=AB,即OG=AB.
23.解:(1)C(0,2),D(4,2).
(2)易知AB=4,CO=2,
则S平行四边形ABDC=AB·CO=4×2=8.
设点M的坐标为(0,m),
∴S△MAB=×4×|m|=2|m|,
∴2|m|=8,∴m=±4.
∴点M的坐标为(0,4)或(0,-4).
(3) 当点P在线段BD上时,如图①,
此时∠CPO=∠DCP+∠BOP;
当点P在线段BD的延长线上时,如图②,
此时∠CPO=∠BOP-∠DCP;
当点P在线段DB的延长线上时,如图③,
此时∠CPO=∠DCP-∠BOP.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
