数形结合思想在二次函数中的应用

(共14张PPT)
——数形结合思想在
　　　　二次函数问题中的应用
7
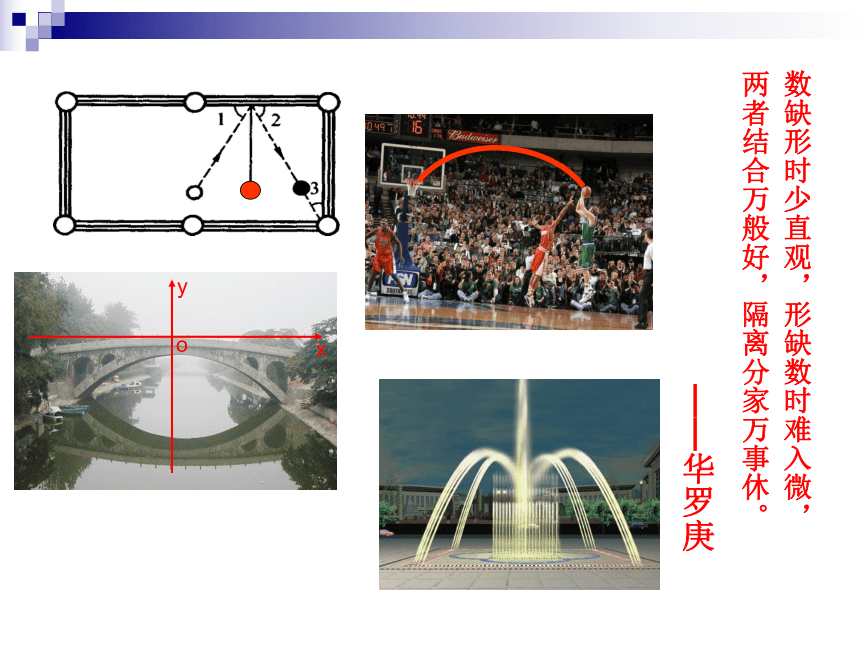
两者结合万般好，隔离分家万事休。
数缺形时少直观，形缺数时难入微，
——华罗庚
x
y
o
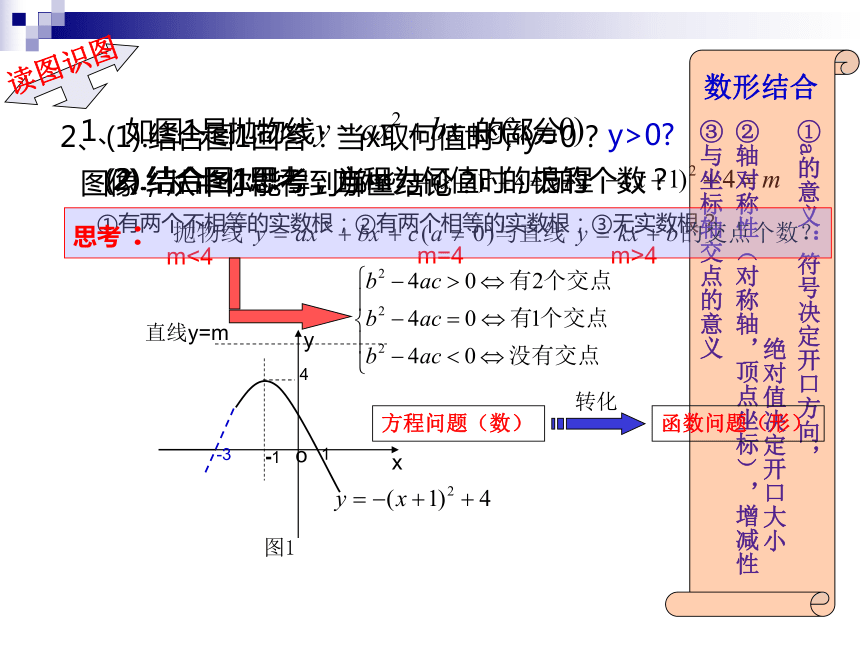
1、如图1是抛物线 的部分
图像，从中你能得到哪些结论？
2、(1).结合图1回答：当x取何值时，y=0？
y>0
(2).结合图1思考，当m为何值时，方程
①有两个不相等的实数根；②有两个相等的实数根；③无实数根？
①a的意义：符号决定开口方向，
绝对值决定开口大小
②轴对称性（对称轴，顶点坐标），增减性
③与坐标轴交点的意义
数形结合
方程问题（数）
函数问题（形）
转化
读图识图
x
y
o
4
-1
图1
1
-3
直线y=m
m<4
m=4
m>4
思考：
(2).结合图1思考，方程 的根的个数？
A
B
x
y
o
4
-1
图2
1
不等式问题（数）
函数问题（形）
转化
读图识图
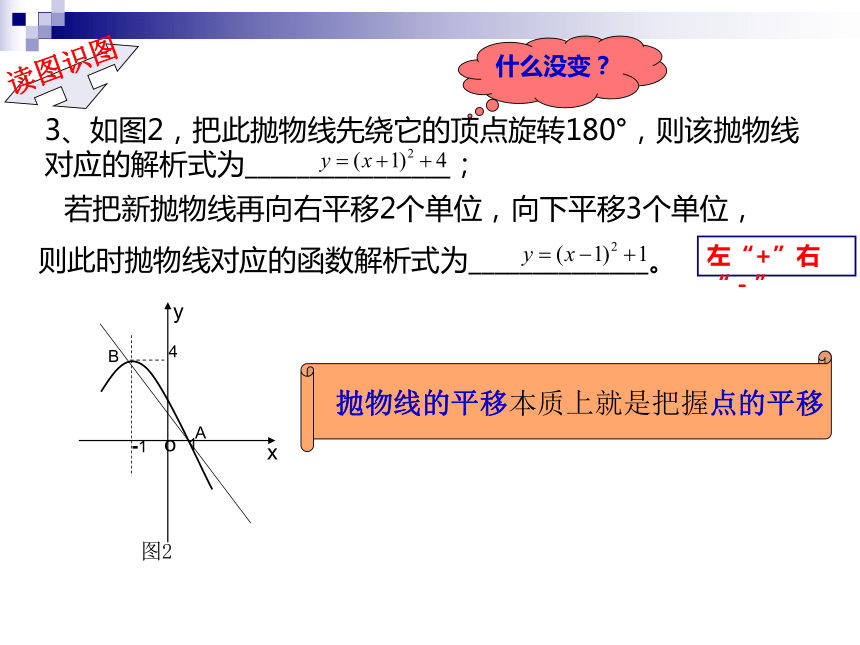
3、如图2，把此抛物线先绕它的顶点旋转180°，则该抛物线对应的解析式为________________；
若把新抛物线再向右平移2个单位，向下平移3个单位，
则此时抛物线对应的函数解析式为______________。
A
B
x
y
o
4
-1
图2
1
抛物线的平移本质上就是把握点的平移
读图识图
什么没变？
左“+”右“－”
巩固深化
x
y
1
数形结合
利用函数对称性：
观察点到对称轴的距离与函数值大小的关系
<
<
巩固深化
①
③
②
A. 只有①②
B. 只有①③
C. 只有②③
D. 都对
方程、不等式（数）
函数问题（形）
转化
数 形 结 合
B
应用思考
例：按右图所示的流程，输入一个数据x,根据y与x的关系式就输出一个数据y，这样可以将一组数据变成另一组数据，要使任意一组都在20~100（含20和100）之间的数据，变换成一组新数据后能满足下列两个要求：
(Ⅰ)新数据都在60~100（含60和100）之间；
(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致，即原数据大的对应的新数据也较大。
若关系式y=a(x-h)2+k(a>0)将数据进行变换，请写出一个满足上述要求的这种关系式。
开始
输入x
Y与x的关系式
输出y
结束
变式一：若将关系式y=a(x-h)2+k中的a>0改为a<0，关系式又将怎样？
变式二：若将(Ⅱ)新数据之间的大小关系与原数据之间的大小关系一致改为相反，即原数据越大的对应的新数据越小呢？
分享收获
一双慧眼——数与形
一个核心
数形结合思想（用数表达，用形释义）；
二项性质
四点注意
三种表达
轴对称性，增减性；
一般式，顶点式，交点式；
（1）a决定了抛物线的开口方向与大小；
（2）抛物线的平移要抓住点的平移规律；
（3）二次函数值大小可以直接通过开口方向与点到对称的轴距离确定；
（4）方程、不等式问题（数） 函数问题（形）