2020-2021学年浙教版八年级上册2.7勾股定理专题培优(Word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级上册2.7勾股定理专题培优(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 792.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 13:45:04 | ||
图片预览



文档简介
2020-2021学年浙教版八年级上册勾股定理专题培优
姓名
班级
学号
基础巩固
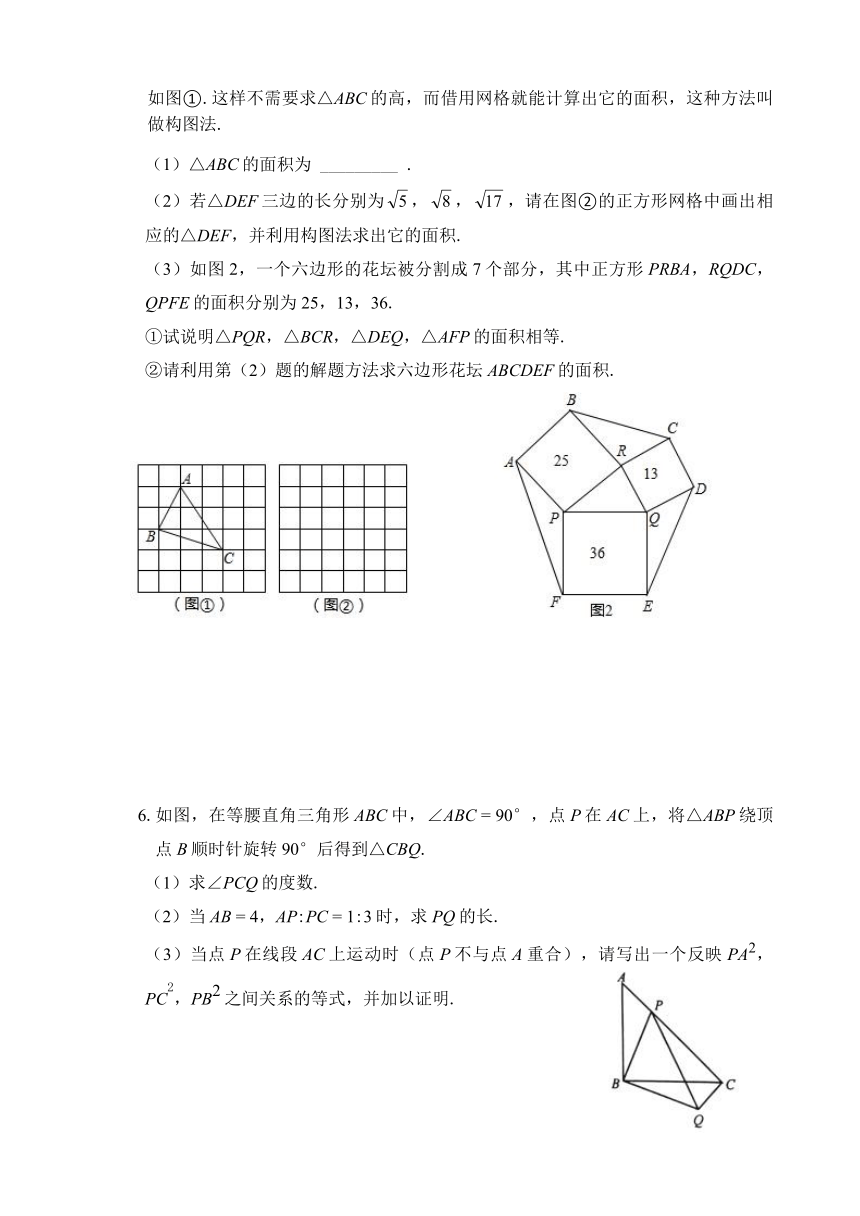
1.如图,在△ABC中,AB
=
AC
=
5,BC
=
8,D是线段BC上的动点(不含端点B,C).若线段AD的长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
第1题
第2题
第3题
2.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图的长方形由两个这样的图形拼成,若a
=
3,b
=
4,则该长方形的面积为( ).
A.20
B.24
C.
D.
3.把两块同样大小的含45°角的三角尺按如图的方式放置,其中一块三角尺的锐角顶点与另一块三角尺的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上,若AB
=
3,则CD
=
_________
.
4.我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图1.如图2,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为
_________
.
5.在△ABC中,AB,BC,AC三边的长分别为,,,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①.这样不需要求△ABC的高,而借用网格就能计算出它的面积,这种方法叫做构图法.
(1)△ABC的面积为
_________
.
(2)若△DEF三边的长分别为,,,请在图②的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
(3)如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为25,13,36.
①试说明△PQR,△BCR,△DEQ,△AFP的面积相等.
②请利用第(2)题的解题方法求六边形花坛ABCDEF的面积.
6.如图,在等腰直角三角形ABC中,∠ABC
=
90°,点P在AC上,将△ABP绕顶点B顺时针旋转90°后得到△CBQ.
(1)求∠PCQ的度数.
(2)当AB
=
4,AP:PC
=
1:3时,求PQ的长.
(3)当点P在线段AC上运动时(点P不与点A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
拓展提优
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab
=
8,大正方形的面积为25,则小正方形的边长为( ).
A.9
B.6
C.4
D.3
2.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C落在边AB上,连结BC.若∠ACB
=
∠ACB′
=
90°,AC
=
BC
=
3,则B′C的长为( ).
A.3
B.6
C.3
D.
3.如图,在△ABC中,AB
=
6,AC
=
9,AD⊥BC于点D,M为AD上任一点,则MC2
-
MB2
=
_________
.
4.如图,在△ABC中,AB
=
BC
=
8,AO
=
BO,点M是射线CO上的一个动点,∠AOC
=
60°,则当△ABM为直角三角形时,AM的长为
_________
.
5.在△ABC中,AB
=
15,BC
=
14,AC
=
13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
6.如图,在Rt△ABC中,∠B
=
30°,∠ACB
=
90°,CD⊥AB交AB于点D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E
=
30°,∠DCE
=
90°,再用同样的方法作Rt△FGC,∠FCG
=
90°,继续用同样的方法作Rt△HIC,∠HCI
=
90°.若AC
=
a,求CI的长.
冲刺重高
1.如图,已知∠B
=
∠C
=
∠D
=
∠E
=
90°,且AB
=
CD
=
3,BC
=
4,DE
=
EF
=
2,则A,F两点间的距离是( ).
A.14
B.6
+
C.8
+
D.10
2.如图,在四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC
=
30°,AD
=
6,BD
=
10,则CD
=
_________
.
3.如图是小章为学校举办的数学文化节设计的标志,在△ABC中,∠ACB
=
90°,以△ABC的各边为边作三个正方形,点G落在HI上.若AC
+
BC
=
6,空白部分的面积为10.5,则阴影部分的面积为
_________
.
4.已知在△ABC中,AB
=
AC.
(1)如图1,在△ADE中,若AD
=
AE,且∠DAE
=
∠BAC,求证:CD
=
BE.
(2)如图2,在△ADE中,若∠DAE
=
∠BAC
=
60°,且CD垂直平分AE,AD
=
3,CD
=
4,求BD的长.
(3)如图3,在△ADE中,当BD垂直平分AE于H,且∠BAC
=
2∠ADB时,试探究CD2,BD2,AF2之间的数量关系,并证明.
姓名
班级
学号
基础巩固
1.如图,在△ABC中,AB
=
AC
=
5,BC
=
8,D是线段BC上的动点(不含端点B,C).若线段AD的长为正整数,则点D的个数共有( )
A.5个
B.4个
C.3个
D.2个
第1题
第2题
第3题
2.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图的长方形由两个这样的图形拼成,若a
=
3,b
=
4,则该长方形的面积为( ).
A.20
B.24
C.
D.
3.把两块同样大小的含45°角的三角尺按如图的方式放置,其中一块三角尺的锐角顶点与另一块三角尺的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上,若AB
=
3,则CD
=
_________
.
4.我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图1.如图2,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为
_________
.
5.在△ABC中,AB,BC,AC三边的长分别为,,,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①.这样不需要求△ABC的高,而借用网格就能计算出它的面积,这种方法叫做构图法.
(1)△ABC的面积为
_________
.
(2)若△DEF三边的长分别为,,,请在图②的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
(3)如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为25,13,36.
①试说明△PQR,△BCR,△DEQ,△AFP的面积相等.
②请利用第(2)题的解题方法求六边形花坛ABCDEF的面积.
6.如图,在等腰直角三角形ABC中,∠ABC
=
90°,点P在AC上,将△ABP绕顶点B顺时针旋转90°后得到△CBQ.
(1)求∠PCQ的度数.
(2)当AB
=
4,AP:PC
=
1:3时,求PQ的长.
(3)当点P在线段AC上运动时(点P不与点A重合),请写出一个反映PA2,PC2,PB2之间关系的等式,并加以证明.
拓展提优
1.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab
=
8,大正方形的面积为25,则小正方形的边长为( ).
A.9
B.6
C.4
D.3
2.如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C落在边AB上,连结BC.若∠ACB
=
∠ACB′
=
90°,AC
=
BC
=
3,则B′C的长为( ).
A.3
B.6
C.3
D.
3.如图,在△ABC中,AB
=
6,AC
=
9,AD⊥BC于点D,M为AD上任一点,则MC2
-
MB2
=
_________
.
4.如图,在△ABC中,AB
=
BC
=
8,AO
=
BO,点M是射线CO上的一个动点,∠AOC
=
60°,则当△ABM为直角三角形时,AM的长为
_________
.
5.在△ABC中,AB
=
15,BC
=
14,AC
=
13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
6.如图,在Rt△ABC中,∠B
=
30°,∠ACB
=
90°,CD⊥AB交AB于点D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E
=
30°,∠DCE
=
90°,再用同样的方法作Rt△FGC,∠FCG
=
90°,继续用同样的方法作Rt△HIC,∠HCI
=
90°.若AC
=
a,求CI的长.
冲刺重高
1.如图,已知∠B
=
∠C
=
∠D
=
∠E
=
90°,且AB
=
CD
=
3,BC
=
4,DE
=
EF
=
2,则A,F两点间的距离是( ).
A.14
B.6
+
C.8
+
D.10
2.如图,在四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.∠ADC
=
30°,AD
=
6,BD
=
10,则CD
=
_________
.
3.如图是小章为学校举办的数学文化节设计的标志,在△ABC中,∠ACB
=
90°,以△ABC的各边为边作三个正方形,点G落在HI上.若AC
+
BC
=
6,空白部分的面积为10.5,则阴影部分的面积为
_________
.
4.已知在△ABC中,AB
=
AC.
(1)如图1,在△ADE中,若AD
=
AE,且∠DAE
=
∠BAC,求证:CD
=
BE.
(2)如图2,在△ADE中,若∠DAE
=
∠BAC
=
60°,且CD垂直平分AE,AD
=
3,CD
=
4,求BD的长.
(3)如图3,在△ADE中,当BD垂直平分AE于H,且∠BAC
=
2∠ADB时,试探究CD2,BD2,AF2之间的数量关系,并证明.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
