1.2.1 二次函数的图像同步培优练习(含解析)
文档属性
| 名称 | 1.2.1 二次函数的图像同步培优练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题1.2二次函数的图象(1)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共25题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)函数y=ax2﹣1与y=ax(a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
2.(2019秋?长春期末)二次函数y=(x+1)2﹣2的图象大致是( )
A. B.
C. D.
3.(2019秋?巴彦县期末)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
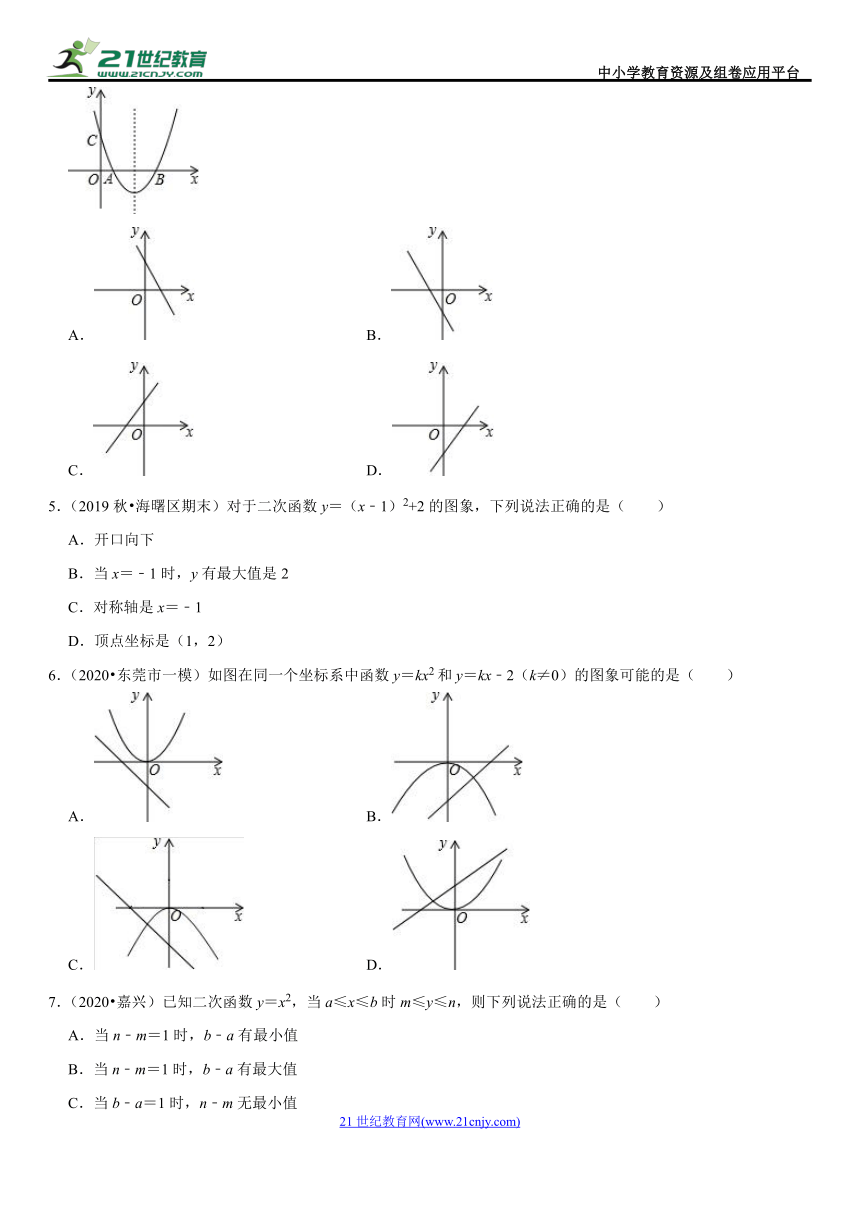
4.(2020?南宁一模)如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A. B.
C. D.
5.(2019秋?海曙区期末)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下
B.当x=﹣1时,y有最大值是2
C.对称轴是x=﹣1
D.顶点坐标是(1,2)
6.(2020?东莞市一模)如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
7.(2020?嘉兴)已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
8.(2020?宁波模拟)已知点P(m,n)在抛物线y=a(x﹣5)2+9(a≠0)上,当3<m<4时,总有n>1,当7<m<8时,总有n<1,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
9.(2020?永嘉县模拟)已知抛物线y=a(x﹣2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2,则m的取值范围是( )
A.0<m<1 B.0<m<2 C.1<m<2 D.m<2
10.(2020?雁塔区校级一模)已知抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,则下列说法正确的是( )
A.a>0
B.h<0
C.k≥3
D.当x<0时,y随x的增大而增大
二.填空题(共8小题)
11.(2020?哈尔滨)抛物线y=3(x﹣1)2+8的顶点坐标为 .
12.(2020?黄岩区模拟)二次函数y=x2﹣1图象的顶点坐标是 .
13.(2020?三门县一模)已知函数y,在自变量x≤m的范围内,相应的函数最小值为0,则m的取值范围是 .
14.(2020春?武邑县校级月考)若函数y,则当函数值y=12时,自变量x的值是 .
15.(2020?奉贤区一模)如果二次函数y=a(x﹣1)2(a≠0)的图象在它的对称轴右侧部分是上升的,那么a的取值范围是 .
16.(2019秋?溧阳市期末)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第 象限.
17.(2018秋?城厢区月考)如图所示四个二次函数的图象中,分别对应的是:①y=a1x2;②y=a2x2;③y=a3x2;则a1、a2、a3的大小关系是 .
18.(2018秋?顺河区校级月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=﹣2x2的图象,则阴影部分的面积是 .
三.解答题(共7小题)
19.(2020?拱墅区模拟)在同一直角坐标系中画出二次函数yx2+1与二次函数yx2﹣1的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
20.(2019秋?南昌县期中)已知点(3,13)在函数y=ax2+b的图象上,当x=﹣2时,y=8.
(1)求a,b的值;
(2)如果点(6,m),(n,20)也在这个函数的图象上,求m与n的值.
21.(2019秋?衢州期中)已知二次函数的表达式为y=﹣3(x﹣3)2+2.
(1)写出该函数的顶点坐标;
(2)判断点(1,﹣12)是否在这个函数的图象上.
22.(2019秋?萧山区期中)已知二次函数y(x﹣1)2
(1)完成下表;
x … …
y … …
(2)在如图的坐标系中描点,画出该二次函数的图象.
23.(2019秋?丹江口市期中)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A,B两点,
(1)求A,B两点的坐标.
(2)求△ABO的面积.
24.(2019秋?思明区校级期中)已知二次函数y=x2+k的图象经过点(﹣2,3)
(1)求二次函数的解析式;
(2)画出此二次函数的图象.
25.(2019秋?包河区期中)抛物线y=a(x+h)2的顶点为(2,0),它的形状与y=3x2相同,但开口方向与之相反.
(1)直接写出抛物线的解析式;
(2)求抛物线与y轴的交点坐
专题1.2二次函数的图象(1)解析版
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)函数y=ax2﹣1与y=ax(a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
【分析】本题可先抛物线与y轴的交点排除C、D,然后根据一次函数y=ax图象得到a的正负,再与二次函数y=ax2的图象相比较看是否一致.
【解析】由函数y=ax2﹣1可知抛物线与y轴交于点(0,﹣1),故C、D错误;
A、由抛物线可知,a>0,由直线可知,a<0,故A错误;
B、由抛物线可知,a>0,由直线可知,a>0,故B正确;
故选:B.
2.(2019秋?长春期末)二次函数y=(x+1)2﹣2的图象大致是( )
A.B. C.D.
【分析】分别根据抛物线的开口方向、对称轴的位置及抛物线与y轴的交点位置逐一判断可得.
【解析】在y=(x+1)2﹣2中由a=1>0知抛物线的开口向上,故A错误;
其对称轴为直线x=﹣1,在y轴的左侧,故B错误;
由y=(x+1)2﹣2=x2+2x﹣1知抛物线与y轴的交点为(0,﹣1),在y轴的负半轴,故D错误;
故选:C.
3.(2019秋?巴彦县期末)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
【分析】根据一次函数和二次函数的图象得出a、b的范围,看看是否相同且ab>0即可.
【解析】A、根据一次函数得出a<0,b>0,根据二次函数得出a>0,则ab<0,故本选项错误;
B、根据一次函数得出a>0,b<0,根据二次函数得出a>0,则ab<0,故本选项错误;
C、根据一次函数得出a<0,b<0,根据二次函数得出a<0,则ab>0,故本选项正确;
D、根据一次函数得出a<0,b>0,根据二次函数得出a<0,则ab<0,故本选项错误;
故选:C.
4.(2020?南宁一模)如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A. B.
C. D.
【分析】根据函数图象与y轴的交点,可得m>0,根据二次函数图象当x=a时,y<0,可得a>0,a﹣1<0,根据一次函数的性质,可得答案.
【解析】把x=a代入函数y=x2﹣x+m,得y=a2﹣a+m=a(a﹣1)+m,
∵x=a时,y<0,即 a(a﹣1)+m<0.
由图象交y轴的正半轴于点C,得m>0,
即a(a﹣1)<0.
x=a时,y<0,∴a>0,a﹣1<0,
∴一次函数y=(a﹣1)x+m的图象过一二四象限,
故选:A.
5.(2019秋?海曙区期末)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下
B.当x=﹣1时,y有最大值是2
C.对称轴是x=﹣1
D.顶点坐标是(1,2)
【分析】根据二次函数的性质对各选项进行判断.
【解析】二次函数y=(x﹣1)2+2的图象的开口向上,故A错误;
当x=1时,函数有最小值2,故B错误;
对称轴为直线x=1,故C错误;
顶点坐标为(1,2),故D正确.
故选:D.
6.(2020?东莞市一模)如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
【解析】当k>0时,函数y=kx﹣2的图象经过一、三、四象限;函数y=kx2的开口向上,对称轴在y轴上;
当k<0时,函数y=kx﹣2的图象经过二、三、四象限;函数y=kx2的开口向下,对称轴在y轴上,故C正确.
故选:C.
7.(2020?嘉兴)已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
【分析】方法1、①当b﹣a=1时,当a,b同号时,先判断出四边形BCDE是矩形,得出BC=DE=b﹣a=1,CD=BE=m,进而得出AC=n﹣m,即tan∠ABC=n﹣m,再判断出45°≤∠ABC<90°,即可得出n﹣m的范围,当a,b异号时,m=0,当a,b时,n最小,即可得出n﹣m的范围;
②当n﹣m=1时,当a,b同号时,同①的方法得出NH=PQ=b﹣a,HQ=PN=m,进而得出MH=n﹣m=1,而tan∠MHN,再判断出45°≤∠MNH<90°,当a,b异号时,m=0,则n=1,即可求出a,b,即可得出结论.
方法2、根据抛物线的性质判断,即可得出结论.
【解析】方法1、①当b﹣a=1时,当a,b同号时,如图1,
过点B作BC⊥AD于C,
∴∠BCD=90°,
∵∠ADE=∠BED=90°,
∴∠ADD=∠BCD=∠BED=90°,
∴四边形BCDE是矩形,
∴BC=DE=b﹣a=1,CD=BE=m,
∴AC=AD﹣CD=n﹣m,
在Rt△ACB中,tan∠ABCn﹣m,
∵点A,B在抛物线y=x2上,且a,b同号,
∴45°≤∠ABC<90°,
∴tan∠ABC≥1,
∴n﹣m≥1,
当a,b异号时,m=0,
当a,b时,n,此时,n﹣m,
∴n﹣m<1,
即n﹣m,
即n﹣m无最大值,有最小值,最小值为,故选项C,D都错误;
②当n﹣m=1时,如图2,
当a,b同号时,过点N作NH⊥MQ于H,
同①的方法得,NH=PQ=b﹣a,HQ=PN=m,
∴MH=MQ﹣HQ=n﹣m=1,
在Rt△MHN中,tan∠MNH,
∵点M,N在抛物线y=x2上,
∴m≥0,
当m=0时,n=1,
∴点N(0,0),M(1,1),
∴NH=1,
此时,∠MNH=45°,
∴45°≤∠MNH<90°,
∴tan∠MNH≥1,
∴1,
当a,b异号时,m=0,
∴n=1,
∴a=﹣1,b=1,
即b﹣a=2,
∴b﹣a无最小值,有最大值,最大值为2,故选项A错误;
故选:B.
方法2、当n﹣m=1时,
当a,b在y轴同侧时,a,b都越大时,a﹣b越接近于0,但不能取0,即b﹣a没有最小值,
当a,b异号时,当a=﹣1,b=1时,b﹣a=2最大,
当b﹣a=1时,当a,b在y轴同侧时,a,b离y轴越远,n﹣m越大,但取不到最大,
当a,b在y轴两侧时,当a,b时,n﹣m取到最小,最小值为,
因此,只有选项B正确,
故选:B.
8.(2020?宁波模拟)已知点P(m,n)在抛物线y=a(x﹣5)2+9(a≠0)上,当3<m<4时,总有n>1,当7<m<8时,总有n<1,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
【分析】依解析式可知顶点坐标,根据当7<m<8时,总有n<1,可知a<0,由增减性可列不等式组,解出即可.
【解析】∵抛物线y=a(x﹣5)2+9(a≠0),
∴抛物线的顶点为(5,9),
∵当7<m<8时,总有n<1,
∴a不可能大于0,
则a<0,
∴x<5时,y随x的增大而增大,x>5时,y随x的增大而减小,
∵当3<m<4时,总有n>1,当7<m<8时,总有n<1,且x=3与x=7对称,
∴m=3时,n≤1,m=7时,n≥1,
∴,
∴4a+9=1,
∴a=﹣2,
故选:D.
9.(2020?永嘉县模拟)已知抛物线y=a(x﹣2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2,则m的取值范围是( )
A.0<m<1 B.0<m<2 C.1<m<2 D.m<2
【分析】根据题目中的抛物线,可以得到该抛物线的对称轴,然后根据题意,可知点A和点B在对称轴两侧,从而可以得到m的取值范围,本题得以解决.
【解析】∵抛物线y=a(x﹣2)2+1,
∴该抛物线的对称轴为直线x=2,
∵点A(m,y1),B(m+2,y2)在抛物线y=a(x﹣2)2+1上,点A在抛物线对称轴的左侧,且1<y1<y2,
∴1<m<2,
故选:C.
10.(2020?雁塔区校级一模)已知抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,则下列说法正确的是( )
A.a>0
B.h<0
C.k≥3
D.当x<0时,y随x的增大而增大
【分析】利用对称性得到抛物线对称轴为直线x=1,根据点的坐标确定开口向下,最大值大于3,根据二次函数的性质即可判断D正确.
【解析】∵抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,
∴抛物线的开口向下,对称轴为直线x1,即a<0,h=1,
∴k>3,当x<1时,y随x的增大而增大,
故选:D.
二.填空题(共8小题)
11.(2020?哈尔滨)抛物线y=3(x﹣1)2+8的顶点坐标为 (1,8) .
【分析】已知抛物线顶点式y=a(x﹣h)2+k,顶点坐标是(h,k).
【解析】∵抛物线y=3(x﹣1)2+8是顶点式,
∴顶点坐标是(1,8).
故答案为:(1,8).
12.(2020?黄岩区模拟)二次函数y=x2﹣1图象的顶点坐标是 (0,﹣1) .
【分析】根据二次函数的性质,利用顶点式直接得出顶点坐标即可.
【解析】二次函数y=x2﹣1图象的顶点坐标是:(0,﹣1).
故答案为:(0,﹣1).
13.(2020?三门县一模)已知函数y,在自变量x≤m的范围内,相应的函数最小值为0,则m的取值范围是 1≤m≤3 .
【分析】画出函数的图象,根据函数的图象即可求得.
【解析】画出函数y的图象如图:
在自变量x≤m的范围内,相应的函数最小值为0,由图象可知:m的取值范围是1≤m≤3,
故答案为1≤m≤3.
14.(2020春?武邑县校级月考)若函数y,则当函数值y=12时,自变量x的值是 6或 .
【分析】根据函数y,分两种两种情况,令y=12代入分别求得相应的x的值,本题得以解决.
【解析】∵函数y,
∴当x≤2时,令x2+2=12,得x,
当x>2时,令2x=12,得x=6,
故答案为:6或.
15.(2020?奉贤区一模)如果二次函数y=a(x﹣1)2(a≠0)的图象在它的对称轴右侧部分是上升的,那么a的取值范围是 a>0 .
【分析】由于二次函数的图象在对称轴x=2的右侧部分是上升的,由此可以确定二次函数的二次项系数为正数.
【解析】∵二次函数的图象在对称轴x=1的右侧部分是上升的,
∴这个二次函数的二次项系数为正数,
∴a>0,
故答案为a>0.
16.(2019秋?溧阳市期末)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第 一 象限.
【分析】由二次函数解析式表示出顶点坐标,根据图形得到顶点在第四象限,求出m与n的正负,即可作出判断.
【解析】根据题意得:抛物线的顶点坐标为(﹣m,n),且在第四象限,
∴﹣m>0,n<0,即m<0,n<0,
则一次函数y=mx+n不经过第一象限.
故答案为:一.
17.(2018秋?城厢区月考)如图所示四个二次函数的图象中,分别对应的是:①y=a1x2;②y=a2x2;③y=a3x2;则a1、a2、a3的大小关系是 a1>a2>a3 .
【分析】抛物线y=ax2的开口大小由|a|决定.|a|越大,抛物线的开口越窄;|a|越小,抛物线的开口越宽,据此即可得到结论.
【解析】如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,
③y=a3x2,开口向下,则a3<0,
故a1>a2>a3.
故答案为a1>a2>a3.
18.(2018秋?顺河区校级月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=﹣2x2的图象,则阴影部分的面积是 8 .
【分析】根据题意,观察图形可得图中的阴影部分的面积是图中正方形面积的一半,而正方形面积为16,由此可以求出阴影部分的面积.
【解析】∵函数y=2x2与y=﹣2x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为8.
三.解答题(共7小题)
19.(2020?拱墅区模拟)在同一直角坐标系中画出二次函数yx2+1与二次函数yx2﹣1的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
【分析】根据二次函数图象,可得二次函数的性质.
【解析】如图:
,
(1)yx2+1与yx2﹣1的相同点是:形状都是抛物线,对称轴都是y轴,
yx2+1与yx2﹣1的不同点是:yx2+1开口向上,顶点坐标是(0,1),yx2﹣1开口向下,顶点坐标是(0,﹣1);
(2)性质的相同点:开口程度相同,不同点:yx2+1 当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;
yx2﹣1当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.
20.(2019秋?南昌县期中)已知点(3,13)在函数y=ax2+b的图象上,当x=﹣2时,y=8.
(1)求a,b的值;
(2)如果点(6,m),(n,20)也在这个函数的图象上,求m与n的值.
【分析】(1)把点(3,13),x=﹣2时,y=8代入函数y=ax2+b可得关于a、b的方程组,再解方程组即可;
(2)根据(1)可得函数解析式,再把点(6,m),(n,20)代入函数解析式可得答案.
【解析】(1)∵点(3,13)在函数y=ax2+b的图象上,
∴13=9a+b,
∵当x=﹣2时,y=8,
∴8=4a+b,
,
解得:;
(2)∵a=1,b=4,
∴函数解析式为y=x2+4,
∵点(6,m),(n,20)也在这个函数的图象上,
∴m=36+4=40,20=n2+4,
∴n=±4,
则m=40,n=±4.
21.(2019秋?衢州期中)已知二次函数的表达式为y=﹣3(x﹣3)2+2.
(1)写出该函数的顶点坐标;
(2)判断点(1,﹣12)是否在这个函数的图象上.
【分析】(1)直接根据顶点式写出顶点坐标即可;
(2)将点代入函数的解析式后满足则在函数图象上,否则不在.
【解析】(1)∵二次函数的表达式为y=﹣3(x﹣3)2+2.
∴顶点(3,2);
(2)当x=1时,
y=﹣3×4+2=﹣10.
所以点(1,﹣12)不在函数图象上;
22.(2019秋?萧山区期中)已知二次函数y(x﹣1)2
(1)完成下表;
x … ﹣2 ﹣1 0 1 2 3 4 …
y … ﹣2 0 ﹣2 …
(2)在如图的坐标系中描点,画出该二次函数的图象.
【分析】(1)选取合适的x的值,求出对应的y的值即可完成表格,;
(2)利用描点法画出函数图象.
【解析】(1)完成表格如下:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … ﹣2 0 ﹣2 …
(2)描点,画出该二次函数图象如下:
23.(2019秋?丹江口市期中)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A,B两点,
(1)求A,B两点的坐标.
(2)求△ABO的面积.
【分析】(1)联立两函数解析式求解即可;
(2)利用三角形面积计算方法即可求得△ABO的面积.
【解析】(1)联立,
解得:或,
所以A、B两点的坐标分别是(﹣1,0),(0,2);
(2)∵A、B两点的坐标分别是(﹣1,0),(0,2),
∴OA=1,OB=2,
∴S△OABOA?OB1
24.(2019秋?思明区校级期中)已知二次函数y=x2+k的图象经过点(﹣2,3)
(1)求二次函数的解析式;
(2)画出此二次函数的图象.
【分析】(1)把已知点的坐标代入入y=x2+k中求出即可得到抛物线解析式;
(2)利用描点法画图.
【解析】(1)把(﹣2,3)代入y=x2+k得4+k=3,解得k=1,
所以二次函数的解析式为y=x2﹣1;
(2)抛物线y=x2﹣1的顶点坐标为(0,﹣1),
当y=0时,x2﹣1=0,解得x1=1,x2=﹣1,则抛物线与x轴的交点坐标为(﹣1,0),(1,0),
如图,
25.(2019秋?包河区期中)抛物线y=a(x+h)2的顶点为(2,0),它的形状与y=3x2相同,但开口方向与之相反.
(1)直接写出抛物线的解析式;
(2)求抛物线与y轴的交点坐标.
【分析】(1)由抛物线y=a(x+h)2的顶点为(2,0),得出h=﹣2,抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,得出a=﹣3,从而确定该抛物线的函数表达式;
(2)根据图象上点的坐标特征求得即可.
【解析】(1)∵抛物线y=a(x+h)2的顶点为(2,0),
∴﹣h=2,
∴h=﹣2,
抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反
∴a=﹣3,
则该抛物线的函数表达式是y=﹣3(x﹣2)2.
(2)在函数y=﹣3(x﹣2)2中,令x=0,则y=﹣12,
∴抛物线与y轴的交点坐标为(0,﹣12).
_21?????????è?????(www.21cnjy.com)_
专题1.2二次函数的图象(1)
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分100分,考试时间45分钟,试题共25题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)函数y=ax2﹣1与y=ax(a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
2.(2019秋?长春期末)二次函数y=(x+1)2﹣2的图象大致是( )
A. B.
C. D.
3.(2019秋?巴彦县期末)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
4.(2020?南宁一模)如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A. B.
C. D.
5.(2019秋?海曙区期末)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下
B.当x=﹣1时,y有最大值是2
C.对称轴是x=﹣1
D.顶点坐标是(1,2)
6.(2020?东莞市一模)如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
7.(2020?嘉兴)已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
8.(2020?宁波模拟)已知点P(m,n)在抛物线y=a(x﹣5)2+9(a≠0)上,当3<m<4时,总有n>1,当7<m<8时,总有n<1,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
9.(2020?永嘉县模拟)已知抛物线y=a(x﹣2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2,则m的取值范围是( )
A.0<m<1 B.0<m<2 C.1<m<2 D.m<2
10.(2020?雁塔区校级一模)已知抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,则下列说法正确的是( )
A.a>0
B.h<0
C.k≥3
D.当x<0时,y随x的增大而增大
二.填空题(共8小题)
11.(2020?哈尔滨)抛物线y=3(x﹣1)2+8的顶点坐标为 .
12.(2020?黄岩区模拟)二次函数y=x2﹣1图象的顶点坐标是 .
13.(2020?三门县一模)已知函数y,在自变量x≤m的范围内,相应的函数最小值为0,则m的取值范围是 .
14.(2020春?武邑县校级月考)若函数y,则当函数值y=12时,自变量x的值是 .
15.(2020?奉贤区一模)如果二次函数y=a(x﹣1)2(a≠0)的图象在它的对称轴右侧部分是上升的,那么a的取值范围是 .
16.(2019秋?溧阳市期末)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第 象限.
17.(2018秋?城厢区月考)如图所示四个二次函数的图象中,分别对应的是:①y=a1x2;②y=a2x2;③y=a3x2;则a1、a2、a3的大小关系是 .
18.(2018秋?顺河区校级月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=﹣2x2的图象,则阴影部分的面积是 .
三.解答题(共7小题)
19.(2020?拱墅区模拟)在同一直角坐标系中画出二次函数yx2+1与二次函数yx2﹣1的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
20.(2019秋?南昌县期中)已知点(3,13)在函数y=ax2+b的图象上,当x=﹣2时,y=8.
(1)求a,b的值;
(2)如果点(6,m),(n,20)也在这个函数的图象上,求m与n的值.
21.(2019秋?衢州期中)已知二次函数的表达式为y=﹣3(x﹣3)2+2.
(1)写出该函数的顶点坐标;
(2)判断点(1,﹣12)是否在这个函数的图象上.
22.(2019秋?萧山区期中)已知二次函数y(x﹣1)2
(1)完成下表;
x … …
y … …
(2)在如图的坐标系中描点,画出该二次函数的图象.
23.(2019秋?丹江口市期中)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A,B两点,
(1)求A,B两点的坐标.
(2)求△ABO的面积.
24.(2019秋?思明区校级期中)已知二次函数y=x2+k的图象经过点(﹣2,3)
(1)求二次函数的解析式;
(2)画出此二次函数的图象.
25.(2019秋?包河区期中)抛物线y=a(x+h)2的顶点为(2,0),它的形状与y=3x2相同,但开口方向与之相反.
(1)直接写出抛物线的解析式;
(2)求抛物线与y轴的交点坐
专题1.2二次函数的图象(1)解析版
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2019秋?莫旗期末)函数y=ax2﹣1与y=ax(a≠0)在同一直角坐标系中的图象可能是( )
A. B. C. D.
【分析】本题可先抛物线与y轴的交点排除C、D,然后根据一次函数y=ax图象得到a的正负,再与二次函数y=ax2的图象相比较看是否一致.
【解析】由函数y=ax2﹣1可知抛物线与y轴交于点(0,﹣1),故C、D错误;
A、由抛物线可知,a>0,由直线可知,a<0,故A错误;
B、由抛物线可知,a>0,由直线可知,a>0,故B正确;
故选:B.
2.(2019秋?长春期末)二次函数y=(x+1)2﹣2的图象大致是( )
A.B. C.D.
【分析】分别根据抛物线的开口方向、对称轴的位置及抛物线与y轴的交点位置逐一判断可得.
【解析】在y=(x+1)2﹣2中由a=1>0知抛物线的开口向上,故A错误;
其对称轴为直线x=﹣1,在y轴的左侧,故B错误;
由y=(x+1)2﹣2=x2+2x﹣1知抛物线与y轴的交点为(0,﹣1),在y轴的负半轴,故D错误;
故选:C.
3.(2019秋?巴彦县期末)如图,当ab>0时,函数y=ax2与函数y=bx+a的图象大致是( )
A. B.
C. D.
【分析】根据一次函数和二次函数的图象得出a、b的范围,看看是否相同且ab>0即可.
【解析】A、根据一次函数得出a<0,b>0,根据二次函数得出a>0,则ab<0,故本选项错误;
B、根据一次函数得出a>0,b<0,根据二次函数得出a>0,则ab<0,故本选项错误;
C、根据一次函数得出a<0,b<0,根据二次函数得出a<0,则ab>0,故本选项正确;
D、根据一次函数得出a<0,b>0,根据二次函数得出a<0,则ab<0,故本选项错误;
故选:C.
4.(2020?南宁一模)如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A. B.
C. D.
【分析】根据函数图象与y轴的交点,可得m>0,根据二次函数图象当x=a时,y<0,可得a>0,a﹣1<0,根据一次函数的性质,可得答案.
【解析】把x=a代入函数y=x2﹣x+m,得y=a2﹣a+m=a(a﹣1)+m,
∵x=a时,y<0,即 a(a﹣1)+m<0.
由图象交y轴的正半轴于点C,得m>0,
即a(a﹣1)<0.
x=a时,y<0,∴a>0,a﹣1<0,
∴一次函数y=(a﹣1)x+m的图象过一二四象限,
故选:A.
5.(2019秋?海曙区期末)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向下
B.当x=﹣1时,y有最大值是2
C.对称轴是x=﹣1
D.顶点坐标是(1,2)
【分析】根据二次函数的性质对各选项进行判断.
【解析】二次函数y=(x﹣1)2+2的图象的开口向上,故A错误;
当x=1时,函数有最小值2,故B错误;
对称轴为直线x=1,故C错误;
顶点坐标为(1,2),故D正确.
故选:D.
6.(2020?东莞市一模)如图在同一个坐标系中函数y=kx2和y=kx﹣2(k≠0)的图象可能的是( )
A. B.
C. D.
【分析】分两种情况进行讨论:k>0与k<0进行讨论即可.
【解析】当k>0时,函数y=kx﹣2的图象经过一、三、四象限;函数y=kx2的开口向上,对称轴在y轴上;
当k<0时,函数y=kx﹣2的图象经过二、三、四象限;函数y=kx2的开口向下,对称轴在y轴上,故C正确.
故选:C.
7.(2020?嘉兴)已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
【分析】方法1、①当b﹣a=1时,当a,b同号时,先判断出四边形BCDE是矩形,得出BC=DE=b﹣a=1,CD=BE=m,进而得出AC=n﹣m,即tan∠ABC=n﹣m,再判断出45°≤∠ABC<90°,即可得出n﹣m的范围,当a,b异号时,m=0,当a,b时,n最小,即可得出n﹣m的范围;
②当n﹣m=1时,当a,b同号时,同①的方法得出NH=PQ=b﹣a,HQ=PN=m,进而得出MH=n﹣m=1,而tan∠MHN,再判断出45°≤∠MNH<90°,当a,b异号时,m=0,则n=1,即可求出a,b,即可得出结论.
方法2、根据抛物线的性质判断,即可得出结论.
【解析】方法1、①当b﹣a=1时,当a,b同号时,如图1,
过点B作BC⊥AD于C,
∴∠BCD=90°,
∵∠ADE=∠BED=90°,
∴∠ADD=∠BCD=∠BED=90°,
∴四边形BCDE是矩形,
∴BC=DE=b﹣a=1,CD=BE=m,
∴AC=AD﹣CD=n﹣m,
在Rt△ACB中,tan∠ABCn﹣m,
∵点A,B在抛物线y=x2上,且a,b同号,
∴45°≤∠ABC<90°,
∴tan∠ABC≥1,
∴n﹣m≥1,
当a,b异号时,m=0,
当a,b时,n,此时,n﹣m,
∴n﹣m<1,
即n﹣m,
即n﹣m无最大值,有最小值,最小值为,故选项C,D都错误;
②当n﹣m=1时,如图2,
当a,b同号时,过点N作NH⊥MQ于H,
同①的方法得,NH=PQ=b﹣a,HQ=PN=m,
∴MH=MQ﹣HQ=n﹣m=1,
在Rt△MHN中,tan∠MNH,
∵点M,N在抛物线y=x2上,
∴m≥0,
当m=0时,n=1,
∴点N(0,0),M(1,1),
∴NH=1,
此时,∠MNH=45°,
∴45°≤∠MNH<90°,
∴tan∠MNH≥1,
∴1,
当a,b异号时,m=0,
∴n=1,
∴a=﹣1,b=1,
即b﹣a=2,
∴b﹣a无最小值,有最大值,最大值为2,故选项A错误;
故选:B.
方法2、当n﹣m=1时,
当a,b在y轴同侧时,a,b都越大时,a﹣b越接近于0,但不能取0,即b﹣a没有最小值,
当a,b异号时,当a=﹣1,b=1时,b﹣a=2最大,
当b﹣a=1时,当a,b在y轴同侧时,a,b离y轴越远,n﹣m越大,但取不到最大,
当a,b在y轴两侧时,当a,b时,n﹣m取到最小,最小值为,
因此,只有选项B正确,
故选:B.
8.(2020?宁波模拟)已知点P(m,n)在抛物线y=a(x﹣5)2+9(a≠0)上,当3<m<4时,总有n>1,当7<m<8时,总有n<1,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
【分析】依解析式可知顶点坐标,根据当7<m<8时,总有n<1,可知a<0,由增减性可列不等式组,解出即可.
【解析】∵抛物线y=a(x﹣5)2+9(a≠0),
∴抛物线的顶点为(5,9),
∵当7<m<8时,总有n<1,
∴a不可能大于0,
则a<0,
∴x<5时,y随x的增大而增大,x>5时,y随x的增大而减小,
∵当3<m<4时,总有n>1,当7<m<8时,总有n<1,且x=3与x=7对称,
∴m=3时,n≤1,m=7时,n≥1,
∴,
∴4a+9=1,
∴a=﹣2,
故选:D.
9.(2020?永嘉县模拟)已知抛物线y=a(x﹣2)2+1经过点A(m,y1),B(m+2,y2),若点A在抛物线对称轴的左侧,且1<y1<y2,则m的取值范围是( )
A.0<m<1 B.0<m<2 C.1<m<2 D.m<2
【分析】根据题目中的抛物线,可以得到该抛物线的对称轴,然后根据题意,可知点A和点B在对称轴两侧,从而可以得到m的取值范围,本题得以解决.
【解析】∵抛物线y=a(x﹣2)2+1,
∴该抛物线的对称轴为直线x=2,
∵点A(m,y1),B(m+2,y2)在抛物线y=a(x﹣2)2+1上,点A在抛物线对称轴的左侧,且1<y1<y2,
∴1<m<2,
故选:C.
10.(2020?雁塔区校级一模)已知抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,则下列说法正确的是( )
A.a>0
B.h<0
C.k≥3
D.当x<0时,y随x的增大而增大
【分析】利用对称性得到抛物线对称轴为直线x=1,根据点的坐标确定开口向下,最大值大于3,根据二次函数的性质即可判断D正确.
【解析】∵抛物线y=a(x﹣h)2+k(a≠0)经过A(m﹣4,0),B(m﹣2,3),C(4﹣m,3)三点,其中m<3,
∴抛物线的开口向下,对称轴为直线x1,即a<0,h=1,
∴k>3,当x<1时,y随x的增大而增大,
故选:D.
二.填空题(共8小题)
11.(2020?哈尔滨)抛物线y=3(x﹣1)2+8的顶点坐标为 (1,8) .
【分析】已知抛物线顶点式y=a(x﹣h)2+k,顶点坐标是(h,k).
【解析】∵抛物线y=3(x﹣1)2+8是顶点式,
∴顶点坐标是(1,8).
故答案为:(1,8).
12.(2020?黄岩区模拟)二次函数y=x2﹣1图象的顶点坐标是 (0,﹣1) .
【分析】根据二次函数的性质,利用顶点式直接得出顶点坐标即可.
【解析】二次函数y=x2﹣1图象的顶点坐标是:(0,﹣1).
故答案为:(0,﹣1).
13.(2020?三门县一模)已知函数y,在自变量x≤m的范围内,相应的函数最小值为0,则m的取值范围是 1≤m≤3 .
【分析】画出函数的图象,根据函数的图象即可求得.
【解析】画出函数y的图象如图:
在自变量x≤m的范围内,相应的函数最小值为0,由图象可知:m的取值范围是1≤m≤3,
故答案为1≤m≤3.
14.(2020春?武邑县校级月考)若函数y,则当函数值y=12时,自变量x的值是 6或 .
【分析】根据函数y,分两种两种情况,令y=12代入分别求得相应的x的值,本题得以解决.
【解析】∵函数y,
∴当x≤2时,令x2+2=12,得x,
当x>2时,令2x=12,得x=6,
故答案为:6或.
15.(2020?奉贤区一模)如果二次函数y=a(x﹣1)2(a≠0)的图象在它的对称轴右侧部分是上升的,那么a的取值范围是 a>0 .
【分析】由于二次函数的图象在对称轴x=2的右侧部分是上升的,由此可以确定二次函数的二次项系数为正数.
【解析】∵二次函数的图象在对称轴x=1的右侧部分是上升的,
∴这个二次函数的二次项系数为正数,
∴a>0,
故答案为a>0.
16.(2019秋?溧阳市期末)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第 一 象限.
【分析】由二次函数解析式表示出顶点坐标,根据图形得到顶点在第四象限,求出m与n的正负,即可作出判断.
【解析】根据题意得:抛物线的顶点坐标为(﹣m,n),且在第四象限,
∴﹣m>0,n<0,即m<0,n<0,
则一次函数y=mx+n不经过第一象限.
故答案为:一.
17.(2018秋?城厢区月考)如图所示四个二次函数的图象中,分别对应的是:①y=a1x2;②y=a2x2;③y=a3x2;则a1、a2、a3的大小关系是 a1>a2>a3 .
【分析】抛物线y=ax2的开口大小由|a|决定.|a|越大,抛物线的开口越窄;|a|越小,抛物线的开口越宽,据此即可得到结论.
【解析】如图所示:①y=a1x2的开口小于②y=a2x2的开口,则a1>a2>0,
③y=a3x2,开口向下,则a3<0,
故a1>a2>a3.
故答案为a1>a2>a3.
18.(2018秋?顺河区校级月考)如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y=2x2与y=﹣2x2的图象,则阴影部分的面积是 8 .
【分析】根据题意,观察图形可得图中的阴影部分的面积是图中正方形面积的一半,而正方形面积为16,由此可以求出阴影部分的面积.
【解析】∵函数y=2x2与y=﹣2x2的图象关于x轴对称,
∴图中的阴影部分的面积是图中正方形面积的一半,
而边长为4的正方形面积为16,
所以图中的阴影部分的面积是8.
故答案为8.
三.解答题(共7小题)
19.(2020?拱墅区模拟)在同一直角坐标系中画出二次函数yx2+1与二次函数yx2﹣1的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
【分析】根据二次函数图象,可得二次函数的性质.
【解析】如图:
,
(1)yx2+1与yx2﹣1的相同点是:形状都是抛物线,对称轴都是y轴,
yx2+1与yx2﹣1的不同点是:yx2+1开口向上,顶点坐标是(0,1),yx2﹣1开口向下,顶点坐标是(0,﹣1);
(2)性质的相同点:开口程度相同,不同点:yx2+1 当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;
yx2﹣1当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.
20.(2019秋?南昌县期中)已知点(3,13)在函数y=ax2+b的图象上,当x=﹣2时,y=8.
(1)求a,b的值;
(2)如果点(6,m),(n,20)也在这个函数的图象上,求m与n的值.
【分析】(1)把点(3,13),x=﹣2时,y=8代入函数y=ax2+b可得关于a、b的方程组,再解方程组即可;
(2)根据(1)可得函数解析式,再把点(6,m),(n,20)代入函数解析式可得答案.
【解析】(1)∵点(3,13)在函数y=ax2+b的图象上,
∴13=9a+b,
∵当x=﹣2时,y=8,
∴8=4a+b,
,
解得:;
(2)∵a=1,b=4,
∴函数解析式为y=x2+4,
∵点(6,m),(n,20)也在这个函数的图象上,
∴m=36+4=40,20=n2+4,
∴n=±4,
则m=40,n=±4.
21.(2019秋?衢州期中)已知二次函数的表达式为y=﹣3(x﹣3)2+2.
(1)写出该函数的顶点坐标;
(2)判断点(1,﹣12)是否在这个函数的图象上.
【分析】(1)直接根据顶点式写出顶点坐标即可;
(2)将点代入函数的解析式后满足则在函数图象上,否则不在.
【解析】(1)∵二次函数的表达式为y=﹣3(x﹣3)2+2.
∴顶点(3,2);
(2)当x=1时,
y=﹣3×4+2=﹣10.
所以点(1,﹣12)不在函数图象上;
22.(2019秋?萧山区期中)已知二次函数y(x﹣1)2
(1)完成下表;
x … ﹣2 ﹣1 0 1 2 3 4 …
y … ﹣2 0 ﹣2 …
(2)在如图的坐标系中描点,画出该二次函数的图象.
【分析】(1)选取合适的x的值,求出对应的y的值即可完成表格,;
(2)利用描点法画出函数图象.
【解析】(1)完成表格如下:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … ﹣2 0 ﹣2 …
(2)描点,画出该二次函数图象如下:
23.(2019秋?丹江口市期中)如图,已知抛物线y1=﹣2x2+2与直线y2=2x+2交于A,B两点,
(1)求A,B两点的坐标.
(2)求△ABO的面积.
【分析】(1)联立两函数解析式求解即可;
(2)利用三角形面积计算方法即可求得△ABO的面积.
【解析】(1)联立,
解得:或,
所以A、B两点的坐标分别是(﹣1,0),(0,2);
(2)∵A、B两点的坐标分别是(﹣1,0),(0,2),
∴OA=1,OB=2,
∴S△OABOA?OB1
24.(2019秋?思明区校级期中)已知二次函数y=x2+k的图象经过点(﹣2,3)
(1)求二次函数的解析式;
(2)画出此二次函数的图象.
【分析】(1)把已知点的坐标代入入y=x2+k中求出即可得到抛物线解析式;
(2)利用描点法画图.
【解析】(1)把(﹣2,3)代入y=x2+k得4+k=3,解得k=1,
所以二次函数的解析式为y=x2﹣1;
(2)抛物线y=x2﹣1的顶点坐标为(0,﹣1),
当y=0时,x2﹣1=0,解得x1=1,x2=﹣1,则抛物线与x轴的交点坐标为(﹣1,0),(1,0),
如图,
25.(2019秋?包河区期中)抛物线y=a(x+h)2的顶点为(2,0),它的形状与y=3x2相同,但开口方向与之相反.
(1)直接写出抛物线的解析式;
(2)求抛物线与y轴的交点坐标.
【分析】(1)由抛物线y=a(x+h)2的顶点为(2,0),得出h=﹣2,抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反,得出a=﹣3,从而确定该抛物线的函数表达式;
(2)根据图象上点的坐标特征求得即可.
【解析】(1)∵抛物线y=a(x+h)2的顶点为(2,0),
∴﹣h=2,
∴h=﹣2,
抛物线y=a(x+h)2的形状与y=3x2的相同,开口方向相反
∴a=﹣3,
则该抛物线的函数表达式是y=﹣3(x﹣2)2.
(2)在函数y=﹣3(x﹣2)2中,令x=0,则y=﹣12,
∴抛物线与y轴的交点坐标为(0,﹣12).
_21?????????è?????(www.21cnjy.com)_
同课章节目录
