浙教版 八年级数学上册特殊三角形知识点归纳及练习(Word版 无答案)
文档属性
| 名称 | 浙教版 八年级数学上册特殊三角形知识点归纳及练习(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-18 00:00:00 | ||
图片预览



文档简介
《特殊三角形》知识点归纳及练习
【概念梳理】
▲特殊三角形:等腰三角形、等边三角形、直角三角形。
一、等腰三角形
1.等腰三角形的性质:
①等腰三角形两腰_______;等腰三角形两底角______(即在同一个三角形中,等边对__________);
②等腰三角形三线合一,这三线是指________________、________________、________________,也就是说这三线为同一条线段;
③等腰三角形是________图形,它的对称轴有_________条。
2.等腰三角形的判定:
①有____边相等的三角形是等腰三角形;
②有_____相等的三角形是等腰三角形(即在同一个三角形中,等角对_____)。
二、等边三角形
1.等边三角形的性质:
①等边三角形各条边______,各内角_______,且都等于_____;
②等边三角形是______图形,它有____条对称轴。
2.等边三角形的判定:
①有____边相等的三角形是等边三角形;
②有三个角都是______的三角形是等边三角形;
③有两个角都是______的三角形是等边三角形;
④有一个角是______的______
三角形是等边三角形。
三、直角三角形
1.直角三角形的性质:
①直角三角形两锐角_______;
②直角三角形斜边上的中线等于_______;
③直角三角形两直角边的平方和等于________(即勾股定理)。
④30°角所对的直角边等于斜边的________
2.直角三角形的判定:
①有一个角是______的三角形是直角三角形;
②有两个角_______的三角形是直角三角形;
③两边的平方和等于_______的三角形是直角三角形。
四、常用方法(数学思维)
1.
分类讨论思想(特别是在语言模糊的等腰三角形中);
2.
方程思想:主要用在折叠之后产生直角三角形时,运用勾股定理列方程;还有就是在等腰三角形中求角度,求边长;
3.等面积法。
【例题精讲】
一、等腰三角形的性质及判定
例1:已知等腰三角形一腰上的中线把周长分为18cm和21cm两部分,则它的三边长为________________
例2:如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是(
)
A.20°
B.30°
C.35°
D.40°
例3:如图所示,在等腰△ABC中,AD是BC边上的中线,点E在AD上。求证:BE=CE。
例4:如图,点D和点E在BC上,AB=AC,AD=AE,求证:BD=CE
例5:已知:D、E为BC边上的点,AD=AE,BD=EC.求证:AB=AC.
例6:
如图,在△ABC和△DCB中,AC与BD相交于点O.AB=DC,AC=BD.
(1)求证:△ABC≌△DCB;
(2)△OBC的形状是________?等腰三角形
.(直接写出结论,不需证明)
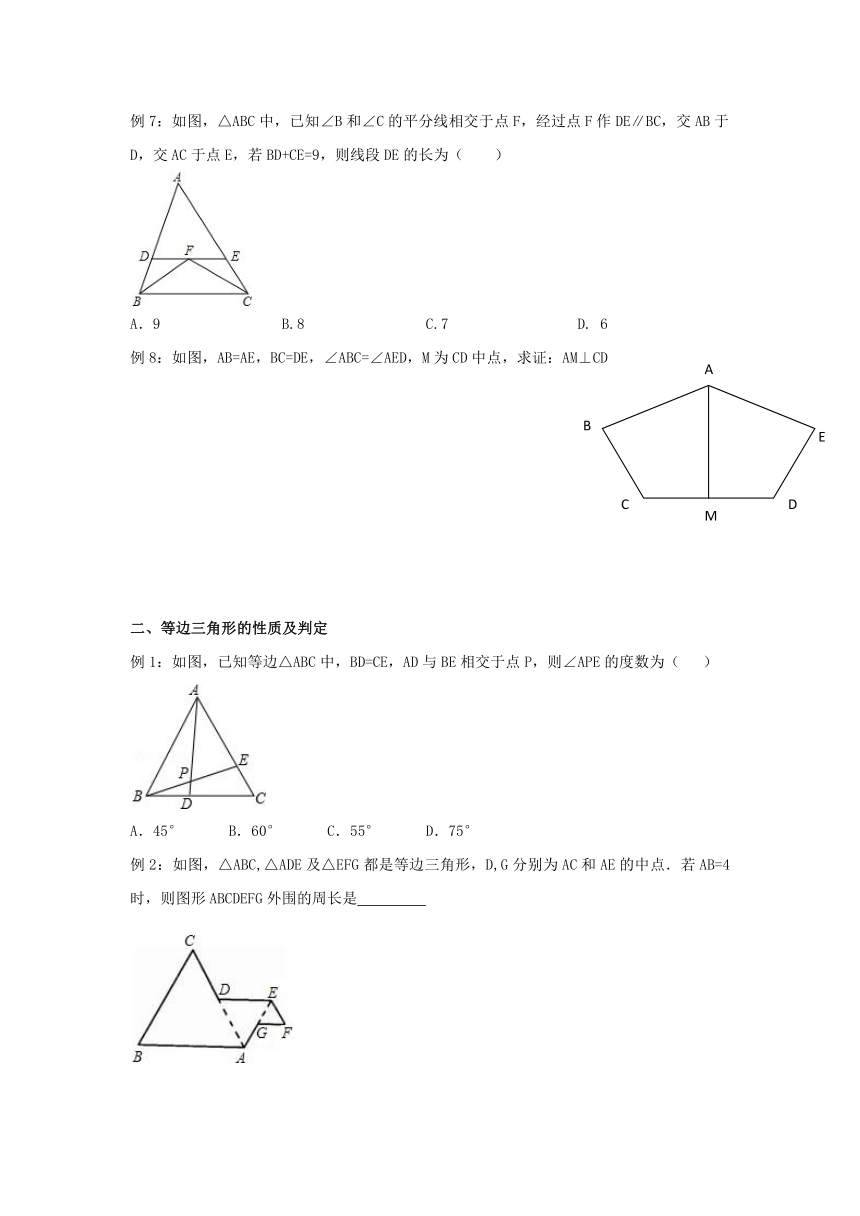
例7:如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE∥BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
A.9
B.8
C.7
D.
6
(
A
C
D
E
B
M
)例8:如图,AB=AE,BC=DE,∠ABC=∠AED,M为CD中点,求证:AM⊥CD
二、等边三角形的性质及判定
例1:如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数为(
)
A.45°
B.60°
C.55°
D.75°
例2:如图,△ABC,△ADE及△EFG都是等边三角形,D,G分别为AC和AE的中点.若AB=4时,则图形ABCDEFG外围的周长是
例3:一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A、C两地相距( )
:
A.30海里
B.40海里
C.50海里
D.60海里
例4:如图,在等边△ABC中,AF=BD=CE,则△DEF也是等边△,请说明理由.
三、直角三角形和勾股定理
例1:如果三角形的三个内角的比是1:2:3,那么这个三角形的是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角三角形或钝角三角
例2、如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连AE。
求证:(1)∠AEC=∠C;(2)BD=2AC。
例3:已知Rt△ABC中,∠ACB=90°,AB=8cm,D为AB中点,DE⊥AC于E,∠A=30°,求BC,CD和DE的长。
例4:轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25
B.25
C.50
D.25
例5:如果的三边长满足关系式,则
=________,=________,=________,的形状是______________.
例6:在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=.
(1)
求AD的长;
(2)
△ABC是直角三角形吗?请说明理由.
【巩固提高】
一、选择题
1.下列图形中,不一定是轴对称图形的是
(
)
A.线段
B.等腰三角形
C.直角三角形
D.圆
2.若等腰三角形的两边长分别为4和9,则周长为(
)
A.17
B.22
C.13
D.17或22
3.如果三角形一边上的高平分这条边所对的角,那么此三角形一定是(
)
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
4.小明将两个全等且有一个角为60°的直角三角板拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是(
)
A.4
B.3
C.2
D.1
5.如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D,E为垂足,下列结论正确的是(
)
A.AC=2AB
B.AC=8EC
C.CE=BD
D.BC=2BD
6.有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有(
)
A.1个
B.2个
C.3个
D.4个
7.如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,有以下判断:①DE=AC;②DE⊥AC;③∠CAB=30°;④∠EAF=∠ADE.其中正确结论的个数是(
)
A.1
B.2
C.3
D.4
8.如图,以点A和点B为两个顶点作位置不同的等腰直角三角形,一共可以作出(
)
A.2个
B.4个
C.6个
D.8个
9.如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2=MB2等于
(
)
A.9
B.35
C.45
D.无法计算
10.若△ABC是直角三角形,两条直角边分别为5和12,在三角形内有一
点D,D到△ABC各边的距离都相等,则这个距离等于
(
)
A.2
B.3
C.4
D.5
二、填空题
11.已知等腰三角形中顶角的度数是底角的3倍,那么底角的度数是________.
12.已知等腰△ABC的底边BC=8cm,且|AC-BC|=2cm,那么腰AC的长为__________.
13.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条小路,他们仅仅少走了_______步路,(假设2步为1m),却踩伤了花革.
14.如图,在△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为______cm.
15.已知,如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,不添加辅助线,请你写出三个正确结论:(1)____________;(2)_____________;(3)_____________.
16.已知,如图,正方形ABCD中,对角线AC和BD相交于点0,E,F分别是边AD,DC上的点,若AE=4cm,FC=3cm,且0E⊥0F,则EF=______cm.
三、解答题
17.如图,在△ABC中,AB=AC,点D在BC边上,DE⊥AB,DF⊥AC,垂足分别为E,F,添加一个条件,使DE=DF.
18.如图,已知∠AOB=30°,0C平分∠AOB,P为OC上一点,PD∥0A交OB于D,PE⊥OA于E,如果OD=4,求PE的长.
19.如图,△ABC是等边三角形,ABCD是等腰直角三角形,其中∠BCD=90°,求∠BAD的度数.
20.如图,E为等边三角形ABC边AC上的点,∠1=∠2,CD=BE,判断△ADE的形状.
21.如图所示,已知:在△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.
22.如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.(1)说明:△BCE≌△ACD;(2)说明:CF=CH;(3)判断△CFH的形状并说明理由.
【概念梳理】
▲特殊三角形:等腰三角形、等边三角形、直角三角形。
一、等腰三角形
1.等腰三角形的性质:
①等腰三角形两腰_______;等腰三角形两底角______(即在同一个三角形中,等边对__________);
②等腰三角形三线合一,这三线是指________________、________________、________________,也就是说这三线为同一条线段;
③等腰三角形是________图形,它的对称轴有_________条。
2.等腰三角形的判定:
①有____边相等的三角形是等腰三角形;
②有_____相等的三角形是等腰三角形(即在同一个三角形中,等角对_____)。
二、等边三角形
1.等边三角形的性质:
①等边三角形各条边______,各内角_______,且都等于_____;
②等边三角形是______图形,它有____条对称轴。
2.等边三角形的判定:
①有____边相等的三角形是等边三角形;
②有三个角都是______的三角形是等边三角形;
③有两个角都是______的三角形是等边三角形;
④有一个角是______的______
三角形是等边三角形。
三、直角三角形
1.直角三角形的性质:
①直角三角形两锐角_______;
②直角三角形斜边上的中线等于_______;
③直角三角形两直角边的平方和等于________(即勾股定理)。
④30°角所对的直角边等于斜边的________
2.直角三角形的判定:
①有一个角是______的三角形是直角三角形;
②有两个角_______的三角形是直角三角形;
③两边的平方和等于_______的三角形是直角三角形。
四、常用方法(数学思维)
1.
分类讨论思想(特别是在语言模糊的等腰三角形中);
2.
方程思想:主要用在折叠之后产生直角三角形时,运用勾股定理列方程;还有就是在等腰三角形中求角度,求边长;
3.等面积法。
【例题精讲】
一、等腰三角形的性质及判定
例1:已知等腰三角形一腰上的中线把周长分为18cm和21cm两部分,则它的三边长为________________
例2:如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是(
)
A.20°
B.30°
C.35°
D.40°
例3:如图所示,在等腰△ABC中,AD是BC边上的中线,点E在AD上。求证:BE=CE。
例4:如图,点D和点E在BC上,AB=AC,AD=AE,求证:BD=CE
例5:已知:D、E为BC边上的点,AD=AE,BD=EC.求证:AB=AC.
例6:
如图,在△ABC和△DCB中,AC与BD相交于点O.AB=DC,AC=BD.
(1)求证:△ABC≌△DCB;
(2)△OBC的形状是________?等腰三角形
.(直接写出结论,不需证明)
例7:如图,△ABC中,已知∠B和∠C的平分线相交于点F,经过点F作DE∥BC,交AB于D,交AC于点E,若BD+CE=9,则线段DE的长为( )
A.9
B.8
C.7
D.
6
(
A
C
D
E
B
M
)例8:如图,AB=AE,BC=DE,∠ABC=∠AED,M为CD中点,求证:AM⊥CD
二、等边三角形的性质及判定
例1:如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数为(
)
A.45°
B.60°
C.55°
D.75°
例2:如图,△ABC,△ADE及△EFG都是等边三角形,D,G分别为AC和AE的中点.若AB=4时,则图形ABCDEFG外围的周长是
例3:一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地,再由B地向北偏西20°的方向行驶40海里到达C地,则A、C两地相距( )
:
A.30海里
B.40海里
C.50海里
D.60海里
例4:如图,在等边△ABC中,AF=BD=CE,则△DEF也是等边△,请说明理由.
三、直角三角形和勾股定理
例1:如果三角形的三个内角的比是1:2:3,那么这个三角形的是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角三角形或钝角三角
例2、如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连AE。
求证:(1)∠AEC=∠C;(2)BD=2AC。
例3:已知Rt△ABC中,∠ACB=90°,AB=8cm,D为AB中点,DE⊥AC于E,∠A=30°,求BC,CD和DE的长。
例4:轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25
B.25
C.50
D.25
例5:如果的三边长满足关系式,则
=________,=________,=________,的形状是______________.
例6:在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=.
(1)
求AD的长;
(2)
△ABC是直角三角形吗?请说明理由.
【巩固提高】
一、选择题
1.下列图形中,不一定是轴对称图形的是
(
)
A.线段
B.等腰三角形
C.直角三角形
D.圆
2.若等腰三角形的两边长分别为4和9,则周长为(
)
A.17
B.22
C.13
D.17或22
3.如果三角形一边上的高平分这条边所对的角,那么此三角形一定是(
)
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
4.小明将两个全等且有一个角为60°的直角三角板拼成如图所示的图形,其中两条较长直角边在同一直线上,则图中等腰三角形的个数是(
)
A.4
B.3
C.2
D.1
5.如图,已知在△ABC中,∠ABC=90°,∠A=30°,BD⊥AC,DE⊥BC,D,E为垂足,下列结论正确的是(
)
A.AC=2AB
B.AC=8EC
C.CE=BD
D.BC=2BD
6.有四个三角形,分别满足下列条件:(1)一个角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为5,24,25.其中直角三角形有(
)
A.1个
B.2个
C.3个
D.4个
7.如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,有以下判断:①DE=AC;②DE⊥AC;③∠CAB=30°;④∠EAF=∠ADE.其中正确结论的个数是(
)
A.1
B.2
C.3
D.4
8.如图,以点A和点B为两个顶点作位置不同的等腰直角三角形,一共可以作出(
)
A.2个
B.4个
C.6个
D.8个
9.如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2=MB2等于
(
)
A.9
B.35
C.45
D.无法计算
10.若△ABC是直角三角形,两条直角边分别为5和12,在三角形内有一
点D,D到△ABC各边的距离都相等,则这个距离等于
(
)
A.2
B.3
C.4
D.5
二、填空题
11.已知等腰三角形中顶角的度数是底角的3倍,那么底角的度数是________.
12.已知等腰△ABC的底边BC=8cm,且|AC-BC|=2cm,那么腰AC的长为__________.
13.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条小路,他们仅仅少走了_______步路,(假设2步为1m),却踩伤了花革.
14.如图,在△ABC中,AB=5cm,BC=12cm,AC=13cm,那么AC边上的中线BD的长为______cm.
15.已知,如图,△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD,不添加辅助线,请你写出三个正确结论:(1)____________;(2)_____________;(3)_____________.
16.已知,如图,正方形ABCD中,对角线AC和BD相交于点0,E,F分别是边AD,DC上的点,若AE=4cm,FC=3cm,且0E⊥0F,则EF=______cm.
三、解答题
17.如图,在△ABC中,AB=AC,点D在BC边上,DE⊥AB,DF⊥AC,垂足分别为E,F,添加一个条件,使DE=DF.
18.如图,已知∠AOB=30°,0C平分∠AOB,P为OC上一点,PD∥0A交OB于D,PE⊥OA于E,如果OD=4,求PE的长.
19.如图,△ABC是等边三角形,ABCD是等腰直角三角形,其中∠BCD=90°,求∠BAD的度数.
20.如图,E为等边三角形ABC边AC上的点,∠1=∠2,CD=BE,判断△ADE的形状.
21.如图所示,已知:在△ABC中,∠A=80°,BD=BE,CD=CF.求∠EDF的度数.
22.如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.(1)说明:△BCE≌△ACD;(2)说明:CF=CH;(3)判断△CFH的形状并说明理由.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
