浙教版数学八年级上册课件:1.5全等三角形的判定②(23张)
文档属性
| 名称 | 浙教版数学八年级上册课件:1.5全等三角形的判定②(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
数学题是做出来的,
不是看出来的,
不是背出来的,
第一章
三角形初步知识
1.5
全等三角形判定②
A
B
C
E
F
G
ABC
≌
EFG
AB=EF
BC=FG
AC=EG
(SSS)
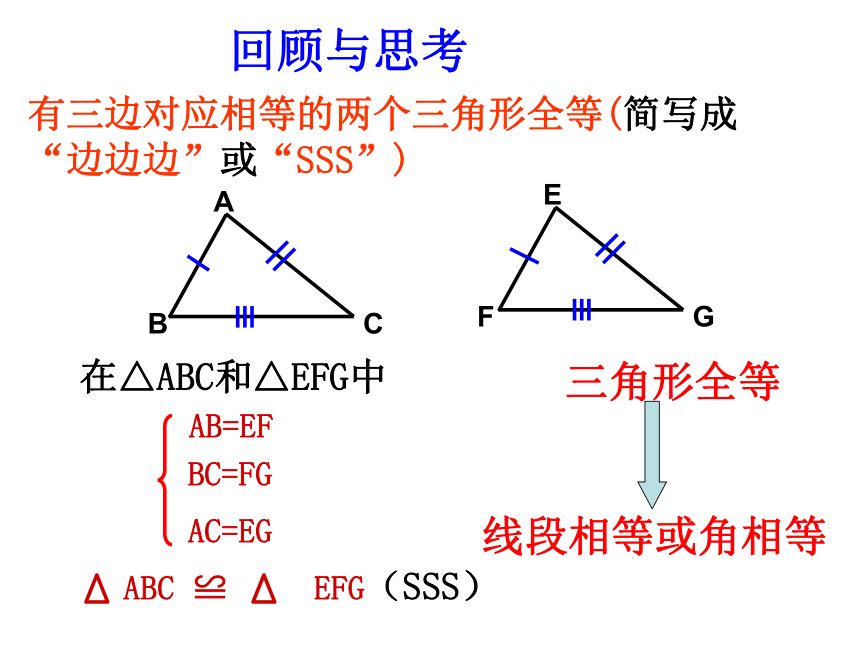
有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
在△ABC和△EFG中
回顾与思考
三角形全等
线段相等或角相等
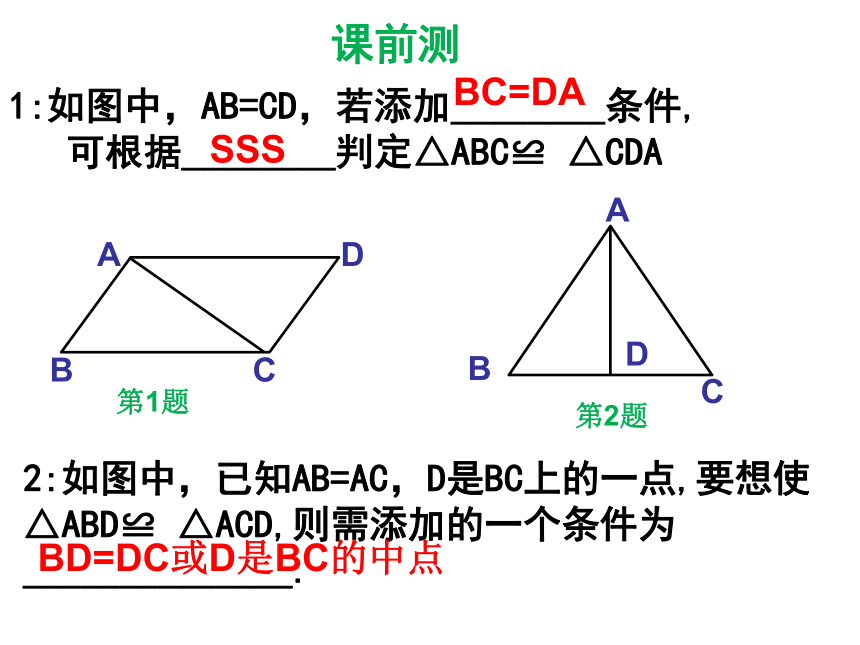
1:如图中,AB=CD,若添加________条件,
可根据________判定△ABC≌
△CDA
A
B
C
D
BC=DA
SSS
2:如图中,已知AB=AC,D是BC上的一点,要想使△ABD≌
△ACD,则需添加的一个条件为
______________.
A
B
C
D
BD=DC或D是BC的中点
课前测
第1题
第2题
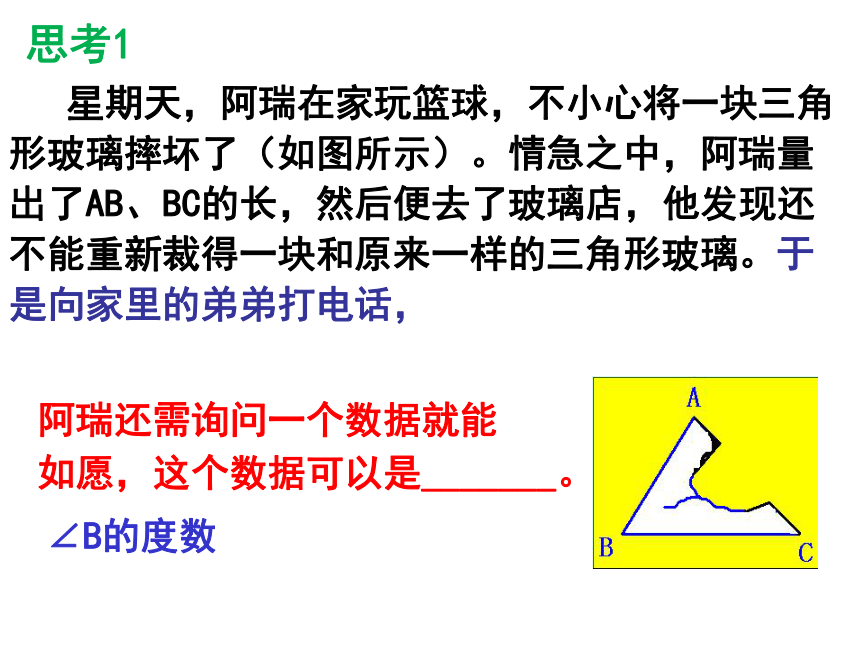
星期天,阿瑞在家玩篮球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,阿瑞量出了AB、BC的长,然后便去了玻璃店,他发现还不能重新裁得一块和原来一样的三角形玻璃。于是向家里的弟弟打电话,
阿瑞还需询问一个数据就能
如愿,这个数据可以是_______。
∠B的度数
思考1
4
6
4
6
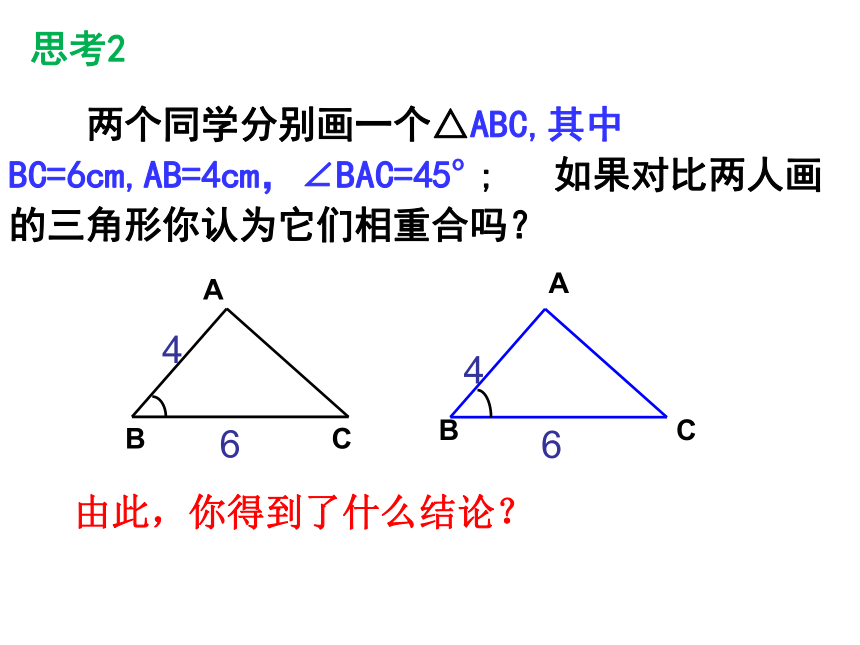
由此,你得到了什么结论?
A
B
C
A
C
B
两个同学分别画一个△ABC,其中BC=6cm,AB=4cm,∠BAC=45o
;
如果对比两人画的三角形你认为它们相重合吗?
思考2
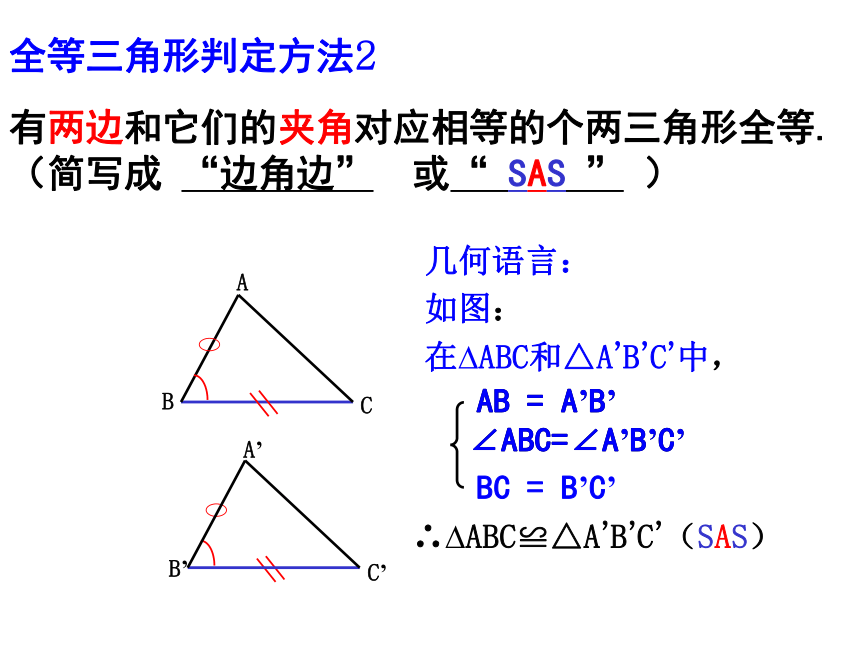
有两边和它们的夹角对应相等的个两三角形全等.
(简写成
“边角边”
或“
SAS
”
)
A
B
C
全等三角形判定方法2
几何语言:
如图:
在?ABC和△A’B’C’中,
AB
=
A’B’
∠ABC=∠A’B’C’
BC
=
B’C’
A’
B’
C’
∴?ABC≌△A’B’C’(SAS)
AB
=
A’B’
∠ABC=∠A’B’C’
S
S
SAS中
对于这个角有什么要求
注意:这个角一定要是这两边所夹的角
A
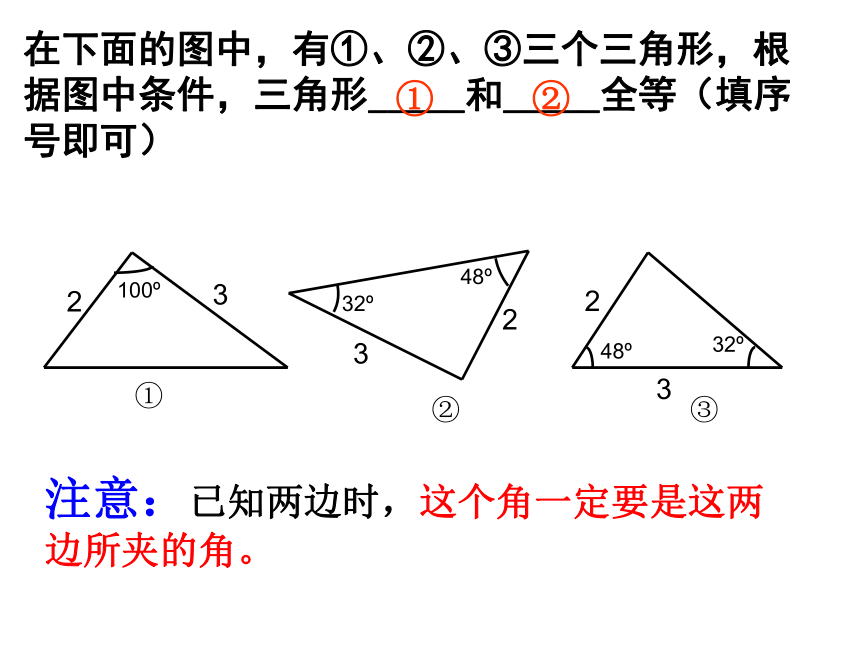
在下面的图中,有①、②、③三个三角形,根据图中条件,三角形_____和_____全等(填序号即可)
①
2
3
100?
③
2
3
48?
32?
②
2
3
48?
32?
①
②
注意:已知两边时,这个角一定要是这两边所夹的角。
例1:如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明AB//CD.
B
A
D
O
C
已知
对顶角相等
已知
证明:在?AOB和?COD中
OA
=
OC,(
)
∠A0B=∠COD,(
)
OB
=
OD,(
)
∴?AOB
≌
?COD(
)
SAS
温馨提示:在做几何问题时,将已知条件标在图形上是一个很好的办法,便于分析.
归纳:通过三角形全能可以得到线段或角相等。
例题讲解
∴
∠B=
∠D(
?
)
∴AB//CD(
)
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。
A
B
Aˊ
Bˊ
O
1、做一做(3分钟)
P29做一做
2、P30作业题2:
3、如图,已知ADC垂直于线段BC于E,且BE=EC,说出AB=AC的理由
A
E
D
B
C
2
1
E
D
B
A
C
A
B
A′
B′
O
归纳
1.若已知条件不足,可从图形中挖掘隐含条件,如公共边、公共角、对顶角等。
2.规范书写说理过程,最好按边角边的顺序书写。
3.“SAS”中的角必须是对应相等的两边的夹角。
如图,直线l垂直于线段AB于点O,且OA=OB.
O
B
A
l
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
性质:
线段垂直平分线上的点到线段两端点的距离相等
C
点C是线段垂直平分线上任意一点,连接AC、BC。线段AC、BC有什么关系?请说明理由.
线段的垂直平分线
如图,直线l是线段AB的垂直平分线.
C
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
解:已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB(
SAS)
∴CA=CB(全等三角形对应边相等)
∵直线
⊥AB
分类讨论的思想
垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。
垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。
式子表达为:
∴CA=CB
A
C
O
B
∵
是线段AB的中垂线,点C在
上
1、如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,且相交于点O.
点O到点A,B,C的距离相等吗?为什么?
l
m
∴OA=OB
OA=OC
(线段垂直平分线上的点到线段两端点的距离相等)
∵直线l和直线m分别是线段AB和线段AC的垂直平分线(已知)
解:连结OA,OB,OC
∴OA=OB=OC
例2:在△ABC中,AB=AC,D是AB的中点,DE⊥AB垂足为D,则△BCE的周长是8,且AC-BC=2,求AB,BC的长.
A
∟
D
C
B
E
①.如图(1),△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
如图,△ABC中,DE垂直平分AC,AE=2.5cm,
△ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
10cm
4cm
课堂小结
2.
线段垂直平分线的概念
三角形全等的判定方法
①全等三角形的定义
②边边边(sss)
③边角边或SAS)
3.
线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.
A
E
D
C
B
一级挑战:已知:如图,点E在AB上,AC=AD,
∠CAB=∠DAB,说明△BCE
≌
△BDE的理由.
适当拓展
二级挑战:在△ABC中,AB=BC=AC,
∠ABC=∠C=60°,EC=BD,AD与BE相交
于点P,求∠APE的度数.
A
E
P
D
C
B
三级挑战:在△ABC中,AB=5,AC=3,则BC上的中线AD的取值范围.
A
B
C
D
数学题是做出来的,
不是看出来的,
不是背出来的,
第一章
三角形初步知识
1.5
全等三角形判定②
A
B
C
E
F
G
ABC
≌
EFG
AB=EF
BC=FG
AC=EG
(SSS)
有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
在△ABC和△EFG中
回顾与思考
三角形全等
线段相等或角相等
1:如图中,AB=CD,若添加________条件,
可根据________判定△ABC≌
△CDA
A
B
C
D
BC=DA
SSS
2:如图中,已知AB=AC,D是BC上的一点,要想使△ABD≌
△ACD,则需添加的一个条件为
______________.
A
B
C
D
BD=DC或D是BC的中点
课前测
第1题
第2题
星期天,阿瑞在家玩篮球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,阿瑞量出了AB、BC的长,然后便去了玻璃店,他发现还不能重新裁得一块和原来一样的三角形玻璃。于是向家里的弟弟打电话,
阿瑞还需询问一个数据就能
如愿,这个数据可以是_______。
∠B的度数
思考1
4
6
4
6
由此,你得到了什么结论?
A
B
C
A
C
B
两个同学分别画一个△ABC,其中BC=6cm,AB=4cm,∠BAC=45o
;
如果对比两人画的三角形你认为它们相重合吗?
思考2
有两边和它们的夹角对应相等的个两三角形全等.
(简写成
“边角边”
或“
SAS
”
)
A
B
C
全等三角形判定方法2
几何语言:
如图:
在?ABC和△A’B’C’中,
AB
=
A’B’
∠ABC=∠A’B’C’
BC
=
B’C’
A’
B’
C’
∴?ABC≌△A’B’C’(SAS)
AB
=
A’B’
∠ABC=∠A’B’C’
S
S
SAS中
对于这个角有什么要求
注意:这个角一定要是这两边所夹的角
A
在下面的图中,有①、②、③三个三角形,根据图中条件,三角形_____和_____全等(填序号即可)
①
2
3
100?
③
2
3
48?
32?
②
2
3
48?
32?
①
②
注意:已知两边时,这个角一定要是这两边所夹的角。
例1:如图,AC与BD相交于点O,已知OA=OC,OB=OD,说明AB//CD.
B
A
D
O
C
已知
对顶角相等
已知
证明:在?AOB和?COD中
OA
=
OC,(
)
∠A0B=∠COD,(
)
OB
=
OD,(
)
∴?AOB
≌
?COD(
)
SAS
温馨提示:在做几何问题时,将已知条件标在图形上是一个很好的办法,便于分析.
归纳:通过三角形全能可以得到线段或角相等。
例题讲解
∴
∠B=
∠D(
?
)
∴AB//CD(
)
如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。
A
B
Aˊ
Bˊ
O
1、做一做(3分钟)
P29做一做
2、P30作业题2:
3、如图,已知ADC垂直于线段BC于E,且BE=EC,说出AB=AC的理由
A
E
D
B
C
2
1
E
D
B
A
C
A
B
A′
B′
O
归纳
1.若已知条件不足,可从图形中挖掘隐含条件,如公共边、公共角、对顶角等。
2.规范书写说理过程,最好按边角边的顺序书写。
3.“SAS”中的角必须是对应相等的两边的夹角。
如图,直线l垂直于线段AB于点O,且OA=OB.
O
B
A
l
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
性质:
线段垂直平分线上的点到线段两端点的距离相等
C
点C是线段垂直平分线上任意一点,连接AC、BC。线段AC、BC有什么关系?请说明理由.
线段的垂直平分线
如图,直线l是线段AB的垂直平分线.
C
OA=OB
∠COA=∠COB
OC=OC
B
A
C
O
解:已知OA=OB,当点C与点O重合时,显然CA=CB,
当点C与点O不重合时,
∴∠COA=∠BOC=90°
在△COA与△COB中
∴△COA≌△COB(
SAS)
∴CA=CB(全等三角形对应边相等)
∵直线
⊥AB
分类讨论的思想
垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。
垂直平分线的性质:线段的垂直平分线上的点到线段两端点的距离相等。
式子表达为:
∴CA=CB
A
C
O
B
∵
是线段AB的中垂线,点C在
上
1、如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,且相交于点O.
点O到点A,B,C的距离相等吗?为什么?
l
m
∴OA=OB
OA=OC
(线段垂直平分线上的点到线段两端点的距离相等)
∵直线l和直线m分别是线段AB和线段AC的垂直平分线(已知)
解:连结OA,OB,OC
∴OA=OB=OC
例2:在△ABC中,AB=AC,D是AB的中点,DE⊥AB垂足为D,则△BCE的周长是8,且AC-BC=2,求AB,BC的长.
A
∟
D
C
B
E
①.如图(1),△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.
A
B
C
D
E
如图,△ABC中,DE垂直平分AC,AE=2.5cm,
△ABC的周长是9cm,则△ABD的周长是_______.
A
B
C
D
E
10cm
4cm
课堂小结
2.
线段垂直平分线的概念
三角形全等的判定方法
①全等三角形的定义
②边边边(sss)
③边角边或SAS)
3.
线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.
A
E
D
C
B
一级挑战:已知:如图,点E在AB上,AC=AD,
∠CAB=∠DAB,说明△BCE
≌
△BDE的理由.
适当拓展
二级挑战:在△ABC中,AB=BC=AC,
∠ABC=∠C=60°,EC=BD,AD与BE相交
于点P,求∠APE的度数.
A
E
P
D
C
B
三级挑战:在△ABC中,AB=5,AC=3,则BC上的中线AD的取值范围.
A
B
C
D
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
