第四章 图形与坐标培优习题精选（含解析）

中小学教育资源及组卷应用平台
第四章 图形与坐标培优专题
一．选择题（共20小题）
1．（2020春?毕节市月考）已知点A的坐标为（1，3），点A向左平移1个单位长度，向下平移4个单位长度．则点A的对应点的坐标为（　　）
A．（5，3） B．（﹣1，﹣2） C．（﹣1，﹣1） D．（0，﹣1）
2．（2020?中原区校级模拟）在平面直角坐标系中，若干个半径为1个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为1个单位长度/秒，点在弧线上的速度为个单位长度/秒，则2021秒时，点P的坐标是（　　）
A．（2021，） B．
C． D．（2021，0）
3．（2020春?汉阳区校级期中）在平面直角坐标系xOy中，对于点P（x，y），我们把P1（y﹣1，﹣x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，这样依次得到各点．若A2020的坐标为（﹣3，2），设A1（x，y），则x+y的值是（　　）
A．﹣5 B．﹣1 C．3 D．5
4．（2020春?昌图县期末）若将点A（m+2，3）先向下平移1个单位，再向左平移2个单位，得到点B（2，n﹣1）则（　　）
A．m＝2，n＝3 B．m＝2，n＝5 C．m＝﹣6，n＝3 D．m＝﹣6，n＝5
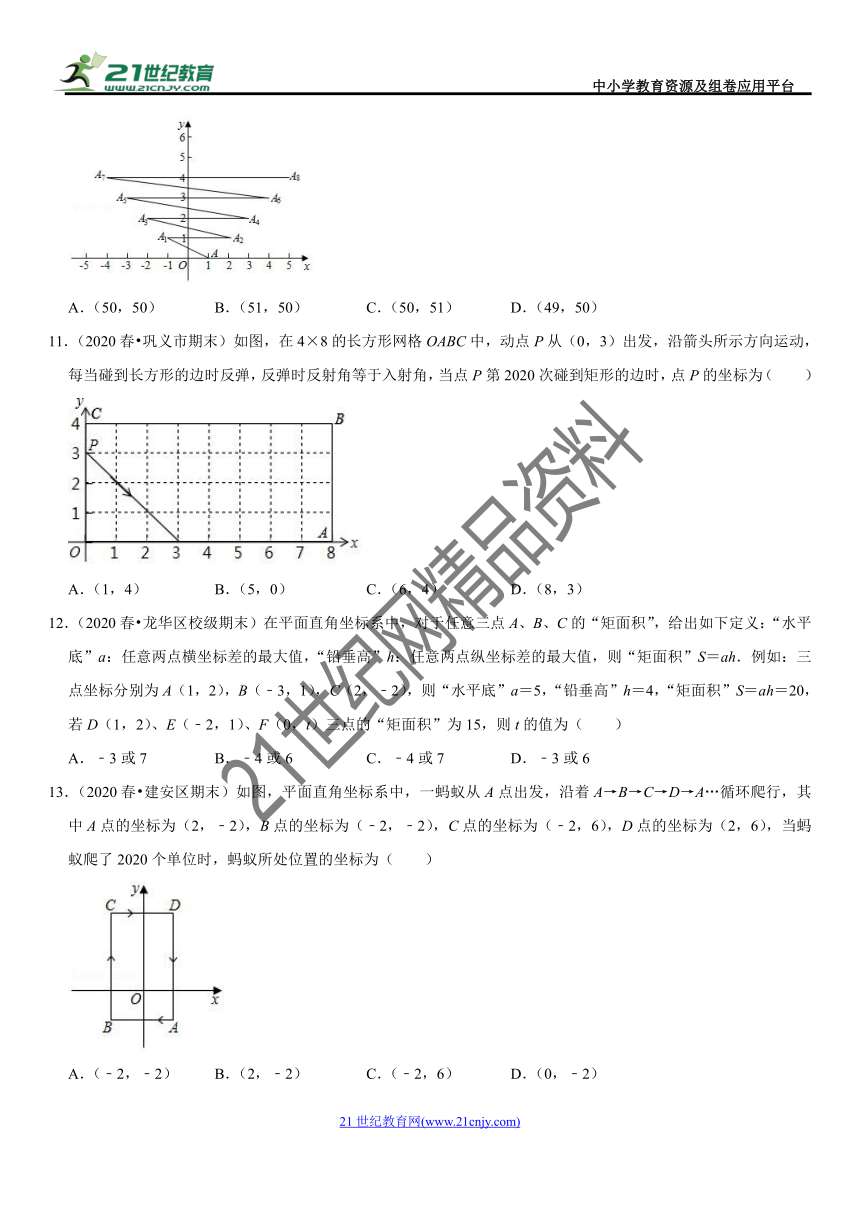
5．（2020春?濮阳期末）如图，已知点A1（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1），…，则点A2020的坐标为（　　）
A．（505，505） B．（506，﹣505） C．（﹣505，﹣505） D．（﹣505，505）
6．（2020春?岳阳期末）如图，已知正方形ABCD的对角线AC，BD相交于点M，顶点A、B、C的坐标分别为（1，3）、（1，1）、（3，1），规定“把正方形ABCD先沿x轴翻折，再向右平移1个单位”为一次变换，如此这样，连续经过2020次变换后，点M的坐标变为（　　）
A．（2022，2） B．（2022，﹣2） C．（2020，2） D．（2020，﹣2）
7．（2020春?罗山县期末）在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An，…．若点A1的坐标为（2，4），点A2020的坐标为（　　）
A．（﹣3，3） B．（﹣2，﹣2） C．（3，﹣1） D．（2，4）
8．（2020春?禹州市期末）在平面直角坐标系中，对于点P（x，y），我们把点P'（1﹣y，x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，…，这样依次得到点A1、A2、A3、A4…，若点A1的坐标为（3，2），则点A2020的坐标为（　　）
A．（3，2） B．（﹣1，2） C．（﹣1，﹣2） D．（3，﹣2）
9．（2020春?潼南区期末）如图，在平面直角坐标系中，OA1＝1，将边长为1的正方形一边与x轴重合按图中规律摆放，其中相邻两个正方形的间距都是1，则点A2022的坐标为（　　）
A．（1009，1） B．（1010，1） C．（1011，0） D．（1011，﹣1）
10．（2020春?莒县期末）如图，在平面直角坐标系上有点A（1，0），点A第一次跳至点A1（﹣1，1），第二次向右跳动3个单位至点A2（2，1），第三次跳至点A3（﹣2，2），第四次向右跳动5个单位至点A4（3，2），…依此规律跳动下去，点A第100次跳至点A100的坐标是（　　）
A．（50，50） B．（51，50） C．（50，51） D．（49，50）
11．（2020春?巩义市期末）如图，在4×8的长方形网格OABC中，动点P从（0，3）出发，沿箭头所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2020次碰到矩形的边时，点P的坐标为（　　）
A．（1，4） B．（5，0） C．（6，4） D．（8，3）
12．（2020春?龙华区校级期末）在平面直角坐标系中，对于任意三点A、B、C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S＝ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a＝5，“铅垂高”h＝4，“矩面积”S＝ah＝20，若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为15，则t的值为（　　）
A．﹣3或7 B．﹣4或6 C．﹣4或7 D．﹣3或6
13．（2020春?建安区期末）如图，平面直角坐标系中，一蚂蚁从A点出发，沿着A→B→C→D→A…循环爬行，其中A点的坐标为（2，﹣2），B点的坐标为（﹣2，﹣2），C点的坐标为（﹣2，6），D点的坐标为（2，6），当蚂蚁爬了2020个单位时，蚂蚁所处位置的坐标为（　　）
A．（﹣2，﹣2） B．（2，﹣2） C．（﹣2，6） D．（0，﹣2）
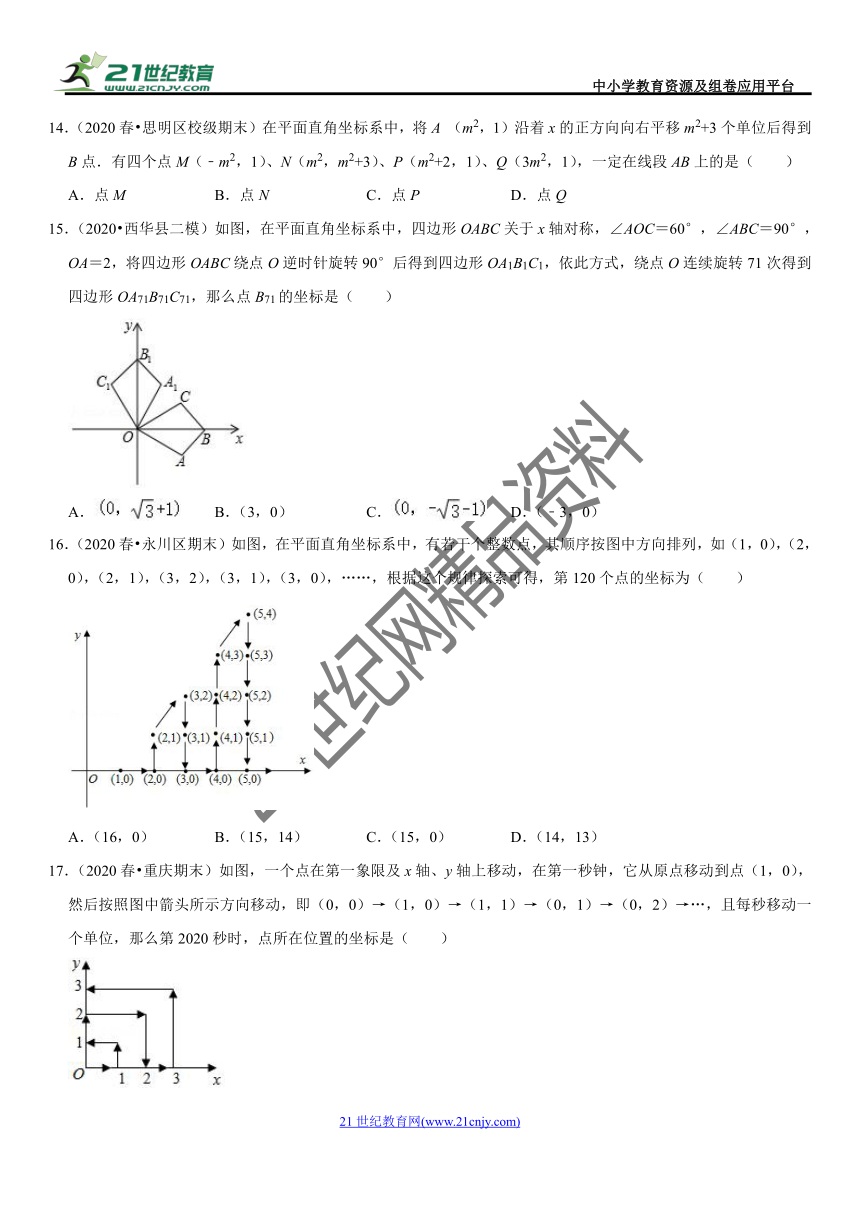
14．（2020春?思明区校级期末）在平面直角坐标系中，将A （m2，1）沿着x的正方向向右平移m2+3个单位后得到B点．有四个点M（﹣m2，1）、N（m2，m2+3）、P（m2+2，1）、Q（3m2，1），一定在线段AB上的是（　　）
A．点M B．点N C．点P D．点Q
15．（2020?西华县二模）如图，在平面直角坐标系中，四边形OABC关于x轴对称，∠AOC＝60°，∠ABC＝90°，OA＝2，将四边形OABC绕点O逆时针旋转90°后得到四边形OA1B1C1，依此方式，绕点O连续旋转71次得到四边形OA71B71C71，那么点B71的坐标是（　　）
A． B．（3，0） C． D．（﹣3，0）
16．（2020春?永川区期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），……，根据这个规律探索可得，第120个点的坐标为（　　）
A．（16，0） B．（15，14） C．（15，0） D．（14，13）
17．（2020春?重庆期末）如图，一个点在第一象限及x轴、y轴上移动，在第一秒钟，它从原点移动到点（1，0），然后按照图中箭头所示方向移动，即（0，0）→（1，0）→（1，1）→（0，1）→（0，2）→…，且每秒移动一个单位，那么第2020秒时，点所在位置的坐标是（　　）
A．（64，44） B．（45，5） C．（44，5） D．（44，4）
18．（2020春?南召县期末）如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA，OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2020的坐标为（　　）
A．（﹣21010，21010） B．（22020，﹣22020）
C．（﹣22020，﹣22020） D．（﹣21010，﹣21010）
19．（2020春?武鸣区校级期中）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），那么A2020坐标为（　　）
A．（2020，1） B．（2020，0） C．（1010，1） D．（1010，0）
20．（2020?河南一模）已知点E（x0，yo），点F（x2，y2），点M（x1，y1）是线段EF的中点，则x1＝，y1＝．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P1（即P，A，P1三点共线，且PA＝P1A），P1关于点B的对称点P2，P2关于点C的对称点P3，…按此规律继续以A，B，C三点为对称点重复前面的操作．依次得到点P4，P5，P6…，则点P2020的坐标是（　　）
A．（4，0） B．（﹣2，﹣2） C．（2，﹣4） D．（﹣4，2）
二．填空题（共10小题）
21．（2020春?崇川区校级期中）在平面直角坐标系中，将点P（2，﹣3）先向上平移1个单位长度，再向左平移3个单位长度后，得到点P′，则点P′的坐标为　 　．
22．（2020春?谢家集区期末）如图，在平面直角坐标系中，线段AB在x轴上，将线段AB向上平移2个单位．再向右平移1个单位，得到线段CD，连接AC，BD，在y轴上存在点P，使△PCD的面积为四边形ABDC面积的一半，则点P的坐标为　 　．
23．（2020春?市中区校级期中）在平面直角坐标系中，△OAB的位置如图所示，将△OAB绕点O顺时针旋转90°得△OA1B1；再将△OA1B1绕点O顺时针旋转90°得△OA2B2；再将△OA2B2绕点O顺时针旋转90°得△OA3B3；……依此类推，第2020次旋转得到△OA2020B2020，则项点A的对应点A2020的坐标是　 　．
24．在平面直角坐标系中，对于点P（a，b），我们把Q（﹣b+1，a+1）叫做点P的伴随点，已知A1的伴随点为A2，A2的伴随点为A3，…，这样依次下去得到A1，A2，A3，…，An，若A1的坐标为（3，1），则A2020的坐标为　 　．
25．（2020春?郯城县期末）如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2021秒时，点P的坐标是　 　．
26．（2020春?抚顺县期末）如图，在平面直角坐标系中，一动点从原点O出发，按向上﹣向右﹣向下﹣向右的方向依次平移，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A2020的坐标为　 　．
27．（2020春?禹城市期末）如图，在平面直角坐标系中，将△ABC绕点A顺时针旋转到△A1B1C1的位置，点B，O（分别落在点B1，C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去，…，若点A（，0），B（0，2），则点B2020的坐标为　 　．
28．（2020?新昌县模拟）在平面直角坐标系中，如果一个图形向右平移1个单位，再向上平移3个单位，称为一个变换，已知点A（1，﹣2），经过一个变换后对应点为A1，经过2个变换后对应点为A2，…经过n个变换后对应点为An，则用含n的代数式表示点An的坐标为　 　．
29．（2020春?博兴县期末）如图，动点P在平面直角坐标系中按箭头所示方向做折线运动，即第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1），…．按这样的运动规律，经过第2020次运动后，动点P的坐标是　 　．
30．（2020春?江汉区期末）如图，在平面直角坐标系中，有若干个横坐标和纵坐标分别为整数的点，其顺序按图中“→”方向排列，第1个点为（1，0），后面依次为（2，0），（1，2），（1，3），（2，2），（3，0）…，根据这个规律，第110个点的坐标为　 　．
三．解答题（共9小题）
31．（2020春?开福区校级期中）如图，△ABC向左平移3个单位，再向上平移1个单位得到△A1B1C1．已知A（2，1），B（5，3），C（3，4）．
（1）直接写出△A1B1C1三个顶点的坐标；
（2）求△ABC的面积．
32．（2020春?西乡塘区校级月考）已知点A（a﹣1，﹣2），B（﹣3，b+1），根据以下要求确定a，b的值．
（1）当直线AB∥x轴时，a　 　，b　 　；
（2）当直线AB∥y轴时，a　 　，b　 　；
（3）当点A和点B在二四象限的角平分线上时，求a，b的值．
33．（2020秋?滨州月考）如图，在平面直角坐标系中，图中的网格是由边长相等的小正方组成，点A、B、C的坐标分别为（﹣5，4），（﹣4，0）．（﹣5，﹣3）．
（1）请写出点D、E、F、G的坐标；
（2）求图中阴影部分（多边形ABCDEFG）的面积．
34．（2020春?渝水区校级月考）如图，在平面直角坐标系中，点A、B在坐标轴上，其中A（0，a）、B（b，0）满足：
（1）求A、B两点的坐标；
（2）将线段AB平移到CD，点A的对应点为C（﹣2，t），若三角形ABC的面积为8，求点D的坐标．
35．（2020秋?雨花区校级月考）在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“近似距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1（x1，y1）与点P2（x2，y2）的“近似距离”为|x1﹣x2|；若|x1﹣x2|＜|y1﹣y2|，则P1（x1，y1）与点P2（x2，y2）的“近似距离”为|y1﹣y2|；
（1）已知点P（﹣3，4）、点Q（1，1），则点P与点Q的“近似距离”为　 　．
（2）已知点A（0，﹣2），B为x轴上的动点，
①若点A与B的“近似距离为3”，写出满足条件的B点的坐标　 　．
②直接写出点A与点B的“近似距离”的最小值　 　．
（3）已知C（2m+2，m），D（1，0），写出点C与点D的“近似距离”的最小值及相应的C点坐标．
36．（2020春?海淀区校级期末）在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
若b′＝，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，2），点（﹣2，﹣5）的限变点的坐标是（﹣2，5），点（1，3）的限变点的坐标是（1，3）．
（1）①点（，﹣1）的限变点的坐标是　 　；
②如图1，在点A（﹣2，1）、B（2，1）中有一个点是直线y＝2上某一个点的限变点，这个点是　 　；（填“A”或“B”）
（2）如图2，已知点C（﹣2，﹣2），点D（2，2），若点P在射线OC和OD上，其限变点Q的纵坐标b的取值范围是b′≥m或b′≤n，其中m＞n，令s＝m﹣n，直接写出s的值．
（3）如图3，若点P在线段EF上，点E（﹣2，﹣5），点F（k，k﹣3），其限变点Q的纵坐标b′的取值范围是﹣2≤b′≤5，直接写出k的取值范围．
37．（2019春?福州期中）在同一平面内，若一个点到一条直线的距离不大于1，则称这个点是该直线的“伴侣点”．
在平面直角坐标系中，已知点M（2，0），过点M作直线l平行于y轴，点A（0，a），点B（b+1，2a），点C（，a﹣1），将△ABC进行平移，平移后点A的对应点为D，点B的对应点为E，点C的对应点为F．
（1）试判断点A是否是直线l的“伴侣点”？　 　（填“是”或者“否”）
（2）若点F刚好落在直线l上，F的纵坐标为a+b，点E落在x轴上，且△MFD的面积为．
①D（　 　，　 　）；E（　 　，　 　）；F（　 　，　 　）（用只含字母a的代数式表示）
②试判断点B是否是直线l的“伴侣点”？并通过计算说明理由．
38．（2018秋?宜宾期末）射线a绕原点O从数轴的正半轴逆时针旋转一定的角度θ（0°≤θ≤360°），射线上的一点N与原点O的距离（ON）为n，并规定：当0°≤θ≤90°或270°≤θ≤360°时，点N的位置记作N（θ，n）；当90°＜θ＜270°时，点N的位置记作N（θ，﹣n）．如图，点S、T的位置表示为S（30°，2.5），T（235°，﹣4）．回答下列问题：
（1）已知点A（70°，3），点B（250°，﹣4），则点A与点B的距离为　 　；线段AB的中点M的位置是（　 　，　 　）．
（2）已知点C（120°，﹣5），点D（300°，6），P（0°，4），点Q从C点出发，以每秒2个单位长度的速度在线段CD上来回运动；同时射线OP以每秒10°的速度绕原点O逆时针旋转，当时间t（其中0≤t≤36）为何值时，OP⊥CD？并求出此时三角形POQ的面积．
（3）直接写出位置满足（θ，5）的所有点所围成的图形面积．（结果保留一位小数）
第四章 图形与坐标培优专题
参考答案与试题解析
一．选择题（共20小题）
1．（2020春?毕节市月考）已知点A的坐标为（1，3），点A向左平移1个单位长度，向下平移4个单位长度．则点A的对应点的坐标为（　　）
A．（5，3） B．（﹣1，﹣2） C．（﹣1，﹣1） D．（0，﹣1）
【答案】D
【解答】解：点P（1，3）向左平移1个单位，再向下平移4个单位所得的对应点的坐标为（1﹣1，3﹣4），即对应点的坐标是（0，﹣1）．
故选：D．
2．（2020?中原区校级模拟）在平面直角坐标系中，若干个半径为1个单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，沿这条曲线向右上下起伏运动，点在直线上的速度为1个单位长度/秒，点在弧线上的速度为个单位长度/秒，则2021秒时，点P的坐标是（　　）
A．（2021，） B．
C． D．（2021，0）
【答案】B
【解答】解：设第n秒运动到Pn（n为自然数）点，
观察，发现规律：
P1（，），P2（1，0），P3（，﹣），P4（2，0），P5（，），…，
∴P4n+1（，），P4n+2（，0），P4n+3（，﹣），P4n+4（，0），
∵2021＝4×505+1，
∴P2021为（，），
故选：B．
3．（2020春?汉阳区校级期中）在平面直角坐标系xOy中，对于点P（x，y），我们把P1（y﹣1，﹣x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，这样依次得到各点．若A2020的坐标为（﹣3，2），设A1（x，y），则x+y的值是（　　）
A．﹣5 B．﹣1 C．3 D．5
【答案】C
【解答】解：假设A1（1，2），则A2（1，﹣2），A3（﹣3，﹣2），A4（﹣3，2），A5（1，2），…，
∴A4n+1（1，2），A4n+2（1，﹣2），A4n+3（﹣3，﹣2），A4n+4（﹣3，2）（n为自然数）．
∵2020＝505×4，
∴A2020的坐标为（﹣3，2），
∴A2021（1，2），A1（1，2），
∴x+y＝3．
故选：C．
4．（2020春?昌图县期末）若将点A（m+2，3）先向下平移1个单位，再向左平移2个单位，得到点B（2，n﹣1）则（　　）
A．m＝2，n＝3 B．m＝2，n＝5 C．m＝﹣6，n＝3 D．m＝﹣6，n＝5
【答案】A
【解答】解：由题意，3﹣1＝n﹣1，m+2﹣2＝2，
解得m＝2，n＝3，
故选：A．
5．（2020春?濮阳期末）如图，已知点A1（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1），…，则点A2020的坐标为（　　）
A．（505，505） B．（506，﹣505）
C．（﹣505，﹣505） D．（﹣505，505）
【答案】C
【解答】解：通过观察可得数字是4的倍数的点在第三象限，
∵2020÷4＝505，
∴点A2020在第三象限，
∴A2020是第三象限的第505个点，
∴点A2020的坐标为：（﹣505，﹣505）．
故选：C．
6．（2020春?岳阳期末）如图，已知正方形ABCD的对角线AC，BD相交于点M，顶点A、B、C的坐标分别为（1，3）、（1，1）、（3，1），规定“把正方形ABCD先沿x轴翻折，再向右平移1个单位”为一次变换，如此这样，连续经过2020次变换后，点M的坐标变为（　　）
A．（2022，2） B．（2022，﹣2） C．（2020，2） D．（2020，﹣2）
【答案】A
【解答】解：∵正方形ABCD，顶点A（1，3），B（1，1），C（3，1），
∴对角线交点M的坐标为（2，2），
根据题意得：第1次变换后的点M的对应点的坐标为（2+1，﹣2），即（3，﹣2），
第2次变换后的点M的对应点的坐标为：（2+2，2），即（4，2），
第3次变换后的点M的对应点的坐标为（2+3，﹣2），即（5，﹣2），
第n次变换后的点M的对应点的坐标为：当n为奇数时为（2+n，﹣2），当n为偶数时为（2+n，2），
∴连续经过2020次变换后，正方形ABCD的对角线交点M的坐标变为（2022，2）．
故选：A．
7．（2020春?罗山县期末）在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，An，…．若点A1的坐标为（2，4），点A2020的坐标为（　　）
A．（﹣3，3） B．（﹣2，﹣2） C．（3，﹣1） D．（2，4）
【答案】C
【解答】解：∵A1的坐标为（2，4），
∴A2（﹣3，3），A3（﹣2，﹣2），A4（3，﹣1），A5（2，4），
…，
依此类推，每4个点为一个循环组依次循环，
∵2020÷4＝505，
∴点A2020的坐标与A4的坐标相同，为（3，﹣1）．
故选：C．
8．（2020春?禹州市期末）在平面直角坐标系中，对于点P（x，y），我们把点P'（1﹣y，x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，…，这样依次得到点A1、A2、A3、A4…，若点A1的坐标为（3，2），则点A2020的坐标为（　　）
A．（3，2） B．（﹣1，2） C．（﹣1，﹣2） D．（3，﹣2）
【答案】D
【解答】解：根据点P（x，y）的友好点是点P'（1﹣y，x﹣1），
点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，
…，
因为点A1的坐标为（3，2），
所以点A2的坐标为（﹣1，2），
点A3的坐标为（﹣1，﹣2），
点A4的坐标为（3，﹣2），
点A5的坐标为（3，2），
…
发现规律：4个点一个循环，
所以2020÷4＝505，
则点A2020的坐标为（3，﹣2）．
故选：D．
9．（2020春?潼南区期末）如图，在平面直角坐标系中，OA1＝1，将边长为1的正方形一边与x轴重合按图中规律摆放，其中相邻两个正方形的间距都是1，则点A2022的坐标为（　　）
A．（1009，1） B．（1010，1） C．（1011，0） D．（1011，﹣1）
【答案】D
【解答】解：由图可得，第一个正方形中，A1（1，0），A2（1，1），A3（2，1），A4（2，0），
各点的横坐标依次为1，1，2，2，纵坐标依次为0，1，1，0；
第二个正方形中，A5（3，0），A6（3，﹣1），A7（4，﹣1），A8（4，0），
各点的横坐标依次为3，3，4，4，纵坐标依次为0，﹣1，﹣1，0；
根据纵坐标的变化规律可知，每8个点一次循环，
∵2016÷8＝252，
∴点A2022在第253个循环中的第6个点的位置，故其纵坐标为﹣1，
又∵A6的横坐标为3，A14的横坐标为7，A22的横坐标为11，
…
∴A2022的横坐标为1011，
∴点A2022的坐标为（1011，﹣1），
故选：D．
10．（2020春?莒县期末）如图，在平面直角坐标系上有点A（1，0），点A第一次跳至点A1（﹣1，1），第二次向右跳动3个单位至点A2（2，1），第三次跳至点A3（﹣2，2），第四次向右跳动5个单位至点A4（3，2），…依此规律跳动下去，点A第100次跳至点A100的坐标是（　　）
A．（50，50） B．（51，50） C．（50，51） D．（49，50）
【答案】B
【解答】解：观察发现，第2次跳动至点的坐标是（2，1），
第4次跳动至点的坐标是（3，2），
第6次跳动至点的坐标是（4，3），
第8次跳动至点的坐标是（5，4），
…
第2n次跳动至点的坐标是（n+1，n），
故第100次跳动至点的坐标是（51，50）．
故选：B．
11．（2020春?巩义市期末）如图，在4×8的长方形网格OABC中，动点P从（0，3）出发，沿箭头所示方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，当点P第2020次碰到矩形的边时，点P的坐标为（　　）
A．（1，4） B．（5，0） C．（6，4） D．（8，3）
【答案】B
【解答】解：如图，根据题意得：P0（0，3），P1（3，0），P2（7，4），P3（8，3），P4（5，0），P5（1，4），P6（0，3），P7（3，0），…，
∴点Pn的坐标6次一循环．经过6次反弹后动点回到出发点（0，3），
∵2020÷6＝336…4，
∴当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹，
点P的坐标为（5，0）．
故选：B．
12．（2020春?龙华区校级期末）在平面直角坐标系中，对于任意三点A、B、C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S＝ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a＝5，“铅垂高”h＝4，“矩面积”S＝ah＝20，若D（1，2）、E（﹣2，1）、F（0，t）三点的“矩面积”为15，则t的值为（　　）
A．﹣3或7 B．﹣4或6 C．﹣4或7 D．﹣3或6
【答案】D
【解答】解：∵D（1，2）、E（﹣2，1）、F（0，t），
∴“水平底”a＝1﹣（﹣2）＝3．
“铅垂高“h＝1或|2﹣t|或|1﹣t|
①当h＝1时，三点的“矩面积”S＝1×3＝3≠15，不合题意；
②当h＝|2﹣t|时，三点的“矩面积”S＝3×|2﹣t|＝15，
解得：t＝﹣3或t＝7（舍去）；
③当h＝|1﹣t|时，三点的“矩面积”S＝3×|1﹣t|＝15，
解得：t＝﹣4（舍去）或t＝6；
综上：t＝﹣3或6．
故选：D．
13．（2020春?建安区期末）如图，平面直角坐标系中，一蚂蚁从A点出发，沿着A→B→C→D→A…循环爬行，其中A点的坐标为（2，﹣2），B点的坐标为（﹣2，﹣2），C点的坐标为（﹣2，6），D点的坐标为（2，6），当蚂蚁爬了2020个单位时，蚂蚁所处位置的坐标为（　　）
A．（﹣2，﹣2） B．（2，﹣2） C．（﹣2，6） D．（0，﹣2）
【答案】A
【解答】解：∵A点坐标为（2，﹣2），B点坐标为（﹣2，﹣2），C点坐标为（﹣2，6），
∴AB＝2﹣（﹣2）＝4，BC＝6﹣（﹣2）＝8，
∴从A→B→C→D→A一圈的长度为2（AB+BC）＝24．
∵2020＝84×24+4，
∴当蚂蚁爬了2020个单位时，它所处位置在点A左边4个单位长度处，即（﹣2，﹣2）．
故选：A．
14．（2020春?思明区校级期末）在平面直角坐标系中，将A （m2，1）沿着x的正方向向右平移m2+3个单位后得到B点．有四个点M（﹣m2，1）、N（m2，m2+3）、P（m2+2，1）、Q（3m2，1），一定在线段AB上的是（　　）
A．点M B．点N C．点P D．点Q
【答案】C
【解答】解：∵将A （m2，1）沿着x的正方向向右平移m2+3个单位后得到B点，
∴B（2m2+3，1），
∵m2≥0，
∴2m2+3＞0，
∴线段AB在第一象限，点B在点A右侧，且与x轴平行，距离x轴1个单位，
因为点M（﹣m2，1）在点A左侧，不在线段AB上；
点N（m2，m2+3）距离x轴（m2+3）个单位，不在线段AB上；
点P（m2+2，1）在点A右侧，且距离x轴1个单位，在线段AB上；
点Q（3m2，1）是将A （m2，1）沿着x的正方向向右平移2m2个单位后得到的，不一定在线段AB上，有可能在线段AB延长线上．
所以一定在线段AB上的是点P．
故选：C．
15．（2020?西华县二模）如图，在平面直角坐标系中，四边形OABC关于x轴对称，∠AOC＝60°，∠ABC＝90°，OA＝2，将四边形OABC绕点O逆时针旋转90°后得到四边形OA1B1C1，依此方式，绕点O连续旋转71次得到四边形OA71B71C71，那么点B71的坐标是（　　）
A． B．（3，0） C． D．（﹣3，0）
【答案】C
【解答】解：连接AC交OB于E．
由题意，OA＝OC＝2，∠AOC＝60°，∠ABC＝90°，
∵四边形AOCB关于x轴对称，
∴∠AOE＝30°，∠ABE＝45°，
∴OE＝OA?cos30°＝．AE＝EB＝OA?sin30°＝1，
∴B（+1，0），B1（0，+1），B2（﹣﹣1，0），B3（0，﹣﹣1），
观察图象可知，4次一个循环，
∵71÷4＝17…3，
∴B71的坐标与B3相同，
故选：C．
16．（2020春?永川区期末）如图，在平面直角坐标系中，有若干个整数点，其顺序按图中方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），……，根据这个规律探索可得，第120个点的坐标为（　　）
A．（16，0） B．（15，14） C．（15，0） D．（14，13）
【答案】C
【解答】解：把第一个点（1，0）作为第一列，（2，1）和（2，0）作为第二列，依此类推，则第一列有一个数，第二列有2个数，…，第n列有n个数．则n列共有个数，并且在奇数列点的顺序是由上到下，偶数列点的顺序由下到上．
因为120＝1+2+3+…+14+15，则第120个数一定在第15列，由下到上是第1个数．因而第120个点的坐标是（15，0）．
故选：C．
17．（2020春?重庆期末）如图，一个点在第一象限及x轴、y轴上移动，在第一秒钟，它从原点移动到点（1，0），然后按照图中箭头所示方向移动，即（0，0）→（1，0）→（1，1）→（0，1）→（0，2）→…，且每秒移动一个单位，那么第2020秒时，点所在位置的坐标是（　　）
A．（64，44） B．（45，5） C．（44，5） D．（44，4）
【答案】D
【解答】解：观察可发现，点到（0，2）用4＝22秒，到（3，0）用9＝32秒，到（0，4）用16＝42秒，
则可知当点离开x轴时的横坐标为时间的平方，当点离开y轴时的纵坐标为时间的平方，
此时时间为奇数的点在x轴上，时间为偶数的点在y轴上
∵2020＝452﹣5＝2025﹣5，
∴第2025秒时，动点在（45，0），故第2020秒时，动点在（45，0）向左一个单位，再向上4个单位，
即（44，4）的位置．
故选：D．
18．（2020春?南召县期末）如图，在平面直角坐标系中有一边长为1的正方形OABC，边OA，OC分别在x轴、y轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，照此规律作下去，则点B2020的坐标为（　　）
A．（﹣21010，21010） B．（22020，﹣22020）
C．（﹣22020，﹣22020） D．（﹣21010，﹣21010）
【答案】D
【解答】解：∵正方形OABC边长为1，
∴OB＝，
∵正方形OBB1C1是正方形OABC的对角线OB为边，
∴OB1＝2，
∴B1点坐标为（0，2），
同理可知OB2＝2，
∴B2点坐标为（﹣2，2），
同理可知OB3＝4，B3点坐标为（﹣4，0），
B4点坐标为（﹣4，﹣4），B5点坐标为（0，﹣8），
B6（8，﹣8），B7（16，0）
B8（16，16），B9（0，32），
由规律可以发现，每经过8次作图后，点的坐标符号与第一次坐标符号相同，每次正方形的边长变为原来的倍，
∵2020÷8＝252…4，
∴B2020的横纵坐标符号与点B4相同，横纵坐标相同，且都在第三象限，
∴B2020的坐标为（﹣21010，﹣21010）．
故选：D．
19．（2020春?武鸣区校级期中）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），那么A2020坐标为（　　）
A．（2020，1） B．（2020，0） C．（1010，1） D．（1010，0）
【答案】D
【解答】解：由图象可知：纵坐标每四个点循环一次，而2020＝505×4，
故A2020的纵坐标与A4的纵坐标相同，都等于0；
由A4（2，0），A8（4，0），A12（6，0）…，
可得到规律A4n（2n，0）（n为不为0的自然数），
当n＝505时，A2020（1010，0）．
故选：D．
20．（2020?河南一模）已知点E（x0，yo），点F（x2，y2），点M（x1，y1）是线段EF的中点，则x1＝，y1＝．在平面直角坐标系中有三个点A（1，﹣1），B（﹣1，﹣1），C（0，1），点P（0，2）关于点A的对称点P1（即P，A，P1三点共线，且PA＝P1A），P1关于点B的对称点P2，P2关于点C的对称点P3，…按此规律继续以A，B，C三点为对称点重复前面的操作．依次得到点P4，P5，P6…，则点P2020的坐标是（　　）
A．（4，0） B．（﹣2，﹣2） C．（2，﹣4） D．（﹣4，2）
【答案】B
【解答】解：∵A（1，﹣1），B（﹣1，﹣1），C（0，1），
点P（0，2）关于点A的对称点P1，
∴1＝，﹣1＝，
解得x＝2，y＝﹣4，
所以点P1 （2，﹣4）；
同理：
P1关于点B的对称点P2，
所以P2 （﹣4，2）
P2关于点C的对称点P3，
所以P3 （4，0），
P4（﹣2，﹣2），
P5（0，0），
P6 （0，2），
…，
发现规律：
每6个点一组为一个循环，
∴2020÷6＝336…4，
所以P2020与P4重合，
所以点P2020的坐标是（﹣2，﹣2）．
故选：B．
二．填空题（共10小题）
21．（2020春?崇川区校级期中）在平面直角坐标系中，将点P（2，﹣3）先向上平移1个单位长度，再向左平移3个单位长度后，得到点P′，则点P′的坐标为　（﹣1，﹣2）　．
【答案】（﹣1，﹣2）．
【解答】解：平移后点Q的坐标为（2﹣3，﹣3+1），即（﹣1，﹣2），
故答案为：（﹣1，﹣2）．
22．（2020春?谢家集区期末）如图，在平面直角坐标系中，线段AB在x轴上，将线段AB向上平移2个单位．再向右平移1个单位，得到线段CD，连接AC，BD，在y轴上存在点P，使△PCD的面积为四边形ABDC面积的一半，则点P的坐标为　（0，0）或（0，4）　．
【答案】（0，0）或（0，4）．
【解答】解：由平移可得，C（0，2），D（4，2），
∴CD＝AB＝4，CD∥AB，
∴四边形ABCD为平行四边形，
∴四边形ABCD面积＝4×2＝8，
又∵△PCD的面积为四边形ABCD面积的一半，
∴△PCD的面积为4，
即×CD×CP＝4，
∴CP＝2，
∴当点P在CD下方时，P（0，0）；当点P在CD上方时，P（0，4），
故答案为：（0，0）或（0，4）．
23．（2020春?市中区校级期中）在平面直角坐标系中，△OAB的位置如图所示，将△OAB绕点O顺时针旋转90°得△OA1B1；再将△OA1B1绕点O顺时针旋转90°得△OA2B2；再将△OA2B2绕点O顺时针旋转90°得△OA3B3；……依此类推，第2020次旋转得到△OA2020B2020，则项点A的对应点A2020的坐标是　（1，2）　．
【答案】见试题解答内容
【解答】解：将△OAB绕点O顺时针旋转90°得△OA1B1；此时，点A1的坐标为（2，﹣1）；
再将△OA1B1绕点O顺时针旋转90°得△OA2B2；此时，点A2的坐标为（﹣1，2）；
再将△OA2B2绕点O顺时针旋转90°得△OA3B3；此时，点A3的坐标为（﹣2，1）；
再将△OA3B3绕点O顺时针旋转90°得△OA4B4；此时，点A4的坐标为（1，2）；
∴每旋转4次一个循环，
∵2020÷4＝505，
∴第2020次旋转得到△OA2020B2020，则顶点A的对应点A2020的坐标与点A4的坐标相同，为（1，2）；
故答案为：（1，2）．
24．在平面直角坐标系中，对于点P（a，b），我们把Q（﹣b+1，a+1）叫做点P的伴随点，已知A1的伴随点为A2，A2的伴随点为A3，…，这样依次下去得到A1，A2，A3，…，An，若A1的坐标为（3，1），则A2020的坐标为　（0，﹣2）　．
【答案】（0，﹣2）．
【解答】解：∵点A1的坐标为（3，1），
∴A2的坐标为（0，4），
A3的坐标为（﹣3，1），
A4的坐标为（0，﹣2），
A5的坐标为（3，1），
∴每连续的四个点一个循环，
∵2020÷4＝505，
∴A2020的坐标为（0，﹣2），
故答案为：（0，﹣2）．
25．（2020春?郯城县期末）如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2021秒时，点P的坐标是　（2021，1）　．
【答案】（2021，1）．
【解答】解：半径为1个单位长度的半圆的周长为×2π×1＝π，
∵点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，
∴点P每秒走个半圆，
当点P从原点O出发，沿这条曲线向右运动，运动时间为1秒时，点P的坐标为（1，1），
当点P从原点O出发，沿这条曲线向右运动，运动时间为2秒时，点P的坐标为（2，0），
当点P从原点O出发，沿这条曲线向右运动，运动时间为3秒时，点P的坐标为（3，﹣1），
当点P从原点O出发，沿这条曲线向右运动，运动时间为4秒时，点P的坐标为（4，0），
当点P从原点O出发，沿这条曲线向右运动，运动时间为5秒时，点P的坐标为（5，1），
当点P从原点O出发，沿这条曲线向右运动，运动时间为6秒时，点P的坐标为（6，0），
…，
∵2021÷4＝505余1，
∴P的坐标是（2021，1），
故答案为：（2021，1）．
26．（2020春?抚顺县期末）如图，在平面直角坐标系中，一动点从原点O出发，按向上﹣向右﹣向下﹣向右的方向依次平移，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A2020的坐标为　（1010，0）　．
【答案】（1010，0）．
【解答】解：∵2020÷4＝505，
则A2020的坐标是（505×2，0）＝（1010，0）．
故答案为：（1010，0）．
27．（2020春?禹城市期末）如图，在平面直角坐标系中，将△ABC绕点A顺时针旋转到△A1B1C1的位置，点B，O（分别落在点B1，C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，再将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去，…，若点A（，0），B（0，2），则点B2020的坐标为　（6060，2）　．
【答案】见试题解答内容
【解答】解：∵AO＝，BO＝2，
∴AB＝＝＝，
∴OA+AB1+B1C2＝++2＝6，
∴B2的横坐标为：6，且B2C2＝2，
∴B4的横坐标为：2×6＝12，
∴点B2020的横坐标为：1010×6＝6060．
∴点B2020的纵坐标为：2．
故答案为：（6060，2）．
28．（2020?新昌县模拟）在平面直角坐标系中，如果一个图形向右平移1个单位，再向上平移3个单位，称为一个变换，已知点A（1，﹣2），经过一个变换后对应点为A1，经过2个变换后对应点为A2，…经过n个变换后对应点为An，则用含n的代数式表示点An的坐标为　（1+n，﹣2+3n）　．
【答案】见试题解答内容
【解答】解：∵如果一个图形向右平移1个单位，再向上平移3个单位，称为一个变换，
∴点A（1，﹣2）经过一个变换后对应点A1的坐标为（2，1），
经过2个变换后对应点为A2的坐标为（3，4），
经过3个变换后对应点为A3的坐标为（4，7），
∴经过n个变换后对应点An的坐标为（1+n，﹣2+3n），
故答案为：（1+n，﹣2+3n）．
29．（2020春?博兴县期末）如图，动点P在平面直角坐标系中按箭头所示方向做折线运动，即第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1），…．按这样的运动规律，经过第2020次运动后，动点P的坐标是　（2020，0）　．
【答案】见试题解答内容
【解答】解：∵第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1），…，
∴按这样的运动规律，第几次横坐标即为几，纵坐标为：1，0，2，0，1，0，2，0，…，4个一循环，
∵2020÷4＝505，
∴经过第2020次运动后，动点P的坐标是（2020，0）．
故答案为：（2020，0）．
30．（2020春?江汉区期末）如图，在平面直角坐标系中，有若干个横坐标和纵坐标分别为整数的点，其顺序按图中“→”方向排列，第1个点为（1，0），后面依次为（2，0），（1，2），（1，3），（2，2），（3，0）…，根据这个规律，第110个点的坐标为　（5，10）　．
【答案】（5，10）．
【解答】解：从直角三角形斜边考虑，斜边上的点的个数分别为1、2、3、4、…，
所以点的总个数为：
1+2+3+4+…+n＝，
当n＝14时，＝105，
所以第110个点是当n＝15时的第5个点，
即第15个斜边上点为：
（1，14），（2，13），（3，12），（4，11），（5，10）…
所以第110个点的坐标为（5，10）．
故答案为（5，10）．
三．解答题（共9小题）
31．（2020春?开福区校级期中）如图，△ABC向左平移3个单位，再向上平移1个单位得到△A1B1C1．已知A（2，1），B（5，3），C（3，4）．
（1）直接写出△A1B1C1三个顶点的坐标；
（2）求△ABC的面积．
【答案】（1）A1（﹣1，2），B1（2，4），C1（0，5）．
（2）．
【解答】解：（1）如图，△A1B1C1即为所求，A1（﹣1，2），B1（2，4），C1（0，5）．
（2）S△ABC＝3×3﹣×1×2﹣×3×1﹣×3×2＝．
32．（2020春?西乡塘区校级月考）已知点A（a﹣1，﹣2），B（﹣3，b+1），根据以下要求确定a，b的值．
（1）当直线AB∥x轴时，a　≠﹣2　，b　＝﹣3　；
（2）当直线AB∥y轴时，a　＝﹣2　，b　≠﹣3　；
（3）当点A和点B在二四象限的角平分线上时，求a，b的值．
【答案】（1）≠﹣2，﹣3；
（2）﹣2，≠﹣3；
（3）a＝3，b＝2．
【解答】解：（1）∵直线AB∥x轴，
∴点A与点B的纵坐标相同，
∴b+1＝﹣2，
∴b＝﹣3，
∵AB是直线，
∴A，B不重合，
∴a﹣1≠﹣3，
解得：a≠﹣2，
故答案是：≠﹣2，＝﹣3；
（2）∵直线AB∥y轴，
∴点A与点B的横坐标相同，A，B点纵坐标不相等，
∴a﹣1＝﹣3，﹣2≠b+1，
∴a＝﹣2，b≠﹣3；
故答案是：＝﹣2，≠﹣3；
（3）∵A、B两点在第二、四象限的角平分线上，
∴a﹣1+（﹣2）＝0，b+1+（﹣3）＝0，
∴a＝3，b＝2．
33．（2020秋?滨州月考）如图，在平面直角坐标系中，图中的网格是由边长相等的小正方组成，点A、B、C的坐标分别为（﹣5，4），（﹣4，0）．（﹣5，﹣3）．
（1）请写出点D、E、F、G的坐标；
（2）求图中阴影部分（多边形ABCDEFG）的面积．
【答案】见试题解答内容
【解答】解：（1）点D、E、F、G的坐标分别为：（0，﹣2）、（5，﹣3）、（3，4）、（﹣1，2）；
（2）阴影部分（多边形ABCDEFG）的面积为：
[5﹣（﹣5）]×[4﹣（﹣3）]﹣[4﹣（﹣3）]×1÷2﹣[3﹣（﹣5）]×2÷2﹣2×[4﹣（﹣3）]÷2﹣[5﹣（﹣5）]×1÷2
＝10×7﹣3.5﹣8﹣7﹣5
＝70﹣23.5
＝46.5．
∴阴影部分（多边形ABCDEFG）的面积为46.5．
34．（2020春?渝水区校级月考）如图，在平面直角坐标系中，点A、B在坐标轴上，其中A（0，a）、B（b，0）满足：
（1）求A、B两点的坐标；
（2）将线段AB平移到CD，点A的对应点为C（﹣2，t），若三角形ABC的面积为8，求点D的坐标．
【答案】（1）A（0，2），B（3，0）；
（2）（1，﹣4）．
【解答】解：（1）∵|2a﹣b﹣1|+＝0，
又∵：|2a﹣b﹣1|≥0，≥0，
∴，
解得，
∴A（0，2），B（3，0）；
（2）如图1中，设直线CD交y轴于E．
∵CD∥AB，
∴S△ACB＝S△ABE，
∴×AE×BO＝8，
∴×AE×3＝8，
∴AE＝，
∴E（0，﹣），
设直线AB的解析式为y＝kx+2，
把B（3，0）坐标代入得k＝﹣
∵直线AB的解析式为y＝﹣x+2，
∴直线CD的解析式为y＝﹣x﹣，
把C（﹣2，t）代入y＝﹣x﹣得到t＝﹣2，
∴C（﹣2，﹣2），
将点C向下平移2个单位，向右平移3个单位得到点D，
∴D（1，﹣4）．
35．（2020秋?雨花区校级月考）在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“近似距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1（x1，y1）与点P2（x2，y2）的“近似距离”为|x1﹣x2|；若|x1﹣x2|＜|y1﹣y2|，则P1（x1，y1）与点P2（x2，y2）的“近似距离”为|y1﹣y2|；
（1）已知点P（﹣3，4）、点Q（1，1），则点P与点Q的“近似距离”为　4　．
（2）已知点A（0，﹣2），B为x轴上的动点，
①若点A与B的“近似距离为3”，写出满足条件的B点的坐标　（3，0）、（﹣3，0）　．
②直接写出点A与点B的“近似距离”的最小值　2　．
（3）已知C（2m+2，m），D（1，0），写出点C与点D的“近似距离”的最小值及相应的C点坐标．
【答案】（1）4；
（2）①（3，0）或（﹣3，0）；②2；
（3），（，﹣）．
【解答】解：（1）∵点P（﹣3，4）、点Q（1，1），
则点P与点Q的“近似距离”为4．
故答案为：4；
（2）①∵B为x轴上的一个动点，
∴设点B的坐标为（x，0）．
∵A、B两点的“近似距离为3”，A（0，﹣2），
∵|0﹣x|＝3，|﹣2﹣0|＝2，
解得x＝3或x＝﹣3，
∴点B的坐标是（3，0）或（﹣3，0），
故答案为：（3，0）或（﹣3，0）；
②∵设点B的坐标为（x，0），且A（0，﹣2），
∴|﹣2﹣0|＝2，|0﹣x|＝x，
∴若|﹣2﹣0|＜|0﹣x|，则点A、B两点的“近似距离”为|x|＞2，
若|﹣2﹣0|≥|0﹣x|，则点A、B两点的“近似距离”为|﹣2﹣0|＝2；
∴A、B两点的“近似距离”的最小值为2，
故答案为：2；
（3）∵C（2m+2，m），D（1，0），
∴|2m+2﹣1|＝|m﹣0|＝|2m+1|，
当m＞0时，m＝2m+1，
解得：m＝﹣1（舍去）；
当﹣＜m＜0时，﹣m＝2m+1，
解得：m＝﹣；
∴点C与D的“近似距离”的最小值为|m|＝；相应的C点坐标为（，﹣）；
答：点C与D的“近似距离”的最小值及相应的C点坐标为：，（，﹣）．
36．（2020春?海淀区校级期末）在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
若b′＝，则称点Q为点P的限变点．例如：点（2，3）的限变点的坐标是（2，2），点（﹣2，﹣5）的限变点的坐标是（﹣2，5），点（1，3）的限变点的坐标是（1，3）．
（1）①点（，﹣1）的限变点的坐标是　（，1）　；
②如图1，在点A（﹣2，1）、B（2，1）中有一个点是直线y＝2上某一个点的限变点，这个点是　B　；（填“A”或“B”）
（2）如图2，已知点C（﹣2，﹣2），点D（2，2），若点P在射线OC和OD上，其限变点Q的纵坐标b的取值范围是b′≥m或b′≤n，其中m＞n，令s＝m﹣n，直接写出s的值．
（3）如图3，若点P在线段EF上，点E（﹣2，﹣5），点F（k，k﹣3），其限变点Q的纵坐标b′的取值范围是﹣2≤b′≤5，直接写出k的取值范围．
【答案】（1）①（，1），②B；
（2）s＝3；
（3）5≤k≤9．
【解答】（1）①∵a＝＜2，
∴b′＝|b|＝|﹣1|＝1，
∴坐标为（，1）．
故答案为（，1）．
②s＝3．
∵对于限变点来说，横坐标保持不变，
∴限变点A（﹣2，1）对应的原来点的坐标为：（﹣2，1）或（﹣2，﹣1），
限变点B（2，1]对应的原来点的坐标为：（2.2），
∵（2，2）满足y＝2，
∴这个点是B，
故答案为：B；
（ 2）∵点C的坐标为（﹣2，﹣2），
∴OC的关系式为：y＝x（x≤0），
∵点D的坐标为（2，﹣2），
∴OD的关系式为：y＝﹣x（x≥0），
∴点P满足的关系式为：y＝，
当x≥2时：b'＝一x﹣1，
当0＜x＜2时：b'＝﹣x﹣1，
当x≤0时，b＝|x|＝﹣x，
图象如图1所示，
通过图象可以得出：当x≥2时，b'≤﹣3，n＝﹣3，
当x＜2时，b'≥0，
∴m＝0，
∴s＝m﹣n＝0﹣（﹣3）＝3；
（3）设线段E的关系式为：y＝ax+c（a≠0，﹣2≤x≤k，k＞﹣2），
把E（﹣2，﹣5），F（k，k﹣3）代入，
得，
解得，
∴线段EP的关系式为y＝x一3（﹣2≤x≤k，k＞﹣2），
∴线段E上的点P的限变点Q的纵坐标满足的关系式b'＝
，
图象如图2所示：
当x＝2时，b'取最小值，b'＝2﹣4＝﹣2，
当b'＝5时，
x﹣4＝5或﹣x+3＝5，解得：x＝9或x＝﹣2，
当b'＝1时，
x﹣4＝1，解得：x＝5，
∵﹣2≤b'＜5，
∴由图象可知，k的取值范围是：5≤k≤9．
37．（2019春?福州期中）在同一平面内，若一个点到一条直线的距离不大于1，则称这个点是该直线的“伴侣点”．
在平面直角坐标系中，已知点M（2，0），过点M作直线l平行于y轴，点A（0，a），点B（b+1，2a），点C（，a﹣1），将△ABC进行平移，平移后点A的对应点为D，点B的对应点为E，点C的对应点为F．
（1）试判断点A是否是直线l的“伴侣点”？　否　（填“是”或者“否”）
（2）若点F刚好落在直线l上，F的纵坐标为a+b，点E落在x轴上，且△MFD的面积为．
①D（　　，　a+b+1　）；E（　b+　，　2a+b+1　）；F（　2　，　a+b　）（用只含字母a的代数式表示）
②试判断点B是否是直线l的“伴侣点”？并通过计算说明理由．
【答案】见试题解答内容
【解答】解：（1）∵A（0，a），直线l：x＝2，
∴点A到直线l的距离为2，2＞1，
∴点A不是直线l的“伴侣点”，
故答案为：否；
（2）①∵C（，a﹣1）→F（2，a+b），
∴横坐标加，纵坐标加（b+1），
∴D（，a+b+1），E（b+，2a+b+1）；
故答案为：，a+b+1；b+，2a+b+1，2，a+b；
②∵点E落在x轴上，
∴2a+b+1＝0，
∵三角形MFD的面积为，
∴??|a+b|＝，
∴a+b＝±，
当a+b＝时，解得a＝﹣，b＝，此时B（，﹣），点B是直线l的“伴侣点”．
当a+b＝﹣时，a＝﹣，b＝，此时B（，﹣），点B是直线l的“伴侣点”．
38．（2018秋?宜宾期末）射线a绕原点O从数轴的正半轴逆时针旋转一定的角度θ（0°≤θ≤360°），射线上的一点N与原点O的距离（ON）为n，并规定：当0°≤θ≤90°或270°≤θ≤360°时，点N的位置记作N（θ，n）；当90°＜θ＜270°时，点N的位置记作N（θ，﹣n）．如图，点S、T的位置表示为S（30°，2.5），T（235°，﹣4）．回答下列问题：
（1）已知点A（70°，3），点B（250°，﹣4），则点A与点B的距离为　7　；线段AB的中点M的位置是（　250°　，　﹣0.5　）．
（2）已知点C（120°，﹣5），点D（300°，6），P（0°，4），点Q从C点出发，以每秒2个单位长度的速度在线段CD上来回运动；同时射线OP以每秒10°的速度绕原点O逆时针旋转，当时间t（其中0≤t≤36）为何值时，OP⊥CD？并求出此时三角形POQ的面积．
（3）直接写出位置满足（θ，5）的所有点所围成的图形面积．（结果保留一位小数）
【答案】见试题解答内容
【解答】解：（1）∵点A（70°，3），点B（250°，﹣4），
可得，点A，点O，点B在同一直线上，
∴AB＝2+4＝7，
AB的中点位置为（250°，﹣0.5），
故答案为7，（250°，﹣0.5）
（2）当OP逆时针旋转30°时，OP⊥CD．此时，秒
点Q移动的长度为：2×3＝6，
∴OQ＝1
∴．
当OP逆时针旋转210°时，OP⊥CD．此时，秒
点Q移动的长度为：2×21＝42，
∴OQ＝3，
∴．
（3）由题意：位置满足（θ，5）的所有点所围成的图形面积是半径为5的半圆的面积＝?π?52≈39.3．
_21?????????è?????(www.21cnjy.com)_