5.4 一次函数的图像同步培优练习(含解析)
文档属性
| 名称 | 5.4 一次函数的图像同步培优练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 20:46:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.4一次函数的图像
一.选择题(共10小题)
1.(2020秋?九龙坡区校级月考)若一次函数y=kx+b的图象经过点(4,2)、(2,﹣2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.6
B.9
C.12
D.18
2.(2020春?南充期末)一次函数y=kx+b的图象如图所示,则下列说法:①kb>0;②若点A(﹣2,m)与B(3,n)都在直线y=kx+b上,则m>n;③当x>0时,y>b.其中正确的说法是( )
A.①②
B.①③
C.②③
D.①②③
3.(2020春?东坡区期末)在平面直角坐标系中,一次函数y=kx﹣3(k<0)的图象大致是( )
A.
B.
C.
D.
4.(2020?凉山州)若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是( )
A.m>﹣
B.m<3
C.﹣<m<3
D.﹣<m≤3
5.(2020春?丛台区校级期中)直线l:y=(m﹣3)x+n﹣2(m,n为常数)图象如图,化简|m﹣3|﹣的结果为( )
A.5﹣m﹣n
B.5
C.﹣1
D.m+n﹣5
6.(2020?邗江区校级一模)一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是( )
A.﹣3<x<0
B.x<0
C.﹣3<x<2
D.x>﹣3
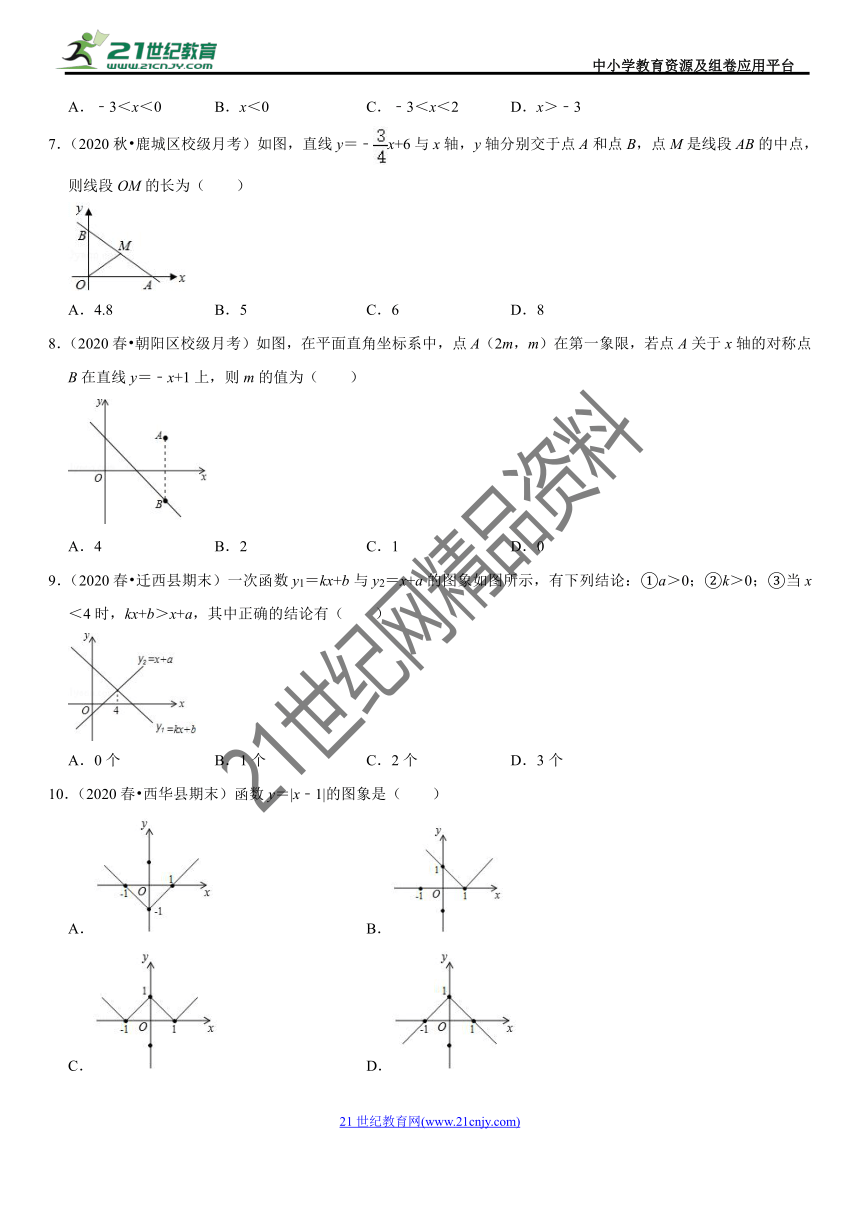
7.(2020秋?鹿城区校级月考)如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8
B.5
C.6
D.8
8.(2020春?朝阳区校级月考)如图,在平面直角坐标系中,点A(2m,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.4
B.2
C.1
D.0
9.(2020春?迁西县期末)一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①a>0;②k>0;③当x<4时,kx+b>x+a,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
10.(2020春?西华县期末)函数y=|x﹣1|的图象是( )
A.
B.
C.
D.
二.填空题(共8小题)
11.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是
(写出一个答案即可).
12.(2020春?营山县期末)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为
.
13.(2019秋?中原区校级期中)如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是
.
14.(2020春?成华区期末)如图,在平面直角坐标系中,已知点A(4,0),B(0,5).将△BOA绕点A顺时针方向旋转得△B′O′A,若点B在B′O′的延长线上,则直线BB′的解析式为
.
15.(2019秋?温州期末)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,与y轴交于点B,点P在线段AB上,PC⊥x轴于点C,则△PCO周长的最小值为
.
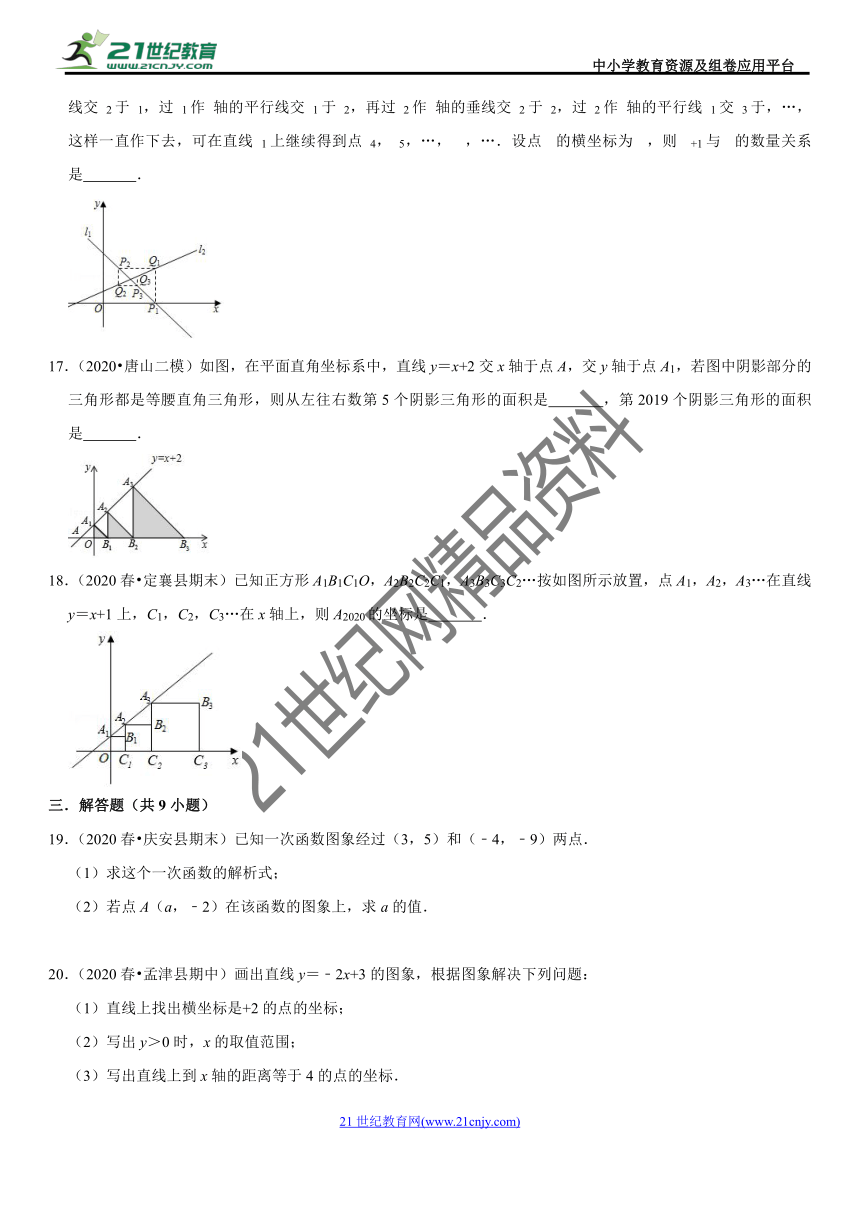
16.(2020春?海淀区校级月考)如图,已知直线l1:y=﹣x+2与l2:y=x+,过直线????1与????轴的交点????1作????轴的垂线交????2于????1,过????1作????轴的平行线交????1于????2,再过????2作????轴的垂线交????2于????2,过????2作????轴的平行线????1交????3于,…,这样一直作下去,可在直线????1上继续得到点????4,????5,…,????????,….设点????????的横坐标为????????,则????????+1与????????的数量关系是
.
17.(2020?唐山二模)如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是
,第2019个阴影三角形的面积是
.
18.(2020春?定襄县期末)已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则A2020的坐标是
.
三.解答题(共9小题)
19.(2020春?庆安县期末)已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求这个一次函数的解析式;
(2)若点A(a,﹣2)在该函数的图象上,求a的值.
20.(2020春?孟津县期中)画出直线y=﹣2x+3的图象,根据图象解决下列问题:
(1)直线上找出横坐标是+2的点的坐标;
(2)写出y>0时,x的取值范围;
(3)写出直线上到x轴的距离等于4的点的坐标.
21.(2020秋?渝中区校级月考)如图,已知一次函数y=x+3的图象分别与x轴、y轴交于点A、点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)若点P是x轴上的动点,且S△BOP=S△ABC,求符合条件的点P的坐标.
22.(2020春?三台县期末)已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设△OBA的面积为S.
(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=12时B点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.
23.(2019秋?成华区期末)如图,一次函数y=kx+b的图象经过点A
(﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
24.(2019秋?新泰市期末)两个一次函数l1、l2的图象如图:
(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
25.(2019春?历城区期中)探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为
.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y=x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
26.(2019秋?雨城区校级期中)如图,已知直线c和直线b相交于点(2,2),直线c过点(0,3).平行于y轴的动直线a的解析式为x=t,且动直线a分别交直线b、c于点D、E(E在D的上方).
(1)求直线b和直线c的解析式;
(2)若P是y轴上一个动点,且满足△PDE是等腰直角三角形,求点P的坐标.
27.(2018秋?九龙坡区校级期末)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点A(0,6),tan∠OBA=,直线OC与直线l1点相交于点C,且S△BOC=6.
(1)求直线l1的解析式和点C的坐标;
(2)点D是点B关于y轴的对称点,将直线OC沿y轴向下平移,记为直线l2,若直线l2经过点D,与直线l1交于点E,求△ADE的面积.
5.4一次函数的图像
参考答案与试题解析
一.选择题(共10小题)
1.(2020秋?九龙坡区校级月考)若一次函数y=kx+b的图象经过点(4,2)、(2,﹣2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.6
B.9
C.12
D.18
【答案】B
【解答】解:将(4,2),(2,﹣2)代入y=kx+b,得:,
解得:,
∴一次函数的解析式为y=2x﹣6.
当x=0时,y=2×0﹣6=﹣6,
∴一次函数y=2x﹣6与y轴的交点坐标为(0,﹣6);
当y=0时,2x﹣6=0,解得:x=3,
∴一次函数y=2x﹣6与x轴的交点坐标为(3,0).
∴一次函数y=2x﹣6与两坐标轴围成的三角形的面积=×6×3=9.
故选:B.
2.(2020春?南充期末)一次函数y=kx+b的图象如图所示,则下列说法:①kb>0;②若点A(﹣2,m)与B(3,n)都在直线y=kx+b上,则m>n;③当x>0时,y>b.其中正确的说法是( )
A.①②
B.①③
C.②③
D.①②③
【答案】B
【解答】解:①∵图象过第一,第二,第三象限,
∴k>0,b>0,
∴kb>0正确,符合题意;
②由①知,y随x增大而增大,
∵﹣2<3,故m<n,
故②错误,不符合题意;
③当x=0时,y=kx+b=b,
∴当x>0时,从图象看,y>b正确,符合题意;
故选:B.
3.(2020春?东坡区期末)在平面直角坐标系中,一次函数y=kx﹣3(k<0)的图象大致是( )
A.
B.
C.
D.
【答案】C
【解答】解:∵一次函数y=kx﹣3(k<0),b=﹣3,
∴该函数图象经过第二、三、四象限,
故选:C.
4.(2020?凉山州)若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是( )
A.m>﹣
B.m<3
C.﹣<m<3
D.﹣<m≤3
【答案】D
【解答】解:根据题意得,
解得﹣<m≤3.
故选:D.
5.(2020春?丛台区校级期中)直线l:y=(m﹣3)x+n﹣2(m,n为常数)图象如图,化简|m﹣3|﹣的结果为( )
A.5﹣m﹣n
B.5
C.﹣1
D.m+n﹣5
【答案】A
【解答】解:∵直线l:y=(m﹣3)x﹣2+n(m,n为常数)的图象过第一、二、四象限,
∴m﹣3<0,n﹣2>0,
∴|m﹣3|﹣
=3﹣m﹣|n﹣2|
=3﹣m﹣(n﹣2)
=3﹣m﹣n+2
=5﹣m﹣n.
故选:A.
6.(2020?邗江区校级一模)一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是( )
A.﹣3<x<0
B.x<0
C.﹣3<x<2
D.x>﹣3
【答案】A
【解答】解:函数图象如图所示,函数图象在第二象限时,自变量x的取值范围是﹣3<x<0.
故选:A.
7.(2020秋?鹿城区校级月考)如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8
B.5
C.6
D.8
【答案】B
【解答】解:把x=0代入y=﹣x+6得:
y=6,
即点B的坐标为(0,6),
把y=0代入y=﹣x+6得:
﹣x+6=0,
解得:x=8,
即点A的坐标为(8,0),
∴AB==10,
∵点M是线段AB的中点,
∴OM=AB=5,
故选:B.
8.(2020春?朝阳区校级月考)如图,在平面直角坐标系中,点A(2m,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.4
B.2
C.1
D.0
【答案】C
【解答】解:∵点A(2m,m)在第一象限,若点A关于x轴的对称点为点B,
∴B(2m,﹣m),
∵点B在直线y=﹣x+1上,
∴﹣m=﹣2m+1,
∴m=1,
故选:C.
9.(2020春?迁西县期末)一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①a>0;②k>0;③当x<4时,kx+b>x+a,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
【答案】B
【解答】解:①∵y2=x+a的图象与y轴的交点在负半轴上,
∴a<0,
故①错误;
②∵y1=kx+b的图象从左向右呈下降趋势,
∴k<0,故②错误;
③两函数图象的交点横坐标为4,
当x<4时,y1=kx+b在y2=x+a的图象的上方,即y1>y2,故③正确;
故选:B.
10.(2020春?西华县期末)函数y=|x﹣1|的图象是( )
A.
B.
C.
D.
【答案】B
【解答】解:∵函数y=|x﹣1|=,
∴当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小;
故选:B.
二.填空题(共8小题)
11.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是 2(答案不唯一) (写出一个答案即可).
【答案】2(答案不唯一).
【解答】解:∵一次函数y=(k﹣3)x+4,若y随x的增大而减小,
∴k﹣3<0,
解得k<3,
∴k可以取2.
故答案为:2(答案不唯一).
12.(2020春?营山县期末)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为 y=﹣2x+2 .
【答案】y=﹣2x+2.
【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵点A(﹣1,0)点B(0,﹣2)在直线AB上,
∴,
解得,
∴直线AB的解析式为y=﹣2x﹣2,
∵AB=AD,AO⊥BD,
∴OD=OB,
∴D(0,2),
∴直线CD的函数解析式为:y=﹣2x+2,
故答案为:y=﹣2x+2.
13.(2019秋?中原区校级期中)如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是 (﹣,) .
【答案】见试题解答内容
【解答】解:分别过点P、Q作x轴的垂线交于点M、N,
∵OP⊥OQ,∴∠POM+∠QON=90°,而∠QON+∠OQN=90°,
∴∠OQN=∠MOP,OP=OQ,∠PMO=∠ONQ=90°,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
设点P(m,﹣m+2),则点Q(﹣m+2,﹣m),
将点Q的坐标代入y=﹣得:﹣m=﹣(﹣m+2)+2,
解得:m=﹣,
故点P(﹣,),
故答案为:(﹣,).
14.(2020春?成华区期末)如图,在平面直角坐标系中,已知点A(4,0),B(0,5).将△BOA绕点A顺时针方向旋转得△B′O′A,若点B在B′O′的延长线上,则直线BB′的解析式为 y=﹣x+5. .
【答案】y=﹣x+5.
【解答】解:连接OO′交AB于M,
∵△BOA绕点A按顺时针方向旋转得△B′O′A,
∴△BOA≌△B′O′A,
∴AB=AB′,OA=AO′,
∵点B在B′O′的延长线上,AO′⊥BC,
∴BO′=B′O′=OB,
∵OA=AO′,BO=B′O′=BO′,
∴OO′⊥AB,
设直线AB解析式为y=kx+b,
把A与B坐标代入得:,
解得:,
∴直线AB解析式为y=﹣x+5,
∴直线OO′解析式为y=x,
联立得:,
解得:,即M(,),
∵M为线段OO′的中点,
∴O′(,),
设直线B′O′解析式为y=mx+n,
把B与O′坐标代入得:,
解得:m=﹣,n=4,
则直线CD解析式为y=﹣x+5.
故答案为:y=﹣x+5.
15.(2019秋?温州期末)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,与y轴交于点B,点P在线段AB上,PC⊥x轴于点C,则△PCO周长的最小值为 3+3 .
【答案】见试题解答内容
【解答】解:设点P(m,m+3),则PC=m+3,OC=﹣m,
△PCO周长=OP+OC+PC=OP+m+3﹣m+OP=3+PO,
即△PCO周长取得最小值时,只需要OP最小即可,
故点O作OD⊥AP,当点D、P重合时,OP(OD)最小,
△AOB为等腰直角三角形,则BOD也为等腰三角形,
设:OD=a,则DO=BD=a,
由勾股定理得:2a2=(3)2,解得:a=3=OD=OP,
故△PCO周长的最小值=3+PO=3+3,
故答案为:3+3.
16.(2020春?海淀区校级月考)如图,已知直线l1:y=﹣x+2与l2:y=x+,过直线????1与????轴的交点????1作????轴的垂线交????2于????1,过????1作????轴的平行线交????1于????2,再过????2作????轴的垂线交????2于????2,过????2作????轴的平行线????1交????3于,…,这样一直作下去,可在直线????1上继续得到点????4,????5,…,????????,….设点????????的横坐标为????????,则????????+1与????????的数量关系是 xn+2xn+1=3 .
【答案】xn+2xn+1=3.
【解答】解:令y=0,则﹣x+2=0,
解得x=2,
所以,P1(2,0),
∵P1Q1⊥x轴,
∴点Q1与P1的横坐标相同,
∴点Q1的纵坐标为×2+=,
∴点Q1的坐标为(2,),
∵P2Q1∥x轴,
∴点P2与Q1的纵横坐标相同,
∴﹣x+2=,
解得x=,
所以,点P2(,),
∵P2Q2⊥x轴,
∴点Q2与P2的横坐标相同,
∴点Q2的纵坐标为×+=,
∴点Q2的坐标为(,),
∵P3Q2∥x轴,
∴点P3与Q2的纵横坐标相同,
∴﹣x+2=,
解得x=,
所以,点P3(,),
…,
∵P1(2,0),P2(,),P3(,),
∴x2=,2+2×=3,+2×=3,
∴xn+2xn+1=3.
故答案为:xn+2xn+1=3.
17.(2020?唐山二模)如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是 29 ,第2019个阴影三角形的面积是 24037 .
【答案】见试题解答内容
【解答】解:当x=0时,y=x+2=2,
∴OA1=OB1=2;
当x=2时,y=x+2=4,
∴A2B1=B1B2=4;
当x=2+4=6时,y=x+2=8,
∴A3B2=B2B3=8;
当x=6+8=14时,y=x+2=16,
∴A4B3=B3B4=16.
∴An+1Bn=BnBn+1=2n+1,
∴Sn+1=×(2n+1)2=22n+1.
当n=4时,S5=22×4+1=29;当n=2018时,S2019=22×2018+1=24037.
故答案为:29,24037;
18.(2020春?定襄县期末)已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则A2020的坐标是 (22019﹣1,22019) .
【答案】(22019﹣1,22019).
【解答】解:∵直线y=x+1与y轴交于点A1,
∴A1的坐标为(0,1),则OA1=1,
∵四边形A1B1C1O是正方形,
∴OC1=OA1=1,
把x=1代入y=x+1得:y=2,
∴A2的坐标为(1,2),
同理A3的坐标为(3,4),…
∴An的坐标是(2n﹣1﹣1,2n﹣1),
∴A2020的坐标是(22019﹣1,22019).
故答案为:(22019﹣1,22019).
三.解答题(共9小题)
19.(2020春?庆安县期末)已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求这个一次函数的解析式;
(2)若点A(a,﹣2)在该函数的图象上,求a的值.
【答案】见试题解答内容
【解答】解:(1)设一次函数解析式为y=kx+b(k≠0),再把点(3,5)和(﹣4,﹣9)代入可得:,
解得:,
所以一次函数的解析式为:y=2x﹣1,
(2)把A(a,﹣2)在该函数的图象上,
可得:2a﹣1=﹣2,
解得:a=﹣0.5.
20.(2020春?孟津县期中)画出直线y=﹣2x+3的图象,根据图象解决下列问题:
(1)直线上找出横坐标是+2的点的坐标;
(2)写出y>0时,x的取值范围;
(3)写出直线上到x轴的距离等于4的点的坐标.
【答案】函数图象见解答;
(1)(2,﹣1);(2)x<1.5;(3)(﹣0.5,4)或(3.5,﹣4).
【解答】解:直线y=﹣2x+3过点(0,3)、(1.5,0),
函数图象如右图所示;
(1)当x=2时,y=﹣2×2+3=﹣1,
即直线上横坐标是+2的点的坐标是(2,﹣1);
(2)由图象可得,
y>0时,x的取值范围是x<1.5;
(3)当y=4时,4=﹣2x+3,解得,x=﹣0.5,
当y=﹣4时,﹣4=﹣2x+3,解得,x=3.5,
即直线上到x轴的距离等于4的点的坐标是(﹣0.5,4)或(3.5,﹣4).
21.(2020秋?渝中区校级月考)如图,已知一次函数y=x+3的图象分别与x轴、y轴交于点A、点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)若点P是x轴上的动点,且S△BOP=S△ABC,求符合条件的点P的坐标.
【答案】见试题解答内容
【解答】解:(1)当x=0时,y=x+3=3,
∴点B的坐标为(0,3);
当y=x+3=0时,x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C与点A关于y轴对称,
∴点C的坐标为(6,0),
设直线BC的函数解析式为y=kx+b,
∴,
∴,
∴直线BC的函数解析式为y=﹣x+3;
(2)设点P的坐标为(m,0),
∵S△BOP=S△ABC,
∴|m|×3=×12×3,
∴m=±3,
∴点P的坐标为(﹣3,0),(3,0).
22.(2020春?三台县期末)已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设△OBA的面积为S.
(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=12时B点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.
【答案】(1)S=40﹣4x(0<x<10);
(2)(7,3);
(3)(0,).
【解答】解:(1)∵x+y=10
∴y=10﹣x,
∴S=8(10﹣x)÷2=40﹣4x,
∵40﹣4x>0,
∴x<10,
∴0<x<10;
(2)∵s=12,
∴12=40﹣4x,
x=7
∴y=10﹣7=3,
∴S=12时,B点坐标(7,3);
(3)画出函数S的图形如图所示.
作出A的对称点A′,连接BA′,此时BA′与y轴交于点Q,此时BQ+AQ的值最小,
∵A点坐标为(8,0),
∴A′(﹣8,0),
∴将(﹣8,0),(7,3)代入y=kx+b,
∴,
解得:,
∴y=x+,
∴x=0时,y=,
当BQ+AQ的值最小时,Q点坐标为:(0,).
23.(2019秋?成华区期末)如图,一次函数y=kx+b的图象经过点A
(﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
【答案】见试题解答内容
【解答】解:(1)当x=1时,y=3x=3,
∴C(1,3),
将A
(﹣2,6),C(1,3)代入y=kx+b,得
,
解得,
∴直线AB的解析式是y=﹣x+4;
(2)y=﹣x+4中,令y=0,则x=4,
∴B(4,0),
设D(0,m)(m<0),
S△BOC=×OB×|yC|==6,
S△COD=×OD×|xC|=|m|×1=﹣m,
∵S△COD=S△BOC,
∴﹣m=,
解得m=﹣4,
∴D(0,﹣4).
24.(2019秋?新泰市期末)两个一次函数l1、l2的图象如图:
(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
【答案】见试题解答内容
【解答】解:(1)设直线L1的解析式是y=kx+b,已知L1经过点(0,﹣4),(2,0),
可得:,解得,
则函数的解析式是y=2x﹣4;
设直线L2的解析式是y=ax+n,已知L1经过点(0,2),(﹣4,0),
可得:,解得,
则函数的解析式是y=0.5x+2.
(2)联立两个方程可得:,
解得:,
所以点P坐标为(4,4),
S△APB=AB?|xP|=×6×4=12;
(3)∵P坐标为(4,4),
∴当x<4时,l1的图象在l2的下方.
25.(2019春?历城区期中)探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为 h1﹣h2=h .(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y=x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
【答案】见试题解答内容
【解答】解:(1)证明:如图①,连接AM,
①∵S△ABC=S△ABM+S△ACM,EM⊥AB,MF⊥AC,BD⊥AC,
∴AC?h=AB?h1+AC?h2,
又∵AB=AC,
∴h=h1+h2,
②如图③同理可得h1﹣h2=h,
故答案为:h1﹣h2=h;
(2)由题意可知,DE=DF=10,
∴△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,
∵h=EO=6,
∴M到DF(即x轴)的距离为6﹣2=4,
∴点M的纵坐标为4,此时可求得M,
当点M在射线FE上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离为8,
∴点M的纵坐标为9,此时可求得M,
故点M的坐标为或.
26.(2019秋?雨城区校级期中)如图,已知直线c和直线b相交于点(2,2),直线c过点(0,3).平行于y轴的动直线a的解析式为x=t,且动直线a分别交直线b、c于点D、E(E在D的上方).
(1)求直线b和直线c的解析式;
(2)若P是y轴上一个动点,且满足△PDE是等腰直角三角形,求点P的坐标.
【答案】见试题解答内容
【解答】解:(1)设直线b的解析式为:y=kx,
把(2,2)代入y=kx得,k=1,
∴直线b的解析式为:y=x;
设直线c的解析式为:y=kx+b,
把点(2,2),点(0,3)代入得,,
∴,
∴直线c的解析式为:y=﹣x+3;
(2)∵当x=t时,y=x=t;当x=t时,y=﹣x+3
=﹣t+3,
∴E点坐标为(t,﹣t+3),D点坐标为(t,t).
∵E在D的上方,
∴DE=﹣t+3﹣t
=﹣t+3,且t<2,
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
t>0时,PE=DE时,﹣t+3=t,
∴t=,﹣t+3=,
∴P点坐标为(0,),
①若t>0,PD=DE时,﹣t+3=t,
∴t=.∴P点坐标为(0,);
②若t>0,PE=PD时,即DE为斜边,∴﹣t+3=2t,
∴t=,DE的中点坐标为(t,t+),
∴P点坐标为(0,).
若t<0,PE=DE和PD=DE时,由已知得DE=﹣t,﹣t+3=﹣t,t=6>0
(不符合题意,舍去),
此时直线x=t不存在.
③若t<0,PE=PD时,即DE为斜边,由已知得DE=﹣2t,﹣t+3=﹣2t,
∴t=﹣6,t+=0,
∴P点坐标为(0,0)
综上所述:当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,)或(0,);
当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,);
当t=﹣6时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
27.(2018秋?九龙坡区校级期末)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点A(0,6),tan∠OBA=,直线OC与直线l1点相交于点C,且S△BOC=6.
(1)求直线l1的解析式和点C的坐标;
(2)点D是点B关于y轴的对称点,将直线OC沿y轴向下平移,记为直线l2,若直线l2经过点D,与直线l1交于点E,求△ADE的面积.
【答案】见试题解答内容
【解答】解:∵tan∠OBA=,且A(0,6),
∴OB=4,
∴B(4,0)
设AB解析式y=kx+b
∴,
解得:
∴直线I1的解析式:y=﹣x+6,
设C(a,﹣a+6),
∵S△BOC=6,
∴×4×[﹣(﹣a+6)]=6,
解得:a=2,
∴C(6,﹣3);
(2)∵点D是点B关于y轴的对称,
∴D(﹣4,0),
∵C(6,﹣3),
∴直线OC的解析式为:y=﹣x,
∵将直线OC沿y轴向下平移得到直线DE,
∴设直线DE的解析式为:y=﹣x+n,
把D(﹣4,0)代入得,0=﹣×(﹣4)+n,
∴n=﹣2,
∴直线DE的解析式为:y=﹣x﹣2,
∴直线DE与y轴的解得为(0,﹣2),
解得,
∴△ADE的面积=×4×(6+2)+×8×(6+2)=48.
声明:试题解析著作权属所有日期:2020/10/21
16:07:05;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
5.4一次函数的图像
一.选择题(共10小题)
1.(2020秋?九龙坡区校级月考)若一次函数y=kx+b的图象经过点(4,2)、(2,﹣2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.6
B.9
C.12
D.18
2.(2020春?南充期末)一次函数y=kx+b的图象如图所示,则下列说法:①kb>0;②若点A(﹣2,m)与B(3,n)都在直线y=kx+b上,则m>n;③当x>0时,y>b.其中正确的说法是( )
A.①②
B.①③
C.②③
D.①②③
3.(2020春?东坡区期末)在平面直角坐标系中,一次函数y=kx﹣3(k<0)的图象大致是( )
A.
B.
C.
D.
4.(2020?凉山州)若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是( )
A.m>﹣
B.m<3
C.﹣<m<3
D.﹣<m≤3
5.(2020春?丛台区校级期中)直线l:y=(m﹣3)x+n﹣2(m,n为常数)图象如图,化简|m﹣3|﹣的结果为( )
A.5﹣m﹣n
B.5
C.﹣1
D.m+n﹣5
6.(2020?邗江区校级一模)一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是( )
A.﹣3<x<0
B.x<0
C.﹣3<x<2
D.x>﹣3
7.(2020秋?鹿城区校级月考)如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8
B.5
C.6
D.8
8.(2020春?朝阳区校级月考)如图,在平面直角坐标系中,点A(2m,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.4
B.2
C.1
D.0
9.(2020春?迁西县期末)一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①a>0;②k>0;③当x<4时,kx+b>x+a,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
10.(2020春?西华县期末)函数y=|x﹣1|的图象是( )
A.
B.
C.
D.
二.填空题(共8小题)
11.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是
(写出一个答案即可).
12.(2020春?营山县期末)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为
.
13.(2019秋?中原区校级期中)如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是
.
14.(2020春?成华区期末)如图,在平面直角坐标系中,已知点A(4,0),B(0,5).将△BOA绕点A顺时针方向旋转得△B′O′A,若点B在B′O′的延长线上,则直线BB′的解析式为
.
15.(2019秋?温州期末)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,与y轴交于点B,点P在线段AB上,PC⊥x轴于点C,则△PCO周长的最小值为
.
16.(2020春?海淀区校级月考)如图,已知直线l1:y=﹣x+2与l2:y=x+,过直线????1与????轴的交点????1作????轴的垂线交????2于????1,过????1作????轴的平行线交????1于????2,再过????2作????轴的垂线交????2于????2,过????2作????轴的平行线????1交????3于,…,这样一直作下去,可在直线????1上继续得到点????4,????5,…,????????,….设点????????的横坐标为????????,则????????+1与????????的数量关系是
.
17.(2020?唐山二模)如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是
,第2019个阴影三角形的面积是
.
18.(2020春?定襄县期末)已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则A2020的坐标是
.
三.解答题(共9小题)
19.(2020春?庆安县期末)已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求这个一次函数的解析式;
(2)若点A(a,﹣2)在该函数的图象上,求a的值.
20.(2020春?孟津县期中)画出直线y=﹣2x+3的图象,根据图象解决下列问题:
(1)直线上找出横坐标是+2的点的坐标;
(2)写出y>0时,x的取值范围;
(3)写出直线上到x轴的距离等于4的点的坐标.
21.(2020秋?渝中区校级月考)如图,已知一次函数y=x+3的图象分别与x轴、y轴交于点A、点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)若点P是x轴上的动点,且S△BOP=S△ABC,求符合条件的点P的坐标.
22.(2020春?三台县期末)已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设△OBA的面积为S.
(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=12时B点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.
23.(2019秋?成华区期末)如图,一次函数y=kx+b的图象经过点A
(﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
24.(2019秋?新泰市期末)两个一次函数l1、l2的图象如图:
(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
25.(2019春?历城区期中)探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为
.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y=x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
26.(2019秋?雨城区校级期中)如图,已知直线c和直线b相交于点(2,2),直线c过点(0,3).平行于y轴的动直线a的解析式为x=t,且动直线a分别交直线b、c于点D、E(E在D的上方).
(1)求直线b和直线c的解析式;
(2)若P是y轴上一个动点,且满足△PDE是等腰直角三角形,求点P的坐标.
27.(2018秋?九龙坡区校级期末)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点A(0,6),tan∠OBA=,直线OC与直线l1点相交于点C,且S△BOC=6.
(1)求直线l1的解析式和点C的坐标;
(2)点D是点B关于y轴的对称点,将直线OC沿y轴向下平移,记为直线l2,若直线l2经过点D,与直线l1交于点E,求△ADE的面积.
5.4一次函数的图像
参考答案与试题解析
一.选择题(共10小题)
1.(2020秋?九龙坡区校级月考)若一次函数y=kx+b的图象经过点(4,2)、(2,﹣2),则该一次函数图象与两坐标轴围成的三角形的面积为( )
A.6
B.9
C.12
D.18
【答案】B
【解答】解:将(4,2),(2,﹣2)代入y=kx+b,得:,
解得:,
∴一次函数的解析式为y=2x﹣6.
当x=0时,y=2×0﹣6=﹣6,
∴一次函数y=2x﹣6与y轴的交点坐标为(0,﹣6);
当y=0时,2x﹣6=0,解得:x=3,
∴一次函数y=2x﹣6与x轴的交点坐标为(3,0).
∴一次函数y=2x﹣6与两坐标轴围成的三角形的面积=×6×3=9.
故选:B.
2.(2020春?南充期末)一次函数y=kx+b的图象如图所示,则下列说法:①kb>0;②若点A(﹣2,m)与B(3,n)都在直线y=kx+b上,则m>n;③当x>0时,y>b.其中正确的说法是( )
A.①②
B.①③
C.②③
D.①②③
【答案】B
【解答】解:①∵图象过第一,第二,第三象限,
∴k>0,b>0,
∴kb>0正确,符合题意;
②由①知,y随x增大而增大,
∵﹣2<3,故m<n,
故②错误,不符合题意;
③当x=0时,y=kx+b=b,
∴当x>0时,从图象看,y>b正确,符合题意;
故选:B.
3.(2020春?东坡区期末)在平面直角坐标系中,一次函数y=kx﹣3(k<0)的图象大致是( )
A.
B.
C.
D.
【答案】C
【解答】解:∵一次函数y=kx﹣3(k<0),b=﹣3,
∴该函数图象经过第二、三、四象限,
故选:C.
4.(2020?凉山州)若一次函数y=(2m+1)x+m﹣3的图象不经过第二象限,则m的取值范围是( )
A.m>﹣
B.m<3
C.﹣<m<3
D.﹣<m≤3
【答案】D
【解答】解:根据题意得,
解得﹣<m≤3.
故选:D.
5.(2020春?丛台区校级期中)直线l:y=(m﹣3)x+n﹣2(m,n为常数)图象如图,化简|m﹣3|﹣的结果为( )
A.5﹣m﹣n
B.5
C.﹣1
D.m+n﹣5
【答案】A
【解答】解:∵直线l:y=(m﹣3)x﹣2+n(m,n为常数)的图象过第一、二、四象限,
∴m﹣3<0,n﹣2>0,
∴|m﹣3|﹣
=3﹣m﹣|n﹣2|
=3﹣m﹣(n﹣2)
=3﹣m﹣n+2
=5﹣m﹣n.
故选:A.
6.(2020?邗江区校级一模)一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是( )
A.﹣3<x<0
B.x<0
C.﹣3<x<2
D.x>﹣3
【答案】A
【解答】解:函数图象如图所示,函数图象在第二象限时,自变量x的取值范围是﹣3<x<0.
故选:A.
7.(2020秋?鹿城区校级月考)如图,直线y=﹣x+6与x轴,y轴分别交于点A和点B,点M是线段AB的中点,则线段OM的长为( )
A.4.8
B.5
C.6
D.8
【答案】B
【解答】解:把x=0代入y=﹣x+6得:
y=6,
即点B的坐标为(0,6),
把y=0代入y=﹣x+6得:
﹣x+6=0,
解得:x=8,
即点A的坐标为(8,0),
∴AB==10,
∵点M是线段AB的中点,
∴OM=AB=5,
故选:B.
8.(2020春?朝阳区校级月考)如图,在平面直角坐标系中,点A(2m,m)在第一象限,若点A关于x轴的对称点B在直线y=﹣x+1上,则m的值为( )
A.4
B.2
C.1
D.0
【答案】C
【解答】解:∵点A(2m,m)在第一象限,若点A关于x轴的对称点为点B,
∴B(2m,﹣m),
∵点B在直线y=﹣x+1上,
∴﹣m=﹣2m+1,
∴m=1,
故选:C.
9.(2020春?迁西县期末)一次函数y1=kx+b与y2=x+a的图象如图所示,有下列结论:①a>0;②k>0;③当x<4时,kx+b>x+a,其中正确的结论有( )
A.0个
B.1个
C.2个
D.3个
【答案】B
【解答】解:①∵y2=x+a的图象与y轴的交点在负半轴上,
∴a<0,
故①错误;
②∵y1=kx+b的图象从左向右呈下降趋势,
∴k<0,故②错误;
③两函数图象的交点横坐标为4,
当x<4时,y1=kx+b在y2=x+a的图象的上方,即y1>y2,故③正确;
故选:B.
10.(2020春?西华县期末)函数y=|x﹣1|的图象是( )
A.
B.
C.
D.
【答案】B
【解答】解:∵函数y=|x﹣1|=,
∴当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小;
故选:B.
二.填空题(共8小题)
11.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是 2(答案不唯一) (写出一个答案即可).
【答案】2(答案不唯一).
【解答】解:∵一次函数y=(k﹣3)x+4,若y随x的增大而减小,
∴k﹣3<0,
解得k<3,
∴k可以取2.
故答案为:2(答案不唯一).
12.(2020春?营山县期末)如图,已知一条直线经过点A(﹣1,0),B(0,﹣2),将这条直线向右平移与x轴、y轴分别交于点C、D,若AB=AD,则直线CD的函数表达式为 y=﹣2x+2 .
【答案】y=﹣2x+2.
【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵点A(﹣1,0)点B(0,﹣2)在直线AB上,
∴,
解得,
∴直线AB的解析式为y=﹣2x﹣2,
∵AB=AD,AO⊥BD,
∴OD=OB,
∴D(0,2),
∴直线CD的函数解析式为:y=﹣2x+2,
故答案为:y=﹣2x+2.
13.(2019秋?中原区校级期中)如图,点P,Q是直线y=﹣上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是 (﹣,) .
【答案】见试题解答内容
【解答】解:分别过点P、Q作x轴的垂线交于点M、N,
∵OP⊥OQ,∴∠POM+∠QON=90°,而∠QON+∠OQN=90°,
∴∠OQN=∠MOP,OP=OQ,∠PMO=∠ONQ=90°,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
设点P(m,﹣m+2),则点Q(﹣m+2,﹣m),
将点Q的坐标代入y=﹣得:﹣m=﹣(﹣m+2)+2,
解得:m=﹣,
故点P(﹣,),
故答案为:(﹣,).
14.(2020春?成华区期末)如图,在平面直角坐标系中,已知点A(4,0),B(0,5).将△BOA绕点A顺时针方向旋转得△B′O′A,若点B在B′O′的延长线上,则直线BB′的解析式为 y=﹣x+5. .
【答案】y=﹣x+5.
【解答】解:连接OO′交AB于M,
∵△BOA绕点A按顺时针方向旋转得△B′O′A,
∴△BOA≌△B′O′A,
∴AB=AB′,OA=AO′,
∵点B在B′O′的延长线上,AO′⊥BC,
∴BO′=B′O′=OB,
∵OA=AO′,BO=B′O′=BO′,
∴OO′⊥AB,
设直线AB解析式为y=kx+b,
把A与B坐标代入得:,
解得:,
∴直线AB解析式为y=﹣x+5,
∴直线OO′解析式为y=x,
联立得:,
解得:,即M(,),
∵M为线段OO′的中点,
∴O′(,),
设直线B′O′解析式为y=mx+n,
把B与O′坐标代入得:,
解得:m=﹣,n=4,
则直线CD解析式为y=﹣x+5.
故答案为:y=﹣x+5.
15.(2019秋?温州期末)如图,在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,与y轴交于点B,点P在线段AB上,PC⊥x轴于点C,则△PCO周长的最小值为 3+3 .
【答案】见试题解答内容
【解答】解:设点P(m,m+3),则PC=m+3,OC=﹣m,
△PCO周长=OP+OC+PC=OP+m+3﹣m+OP=3+PO,
即△PCO周长取得最小值时,只需要OP最小即可,
故点O作OD⊥AP,当点D、P重合时,OP(OD)最小,
△AOB为等腰直角三角形,则BOD也为等腰三角形,
设:OD=a,则DO=BD=a,
由勾股定理得:2a2=(3)2,解得:a=3=OD=OP,
故△PCO周长的最小值=3+PO=3+3,
故答案为:3+3.
16.(2020春?海淀区校级月考)如图,已知直线l1:y=﹣x+2与l2:y=x+,过直线????1与????轴的交点????1作????轴的垂线交????2于????1,过????1作????轴的平行线交????1于????2,再过????2作????轴的垂线交????2于????2,过????2作????轴的平行线????1交????3于,…,这样一直作下去,可在直线????1上继续得到点????4,????5,…,????????,….设点????????的横坐标为????????,则????????+1与????????的数量关系是 xn+2xn+1=3 .
【答案】xn+2xn+1=3.
【解答】解:令y=0,则﹣x+2=0,
解得x=2,
所以,P1(2,0),
∵P1Q1⊥x轴,
∴点Q1与P1的横坐标相同,
∴点Q1的纵坐标为×2+=,
∴点Q1的坐标为(2,),
∵P2Q1∥x轴,
∴点P2与Q1的纵横坐标相同,
∴﹣x+2=,
解得x=,
所以,点P2(,),
∵P2Q2⊥x轴,
∴点Q2与P2的横坐标相同,
∴点Q2的纵坐标为×+=,
∴点Q2的坐标为(,),
∵P3Q2∥x轴,
∴点P3与Q2的纵横坐标相同,
∴﹣x+2=,
解得x=,
所以,点P3(,),
…,
∵P1(2,0),P2(,),P3(,),
∴x2=,2+2×=3,+2×=3,
∴xn+2xn+1=3.
故答案为:xn+2xn+1=3.
17.(2020?唐山二模)如图,在平面直角坐标系中,直线y=x+2交x轴于点A,交y轴于点A1,若图中阴影部分的三角形都是等腰直角三角形,则从左往右数第5个阴影三角形的面积是 29 ,第2019个阴影三角形的面积是 24037 .
【答案】见试题解答内容
【解答】解:当x=0时,y=x+2=2,
∴OA1=OB1=2;
当x=2时,y=x+2=4,
∴A2B1=B1B2=4;
当x=2+4=6时,y=x+2=8,
∴A3B2=B2B3=8;
当x=6+8=14时,y=x+2=16,
∴A4B3=B3B4=16.
∴An+1Bn=BnBn+1=2n+1,
∴Sn+1=×(2n+1)2=22n+1.
当n=4时,S5=22×4+1=29;当n=2018时,S2019=22×2018+1=24037.
故答案为:29,24037;
18.(2020春?定襄县期末)已知正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1,A2,A3…在直线y=x+1上,C1,C2,C3…在x轴上,则A2020的坐标是 (22019﹣1,22019) .
【答案】(22019﹣1,22019).
【解答】解:∵直线y=x+1与y轴交于点A1,
∴A1的坐标为(0,1),则OA1=1,
∵四边形A1B1C1O是正方形,
∴OC1=OA1=1,
把x=1代入y=x+1得:y=2,
∴A2的坐标为(1,2),
同理A3的坐标为(3,4),…
∴An的坐标是(2n﹣1﹣1,2n﹣1),
∴A2020的坐标是(22019﹣1,22019).
故答案为:(22019﹣1,22019).
三.解答题(共9小题)
19.(2020春?庆安县期末)已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求这个一次函数的解析式;
(2)若点A(a,﹣2)在该函数的图象上,求a的值.
【答案】见试题解答内容
【解答】解:(1)设一次函数解析式为y=kx+b(k≠0),再把点(3,5)和(﹣4,﹣9)代入可得:,
解得:,
所以一次函数的解析式为:y=2x﹣1,
(2)把A(a,﹣2)在该函数的图象上,
可得:2a﹣1=﹣2,
解得:a=﹣0.5.
20.(2020春?孟津县期中)画出直线y=﹣2x+3的图象,根据图象解决下列问题:
(1)直线上找出横坐标是+2的点的坐标;
(2)写出y>0时,x的取值范围;
(3)写出直线上到x轴的距离等于4的点的坐标.
【答案】函数图象见解答;
(1)(2,﹣1);(2)x<1.5;(3)(﹣0.5,4)或(3.5,﹣4).
【解答】解:直线y=﹣2x+3过点(0,3)、(1.5,0),
函数图象如右图所示;
(1)当x=2时,y=﹣2×2+3=﹣1,
即直线上横坐标是+2的点的坐标是(2,﹣1);
(2)由图象可得,
y>0时,x的取值范围是x<1.5;
(3)当y=4时,4=﹣2x+3,解得,x=﹣0.5,
当y=﹣4时,﹣4=﹣2x+3,解得,x=3.5,
即直线上到x轴的距离等于4的点的坐标是(﹣0.5,4)或(3.5,﹣4).
21.(2020秋?渝中区校级月考)如图,已知一次函数y=x+3的图象分别与x轴、y轴交于点A、点B,点C与点A关于y轴对称.
(1)求直线BC的函数解析式;
(2)若点P是x轴上的动点,且S△BOP=S△ABC,求符合条件的点P的坐标.
【答案】见试题解答内容
【解答】解:(1)当x=0时,y=x+3=3,
∴点B的坐标为(0,3);
当y=x+3=0时,x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C与点A关于y轴对称,
∴点C的坐标为(6,0),
设直线BC的函数解析式为y=kx+b,
∴,
∴,
∴直线BC的函数解析式为y=﹣x+3;
(2)设点P的坐标为(m,0),
∵S△BOP=S△ABC,
∴|m|×3=×12×3,
∴m=±3,
∴点P的坐标为(﹣3,0),(3,0).
22.(2020春?三台县期末)已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设△OBA的面积为S.
(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=12时B点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.
【答案】(1)S=40﹣4x(0<x<10);
(2)(7,3);
(3)(0,).
【解答】解:(1)∵x+y=10
∴y=10﹣x,
∴S=8(10﹣x)÷2=40﹣4x,
∵40﹣4x>0,
∴x<10,
∴0<x<10;
(2)∵s=12,
∴12=40﹣4x,
x=7
∴y=10﹣7=3,
∴S=12时,B点坐标(7,3);
(3)画出函数S的图形如图所示.
作出A的对称点A′,连接BA′,此时BA′与y轴交于点Q,此时BQ+AQ的值最小,
∵A点坐标为(8,0),
∴A′(﹣8,0),
∴将(﹣8,0),(7,3)代入y=kx+b,
∴,
解得:,
∴y=x+,
∴x=0时,y=,
当BQ+AQ的值最小时,Q点坐标为:(0,).
23.(2019秋?成华区期末)如图,一次函数y=kx+b的图象经过点A
(﹣2,6),与x轴交于点B,与正比例函数y=3x的图象交于点C,点C的横坐标为1.
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足S△COD=S△BOC,求点D的坐标.
【答案】见试题解答内容
【解答】解:(1)当x=1时,y=3x=3,
∴C(1,3),
将A
(﹣2,6),C(1,3)代入y=kx+b,得
,
解得,
∴直线AB的解析式是y=﹣x+4;
(2)y=﹣x+4中,令y=0,则x=4,
∴B(4,0),
设D(0,m)(m<0),
S△BOC=×OB×|yC|==6,
S△COD=×OD×|xC|=|m|×1=﹣m,
∵S△COD=S△BOC,
∴﹣m=,
解得m=﹣4,
∴D(0,﹣4).
24.(2019秋?新泰市期末)两个一次函数l1、l2的图象如图:
(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
【答案】见试题解答内容
【解答】解:(1)设直线L1的解析式是y=kx+b,已知L1经过点(0,﹣4),(2,0),
可得:,解得,
则函数的解析式是y=2x﹣4;
设直线L2的解析式是y=ax+n,已知L1经过点(0,2),(﹣4,0),
可得:,解得,
则函数的解析式是y=0.5x+2.
(2)联立两个方程可得:,
解得:,
所以点P坐标为(4,4),
S△APB=AB?|xP|=×6×4=12;
(3)∵P坐标为(4,4),
∴当x<4时,l1的图象在l2的下方.
25.(2019春?历城区期中)探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰△ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为 h1﹣h2=h .(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y=x+6;l2:y=﹣3x+6.若l2上的一点M到l1的距离是2,请你利用以上结论求解点M的坐标.
【答案】见试题解答内容
【解答】解:(1)证明:如图①,连接AM,
①∵S△ABC=S△ABM+S△ACM,EM⊥AB,MF⊥AC,BD⊥AC,
∴AC?h=AB?h1+AC?h2,
又∵AB=AC,
∴h=h1+h2,
②如图③同理可得h1﹣h2=h,
故答案为:h1﹣h2=h;
(2)由题意可知,DE=DF=10,
∴△EDF是等腰三角形,
当点M在线段EF上时,依据(1)中结论,
∵h=EO=6,
∴M到DF(即x轴)的距离为6﹣2=4,
∴点M的纵坐标为4,此时可求得M,
当点M在射线FE上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离为8,
∴点M的纵坐标为9,此时可求得M,
故点M的坐标为或.
26.(2019秋?雨城区校级期中)如图,已知直线c和直线b相交于点(2,2),直线c过点(0,3).平行于y轴的动直线a的解析式为x=t,且动直线a分别交直线b、c于点D、E(E在D的上方).
(1)求直线b和直线c的解析式;
(2)若P是y轴上一个动点,且满足△PDE是等腰直角三角形,求点P的坐标.
【答案】见试题解答内容
【解答】解:(1)设直线b的解析式为:y=kx,
把(2,2)代入y=kx得,k=1,
∴直线b的解析式为:y=x;
设直线c的解析式为:y=kx+b,
把点(2,2),点(0,3)代入得,,
∴,
∴直线c的解析式为:y=﹣x+3;
(2)∵当x=t时,y=x=t;当x=t时,y=﹣x+3
=﹣t+3,
∴E点坐标为(t,﹣t+3),D点坐标为(t,t).
∵E在D的上方,
∴DE=﹣t+3﹣t
=﹣t+3,且t<2,
∵△PDE为等腰直角三角形,∴PE=DE或PD=DE或PE=PD.
t>0时,PE=DE时,﹣t+3=t,
∴t=,﹣t+3=,
∴P点坐标为(0,),
①若t>0,PD=DE时,﹣t+3=t,
∴t=.∴P点坐标为(0,);
②若t>0,PE=PD时,即DE为斜边,∴﹣t+3=2t,
∴t=,DE的中点坐标为(t,t+),
∴P点坐标为(0,).
若t<0,PE=DE和PD=DE时,由已知得DE=﹣t,﹣t+3=﹣t,t=6>0
(不符合题意,舍去),
此时直线x=t不存在.
③若t<0,PE=PD时,即DE为斜边,由已知得DE=﹣2t,﹣t+3=﹣2t,
∴t=﹣6,t+=0,
∴P点坐标为(0,0)
综上所述:当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,)或(0,);
当t=时,△PDE为等腰直角三角形,此时P点坐标为(0,);
当t=﹣6时,△PDE为等腰直角三角形,此时P点坐标为(0,0).
27.(2018秋?九龙坡区校级期末)如图,在平面直角坐标系中,直线l1与x轴交于点B,与y轴交于点A(0,6),tan∠OBA=,直线OC与直线l1点相交于点C,且S△BOC=6.
(1)求直线l1的解析式和点C的坐标;
(2)点D是点B关于y轴的对称点,将直线OC沿y轴向下平移,记为直线l2,若直线l2经过点D,与直线l1交于点E,求△ADE的面积.
【答案】见试题解答内容
【解答】解:∵tan∠OBA=,且A(0,6),
∴OB=4,
∴B(4,0)
设AB解析式y=kx+b
∴,
解得:
∴直线I1的解析式:y=﹣x+6,
设C(a,﹣a+6),
∵S△BOC=6,
∴×4×[﹣(﹣a+6)]=6,
解得:a=2,
∴C(6,﹣3);
(2)∵点D是点B关于y轴的对称,
∴D(﹣4,0),
∵C(6,﹣3),
∴直线OC的解析式为:y=﹣x,
∵将直线OC沿y轴向下平移得到直线DE,
∴设直线DE的解析式为:y=﹣x+n,
把D(﹣4,0)代入得,0=﹣×(﹣4)+n,
∴n=﹣2,
∴直线DE的解析式为:y=﹣x﹣2,
∴直线DE与y轴的解得为(0,﹣2),
解得,
∴△ADE的面积=×4×(6+2)+×8×(6+2)=48.
声明:试题解析著作权属所有日期:2020/10/21
16:07:05;用户:1032650243;邮箱:1032650243@qq.com;学号:20715072
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
