特殊三角形复习学案

特殊三角形专题复习之----折叠中的直角三角形（学案）
学校 班级 姓名
巧设情境，设疑引入
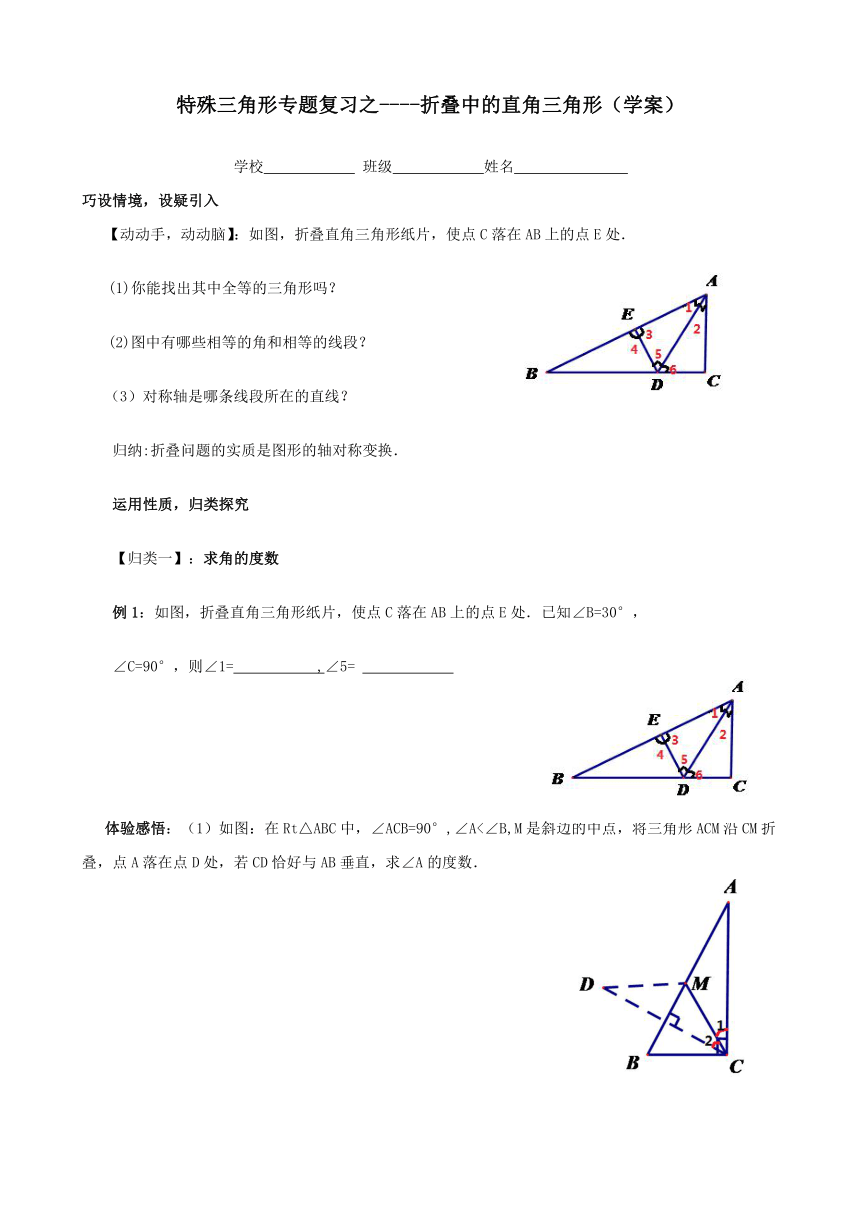
【动动手，动动脑】：如图，折叠直角三角形纸片，使点C落在AB上的点E处．
(1)你能找出其中全等的三角形吗？
(2)图中有哪些相等的角和相等的线段？
（3）对称轴是哪条线段所在的直线？
归纳:折叠问题的实质是图形的轴对称变换．
运用性质，归类探究
【归类一】：求角的度数
例1：如图，折叠直角三角形纸片，使点C落在AB上的点E处．已知∠B=30°，
∠C=90°，则∠1= ,∠5=
体验感悟：（1）如图：在Rt△ABC中，∠ACB=90°,∠A<∠B,M是斜边的中点，将三角形ACM沿CM折叠，点A落在点D处，若CD恰好与AB垂直，求∠A的度数．
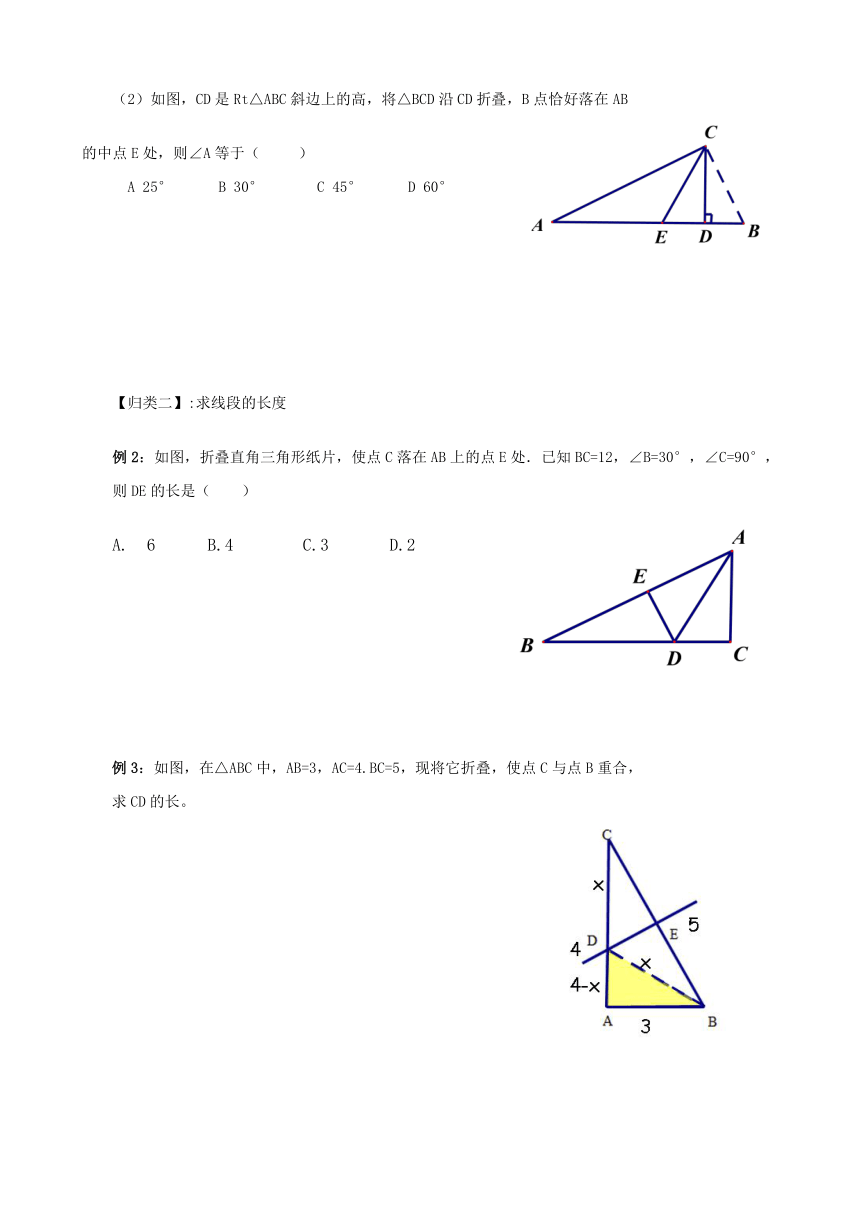
（2）如图，CD是Rt△ABC斜边上的高，将△BCD沿CD折叠，B点恰好落在AB
的中点E处，则∠A等于（ ）
A 25° B 30° C 45° D 60°
【归类二】:求线段的长度
例2：如图，折叠直角三角形纸片，使点C落在AB上的点E处．已知BC=12，∠B=30°，∠C=90°，则DE的长是（　　）
A. 6 B.4 C.3 D.2
例3：如图，在△ABC中，AB=3，AC=4.BC=5，现将它折叠，使点C与点B重合，
求CD的长。
体验感悟：如图，把一张长 8,宽 4的长方形纸片折叠,折叠后使相对的两个点A、C重合,点D落
在D′，折痕为EF,求:重合部分的面积.
【归类三】：综合运用
（09黑龙江中考）如图，将长方形纸片ABCD沿直线AC折叠，使点B落到点B′的位置，AB′与CD交于点E.
（1）试找出一个与△AED全等的三角形，并加以证明.
（2）若AB=8，DE=3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，试求PG+PH的值，并说明理由.
课外拓展：
(1)如图，将等腰直角三角形按图示方式翻折，若DE=2，下列说法正确的个数有（　　）
①△BC′D是等腰三角形；②△CED的周长等于BC的长；③DC′平分∠BDE；④BE长为2+4．
A.1个 B.2个 C.3个 D.4个