3[1].1直线与圆的位置关系

(共14张PPT)
地平线
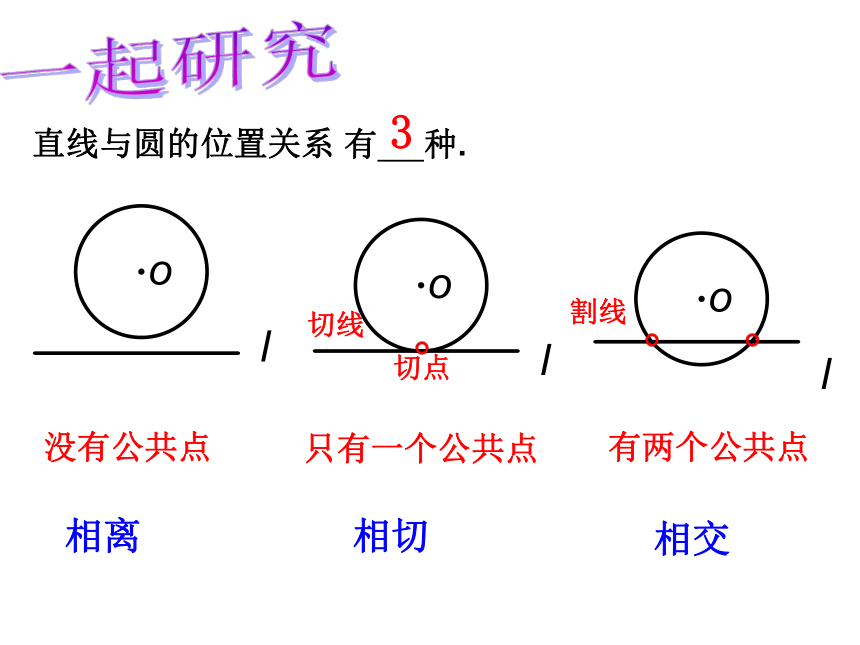
直线与圆的位置关系
3
没有公共点
相离
只有一个公共点
相切
切点
切线
有两个公共点
相交
割线
有 种.
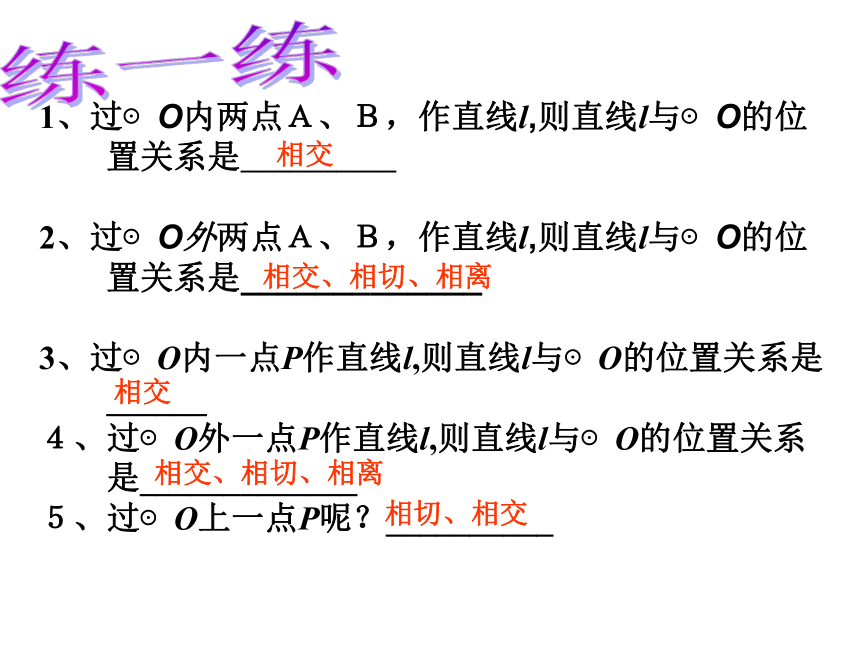
1、过⊙O内两点Ａ、Ｂ，作直线l,则直线l与⊙O的位　　　　　　　　　　　　
　　置关系是_____________
2、过⊙O外两点Ａ、Ｂ，作直线l,则直线l与⊙O的位　　　　　　　　　　　　
　　置关系是_____________
3、过⊙O内一点P作直线l,则直线l与⊙O的位置关系是　
　　______
４、过⊙O外一点P作直线l,则直线l与⊙O的位置关系　　　
　　是_____________
５、过⊙O上一点P呢？__________
相交
相交、相切、相离
相切、相交
相交
相交、相切、相离
已知直线l外一点O到直线L的距离为d,d=3cm.请你以O为圆心
1)R=2cm做一个圆,则直线和圆位置是什么关系
2) R=4cm做一个圆,则直线和圆位置是什么关系
3)猜想他的半径是多少的时候这个圆和直线相切
请用圆规验证你的猜想.
O
L
T
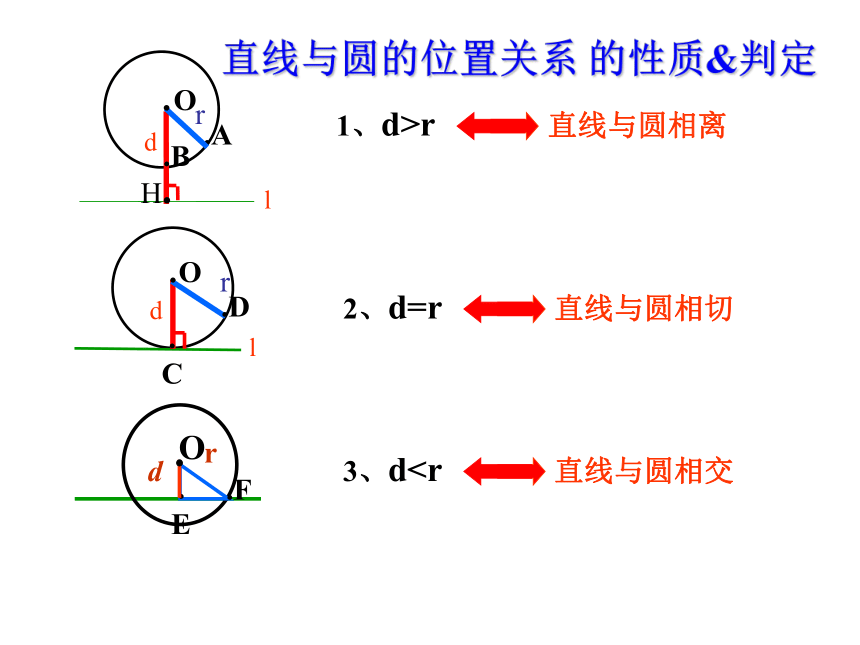
直线与圆的位置关系 的性质&判定
d
r
l
.D
.
C
.O
d
r
.A
l
H.
.O
.B
r
d
.
E
.F
O
1、d>r 直线与圆相离
2、d=r 直线与圆相切
3、d设⊙O的半径为r，圆心O到直线l的距离为d。根据下列条件判断直线l与⊙O的位置关系。
（2）d=1,r= ；
（3）d=2,r=2；
（1）d=4,r=3；
∵ d ＜ r
∴直线l与⊙O相交
∵d＝r
∴直线l与⊙O相切
∵d＞ r
∴直线l与⊙O相离
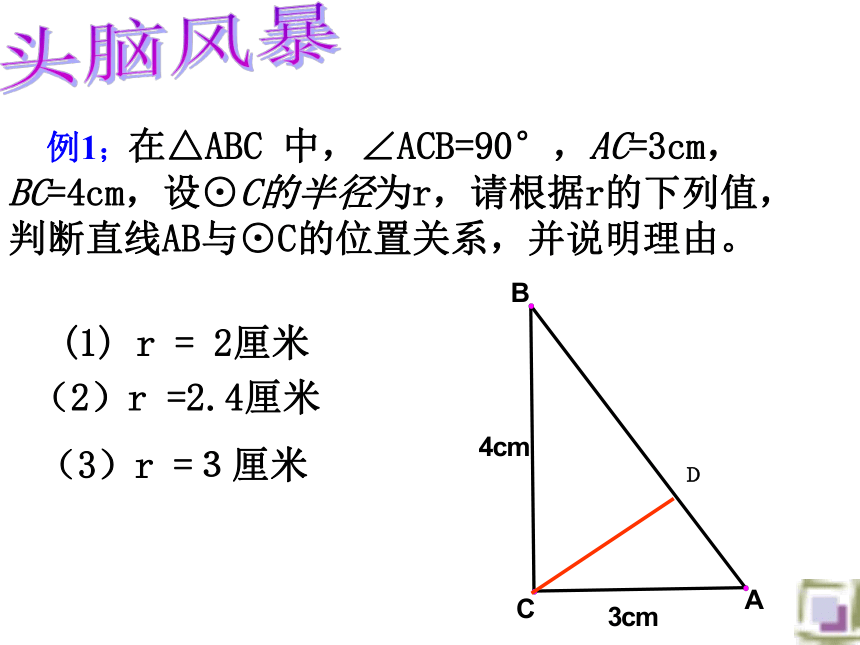
例1；在△ABC 中，∠ACB=90°，AC=3cm，BC=4cm，设⊙C的半径为r，请根据r的下列值，判断直线AB与⊙C的位置关系，并说明理由。
(1) r = 2厘米
（2）r =2.4厘米
（3）r =３厘米
Ｄ
A
B
C
D
3cm
4cm
(1) r = 2
（2）r =2.4
A
B
C
D
3cm
4cm
（３）r =３
A
B
C
D
3cm
4cm
当r =2cm时，
d > r，
∴☉C 与
直线AB相离；
当r =2.4cm时，
d = r，
∴☉C 与直线AB相切；
当r =3cm时，
d < r，
∴☉C 与直线AB相交。
2.4cm
2.4cm
2.4cm
在△ABC 中，∠ACB=90°，
AC=3cm，BC=4cm，设⊙C的半径为r。
1、当r满足___________时，⊙C与直线AB相离．
2、当r满足__________ 时,⊙C与直线AB相切．
0r=2.4cm
A
B
C
D
3cm
4cm
2.4cm
3、当r满足____________时,⊙C与直线AB相交．
r＞2.4cm
O
北
A
C
O1
C1
2)台风沿OA方向以每小时20公里的速 度正面袭击A城市.几点钟开始公路必 须停止运营？
Ｌ
例2、我省的气象台上午6点测得一台风中心位于A市南偏东30 方向280公里的海面上 ，预计他的周围100公里范围要受到台风影响。如图有一公路Ｌ经过A城市横穿南北。问：
1）此时该公路有没有受到台风　　
　　的影响
3)受台风影响雷达出故障，只测得台风中心位于A市南偏东30 方向,A市正南方向的B市测得台风中心位于B市东南方 ，预计他的周围100公里范围要受到影响。如图有一公路Ｌ经过A、B两市,已知AB两城市距离100公里.
O
北
A
B
此时该公路有没有受到台风的影响
C
北
L
A
B
C
O
Ｌ
相离
相切
相交
两个
一个
没有
切点
切线
割线
d>r
d=r
d判定直线与圆的位置关系的方法有____种：
（1）由________________ 的个数来判断；
（2）由_______________________
的数量大小关系来判断．
注意：在实际应用中，常采用第二种方法判定．
两
直线与圆的公共点
圆心到直线的距离d与半径r