相似三角形综合复习（1）

(共16张PPT)
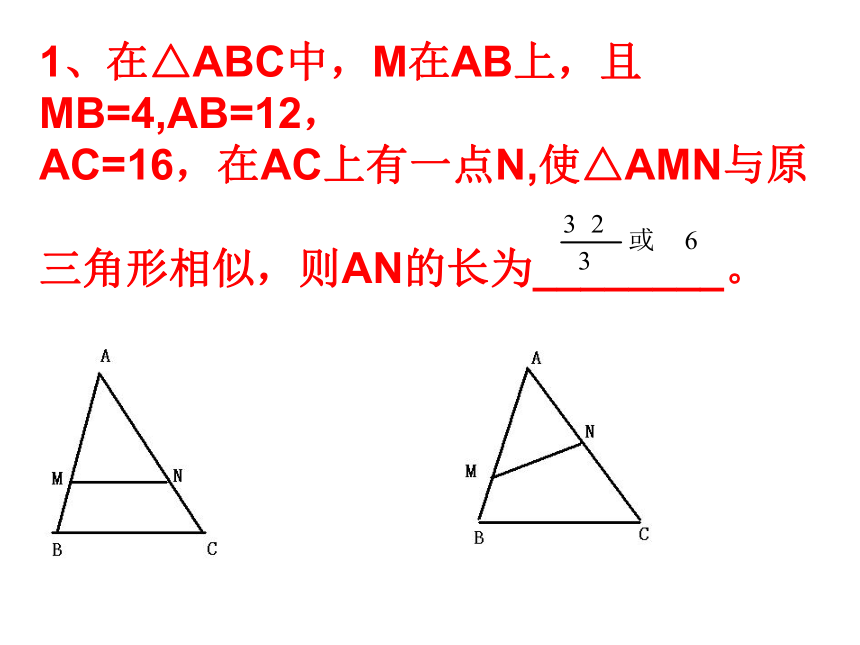
1、在△ABC中，M在AB上，且MB=4,AB=12，
AC=16，在AC上有一点N,使△AMN与原
三角形相似，则AN的长为________。
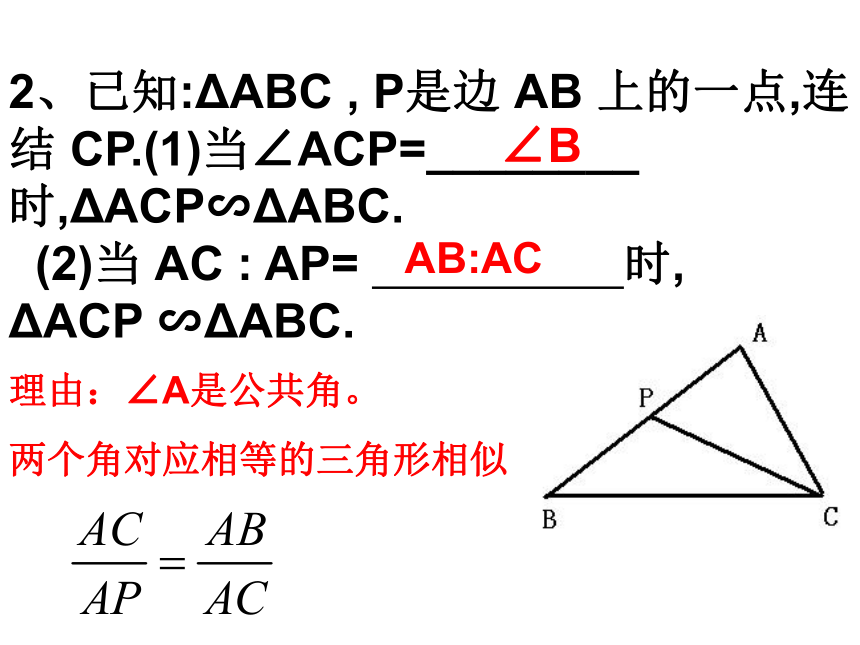
2、已知:ΔABC , P是边 AB 上的一点,连结 CP.(1)当∠ACP=________时,ΔACP∽ΔABC.
(2)当 AC : AP= 时,
ΔACP ∽ΔABC.
∠B
AB:AC
理由：∠A是公共角。
两个角对应相等的三角形相似
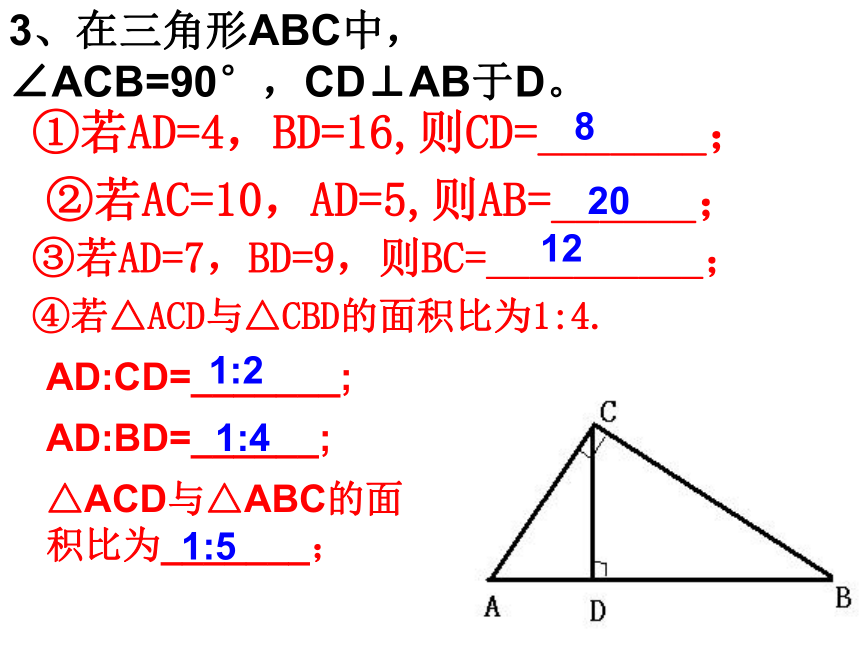
3、在三角形ABC中，∠ACB=90°，CD⊥AB于D。
①若AD=4，BD=16,则CD=_______；
②若AC=10，AD=5,则AB=______；
④若△ACD与△CBD的面积比为1:4.
③若AD=7，BD=9，则BC=__________；
AD:CD=_______;
AD:BD=______;
△ACD与△ABC的面积比为_______；
20
8
12
1:2
1:4
1:5
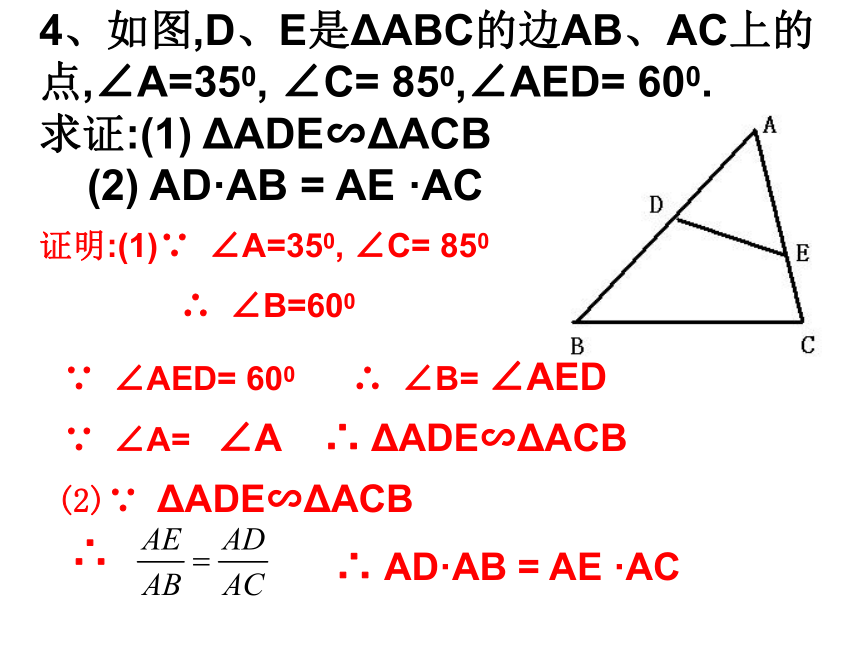
4、如图,D、E是ΔABC的边AB、AC上的点,∠A=350, ∠C= 850,∠AED= 600.
求证:(1) ΔADE∽ΔACB
(2) AD·AB = AE ·AC
证明:(1)∵ ∠A=350, ∠C= 850
∴ ∠B=600
∵ ∠AED= 600 ∴ ∠B= ∠AED
∵ ∠A= ∠A ∴ ΔADE∽ΔACB
(2)∵ ΔADE∽ΔACB
∴
∴ AD·AB = AE ·AC
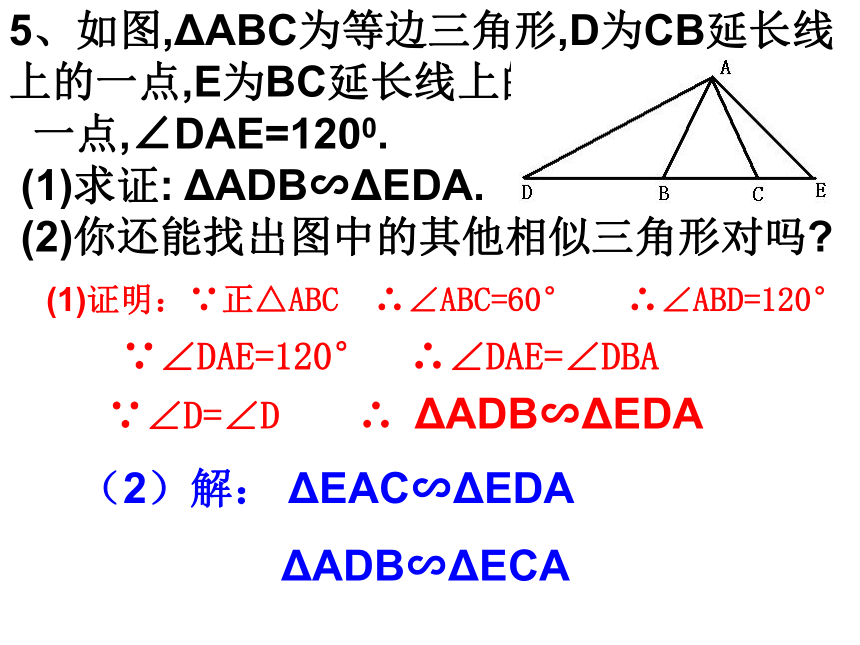
5、如图,ΔABC为等边三角形,D为CB延长线上的一点,E为BC延长线上的
一点,∠DAE=1200.
(1)求证: ΔADB∽ΔEDA.
(2)你还能找出图中的其他相似三角形对吗
(1)证明：∵正△ABC ∴∠ABC=60° ∴∠ABD=120°
∵∠DAE=120° ∴∠DAE=∠DBA
∵∠D=∠D ∴ ΔADB∽ΔEDA
（2）解： ΔEAC∽ΔEDA
ΔADB∽ΔECA
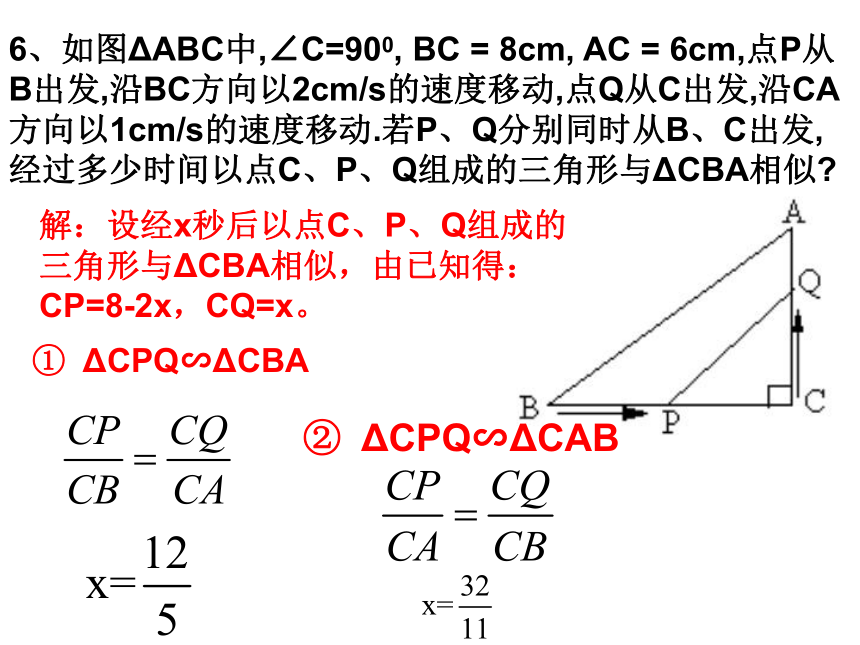
6、如图ΔABC中,∠C=900, BC = 8cm, AC = 6cm,点P从B出发,沿BC方向以2cm/s的速度移动,点Q从C出发,沿CA方向以1cm/s的速度移动.若P、Q分别同时从B、C出发,经过多少时间以点C、P、Q组成的三角形与ΔCBA相似
解：设经x秒后以点C、P、Q组成的三角形与ΔCBA相似，由已知得：CP=8-2x，CQ=x。
① ΔCPQ∽ΔCBA
② ΔCPQ∽ΔCAB
如图所示，AB∥CD，AB=2，CD=4，
则____________∽____________。
△ABO △DCO
OA:OD=________；
1:2
△ABO与△DCO的面积比为_________；
1:4
7、在△ABC中，AD是边BC上的中线，那么△ABD与△ADC的面积之比为___________；
1:1
理由
等底同高
8、在△ABC中，CD=2BD,则△ABD与△ADC的面积之比为___________；
1:2
9、在△ABC中，3CD=2BD,则△ABD与△ADC的面积之比为___________；
2:3
10、在梯形ABCD中，AD∥BC，AC与BD相交于点O。△AOD的面积等于4，△BOC的面积等于9.
（1）AD:BC=_______
（2）AO:CO=________
(3)△AOD与△COD的面积之比为___________；
(4) △COD的面积为_____
(5)梯形ABCD的面积为_____
2:3
2:3
2:3
6
25
11、平行四边形ABCD中，E在AD上，且AE=DE，CE交BD于点E，则BF：DF等于 （ ）
A、1：1 B、1：2
C、2：1 D、3：1
C
如图所示：有一边长为5cm的正方形ABCD和等腰⊿PQR，PQ=PR=5cm，QR=8cm，点B、C、Q、R在同一直线L上,从C、Q两点重合时，等腰⊿PQR以1cm/s的速度沿直线L按箭头所示方向开始匀速运动，t(s)后正方形ABCD与等腰⊿PQR重合部分为S（cm2）
⑴当t=3时，求的S值⑵当t=5时，求的S值
⑶当5s≤t ≤ 8s时，求S与t的函数解析式，并求出S的最大值