2.4二次函数的应用(3)课件ppt浙教版九年级上
文档属性
| 名称 | 2.4二次函数的应用(3)课件ppt浙教版九年级上 |
|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-11 00:00:00 | ||
图片预览



文档简介
(共36张PPT)
A
B
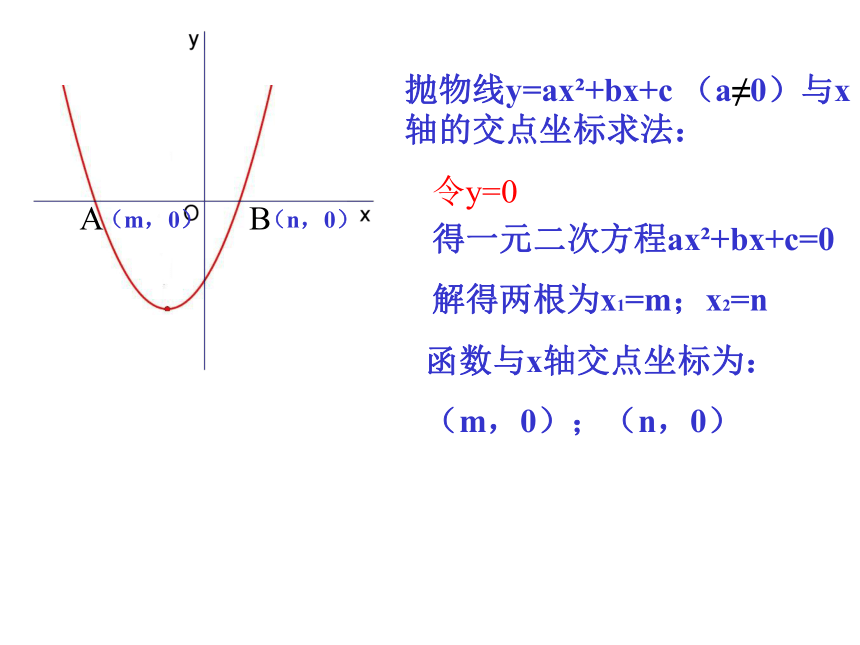
抛物线y=ax +bx+c (a≠0)与x轴的交点坐标求法:
令y=0
得一元二次方程ax +bx+c=0
解得两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
(m,0)
(n,0)
练习:求出下列二次函数和X轴的交点坐标:
y=x -2x+1 2. y=2x -4x+8
3. y=x -4x-8 4. y=3(x-4)(x+3)
1.y=X -4x+4
2.y=2X -x-1
3.y=3X -4x+6
看谁快
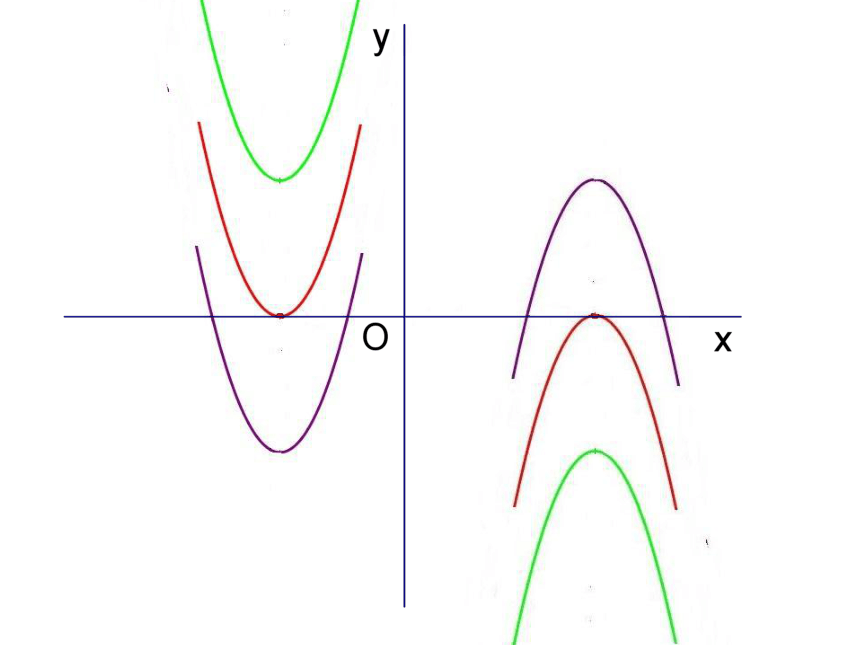
不用画图,试判断下列抛物线同x轴交点情况:
4.y=-9X -4x+3
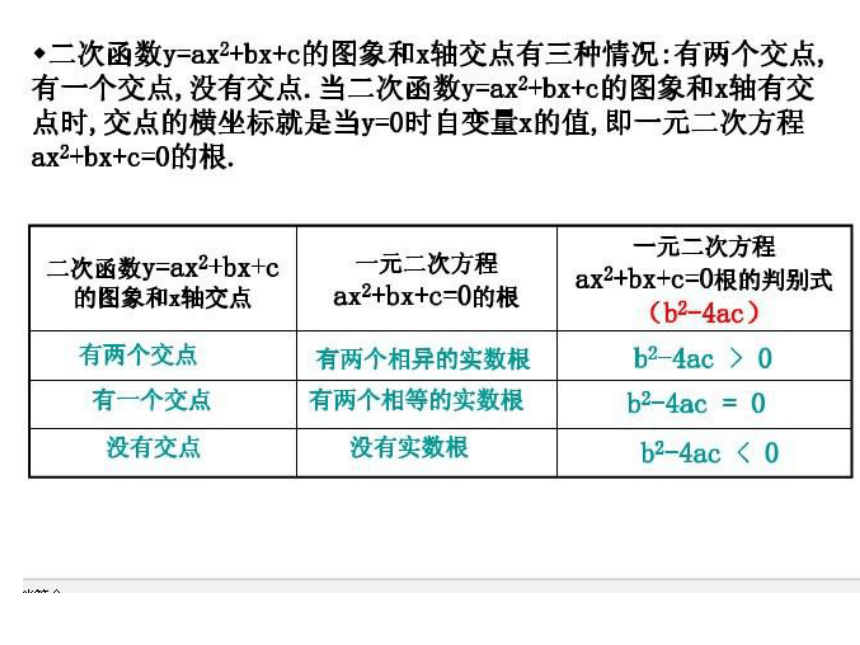
一个交点
两个交点
没有交点
两个交点
b2-4ac的符号
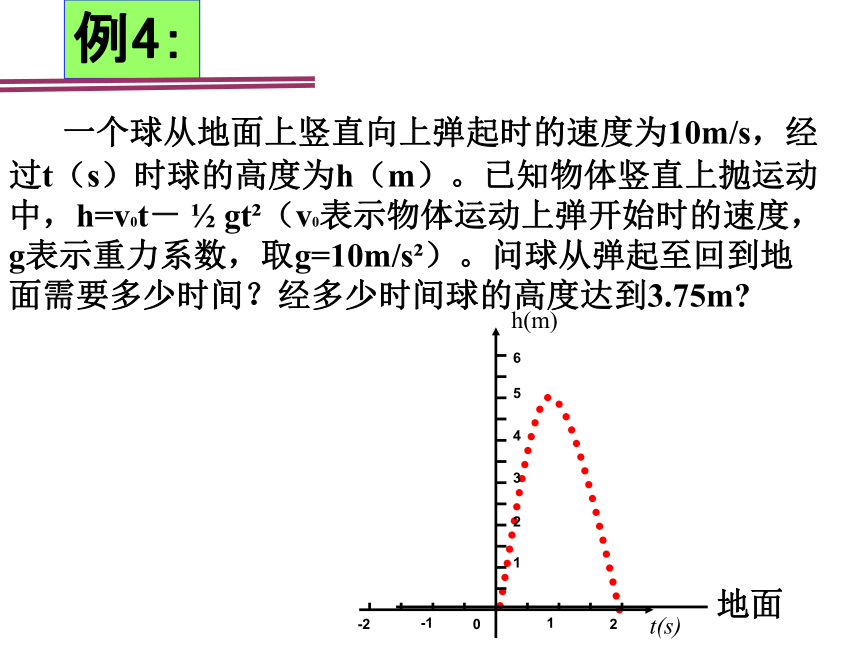
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
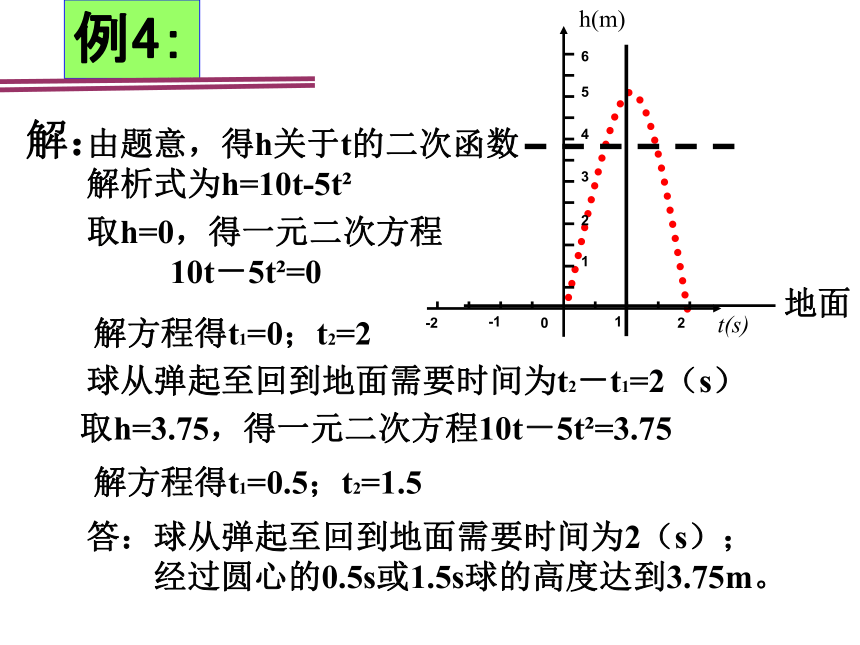
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
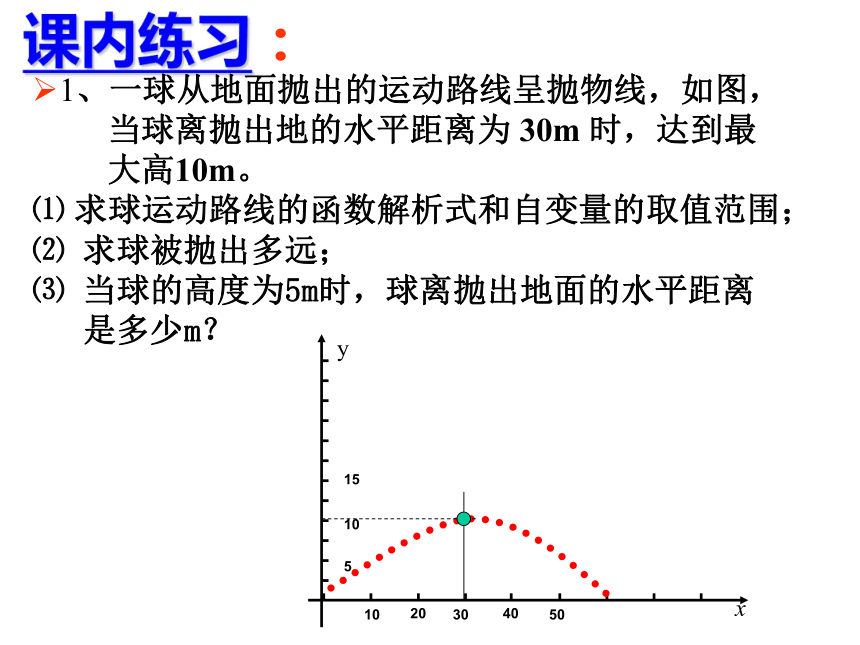
课内练习:
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
求出二次函数y=-x -2x+3图象的顶点坐标________与x轴的交点坐标_____________________并画出函数的大致图象.
(1,4)
(-3,0)
(1,0)
根据图像回答下列问题:
1.直接写出方程-x -2x+3=0的 解:
x1=-3;x2=1
2.令y=-5,得方程-x -2x+3=-5
解此方程得:
x1=-4;x2=2
y=-5
C
D
3.写出C和D点的坐标:
C(-4,-5) D(2,-5)
(-4,-5)
(2,-5)
填
空
根据图像回答下列问题:
1.一元二次方程 -x -2x+3=5有几个解?
y=5
无实数解
2.一元二次方程- x -2x+3=4有几个解?
y=4
两个相等的实数解
3.一元二次方程 -x -2x+3=-3有几个解?
y=-3
两个不相等的实数解
问:对于一元二次方程-x -2x+3 =m,当m为何值时,方程有两个不相等的实数解?当m为何值时,方程有两个相等的实数解?当m为何值时,方程没有实数解?
y= -x -2x+3、
课本例5:利用二次函数的图像求一元二次方程X +X-1= 0的近似解
y= X +X-1
课内练习
3.利用函数图象判断下列方程有没有解,有几个解。若有解,求出它们的解(精确到0.1)。
①X =2x-1 ②2x -x+1=0 ③2x -4x-1=0
y= x -2x+1
一解 x=1
②2x -x+1=0
y=2x -x+1
无解
③2x -4x-1=0
y=2x -4x-1
两解 x1=-0.2, x2=2.2
1、会运用一元二次方程求二次函数的图象与X轴或平行与X轴的直线的交点坐标,并用来解决相关的实际问题。
2、会用二次函数的图象求一元二次方程的解或近似解。
3、进一步体验在问题解决的过程中函数与方程两种数学模式经常需要互相转换。
一、教学目标:
1、会运用一元二次方程求二次函数的图象与X轴或平行与X轴的直线的交点坐标,并用来解决相关的实际问题。
2、会用二次函数的图象求一元二次方程的解或近似解。
3、进一步体验在问题解决的过程中函数与方程两种数学模式经常需要互相转换。
二、重点难点:
1、本节教学的重点是问题解决过程中二次函数与一元二次方程两种数学模式的互相转换。
2、本节例4涉及较多的“科学”知识,解题思路不易形成,是本节教学的难点。
课后反思
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
一.根据图像回答问题:
1.方程0.5x -x-4=0的解是什么?
2.方程0.5x -x-4=-6有几个解?
3.方程0.5x -x-4=-4.5有几个解?
y=0.6
2.对于一元二次方程0.5x -x-4=m,当m为何值时,方程有两个不相等的实数解?当m为何值时,方程有两个相等的实数解?当m为何值时,方程没有实数解?
4.方程0.5x -x-4=2有几个解
在本节的例5中,我们把一元二次方程X +X-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动:
y=x2
y=1-x
●
●
1未命名2.gsp
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
A
B
抛物线y=ax +bx+c (a≠0)与x轴的交点坐标求法:
令y=0
得一元二次方程ax +bx+c=0
解得两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
(m,0)
(n,0)
练习:求出下列二次函数和X轴的交点坐标:
y=x -2x+1 2. y=2x -4x+8
3. y=x -4x-8 4. y=3(x-4)(x+3)
1.y=X -4x+4
2.y=2X -x-1
3.y=3X -4x+6
看谁快
不用画图,试判断下列抛物线同x轴交点情况:
4.y=-9X -4x+3
一个交点
两个交点
没有交点
两个交点
b2-4ac的符号
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
课内练习:
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
求出二次函数y=-x -2x+3图象的顶点坐标________与x轴的交点坐标_____________________并画出函数的大致图象.
(1,4)
(-3,0)
(1,0)
根据图像回答下列问题:
1.直接写出方程-x -2x+3=0的 解:
x1=-3;x2=1
2.令y=-5,得方程-x -2x+3=-5
解此方程得:
x1=-4;x2=2
y=-5
C
D
3.写出C和D点的坐标:
C(-4,-5) D(2,-5)
(-4,-5)
(2,-5)
填
空
根据图像回答下列问题:
1.一元二次方程 -x -2x+3=5有几个解?
y=5
无实数解
2.一元二次方程- x -2x+3=4有几个解?
y=4
两个相等的实数解
3.一元二次方程 -x -2x+3=-3有几个解?
y=-3
两个不相等的实数解
问:对于一元二次方程-x -2x+3 =m,当m为何值时,方程有两个不相等的实数解?当m为何值时,方程有两个相等的实数解?当m为何值时,方程没有实数解?
y= -x -2x+3、
课本例5:利用二次函数的图像求一元二次方程X +X-1= 0的近似解
y= X +X-1
课内练习
3.利用函数图象判断下列方程有没有解,有几个解。若有解,求出它们的解(精确到0.1)。
①X =2x-1 ②2x -x+1=0 ③2x -4x-1=0
y= x -2x+1
一解 x=1
②2x -x+1=0
y=2x -x+1
无解
③2x -4x-1=0
y=2x -4x-1
两解 x1=-0.2, x2=2.2
1、会运用一元二次方程求二次函数的图象与X轴或平行与X轴的直线的交点坐标,并用来解决相关的实际问题。
2、会用二次函数的图象求一元二次方程的解或近似解。
3、进一步体验在问题解决的过程中函数与方程两种数学模式经常需要互相转换。
一、教学目标:
1、会运用一元二次方程求二次函数的图象与X轴或平行与X轴的直线的交点坐标,并用来解决相关的实际问题。
2、会用二次函数的图象求一元二次方程的解或近似解。
3、进一步体验在问题解决的过程中函数与方程两种数学模式经常需要互相转换。
二、重点难点:
1、本节教学的重点是问题解决过程中二次函数与一元二次方程两种数学模式的互相转换。
2、本节例4涉及较多的“科学”知识,解题思路不易形成,是本节教学的难点。
课后反思
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
一.根据图像回答问题:
1.方程0.5x -x-4=0的解是什么?
2.方程0.5x -x-4=-6有几个解?
3.方程0.5x -x-4=-4.5有几个解?
y=0.6
2.对于一元二次方程0.5x -x-4=m,当m为何值时,方程有两个不相等的实数解?当m为何值时,方程有两个相等的实数解?当m为何值时,方程没有实数解?
4.方程0.5x -x-4=2有几个解
在本节的例5中,我们把一元二次方程X +X-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动:
y=x2
y=1-x
●
●
1未命名2.gsp
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
同课章节目录
