二次函数的复习

(共33张PPT)
二 次 函 数 复 习
一、二次函数概念
形如y=ax2+bx+c (a,b,c是常数，a≠0) 的函数叫做二次函数
其中二次项为ax2，一次项为bx，常数项c
二次项的系数为a，一次项的系数为b，常数项c
(1)下列函数中，哪些是二次函数？
(1)y=3x-1 (2)y=3x2
(3)y=2x2-2x+1 (4)y=x2-x(1+x)
(2)当m取何值时，函数是y= (m+2)x
分别 是一次函数？ 反比例函数？
m2-2
二次函数？
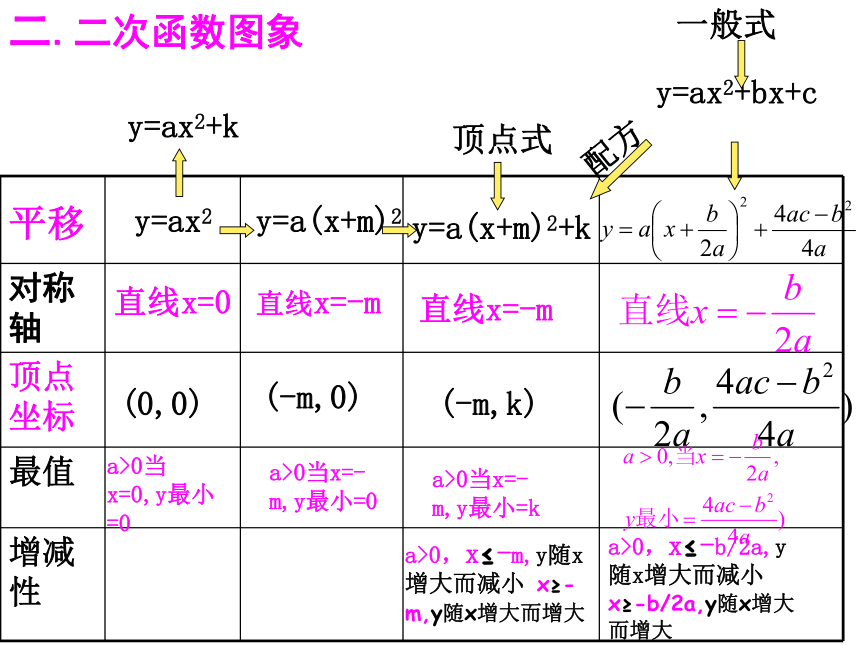
二.二次函数图象
对称轴
顶点坐标
最值
增减性
y=ax2
y=a(x+m)2
y=a(x+m)2+k
y=ax2+bx+c
y=ax2+k
顶点式
一般式
配方
平移
直线x=0
直线x=-m
直线x=-m
(0,0)
(-m,0)
(-m,k)
a>0当x=0,y最小=0
a>0当x=-m,y最小=0
a>0当x=-m,y最小=k
a>0，x≤-m,y随x增大而减小 x≥-m,y随x增大而增大
a>0，x≤-b/2a,y随x增大而减小 x≥-b/2a,y随x增大而增大
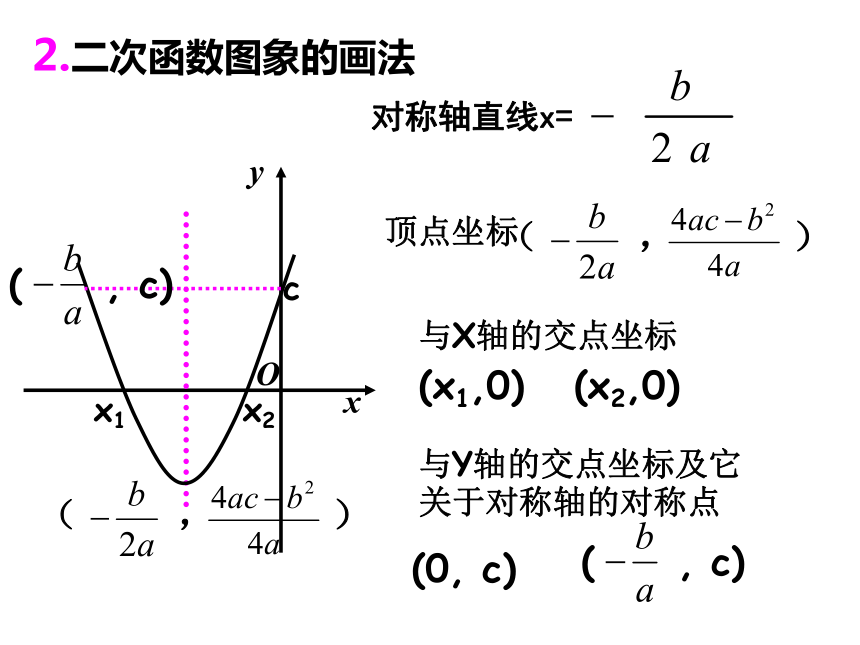
2.二次函数图象的画法
顶点坐标
与X轴的交点坐标
与Y轴的交点坐标及它关于对称轴的对称点
（ ， ）
(x1,0) (x2,0)
(0, c)
( , c)
（ ， ）
x1
x2
O
x
y
c
( , c)
对称轴直线x=
（1）画出y=x2-2x-3的图像
（2）画出y=2x2-2x-4的图像 （0≤x≤3）
做一做
(3)、将函数y=x2-4x+5转化成y=a(x+m)2+k的形式
(4)、将函数y=-2x2-4x+5转化成y=a(x+m)2+k的形式
(5) y=2(x+2)2是由 向 平移 个单位得到
(6) y=-2x2-2是由 向 平移 个单位得到
(7) y=-2(x-2)2+3是由 向 平移 个单位
，再向 平移 个单位得到
(8) y=2x2+4x-5是由 向 平移 个单位，再向 平移 个单位得到
(9) y=2x2向左平移2个单位，再向下平移3个单位得到
函数解析式是 。
y=2(x+2)2-3
y=2x2
左
2
y=-2x2
下
2
y=-2x2
右
2
上
3
y=2x2
左
1
下
7
（10）由函数y= -3(x-1)2+2的图象向右平移4个单位,再向上平移3个单位,得到的图象的函数解析式为_________________
y= - 3(x-1-4)2+2+3
（11）抛物线y=ax2向左平移一个单位,再向下平移8个单位且y=ax2过点(1,2).则平移后的解析式为______________;
y=2(x+1)2-8
（12）将抛物线y=x2-6x+4如何移动才能得到y=x2.
逆向思考,由y=x2-6x+4 =(x-3)2-5知:先向左平移3个单位,再向上平移5个单位.
（13）已知二次函数y=x2-4x-5 ，求下列问题
y=-2(x+1)2-8
①开口方向
②对称轴
③顶点坐标
③最值
④怎样平移
⑤x在什么范围，y随x增大而增大
⑥与坐标轴的交点坐标
⑧与x轴的交点坐标为A,B,与y轴的交点为C,则S ABC= .
⑨在抛物线上是否存在点P,使得S ABP是 ABC面积的2倍,若存在，请求出点P的坐标，若不存在，请说明理由
⑦当x为何值时，y>0
（14）已知二次函数y=x2+bx+c的顶点坐标（1，-2），求b，c的值
（15）已知二次函数y=x2+4x+c的顶点坐标在x轴上，求c的值
（16）已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上，求c的值
（17）已知二次函数y=x2+4x+c有最小值为2，求c的值
（18）已知二次函数y=-2x2+bx+c，当x=-2时函数有最大值为2，求b、c的值
2、已知抛物线顶点坐标（m, k），通常设抛物线解析式为_______________
3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________
1、已知抛物线上的三点，通常设解析式为________________
y=ax2+bx+c(a≠0)
y=a(x+m)2+k(a≠0)
y=a(x-x1)(x-x2) (a≠0)
如何求抛物线解析式常用的三种方法
一般式
顶点式
交点式或两根式
4.公式法
1.已知一个二次函数的图象经过点
（0，0），（1，﹣3），（2，﹣8）。
如何求下列条件下的二次函数的解析式:
3.已知二次函数的图象的对称轴是直线x=3,
并且经过点(6,0),和(2,12)
2.已知二次函数的图象的顶点坐标为
（－2，－3），且图象过点（－3，－2）。
4.矩形的周长为60，长为x，面积为y，则y关于x的函数关系式 。
如何判别a、b、c、b2-4ac，2a+b，a+b+c的符号
（1）a的符号：
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
（2）C的符号：
由抛物线与y轴的交点位置确定.
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
（3）b的符号：
由对称轴的位置确定
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
（4）b2-4ac的符号：
由抛物线与x轴的交点个数确定
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
（1）已知y=ax2+bx+c的图象如图所示,
a___0, b____0, c_____0, abc____0
b2-4ac_____0
a+b+c_____0, a-b+c____0
4a-2b+c_____0
0
-1
1
-2
＜
＜
＜
＞
＞
＞
＞
＞
x
y
O
A
x
y
O
B
x
y
O
C
x
y
O
D
（2）在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为（ ）
B
x
y
O
-1
1
（3）已知y=ax2+bx+c的图象如图所示,则下列说法正确的是（ ）
A abc>0
B a>0,b2-4ac<0
C 当x=1时，函数有最大值为-1
D 当x=1时，函数有最小值为-1
利用二次函数的图象求一元二次方程的近似解
1、根据下列表格的对应值：
判断方程ax2+bx+c=0（a≠0,a、b、c为常数）一个解的范围是　（　　　　）
Ａ、3＜x＜3.23 Ｂ、3.23＜x＜3.24
Ｃ、3.24＜x＜3.25 Ｄ、3.25＜x＜3.26
x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
1、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点，那么a的值和交点坐标分别为 。
9或1
2、写出一个开口向下，对称轴是直线x=3，且与y轴交于（0，-2）的抛物线解析式。
练一练
3、把抛物线y=-3x2绕着它的顶点旋转1800后所得的图象解析式是 。
y=3x2
4、已知二次函数y=a（x-h）2+k的图象过原点，最小值是-8，且形状与抛物线y=0.5x2-3x-5的形状相同，其解析式为 。
y=0.5（x-16）2-8
5、若x为任意实数，则二次函数y=x2+2x+3的函数值y的取值范围是 。
y≥2
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位，再向下平移2个单位得到的，则b= ，c= 。
7、已知抛物线y=2x2+bx+8的顶点在x轴上，则b= 。
8
3
±8
8、已知y=x2-（12-k）x+12，当x＞1时，y随x的增大而增大，当x＜1时，y随x的增大而减小，则k的值为 。
10
问题2这位同学身高1.7 m,若在这次跳投中，球在头顶上方0.25 m处出手，问：球出手时，他跳离地面的高度是多少？
x
y
o
1. 如图，有一次,我班某同学在距篮下4m处跳起投篮，球运行的路线是抛物线，当球运行的水平距离2.5m时，达到最大高度3.5m，然后准确落入篮圈。已知篮圈中心到地面的距离为3.05m.
3.05 m
2.5m
3.5m
问题1 建立如图所示的直角坐标系，求抛物线的解析式；
4 m
综合应用
2.你知道吗？平时我们在跳绳时，绳甩到最高处的形状可近似的看为抛物线，如图所示，正在甩绳的甲、乙两名学生拿绳的手间距为4米，距地面均为1米，学生丙、丁分别站在距甲拿绳的手水平距离1米、2.5米处，绳子甩到最高处时，刚好通过他们的头顶，已知学生丙的身高是1.5米，请你算一算学生丁的身高。
1m
2.5m
4m
1m
甲
乙
丙
丁
x
y
o
(0,1)
(4,1)
(1,1.5)
3.在矩形荒地ABCD中，AB=a，BC=b,（a>b > 0），今在四边上分别选取E、F、G、H四点，且AE=AH=CF=CG=x，建一个花园，如何设计，可使花园面积最大？
D
C
A
B
G
H
F
E
a
b
b
4. 如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
A
B
C
D
解：
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
(2)当x＝ 时，S最大值＝ ＝36（平方米）
∴ S＝x（24－4x）
＝－4x2＋24 x （0∴ 0<24－4x ≤8 4≤x<6
∴当x＝4m时，S最大值＝32 平方米
5.某企业投资100万元引进一条产品加工生产线，若不计维修、保养费用，预计投产后每年可创利33万。该生产线投产后，从第1年到第x年的维修、保养费用累计为y(万元)，且y=ax2+bx,若第1年的维修、保养 费用为2万元，到第2年为6万元。
　　（1）求y的解析式；
　　（2）投产后，这个企业在第几年就能收回投资？
解:（1）由题意，x=1时，y=2；x=2时，y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x.
　　（2）设g＝33x-100-x2-x,则
　　g=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时，g随x的增大而增大，故当x=4时，即第4年可收回投资。
6.某商场将进价40元一个的某种商品按50元一个售出时，能卖出500个，已知这种商品每个涨价一元，销量减少10个，为赚得最大利润，售价定为多少？最大利润是多少？
分析：利润=（每件商品所获利润）× （销售件数）
设每个涨价x元， 那么
（3）销售量可以表示为
（1）销售价可以表示为
（50+x）元（x≥ 0，且为整数）
(500-10x) 个
（2）一个商品所获利润可以表示为
（50+x-40）元
（4）共获利润可以表示为
(50+x-40)(500-10x)元
7. 如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式；
解：令y=0，则 –x+3=0，x=3，
∴B（3，0），
令x=0， 则y=3，
∴C（0，3），
b=2
c=3
｛
解得
-9+3b+c=0
c=3
｛
得
∴ y= -x2+2x+3
（3，0）
（0，3）
x
y
o
A
B
C
7.如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式；
（2）若抛物线的顶点为D，求四边形ABDC的面积；
（3，0）
（0，3）
B
C
D
x
y
o
A
E
（1，4）
（1，0）
（-1，0）
解：S四边形ABDC=S△AOC+S梯形OEDC+S △EBD
=9
= AO · OC + （OC+ED） · OE+ EB · ED
= × 1×3+ × （3+4） × 1+ × 3-1 ×4
7.如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（4）第（3）题改为在直线y= -x+3上是否存在点P，使S△PAC= S △PAB？若存在，求出点P的坐标；若不存在，说明理由。答案一样吗？
（3，0）
（0，3）
x
y
o
A
B
C
P
（3）若点P在直线 BC上且
S△PAC= S △PAB，求P的坐标；
Q
y
（3，0）
（0，3）
x
o
A
B
C
P
Q
P
（3，0）
（0，3）
x
y
o
A
B
C
Q