浙教版数学(八上)同步提高 第1章 三角形的初步认识 1.1-1.3证明同步测试(含答案)
文档属性
| 名称 | 浙教版数学(八上)同步提高 第1章 三角形的初步认识 1.1-1.3证明同步测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 847.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 21:04:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1章
三角形的初步认识
1.1-1.3同步测试
(含答案)
一、选择题(每小题3分,共30分)
1.下列线段能构成三角形的是(
)。
A.2,2,4
B.3,4.5
C.1,2,3
D.2,3,6
2.三角形的高(
)。
A.在边上
B.在三角形内
C.在三角形外
D.以上均有可能
3.可以用来证明命题“若x+2y=0,则x=y=0”是假命题的反例是(
)。
A.x=1,y=1
B.x=2,y=-1
C.x=-1,y=2
D.x=0,y=0
4.如图AB⊥AD,AB⊥BC则以AB为一条高线的三角形共有(
)。
A.1个
B.2个
C.3个
D.4个
5.已知:如图BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,
BC=12cm,则DE的长为(
)。
A.cm
B.cm
C.
4
cm
D.不能确定
6.在三角形中,最大的内角不能小于(
)。
A.30°
B.45°
C.60°
D.90°
7.下列命题中,真命题是(
)。
A.垂直于同一直线的两条直线平行
B.有两边和其中一边上的高对应相等的两个三角形全等
C.三角形三个内角中,至少有2个锐角
D.有两条边和一个角对应相等的两个三角形全等
8.三角形的周长为15cm,其中两边都等于第三边的两倍,那么这个三角形最短的边为(
)。
A.
1
cm
B
2
cm
C.
3
cm
D.
4
cm
9.在△ABC中,已知∠A=∠B+∠C,则△ABC是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
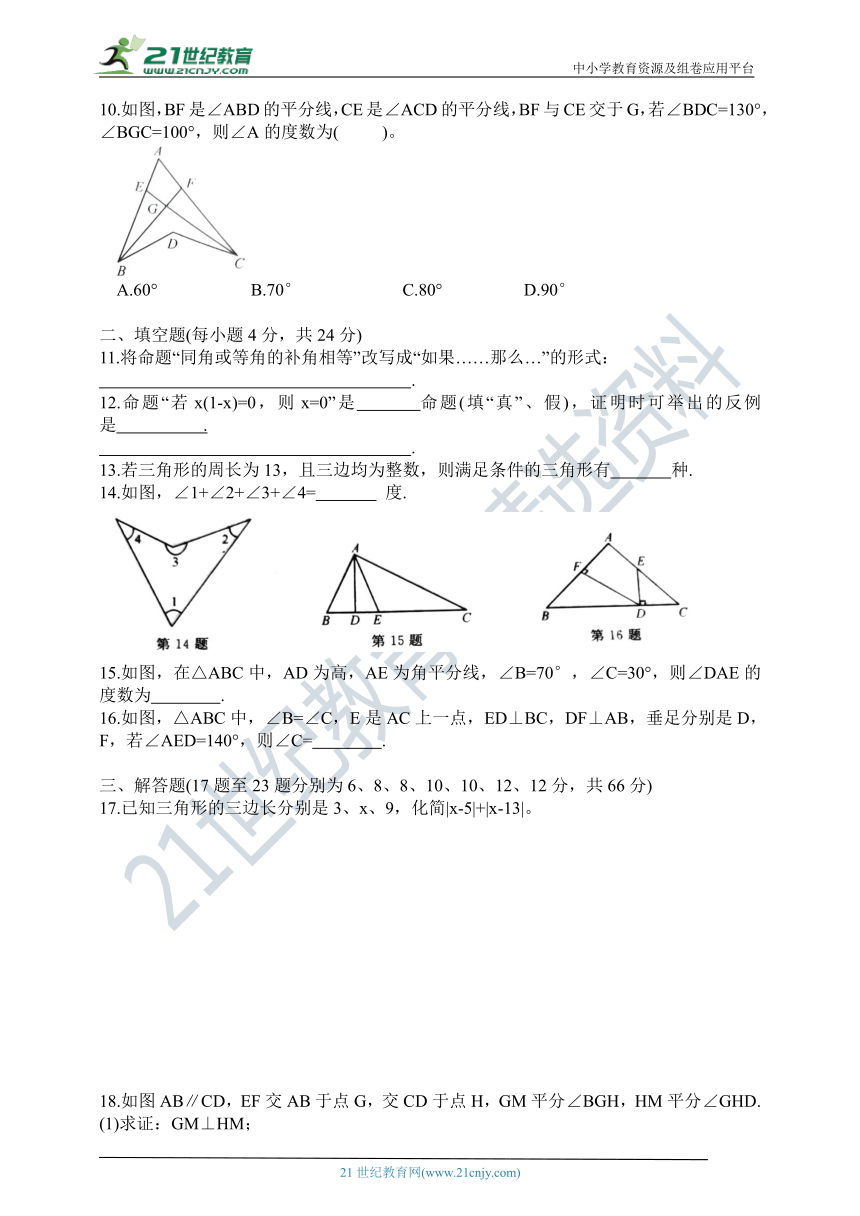
10.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为(
)。
A.60°
B.70°
C.80°
D.90°
二、填空题(每小题4分,共24分)
11.将命题“同角或等角的补角相等”改写成“如果……那么…”的形式:
.
12.命题“若x(1-x)=0,则x=0”是
命题(填“真”、假),证明时可举出的反例是
.
.
13.若三角形的周长为13,且三边均为整数,则满足条件的三角形有
种.
14.如图,∠1+∠2+∠3+∠4=
度.
15.如图,在△ABC中,AD为高,AE为角平分线,∠B=70°,∠C=30°,则∠DAE的度数为
.
16.如图,△ABC中,∠B=∠C,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别是D,F,若∠AED=140°,则∠C=
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.已知三角形的三边长分别是3、x、9,化简|x-5|+|x-13|。
18.如图AB∥CD,EF交AB于点G,交CD于点H,GM平分∠BGH,HM平分∠GHD.
(1)求证:GM⊥HM;
(2)用文字语言叙述这个命题.
19.如图,D是△ABC内任意一点,连结DA,DB,DC.
求证:DA+DB+DC>(AB+BC+CA).
20.如图,在△ABC中,AD是BC边上的高线,AF是△ABC的角平分线,∠BAC=100°,∠C=60°,求∠FAB、∠AFD、∠FAD的度数.
21.如图,已知∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE相交于点E.求证:∠E=∠A.
22.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,求∠BDC.
23.阅读以下材料并填空.平面上有n个点(n>2),且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数n和可连成直线的条数S.发现:
③推理:平面上有n个点,两点确定一条直线取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2,即.
④结论:.
试探究以下问题:
平面上有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少个不同的三角形?
(1)分析:当仅有3个点时,可作
个三角形;当有4个点时,可作
个三角形;当有5个点时,可作
个三角形;...
(2)归纳:考察点的个数n和可作出的三角形的个数S发现:(填下表)
点的个数
可作出的三角形的个数
点的个数
可作出的三角形的个数
3
4
5
...
...
n
(3)推理:
.
(4)结论:
.
第1章
三角形的初步认识
1.1-1.3同步测试
参考答案
一、选择题
1.B
2.D
3.B
4.D
5.A
6.C
7.C
8.C
9.B
10.B
二、填空题
11.如果两个角是同角或等角的补角,那么这两个角相等
12.假;x=1
13.5
14.360
15.20°
16.50°
三、解答题
17.解:∵三角形的三边长分别是3、x、9,
∴60,x-13<0,∴|x-5|+|x-13|=x-5+13-x=8,故答案为:8.
18.(1)略
(2)两条平行直线被第三条直线所截,同旁内角的平分线互相垂直
19.根据两边之和大于第三边
20.∠FAB=50°;∠AFD=70°;∠FAD=20°
证明:∵∠ACD是△ABC的外角,∴∠ACD=∠A+∠ABC,
∵CE平分∠ACD,∴∠ECD=(∠A+∠ABC).
又∠ECD是△BEC的外角,∴∠ECD=∠E+∠EBC,
∴∠E+∠EBC=(∠A+∠ABC).
∵BE平分∠ABC,∴∠EBC=∠ABC,∴∠E+∠ABC=(∠A+∠ABC),
∴∠E=∠A.
22.△ABC中,∠ACB=90°,∠A=22°,∠B=90°-∠A=68°,
由折叠的性质可得:∠CED=∠B=68°,∠BDC=∠EDC,
∴∠ADE=∠CED-∠A=46°,∴∠BDC==67°。
23.(1);;;
(2)略
(3)平面上有n个点,过不在同一直线上的三点可以确定一个三角形,取第一个顶点A有n种取法,取第二个顶点B有(n-1)种取法,取第三个顶点C有(n-2)种取法,所以一共有n(n-1)(n-2)个三角形,但△ABC,△ACB.△BAC,△BCA,△CAB,△CBA都是同一个三角形,故应除以6,即;
(4)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第1章
三角形的初步认识
1.1-1.3同步测试
(含答案)
一、选择题(每小题3分,共30分)
1.下列线段能构成三角形的是(
)。
A.2,2,4
B.3,4.5
C.1,2,3
D.2,3,6
2.三角形的高(
)。
A.在边上
B.在三角形内
C.在三角形外
D.以上均有可能
3.可以用来证明命题“若x+2y=0,则x=y=0”是假命题的反例是(
)。
A.x=1,y=1
B.x=2,y=-1
C.x=-1,y=2
D.x=0,y=0
4.如图AB⊥AD,AB⊥BC则以AB为一条高线的三角形共有(
)。
A.1个
B.2个
C.3个
D.4个
5.已知:如图BD是∠ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,
BC=12cm,则DE的长为(
)。
A.cm
B.cm
C.
4
cm
D.不能确定
6.在三角形中,最大的内角不能小于(
)。
A.30°
B.45°
C.60°
D.90°
7.下列命题中,真命题是(
)。
A.垂直于同一直线的两条直线平行
B.有两边和其中一边上的高对应相等的两个三角形全等
C.三角形三个内角中,至少有2个锐角
D.有两条边和一个角对应相等的两个三角形全等
8.三角形的周长为15cm,其中两边都等于第三边的两倍,那么这个三角形最短的边为(
)。
A.
1
cm
B
2
cm
C.
3
cm
D.
4
cm
9.在△ABC中,已知∠A=∠B+∠C,则△ABC是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
10.如图,BF是∠ABD的平分线,CE是∠ACD的平分线,BF与CE交于G,若∠BDC=130°,∠BGC=100°,则∠A的度数为(
)。
A.60°
B.70°
C.80°
D.90°
二、填空题(每小题4分,共24分)
11.将命题“同角或等角的补角相等”改写成“如果……那么…”的形式:
.
12.命题“若x(1-x)=0,则x=0”是
命题(填“真”、假),证明时可举出的反例是
.
.
13.若三角形的周长为13,且三边均为整数,则满足条件的三角形有
种.
14.如图,∠1+∠2+∠3+∠4=
度.
15.如图,在△ABC中,AD为高,AE为角平分线,∠B=70°,∠C=30°,则∠DAE的度数为
.
16.如图,△ABC中,∠B=∠C,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别是D,F,若∠AED=140°,则∠C=
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.已知三角形的三边长分别是3、x、9,化简|x-5|+|x-13|。
18.如图AB∥CD,EF交AB于点G,交CD于点H,GM平分∠BGH,HM平分∠GHD.
(1)求证:GM⊥HM;
(2)用文字语言叙述这个命题.
19.如图,D是△ABC内任意一点,连结DA,DB,DC.
求证:DA+DB+DC>(AB+BC+CA).
20.如图,在△ABC中,AD是BC边上的高线,AF是△ABC的角平分线,∠BAC=100°,∠C=60°,求∠FAB、∠AFD、∠FAD的度数.
21.如图,已知∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE相交于点E.求证:∠E=∠A.
22.如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,求∠BDC.
23.阅读以下材料并填空.平面上有n个点(n>2),且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数n和可连成直线的条数S.发现:
③推理:平面上有n个点,两点确定一条直线取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2,即.
④结论:.
试探究以下问题:
平面上有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少个不同的三角形?
(1)分析:当仅有3个点时,可作
个三角形;当有4个点时,可作
个三角形;当有5个点时,可作
个三角形;...
(2)归纳:考察点的个数n和可作出的三角形的个数S发现:(填下表)
点的个数
可作出的三角形的个数
点的个数
可作出的三角形的个数
3
4
5
...
...
n
(3)推理:
.
(4)结论:
.
第1章
三角形的初步认识
1.1-1.3同步测试
参考答案
一、选择题
1.B
2.D
3.B
4.D
5.A
6.C
7.C
8.C
9.B
10.B
二、填空题
11.如果两个角是同角或等角的补角,那么这两个角相等
12.假;x=1
13.5
14.360
15.20°
16.50°
三、解答题
17.解:∵三角形的三边长分别是3、x、9,
∴6
18.(1)略
(2)两条平行直线被第三条直线所截,同旁内角的平分线互相垂直
19.根据两边之和大于第三边
20.∠FAB=50°;∠AFD=70°;∠FAD=20°
证明:∵∠ACD是△ABC的外角,∴∠ACD=∠A+∠ABC,
∵CE平分∠ACD,∴∠ECD=(∠A+∠ABC).
又∠ECD是△BEC的外角,∴∠ECD=∠E+∠EBC,
∴∠E+∠EBC=(∠A+∠ABC).
∵BE平分∠ABC,∴∠EBC=∠ABC,∴∠E+∠ABC=(∠A+∠ABC),
∴∠E=∠A.
22.△ABC中,∠ACB=90°,∠A=22°,∠B=90°-∠A=68°,
由折叠的性质可得:∠CED=∠B=68°,∠BDC=∠EDC,
∴∠ADE=∠CED-∠A=46°,∴∠BDC==67°。
23.(1);;;
(2)略
(3)平面上有n个点,过不在同一直线上的三点可以确定一个三角形,取第一个顶点A有n种取法,取第二个顶点B有(n-1)种取法,取第三个顶点C有(n-2)种取法,所以一共有n(n-1)(n-2)个三角形,但△ABC,△ACB.△BAC,△BCA,△CAB,△CBA都是同一个三角形,故应除以6,即;
(4)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
