浙教版数学(八上)单元测评AB卷 第1章 三角形的初步认识A卷(含答案)
文档属性
| 名称 | 浙教版数学(八上)单元测评AB卷 第1章 三角形的初步认识A卷(含答案) | 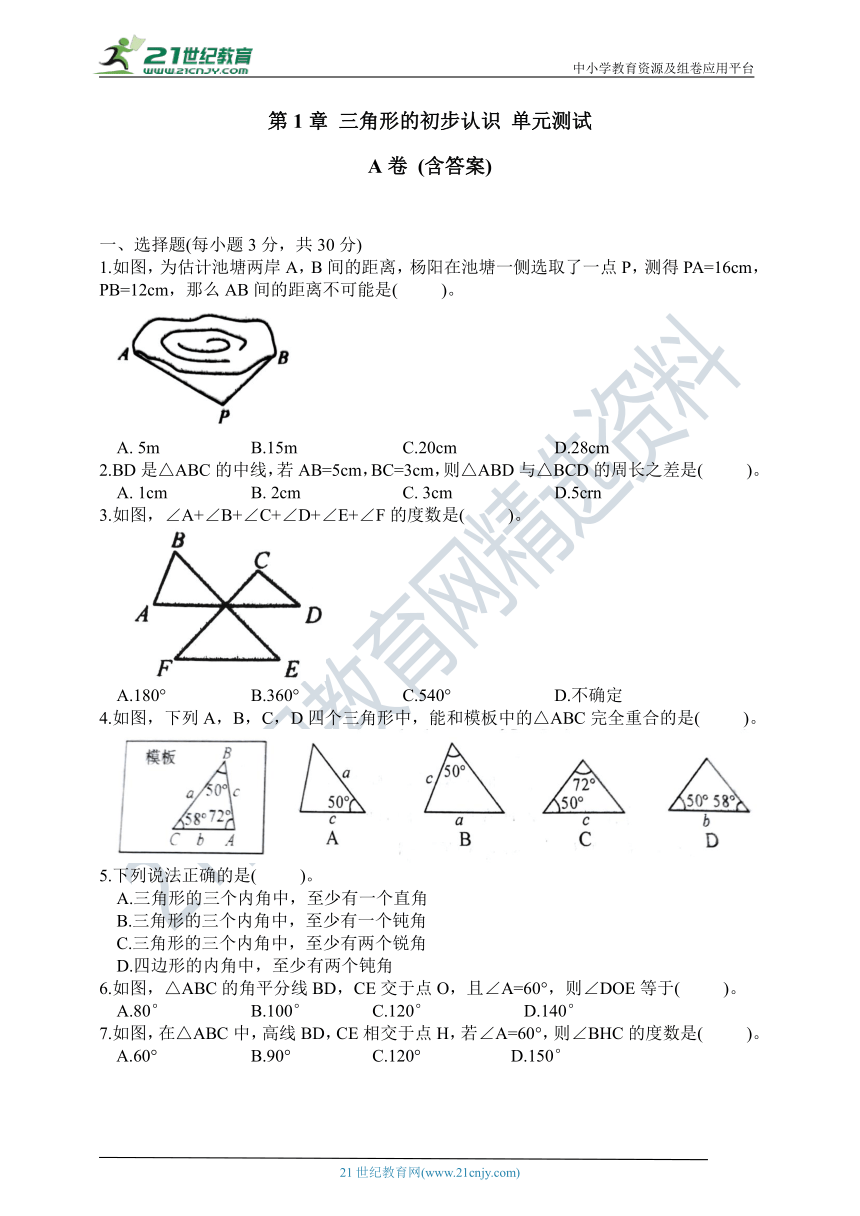 | |
| 格式 | zip | ||
| 文件大小 | 944.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 21:19:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1章
三角形的初步认识
单元测试
A卷
(含答案)
一、选择题(每小题3分,共30分)
1.如图,为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12cm,那么AB间的距离不可能是(
)。
A.
5m
B.15m
C.20cm
D.28cm
2.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是(
)。
A.
1cm
B.
2cm
C.
3cm
D.5crn
3.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(
)。
A.180°
B.360°
C.540°
D.不确定
4.如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是(
)。
5.下列说法正确的是(
)。
A.三角形的三个内角中,至少有一个直角
B.三角形的三个内角中,至少有一个钝角
C.三角形的三个内角中,至少有两个锐角
D.四边形的内角中,至少有两个钝角
6.如图,△ABC的角平分线BD,CE交于点O,且∠A=60°,则∠DOE等于(
)。
A.80°
B.100°
C.120°
D.140°
7.如图,在△ABC中,高线BD,CE相交于点H,若∠A=60°,则∠BHC的度数是(
)。
A.60°
B.90°
C.120°
D.150°
8.如图所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E。某同学分析图形后得出以下结论:
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE,上述结论一定正确的是(
)。
A.①②③
B.②③④
C.①③⑤
D.①③④
9.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是(
)。
A.边角边
B.角边角
C.边边边
D.边边角
10.如图所示,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形则下列结论不一定成立的是(
)。
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
二、填空题(每小题4分共24分)
11.已知命题:“如果两个三角形全等那么这两个三角形的面积相等.”写出它的逆命题
,该逆命题是
命题(填“真”或“假”)。
12.如图,已知∠DAE=∠CAE,∠DBE=∠CBE,则图中共有全等三角形
对,请分别写出来
。
13.如图,△ABC中,DE⊥BC于E,AF⊥BC于F.已知△BCD与△ABC的面积之比为1:3,DE=3cm,则AF=
。
14.已知三角形的三边长分别是3、x、9,则化简|x-5|+|x-13|=
。
15.在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是
。
16.如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形。正确的有:
。
三、解答题(17题至23题分别为688、10、10、12、12分,共66分)
17.七年级某班的篮球啦啦队同学,为了在明天比赛中给同学加油助威,提前制作了同一规格的彩旗。小明在放学回家后,发现自己的彩旗破损了一角他想用彩纸重新制作一面彩旗(如图所示),请你帮助小明,用直尺和圆规在彩纸上作出一个与破损前完全一样的三角形,并解释你作图的理由。
理由:
。
18.小明做了一个如图所示的风筝,他想去验证∠BAC与∠DAC是否相等,手头只有一把尺子(足够长),你能帮助他想个方法吗?说明你这样做的理由。
19.如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,求证:BD=2CE。
20.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC。
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数。
21.如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E点,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC。
22如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE。请完整说明为何△ABC与△DEC全等的理由。
23.请你找一个长方形的纸片,按以下步骤进行动手操作:
步骤一:在CD上取一点P,将角D和角C向上翻折,这样将形成折痕PM和PN,如图甲所示;
步骤二:翻折后,使点D,C落在原长方形所在的平面内,即点D'和C',细心调整折痕PN,PM的位置使PD',PC'重合如图乙,设折角∠MPD'=α,∠NPC'=β。
(1)猜想∠MPN的度数;
(2)若重复上面的操作过程,并改变α的大小,猜想:随着α的大小变化,∠MPN的度数怎样变化?并说明你猜想的正确性。
第1章
三角形的初步认识(A卷)
参考答案
一、选择题
1.D
2.B
3.B
4.A
5.C
6.C
7.C
8.D
9.B
10.D
二、填空题
11.
如果两个三角形的面积相等,那么这两个三角形全等;假
12.
3,△ABD≌△ABC,△DBE≌△CBE,△ADE≌△ACE
13.
9cm
14.
8
15.
116.
①②③④
三、解答题
17.画图略,理由:有两角和它们的夹边对应相等的两个三角形全等
18.用尺子量出AB,AD,BC,CD的长度,若AB=AD,BC=CD,则∠BAC=∠DAC,因为当AB=AD,BC=CD时,另有AC=AC,则△ABC≌△ADC.
由此可得∠BAC=∠DAC.
19.证明:延长CE与BA的延长线交于点F,
∵∠BAC=90°,CE⊥BD,∴∠BAC=∠DEC,∵∠ADB=∠CDE,∴∠ABD=∠DCE,在△BAD和△CAF中:∠BAD=∠CAF,AB=AC,∠ABD=∠DCE,
∴△BAD≌△CAF(ASA),∴BD=CF。
在△BEF和△BEC中:∠1=∠2,BE=BE,∠BEF=∠BEC,∴△BEF≌△BEC(ASA),
∴CE=EF,∴DB=2CE.
20.(1)∵∠ABC=90°,D为AB延长线上一点,∠ABE=∠CBD=90°,在△ABE和△CBD中:AB=CB,∠ABE=∠CBD,BE=BD,∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,∴∠CAB=45°,∵∠CAE=30°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
∵△ABE≌△CBD,∴∠BCD=∠BAE=15°,
∴∠BDC=90°-∠BCD=90°-15°=75°。
21.解:(1)证明:在四边形ABCD中,∵∠A=∠BCD=90°,∴∠B+∠ADC=180°.
又∵∠ADC+∠EDC=180°,∴∠ABC=∠EDC.
(2)证明:连结AC.在△ABC和△EDC中:BC=DC,∠ABC=∠EDC,AB=ED,
∴△ABC≌△EDC.
22.∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,
在△ACD中,∠ACD=90°,∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,∴∠1=∠D,
在△ABC和△DEC中:∠1=∠D,∠3=∠5,BC=CE,∴△ABC≌△DEC(AAS)方法不唯一。
23.(1)90°
(2)∠MPN的度数不变,仍为90°(提示:∠a=∠MPD,∠β=∠NPC,又∵∠a+∠β+∠MPD+∠NPC=180°,∴a+β=90°)。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第1章
三角形的初步认识
单元测试
A卷
(含答案)
一、选择题(每小题3分,共30分)
1.如图,为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16cm,PB=12cm,那么AB间的距离不可能是(
)。
A.
5m
B.15m
C.20cm
D.28cm
2.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是(
)。
A.
1cm
B.
2cm
C.
3cm
D.5crn
3.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是(
)。
A.180°
B.360°
C.540°
D.不确定
4.如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是(
)。
5.下列说法正确的是(
)。
A.三角形的三个内角中,至少有一个直角
B.三角形的三个内角中,至少有一个钝角
C.三角形的三个内角中,至少有两个锐角
D.四边形的内角中,至少有两个钝角
6.如图,△ABC的角平分线BD,CE交于点O,且∠A=60°,则∠DOE等于(
)。
A.80°
B.100°
C.120°
D.140°
7.如图,在△ABC中,高线BD,CE相交于点H,若∠A=60°,则∠BHC的度数是(
)。
A.60°
B.90°
C.120°
D.150°
8.如图所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E。某同学分析图形后得出以下结论:
①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE,上述结论一定正确的是(
)。
A.①②③
B.②③④
C.①③⑤
D.①③④
9.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是(
)。
A.边角边
B.角边角
C.边边边
D.边边角
10.如图所示,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形则下列结论不一定成立的是(
)。
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
二、填空题(每小题4分共24分)
11.已知命题:“如果两个三角形全等那么这两个三角形的面积相等.”写出它的逆命题
,该逆命题是
命题(填“真”或“假”)。
12.如图,已知∠DAE=∠CAE,∠DBE=∠CBE,则图中共有全等三角形
对,请分别写出来
。
13.如图,△ABC中,DE⊥BC于E,AF⊥BC于F.已知△BCD与△ABC的面积之比为1:3,DE=3cm,则AF=
。
14.已知三角形的三边长分别是3、x、9,则化简|x-5|+|x-13|=
。
15.在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是
。
16.如图所示,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下面结论中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的点到B,C两点的距离相等;④图中共有3对全等三角形。正确的有:
。
三、解答题(17题至23题分别为688、10、10、12、12分,共66分)
17.七年级某班的篮球啦啦队同学,为了在明天比赛中给同学加油助威,提前制作了同一规格的彩旗。小明在放学回家后,发现自己的彩旗破损了一角他想用彩纸重新制作一面彩旗(如图所示),请你帮助小明,用直尺和圆规在彩纸上作出一个与破损前完全一样的三角形,并解释你作图的理由。
理由:
。
18.小明做了一个如图所示的风筝,他想去验证∠BAC与∠DAC是否相等,手头只有一把尺子(足够长),你能帮助他想个方法吗?说明你这样做的理由。
19.如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,求证:BD=2CE。
20.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE,DC。
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数。
21.如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E点,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC。
22如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE。请完整说明为何△ABC与△DEC全等的理由。
23.请你找一个长方形的纸片,按以下步骤进行动手操作:
步骤一:在CD上取一点P,将角D和角C向上翻折,这样将形成折痕PM和PN,如图甲所示;
步骤二:翻折后,使点D,C落在原长方形所在的平面内,即点D'和C',细心调整折痕PN,PM的位置使PD',PC'重合如图乙,设折角∠MPD'=α,∠NPC'=β。
(1)猜想∠MPN的度数;
(2)若重复上面的操作过程,并改变α的大小,猜想:随着α的大小变化,∠MPN的度数怎样变化?并说明你猜想的正确性。
第1章
三角形的初步认识(A卷)
参考答案
一、选择题
1.D
2.B
3.B
4.A
5.C
6.C
7.C
8.D
9.B
10.D
二、填空题
11.
如果两个三角形的面积相等,那么这两个三角形全等;假
12.
3,△ABD≌△ABC,△DBE≌△CBE,△ADE≌△ACE
13.
9cm
14.
8
15.
1
①②③④
三、解答题
17.画图略,理由:有两角和它们的夹边对应相等的两个三角形全等
18.用尺子量出AB,AD,BC,CD的长度,若AB=AD,BC=CD,则∠BAC=∠DAC,因为当AB=AD,BC=CD时,另有AC=AC,则△ABC≌△ADC.
由此可得∠BAC=∠DAC.
19.证明:延长CE与BA的延长线交于点F,
∵∠BAC=90°,CE⊥BD,∴∠BAC=∠DEC,∵∠ADB=∠CDE,∴∠ABD=∠DCE,在△BAD和△CAF中:∠BAD=∠CAF,AB=AC,∠ABD=∠DCE,
∴△BAD≌△CAF(ASA),∴BD=CF。
在△BEF和△BEC中:∠1=∠2,BE=BE,∠BEF=∠BEC,∴△BEF≌△BEC(ASA),
∴CE=EF,∴DB=2CE.
20.(1)∵∠ABC=90°,D为AB延长线上一点,∠ABE=∠CBD=90°,在△ABE和△CBD中:AB=CB,∠ABE=∠CBD,BE=BD,∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,∴∠CAB=45°,∵∠CAE=30°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
∵△ABE≌△CBD,∴∠BCD=∠BAE=15°,
∴∠BDC=90°-∠BCD=90°-15°=75°。
21.解:(1)证明:在四边形ABCD中,∵∠A=∠BCD=90°,∴∠B+∠ADC=180°.
又∵∠ADC+∠EDC=180°,∴∠ABC=∠EDC.
(2)证明:连结AC.在△ABC和△EDC中:BC=DC,∠ABC=∠EDC,AB=ED,
∴△ABC≌△EDC.
22.∵∠BCE=∠ACD=90°,∴∠3+∠4=∠4+∠5,∴∠3=∠5,
在△ACD中,∠ACD=90°,∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,∴∠1=∠D,
在△ABC和△DEC中:∠1=∠D,∠3=∠5,BC=CE,∴△ABC≌△DEC(AAS)方法不唯一。
23.(1)90°
(2)∠MPN的度数不变,仍为90°(提示:∠a=∠MPD,∠β=∠NPC,又∵∠a+∠β+∠MPD+∠NPC=180°,∴a+β=90°)。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
