浙教版数学(八上)单元测评AB卷 第1章 三角形的初步认识B卷(含答案)
文档属性
| 名称 | 浙教版数学(八上)单元测评AB卷 第1章 三角形的初步认识B卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 902.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 21:20:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第1章
三角形的初步认识
单元测试
B卷
(含答案)
一、选择题(每小题3分,共30分)
1.一个三角形三个内角的度数之比为2:3:5,这个三角形一定是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
2.下列说法:①全等三角形的面积相等;②全等三角形的周长相等;③全等三角形的对应角相等;④全等三角形的对应边相等。其中正确的有(
)。
A.1个
B.2个
C.3个
D.4个
3.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解”,小华根据小明的提示作出的图形正确的是(
)。
4.如图所示,∠A,∠1,∠2的大小关系是(
)。
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
5.如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是(
)。
A.24°
B.30°
C.32°
D.36°
6.根据下列已知条件,能唯一画出△ABC的是(
)。
A.
AB=3,
BC=4,AC=8
B.∠A=60°,∠B=45°,AB=4
C.
AB=3,BC=3,∠A=30°
D.∠C=90°,AB=6
7.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是(
)。
A.
AB=AC
B.
BD=CD
C.∠B=∠C
D.∠BDA=∠CDA
8.将一副直角三角板,按如图所示叠放在一起,则图中∠a的度数是(
)。
A.45°
B.60°
C.75°
D.90°
9.用尺规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是
(
)。
A.
SSS
B.
ASA
C.
AAS
D.角平分线上的点到角两边距离相等
10.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是(
)。
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④.
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题4分,共24分)
11.如图,△ABC中,∠1+∠2+∠3=
度,∠4+∠5+∠6
度.
12.如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于D.若DC=3,则点D到AB的距离是
.
13.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A,∠1,∠2之间有一种数量关系始终保持不变,这种关系是
.
14.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:
①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的是
.
15.如图在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为
cm.
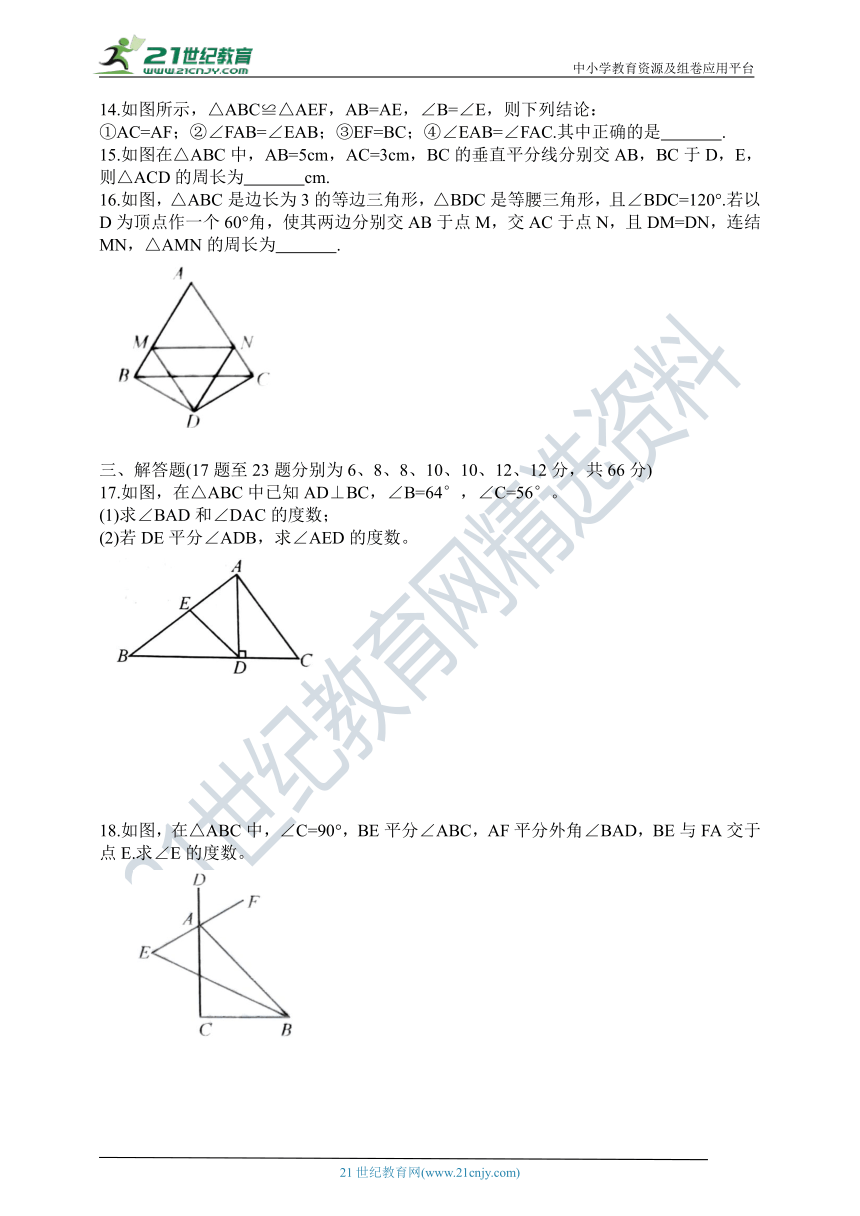
16.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.若以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,且DM=DN,连结MN,△AMN的周长为
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.如图,在△ABC中已知AD⊥BC,∠B=64°,∠C=56°。
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数。
18.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E.求∠E的度数。
19.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
20.如图,在△ABC中,AC=6cm,AB=9cm,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2cm,BD=3cm.求:
(1)线段BC的长;
(2)若∠ACB的平分线CF交AD于点O,且O到AC的距离是acm,请用含a的代数式表示△ABC的面积.
21.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连结BD,
CE。
(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由。
22.已知:如图,△ABC的三个内角平分线交于O点,过O作OE⊥BC于E.
求证:∠BOD=∠COE。
23.已知,在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连结DE,DE所在直线交直线BC于点M.请探究:
(1)如图①,当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论;
(2)如图②,当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由。
第1章
三角形的初步认识(B卷)
参考答案
一、选择题
1.B
2.D
3.C
4.B
5.C
6.B
7.B
8.C
9.A
10.D
二、填空题
11.180
360
12.3
13.2∠A=∠1+∠2
14.①③④
15.8
16.6
三、解答题
17.(1)AD⊥BC,∴∠B+∠BAD=90°,∠C+∠CAD=90°,∵∠B=64°,∠C=56°,
∴∠BAD=90°-∠B=90-64°=26°,∠DAC=90°-∠C=90°-56°=34°.
(2)∵DE平分∠ADB,∴∠EDB=∠ADB=45°,
∠AED是△BDB的一外角,∴∠AED=∠B+∠BDE=61°+45°=109°.
18.∠E=45°
19.(1)30°
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°,∴∠ECD=90°.
∴∠ACD=∠ECD.
在△ACD与△ECD中:AC=EC,∠ACD=∠ECD,CD=CD,
∴△ACD≌△ECD(SAS).∴DA=DE。
20.(1)BC=5cm
(2)10a
cm2
21.(1)∵△ABC,△ADE是等腰直角三角形,∴AB=AC,∠BAD=∠EAC=90°,
AD=AE∴△ADB≌△AEC(SAS)∴BD=CE
∵△ADB≌△AEC∴∴∠ACE=∠DBA,
而∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°.
(3)同样成立.BD=CE,且两线段所在直线互相垂直.即∠BFC=90°,
∴三角形全等还是成立.
∵△ABC,△ADE是等腰直角三角形,∴AB=AC,AD=AE.
且∠BAC=∠EAD,∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
∴利用SAS得到△ADB≌△AEC,得到BD=CE,∠BFC也等于90°不变。
22.通过计算可得∠BOD=∠COE=90°-∠ACB。
23.(1)DM=EM:证明:过点E作EF∥AB交BC于点F,
∵AB=AC,∴:∠ABC=∠C;
又∵EF∥AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC∴EF=BD.
又∵EF∥AB,∴∠ADM=∠MEF.
在△DBM和△EFM中,∠BDE=∠FEM,∠BMD=∠FME,BD=EF,
∴△DBM≌△EFM.∴DM=EM。
(2)成立:证明:过点E作EF∥AB交CB的延长线于点F,
∴AB=AC,∠ABC=∠C;
又∵EF∥AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC,EF=BD.又∵EF∥AB,∴∠ADM=∠MEF.
在△DBM和△EFM中,∠BDE=∠FEM,∠BMD=∠FME,BD=EF,
∴△DBM≌△EFM∴DM=EM。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第1章
三角形的初步认识
单元测试
B卷
(含答案)
一、选择题(每小题3分,共30分)
1.一个三角形三个内角的度数之比为2:3:5,这个三角形一定是(
)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
2.下列说法:①全等三角形的面积相等;②全等三角形的周长相等;③全等三角形的对应角相等;④全等三角形的对应边相等。其中正确的有(
)。
A.1个
B.2个
C.3个
D.4个
3.小华在电话中问小明:“已知一个三角形三边长分别是4,9,12如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解”,小华根据小明的提示作出的图形正确的是(
)。
4.如图所示,∠A,∠1,∠2的大小关系是(
)。
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
5.如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是(
)。
A.24°
B.30°
C.32°
D.36°
6.根据下列已知条件,能唯一画出△ABC的是(
)。
A.
AB=3,
BC=4,AC=8
B.∠A=60°,∠B=45°,AB=4
C.
AB=3,BC=3,∠A=30°
D.∠C=90°,AB=6
7.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是(
)。
A.
AB=AC
B.
BD=CD
C.∠B=∠C
D.∠BDA=∠CDA
8.将一副直角三角板,按如图所示叠放在一起,则图中∠a的度数是(
)。
A.45°
B.60°
C.75°
D.90°
9.用尺规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是
(
)。
A.
SSS
B.
ASA
C.
AAS
D.角平分线上的点到角两边距离相等
10.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是(
)。
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④.
A.1个
B.2个
C.3个
D.4个
二、填空题(每小题4分,共24分)
11.如图,△ABC中,∠1+∠2+∠3=
度,∠4+∠5+∠6
度.
12.如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于D.若DC=3,则点D到AB的距离是
.
13.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A,∠1,∠2之间有一种数量关系始终保持不变,这种关系是
.
14.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:
①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC.其中正确的是
.
15.如图在△ABC中,AB=5cm,AC=3cm,BC的垂直平分线分别交AB,BC于D,E,则△ACD的周长为
cm.
16.如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.若以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,且DM=DN,连结MN,△AMN的周长为
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.如图,在△ABC中已知AD⊥BC,∠B=64°,∠C=56°。
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数。
18.如图,在△ABC中,∠C=90°,BE平分∠ABC,AF平分外角∠BAD,BE与FA交于点E.求∠E的度数。
19.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
20.如图,在△ABC中,AC=6cm,AB=9cm,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2cm,BD=3cm.求:
(1)线段BC的长;
(2)若∠ACB的平分线CF交AD于点O,且O到AC的距离是acm,请用含a的代数式表示△ABC的面积.
21.以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连结BD,
CE。
(1)说明BD=CE;
(2)延长BD,交CE于点F,求∠BFC的度数;
(3)若如图2放置,上面的结论还成立吗?请简单说明理由。
22.已知:如图,△ABC的三个内角平分线交于O点,过O作OE⊥BC于E.
求证:∠BOD=∠COE。
23.已知,在等腰△ABC中,AB=AC,在射线CA上截取线段CE,在射线AB上截取线段BD,连结DE,DE所在直线交直线BC于点M.请探究:
(1)如图①,当点E在线段AC上,点D在AB延长线上时,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论;
(2)如图②,当点E在CA的延长线上,点D在AB的延长线上时,若BD=CE,则(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由。
第1章
三角形的初步认识(B卷)
参考答案
一、选择题
1.B
2.D
3.C
4.B
5.C
6.B
7.B
8.C
9.A
10.D
二、填空题
11.180
360
12.3
13.2∠A=∠1+∠2
14.①③④
15.8
16.6
三、解答题
17.(1)AD⊥BC,∴∠B+∠BAD=90°,∠C+∠CAD=90°,∵∠B=64°,∠C=56°,
∴∠BAD=90°-∠B=90-64°=26°,∠DAC=90°-∠C=90°-56°=34°.
(2)∵DE平分∠ADB,∴∠EDB=∠ADB=45°,
∠AED是△BDB的一外角,∴∠AED=∠B+∠BDE=61°+45°=109°.
18.∠E=45°
19.(1)30°
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°,∴∠ECD=90°.
∴∠ACD=∠ECD.
在△ACD与△ECD中:AC=EC,∠ACD=∠ECD,CD=CD,
∴△ACD≌△ECD(SAS).∴DA=DE。
20.(1)BC=5cm
(2)10a
cm2
21.(1)∵△ABC,△ADE是等腰直角三角形,∴AB=AC,∠BAD=∠EAC=90°,
AD=AE∴△ADB≌△AEC(SAS)∴BD=CE
∵△ADB≌△AEC∴∴∠ACE=∠DBA,
而∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°.
(3)同样成立.BD=CE,且两线段所在直线互相垂直.即∠BFC=90°,
∴三角形全等还是成立.
∵△ABC,△ADE是等腰直角三角形,∴AB=AC,AD=AE.
且∠BAC=∠EAD,∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
∴利用SAS得到△ADB≌△AEC,得到BD=CE,∠BFC也等于90°不变。
22.通过计算可得∠BOD=∠COE=90°-∠ACB。
23.(1)DM=EM:证明:过点E作EF∥AB交BC于点F,
∵AB=AC,∴:∠ABC=∠C;
又∵EF∥AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC∴EF=BD.
又∵EF∥AB,∴∠ADM=∠MEF.
在△DBM和△EFM中,∠BDE=∠FEM,∠BMD=∠FME,BD=EF,
∴△DBM≌△EFM.∴DM=EM。
(2)成立:证明:过点E作EF∥AB交CB的延长线于点F,
∴AB=AC,∠ABC=∠C;
又∵EF∥AB,∴∠ABC=∠EFC,∴∠EFC=∠C,∴EF=EC.
又∵BD=EC,EF=BD.又∵EF∥AB,∴∠ADM=∠MEF.
在△DBM和△EFM中,∠BDE=∠FEM,∠BMD=∠FME,BD=EF,
∴△DBM≌△EFM∴DM=EM。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
