浙教版数学(八上)同步提高 第2章 特殊三角形 2.1-2.4等腰三角形的判定定理同步测试(含答案)
文档属性
| 名称 | 浙教版数学(八上)同步提高 第2章 特殊三角形 2.1-2.4等腰三角形的判定定理同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 995.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2章
特殊三角形
2.1-2.4同步测试
(含答案)
一、选择题(每小题3分,共30分)
1.若等腰三角形的顶角为40°,则它的底角度数为(
)。
A.40°
B.50°
C.60°
D.70°
2.在射线、角和等腰三角形中,它们中的轴对称图形有(
)。
A.都是
B.只有一个是
C.只有一个不是
D.都不是
3.如图在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为(
)。
A.35°
B.40°
C.45°
D.50°
4.三角形内有一点它到三角形三边的距离都相等,同时与三角形三顶点的距离也都相等,则这个三角形一定是(
)。
A.等腰三角形
B.等腰直角三角形
C.非等腰三角形
D.等边三角形
5.△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B=(
)。
A.70°
B.20°或70°
C.40°或70°
D.40°或20°
6.已知等腰三角形的一边长为5cm,另一边长为6cm,则它的周长为(
)。
A.1
cm
B.17cm
C.
16
cm
D.16cm或17cm
7.如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点,若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数为何?(
)。
8.如图在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=(
)。
A.30°
B.45°
C.60°
D.90°
9.同学们都玩过跷跷板的游戏,如图所示,是一跷跷板的示意图,立柱OC与地面垂直,OA=OB.当跷跷板的一头A着地时,∠OAC=25°,则当跷晓板的另一头B着地时,∠AOA’等于(
)。
A.25°
B.50°
C.60°
D.130°
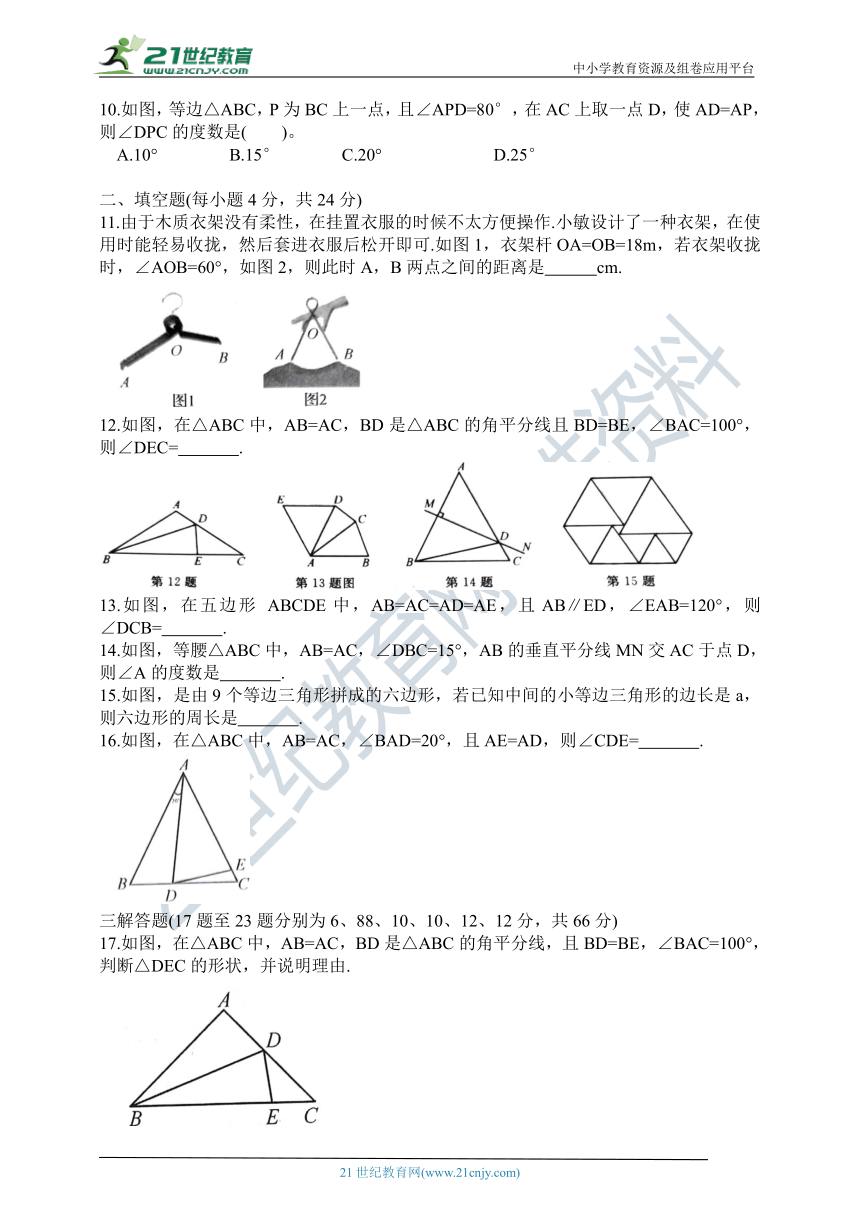
10.如图,等边△ABC,P为BC上一点,且∠APD=80°,在AC上取一点D,使AD=AP,则∠DPC的度数是(
)。
A.10°
B.15°
C.20°
D.25°
二、填空题(每小题4分,共24分)
11.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18m,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是
cm.
12.如图,在△ABC中,AB=AC,BD是△ABC的角平分线且BD=BE,∠BAC=100°,则∠DEC=
.
13.如图,在五边形
ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=
.
14.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是
.
15.如图,是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是a,则六边形的周长是
.
16.如图,在△ABC中,AB=AC,∠BAD=20°,且AE=AD,则∠CDE=
.
三解答题(17题至23题分别为6、88、10、10、12、12分,共66分)
17.如图,在△ABC中,AB=AC,BD是△ABC的角平分线,且BD=BE,∠BAC=100°,判断△DEC的形状,并说明理由.
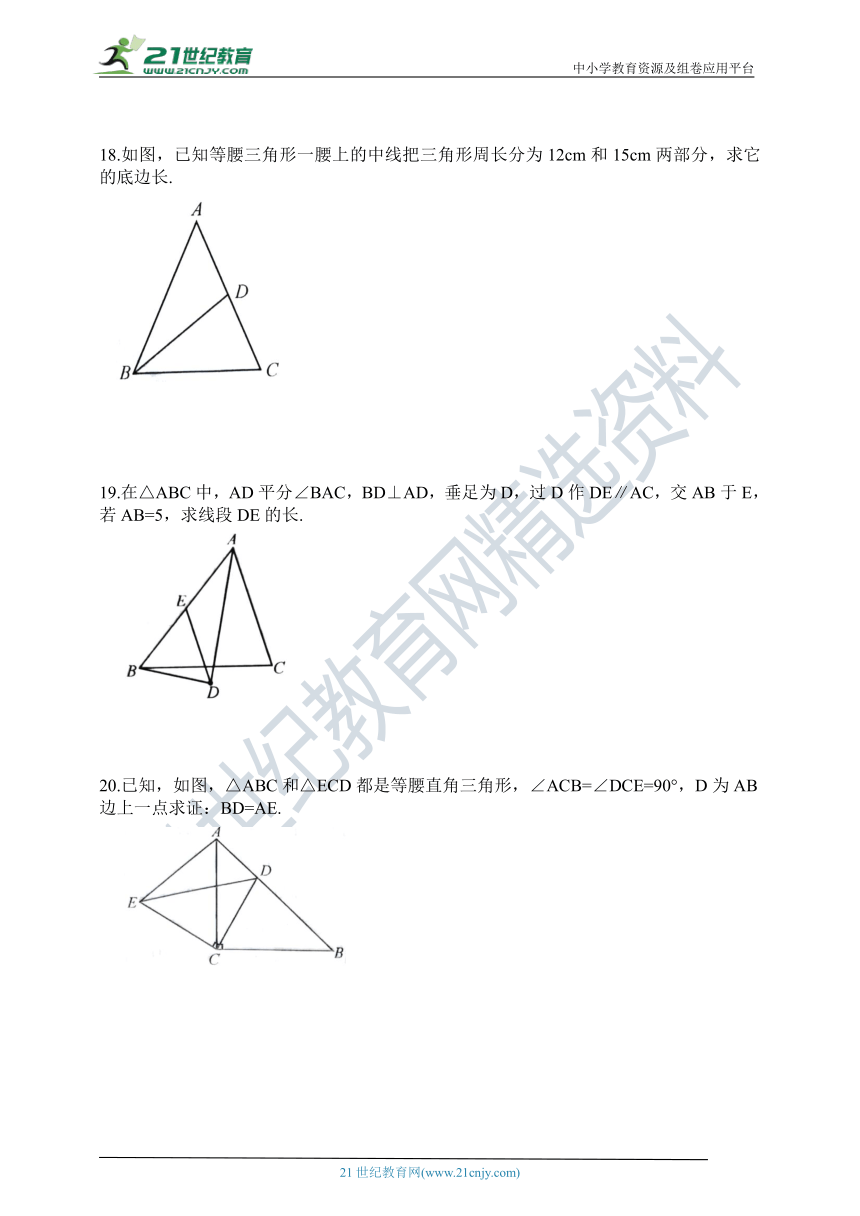
18.如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边长.
19.在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
20.已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点求证:BD=AE.
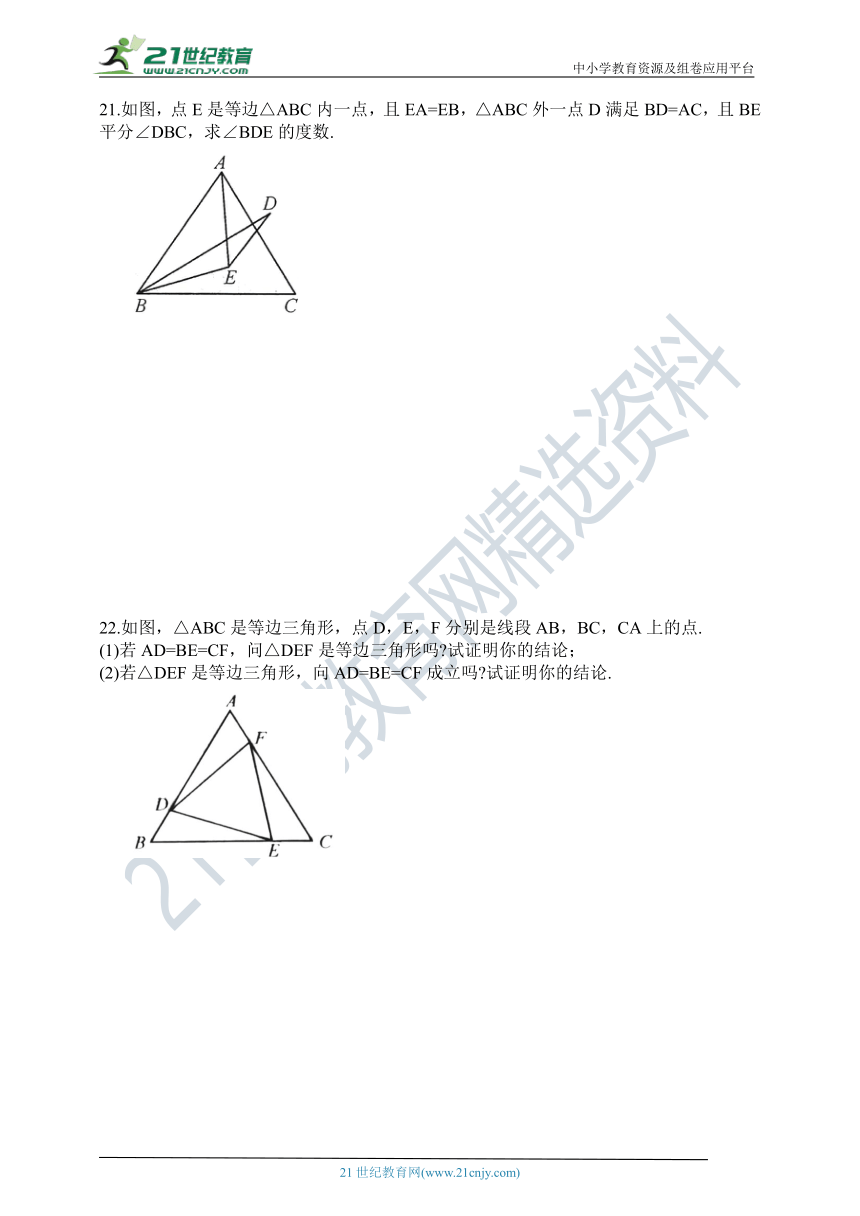
21.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.
22.如图,△ABC是等边三角形,点D,E,F分别是线段AB,BC,CA上的点.
(1)若AD=BE=CF,问△DEF是等边三角形吗?试证明你的结论;
(2)若△DEF是等边三角形,向AD=BE=CF成立吗?试证明你的结论.
23.小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线ab所成角的度数.
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
第2章
特殊三角形
2.1-2.4参考答案
一、选择题
1.D
2.A
3.A
4.D
5.B
6.D
7.B
8.B
9.B
10.C
二、填空题
11.18
12.100°
13.150°
14.50°
15.30a
16.10°
三、解答题
17.等腰三角形,理由略
18.7cm或11cm
19.(1)∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,
∵AD⊥DB,∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,∴DE=BE,
∵AB=5,∴DE=BE=AE=AB=2.5。
20.∵△ABC和△ECD都是等腰直角三角形,∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,∴∠ACE+∠ACD=∠BCD+∠ACD,∴∠ACE=∠BCD。
在△ACE和△BCD中:AC=
BC,∠ACE=∠BCD,
CD=CE,
∴△ACE≌△BCD(SAS),BD=AE。
21.连结CE,说明△ACE≌△BCE得∠BCE=∠ACE=30°.
同时说明△BCE≌△BDE得∠BDE=∠BCE=30°.
22.(1)△DEF是等边三角形,提示证△ADF≌△BED≌△CFE.即得△DEF是等边三角形;
(2)AD=BE=CF成立.证明略
23.(1)PC∥a(两直线平行,同位角相等);
(2)∠PAB=∠PDA=∠BDC=∠1,
如图,∵PA=PD,∴∠PAB=∠PDA,∵∠BDC=∠PDA(对顶角相等),
又∵PC∥a,∴∠PDA=∠1,∴∠PAB=∠PDA=∠BDC=∠1;
(3)如图,作线段AB的垂直平分线EF,则EF是所求作的图形。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第2章
特殊三角形
2.1-2.4同步测试
(含答案)
一、选择题(每小题3分,共30分)
1.若等腰三角形的顶角为40°,则它的底角度数为(
)。
A.40°
B.50°
C.60°
D.70°
2.在射线、角和等腰三角形中,它们中的轴对称图形有(
)。
A.都是
B.只有一个是
C.只有一个不是
D.都不是
3.如图在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为(
)。
A.35°
B.40°
C.45°
D.50°
4.三角形内有一点它到三角形三边的距离都相等,同时与三角形三顶点的距离也都相等,则这个三角形一定是(
)。
A.等腰三角形
B.等腰直角三角形
C.非等腰三角形
D.等边三角形
5.△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B=(
)。
A.70°
B.20°或70°
C.40°或70°
D.40°或20°
6.已知等腰三角形的一边长为5cm,另一边长为6cm,则它的周长为(
)。
A.1
cm
B.17cm
C.
16
cm
D.16cm或17cm
7.如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点,若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数为何?(
)。
8.如图在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=(
)。
A.30°
B.45°
C.60°
D.90°
9.同学们都玩过跷跷板的游戏,如图所示,是一跷跷板的示意图,立柱OC与地面垂直,OA=OB.当跷跷板的一头A着地时,∠OAC=25°,则当跷晓板的另一头B着地时,∠AOA’等于(
)。
A.25°
B.50°
C.60°
D.130°
10.如图,等边△ABC,P为BC上一点,且∠APD=80°,在AC上取一点D,使AD=AP,则∠DPC的度数是(
)。
A.10°
B.15°
C.20°
D.25°
二、填空题(每小题4分,共24分)
11.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18m,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是
cm.
12.如图,在△ABC中,AB=AC,BD是△ABC的角平分线且BD=BE,∠BAC=100°,则∠DEC=
.
13.如图,在五边形
ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=
.
14.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是
.
15.如图,是由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是a,则六边形的周长是
.
16.如图,在△ABC中,AB=AC,∠BAD=20°,且AE=AD,则∠CDE=
.
三解答题(17题至23题分别为6、88、10、10、12、12分,共66分)
17.如图,在△ABC中,AB=AC,BD是△ABC的角平分线,且BD=BE,∠BAC=100°,判断△DEC的形状,并说明理由.
18.如图,已知等腰三角形一腰上的中线把三角形周长分为12cm和15cm两部分,求它的底边长.
19.在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
20.已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点求证:BD=AE.
21.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.
22.如图,△ABC是等边三角形,点D,E,F分别是线段AB,BC,CA上的点.
(1)若AD=BE=CF,问△DEF是等边三角形吗?试证明你的结论;
(2)若△DEF是等边三角形,向AD=BE=CF成立吗?试证明你的结论.
23.小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线ab所成角的度数.
(1)请写出这种做法的理由;
(2)小明在此基础上又进行了如下操作和探究(如图3):①以P为圆心,任意长为半径画圆弧,分别交直线b,PC于点A,D;②连结AD并延长交直线a于点B,请写出图3中所有与∠PAB相等的角,并说明理由;
(3)请在图3画板内作出“直线a,b所成的跑到画板外面去的角”的平分线(画板内的部分),只要求作出图形,并保留作图痕迹.
第2章
特殊三角形
2.1-2.4参考答案
一、选择题
1.D
2.A
3.A
4.D
5.B
6.D
7.B
8.B
9.B
10.C
二、填空题
11.18
12.100°
13.150°
14.50°
15.30a
16.10°
三、解答题
17.等腰三角形,理由略
18.7cm或11cm
19.(1)∵AD平分∠BAC,∴∠BAD=∠CAD,
∵DE∥AC,∴∠CAD=∠ADE,∴∠BAD=∠ADE,∴AE=DE,
∵AD⊥DB,∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,∴DE=BE,
∵AB=5,∴DE=BE=AE=AB=2.5。
20.∵△ABC和△ECD都是等腰直角三角形,∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,∴∠ACE+∠ACD=∠BCD+∠ACD,∴∠ACE=∠BCD。
在△ACE和△BCD中:AC=
BC,∠ACE=∠BCD,
CD=CE,
∴△ACE≌△BCD(SAS),BD=AE。
21.连结CE,说明△ACE≌△BCE得∠BCE=∠ACE=30°.
同时说明△BCE≌△BDE得∠BDE=∠BCE=30°.
22.(1)△DEF是等边三角形,提示证△ADF≌△BED≌△CFE.即得△DEF是等边三角形;
(2)AD=BE=CF成立.证明略
23.(1)PC∥a(两直线平行,同位角相等);
(2)∠PAB=∠PDA=∠BDC=∠1,
如图,∵PA=PD,∴∠PAB=∠PDA,∵∠BDC=∠PDA(对顶角相等),
又∵PC∥a,∴∠PDA=∠1,∴∠PAB=∠PDA=∠BDC=∠1;
(3)如图,作线段AB的垂直平分线EF,则EF是所求作的图形。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
