浙教版数学(八上)同步提高 第2章 特殊三角形 2.5-2.8 直角三角形全等的判定同步测试(含答案)
文档属性
| 名称 | 浙教版数学(八上)同步提高 第2章 特殊三角形 2.5-2.8 直角三角形全等的判定同步测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 917.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-31 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2章
特殊三角形
2.5-2.8
同步测试
(含答案)
一、选择题(每小题3分,共30分)
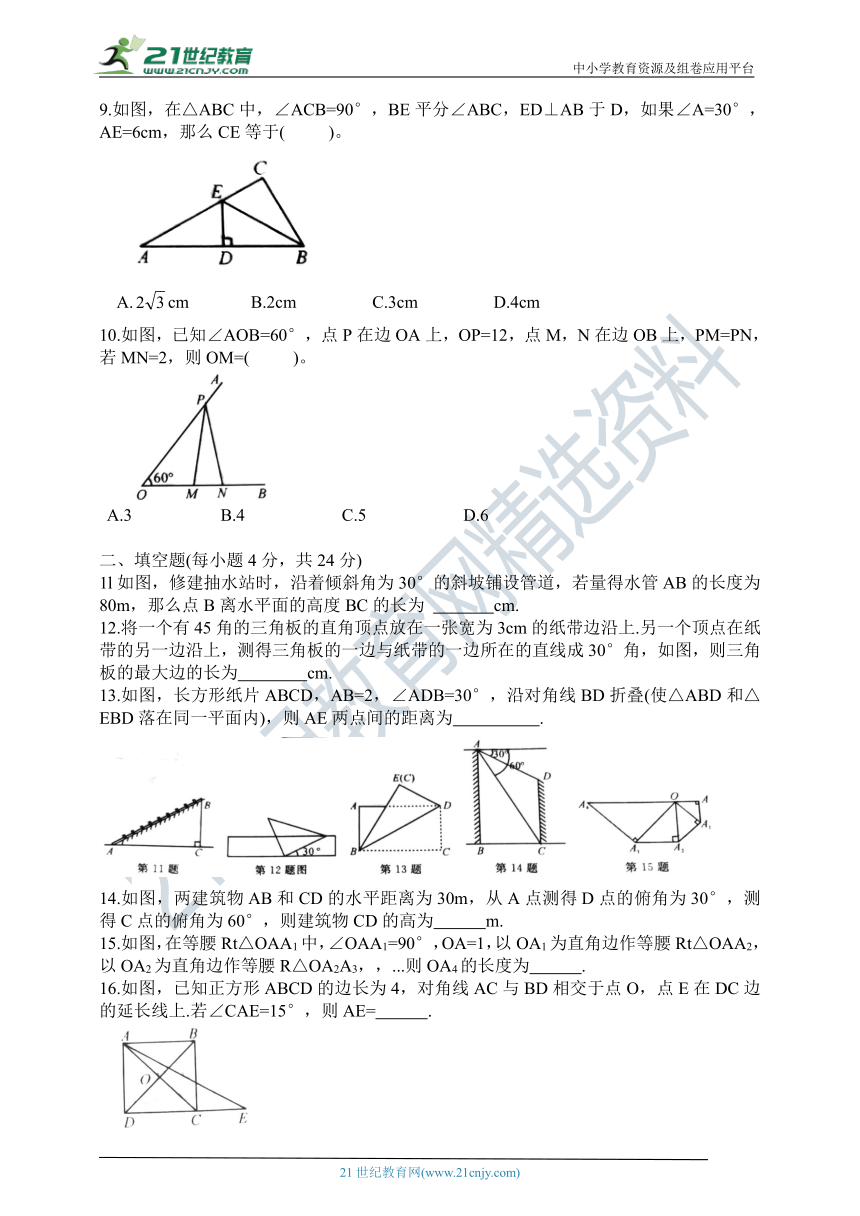
1.如图,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是(
)。
A.10°
B.20°
C.30°
D.40°
2.将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CED’=60°,则∠AED的大小是(
)。
A.60°
B.50°
C.75°
D.55°
3.如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为(
)。
A.a
B.
2a
C.a
D.
a
4.如图,CD是Rt△ABC斜边上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
A.25°
B.30°
C.45°
D.60°
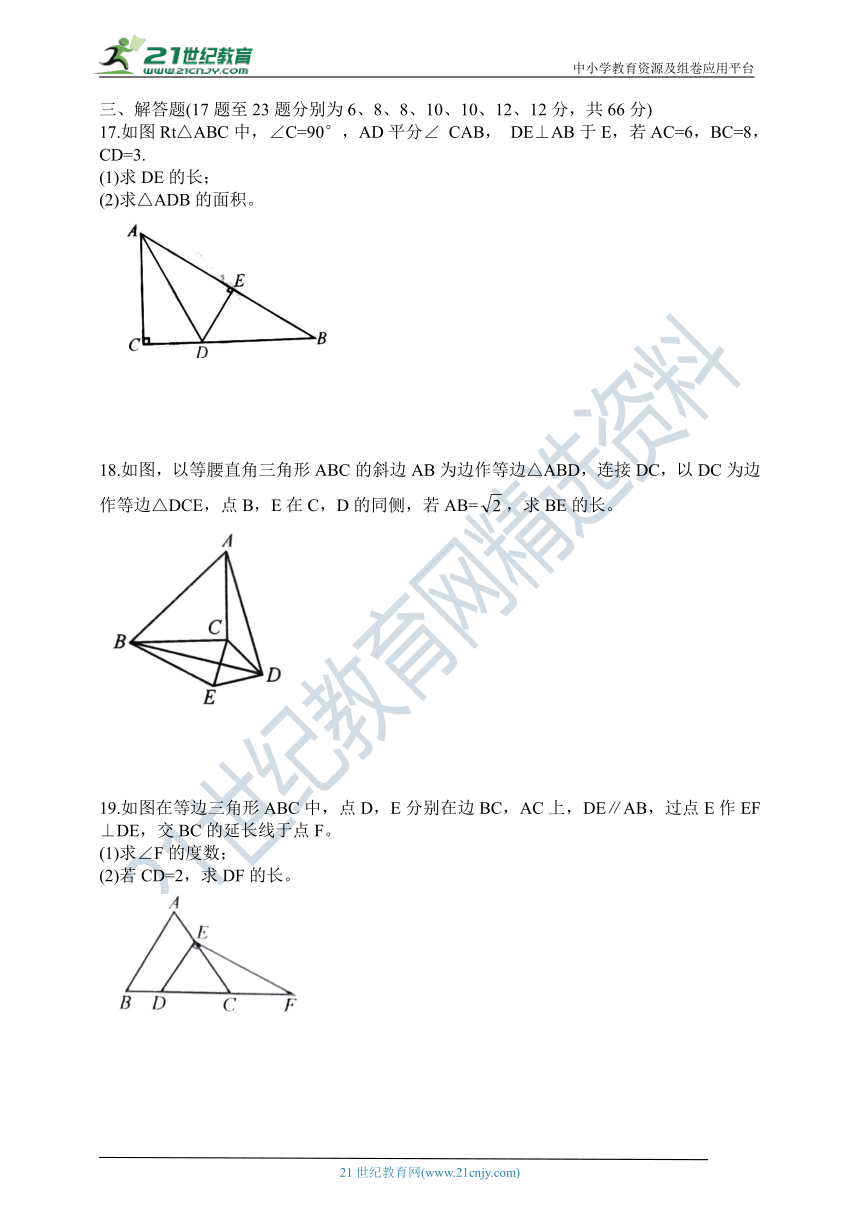
5.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为(
)。
A.2
B.
C.
D.
6.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB’C’,若AC=1,则图中阴影部分的面积为(
)。
A.
B.
C.
D.3
7.如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,AD=BC将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形则能拼出互不全等的四边形的个数是(
)。
A.1
B.2
C.3
D.4
8.如图在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于点D,E为AB上一点连接DE,则下列说法错误的是(
)。
A.∠CAD=30°
B.
AD=BD
C.
BD=2CD
D
CD=ED
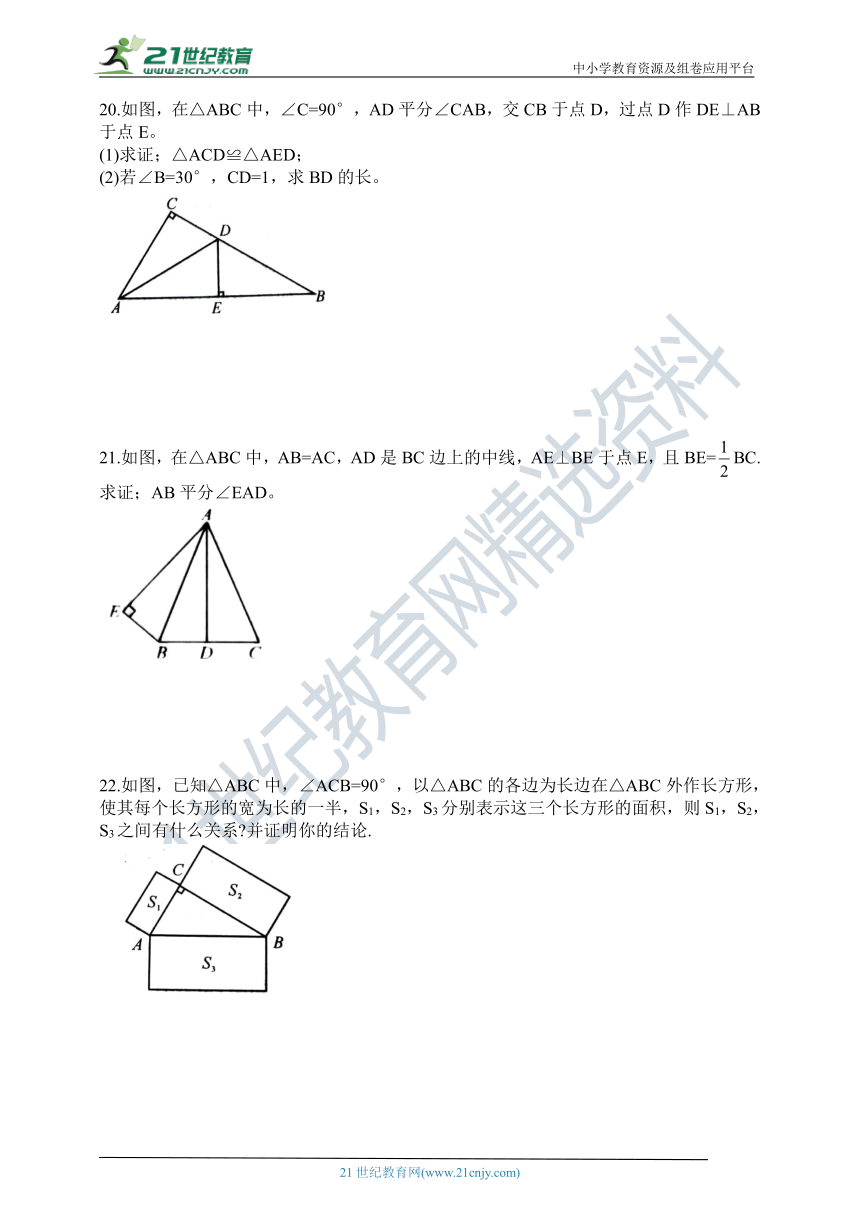
9.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,如果∠A=30°,AE=6cm,那么CE等于(
)。
A.cm
B.2cm
C.3cm
D.4cm
10.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=(
)。
A.3
B.4
C.5
D.6
二、填空题(每小题4分,共24分)
1l如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80m,那么点B离水平面的高度BC的长为
cm.
12.将一个有45角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为
cm.
13.如图,长方形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则AE两点间的距离为
.
14.如图,两建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为
m.
15.如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OAA2,以OA2为直角边作等腰R△OA2A3,,...则OA4的长度为
.
16.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.如图Rt△ABC中,∠C=90°,AD平分∠
CAB,
DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积。
18.如图,以等腰直角三角形ABC的斜边AB为边作等边△ABD,连接DC,以DC为边作等边△DCE,点B,E在C,D的同侧,若AB=,求BE的长。
19.如图在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F。
(1)求∠F的度数;
(2)若CD=2,求DF的长。
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E。
(1)求证;△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
21.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=BC.求证;AB平分∠EAD。
22.如图,已知△ABC中,∠ACB=90°,以△ABC的各边为长边在△ABC外作长方形,使其每个长方形的宽为长的一半,S1,S2,S3分别表示这三个长方形的面积,则S1,S2,S3之间有什么关系?并证明你的结论.
23.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.
(1)求证;CE=CF;
(2)求证;∠AEB=75°;
(3)求正方形ABCD的面积.
第2章
特殊三角形
(2.5-2.8)
参考答案
一、选择题
1.B
2.A
3.B
4.B
5.D
6.B
7.D
8.D
9.C
10.C
二、填空题
11.40
12cm
13.2
14.
15.4
16.8
三、解答题
17.(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
在△ACD和△AED中:∠C=∠AED=90°,∠CAD=∠DAE,AD=DA,
∴△ACD≌△AED,∴CD=DE,∵CD=3,∴DE=3;
(2)在Rt△ABC中,由勾股定理得;AB=,
∴△ADB的面积为(解法不唯一)
18.解;因为△ABD和△CDE都是等边三角形,
所以AD=BD,CD=DE,∠ADB=∠CDE=60°.
所以∠ADB-∠CDB=∠CDE-∠CDB,即∠ADC=∠BDE。
在△ADC和△BDE中,因为AD=BD,CD=DE,∠ADC=∠BDE,
所以△ADC≌△BDE,所以AC=BE.
在等腰Rt△ABC中,因为AB=√2,所以AC=BC=1,故BE=1.
19(1)∵△ABC是等边三角形,∴∠B=60°,
∵DE∥AB,∠EDC=∠B=60°,∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形.∴ED=DC=2,
∵∠DEF=90°,∠F=30°,∴DF=2DE=4
20.(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴∠CAD=∠DAE,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中:∠CAD=∠DAE,∠C=∠DEA=90°,AD=AD。
∴Rt△ACD≌Rt△AED(AAS)
(2)∵DC=DE=1,DE⊥AB,∴∠DEB=90°,
∵∠B=30°,∴BD=2DE=2
21.证明:∵AB=AC,AD是BC边上的中线,
BD=BC,AD⊥BC,∵BE=BC,∴BD=BE,
∵AE⊥BE,∴AB平分∠EAD.
22.S1+S2=S3.证略
23.解;(1)∵四边形ABCD是正方形,∴AB=AD,
∵△AEF是等边三角形,∴AE=AF,
在Rt△ABE和Rt△ADF中;AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,∴BC-BE=CD-DF,∴CE=CF.
(2)∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,
∴∠AEB=75°.
(3)如图,连接AC交EF于点G,连接BD.
∵四边形ABCD是正方形.∴∠BAG=∠DAG=∠ECG=∠FCG=45°,且BD=AC.
又∵∠BAE=∠DAF,∴∠BAG-∠BAE=∠DAG-∠DAF,即∠EAG=∠FAG,
又∵△AEF是边长为2的等边三角形,∴AC⊥EF,EG=FG=×2=1.
∴CG=EG=1,AG=,
∴AC=AG+CG=+1,∴BD=AC=+1,
∴S正方形ABCD=AC·BD=×(+1)2=×(4+2)=2+,
故正方形ABCD的面积为2+.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第2章
特殊三角形
2.5-2.8
同步测试
(含答案)
一、选择题(每小题3分,共30分)
1.如图,在Rt△ADB中,∠D=90°,C为AD上一点,则x可能是(
)。
A.10°
B.20°
C.30°
D.40°
2.将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CED’=60°,则∠AED的大小是(
)。
A.60°
B.50°
C.75°
D.55°
3.如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为(
)。
A.a
B.
2a
C.a
D.
a
4.如图,CD是Rt△ABC斜边上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
A.25°
B.30°
C.45°
D.60°
5.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为(
)。
A.2
B.
C.
D.
6.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB’C’,若AC=1,则图中阴影部分的面积为(
)。
A.
B.
C.
D.3
7.如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,AD=BC将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形则能拼出互不全等的四边形的个数是(
)。
A.1
B.2
C.3
D.4
8.如图在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于点D,E为AB上一点连接DE,则下列说法错误的是(
)。
A.∠CAD=30°
B.
AD=BD
C.
BD=2CD
D
CD=ED
9.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D,如果∠A=30°,AE=6cm,那么CE等于(
)。
A.cm
B.2cm
C.3cm
D.4cm
10.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=(
)。
A.3
B.4
C.5
D.6
二、填空题(每小题4分,共24分)
1l如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80m,那么点B离水平面的高度BC的长为
cm.
12.将一个有45角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为
cm.
13.如图,长方形纸片ABCD,AB=2,∠ADB=30°,沿对角线BD折叠(使△ABD和△EBD落在同一平面内),则AE两点间的距离为
.
14.如图,两建筑物AB和CD的水平距离为30m,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为
m.
15.如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OAA2,以OA2为直角边作等腰R△OA2A3,,...则OA4的长度为
.
16.如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE=
.
三、解答题(17题至23题分别为6、8、8、10、10、12、12分,共66分)
17.如图Rt△ABC中,∠C=90°,AD平分∠
CAB,
DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积。
18.如图,以等腰直角三角形ABC的斜边AB为边作等边△ABD,连接DC,以DC为边作等边△DCE,点B,E在C,D的同侧,若AB=,求BE的长。
19.如图在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F。
(1)求∠F的度数;
(2)若CD=2,求DF的长。
20.如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E。
(1)求证;△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
21.如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=BC.求证;AB平分∠EAD。
22.如图,已知△ABC中,∠ACB=90°,以△ABC的各边为长边在△ABC外作长方形,使其每个长方形的宽为长的一半,S1,S2,S3分别表示这三个长方形的面积,则S1,S2,S3之间有什么关系?并证明你的结论.
23.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.
(1)求证;CE=CF;
(2)求证;∠AEB=75°;
(3)求正方形ABCD的面积.
第2章
特殊三角形
(2.5-2.8)
参考答案
一、选择题
1.B
2.A
3.B
4.B
5.D
6.B
7.D
8.D
9.C
10.C
二、填空题
11.40
12cm
13.2
14.
15.4
16.8
三、解答题
17.(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
在△ACD和△AED中:∠C=∠AED=90°,∠CAD=∠DAE,AD=DA,
∴△ACD≌△AED,∴CD=DE,∵CD=3,∴DE=3;
(2)在Rt△ABC中,由勾股定理得;AB=,
∴△ADB的面积为(解法不唯一)
18.解;因为△ABD和△CDE都是等边三角形,
所以AD=BD,CD=DE,∠ADB=∠CDE=60°.
所以∠ADB-∠CDB=∠CDE-∠CDB,即∠ADC=∠BDE。
在△ADC和△BDE中,因为AD=BD,CD=DE,∠ADC=∠BDE,
所以△ADC≌△BDE,所以AC=BE.
在等腰Rt△ABC中,因为AB=√2,所以AC=BC=1,故BE=1.
19(1)∵△ABC是等边三角形,∴∠B=60°,
∵DE∥AB,∠EDC=∠B=60°,∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°;
(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形.∴ED=DC=2,
∵∠DEF=90°,∠F=30°,∴DF=2DE=4
20.(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴∠CAD=∠DAE,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中:∠CAD=∠DAE,∠C=∠DEA=90°,AD=AD。
∴Rt△ACD≌Rt△AED(AAS)
(2)∵DC=DE=1,DE⊥AB,∴∠DEB=90°,
∵∠B=30°,∴BD=2DE=2
21.证明:∵AB=AC,AD是BC边上的中线,
BD=BC,AD⊥BC,∵BE=BC,∴BD=BE,
∵AE⊥BE,∴AB平分∠EAD.
22.S1+S2=S3.证略
23.解;(1)∵四边形ABCD是正方形,∴AB=AD,
∵△AEF是等边三角形,∴AE=AF,
在Rt△ABE和Rt△ADF中;AB=AD,AE=AF,∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,∴BC-BE=CD-DF,∴CE=CF.
(2)∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,
∴∠AEB=75°.
(3)如图,连接AC交EF于点G,连接BD.
∵四边形ABCD是正方形.∴∠BAG=∠DAG=∠ECG=∠FCG=45°,且BD=AC.
又∵∠BAE=∠DAF,∴∠BAG-∠BAE=∠DAG-∠DAF,即∠EAG=∠FAG,
又∵△AEF是边长为2的等边三角形,∴AC⊥EF,EG=FG=×2=1.
∴CG=EG=1,AG=,
∴AC=AG+CG=+1,∴BD=AC=+1,
∴S正方形ABCD=AC·BD=×(+1)2=×(4+2)=2+,
故正方形ABCD的面积为2+.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
