2.2二次函数的图象（第2课时）

(共18张PPT)
课程标准浙教版实验教科书
九年级 上 册
知识回顾:
二次函数y=ax 的图象及其特点？
1、顶点坐标？
（0，0）
2、对称轴？
y轴（直线x=0）
3、图象具有以下特点：
一般地，二次函数y=ax （ a≠0 ）的图象是一条抛物线，
当a>0 时，抛物线开口向上，顶点是抛物线上的最低点，
抛物线在x轴的上方（除顶点外）；
当a<0 时，抛物线开口向下，顶点是抛物线上的最高点，
抛物线在x轴的下方（除顶点外）。
完成书上32页合作学习
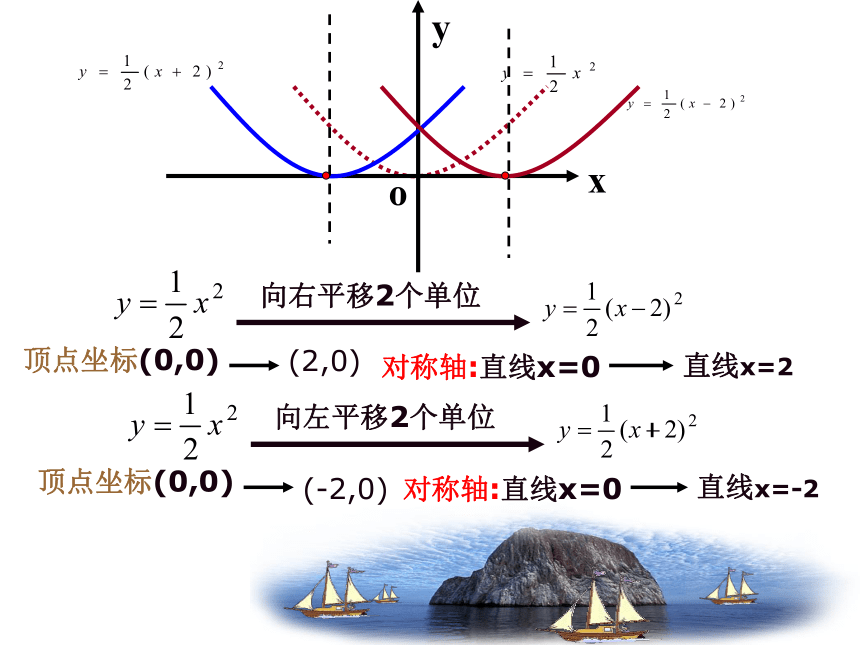
向右平移2个单位
顶点坐标(0,0)
(2,0)
对称轴:直线x=0
直线x=2
向左平移2个单位
顶点坐标(0,0)
(-2,0)
对称轴:直线x=0
直线x=-2
x
y
o
例
对于二次函数
请回答下列问题：
1、把函数 的图象作怎样的平移
变换，就能得到函数 的图象。
2、说出函数 的图象的顶点坐标
和对称轴。
二次函数y=a(x+ m)2的图象和性质.
当m>0时,向左平移
当m<0时,向右平移
a＞0时，开口_____, 最 ____ 点是顶点; a＜0时，开口_____, 最 ____ 点是顶点;
对称轴是 _________， 顶点坐标是 ______。
y=ax2
y=a(x+ m)2的图象
y=a(x+ m)2
向上
低
向下
高
直线x=-m
(-m，0)
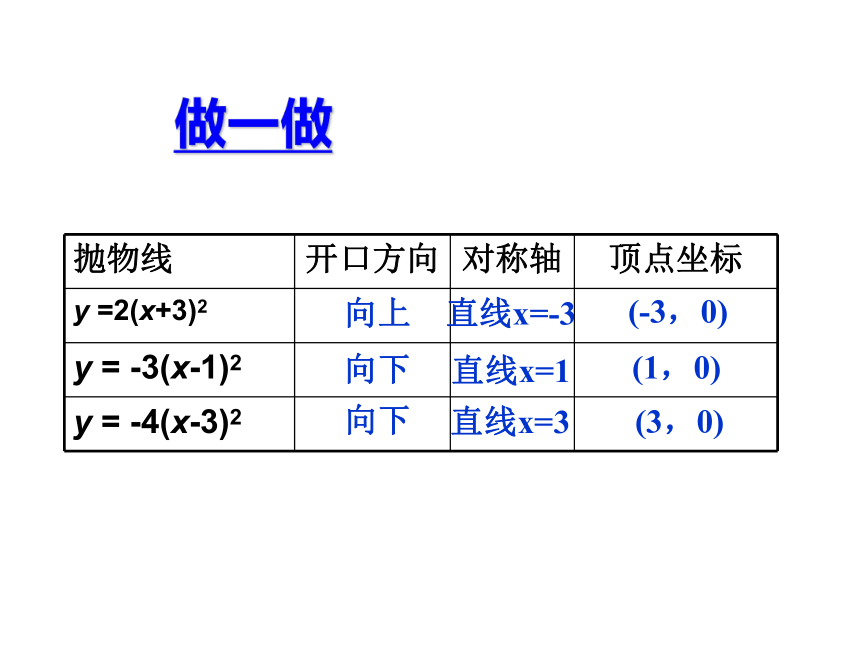
做一做
抛物线 开口方向 对称轴 顶点坐标
y =2(x+3)2
y = -3(x-1)2
y = -4(x-3)2
向上
直线x=-3
(-3，0)
向下
直线x=1
(1，0)
向下
直线x=3
(3，0)
动手实践
用描点法在同一直角坐标系中画出函数
与 的图象 .
由函数 的图象经过怎样平移得到函数
的图象
合作学习
先向左平移2个单位，再向上平移3个单位或先向上平移3个单位，再向左平移2个单位。
讨论归纳:
y=a(x+m)2+k的图象：
对称轴是 _________，顶点坐标是 _______。
直线x=-m
(-m, k)
当k>0时,向上平移
当k<0时,向下平移
y=a(x+m)2
y=a(x+ m)2+k
当m>0时,向左平移
当m<0时,向右平移
y=ax2
y=a(x+ m)2
m左加右减 k上加下减
一般地，平移二次函数y=ax2的图象就可得到二次函数y=a(x+m)2+k的图象。因此，二次函数y=a(x+m)2+k的形状、对称轴、顶点坐标和开口方向与a、m、k的值有关。
1、指出下列二次函数的开口方向、对称轴和顶点坐标：
课内练习:
填空：
1、由抛物线y=2x 向 平移 个单位,
再向 平移 个单位可得到y= 2(x +1)2 –3。
2、函数y= 3(x - 2)2 + 的图象。
可以由抛物线 向 平移 个单位，
再向 平移 个单位而得到的。
做一做:
1、 如果抛物线 的顶点坐标
是（-1，5）则
它的对称轴是
２、 如果一条抛物线的形状与
的形状相同，且顶点坐标是（４，-２）
求该函数解析式.
这节课你有什么收获和体会？
3
4
5、已知二次函数
的图象如图所示，则函数
的图象只可能是（ ）