3.3圆心角(1)
图片预览





文档简介
(共33张PPT)
直径CD⊥AB
O
C
D
A
B
E
圆的轴对称性
垂径定理及逆定理
⌒
⌒
⌒
⌒
义务教育课程标准实验教科
浙江版《数学》九年级上册
茶杯的盖子做成圆
形有什么好处呢?
圆绕圆心旋转任意一个角度,都能够与原来的圆重合。
圆的旋转不变性:
圆是中心对称图形,圆心是它的对称中心。
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
图1
则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。
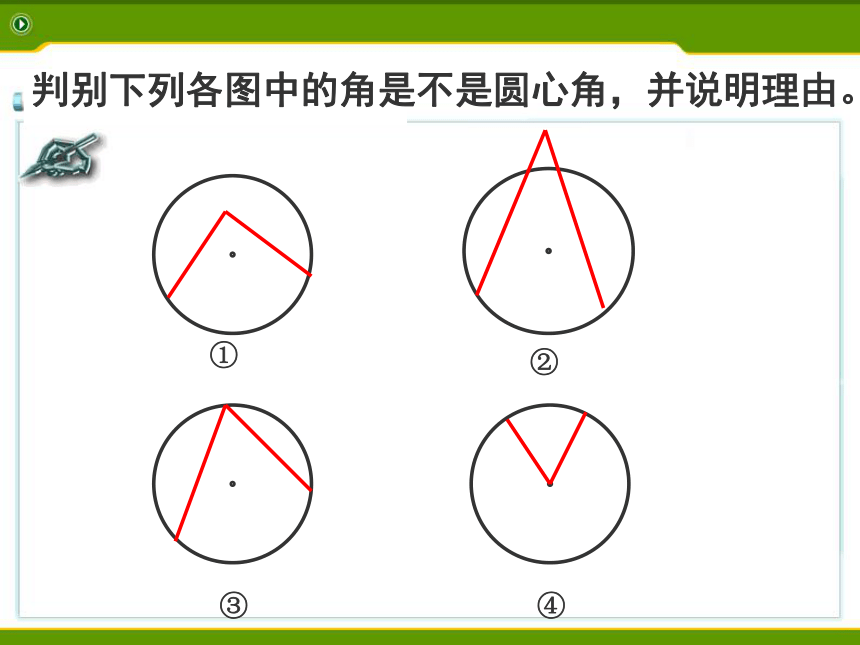
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
C
D
o
A
B
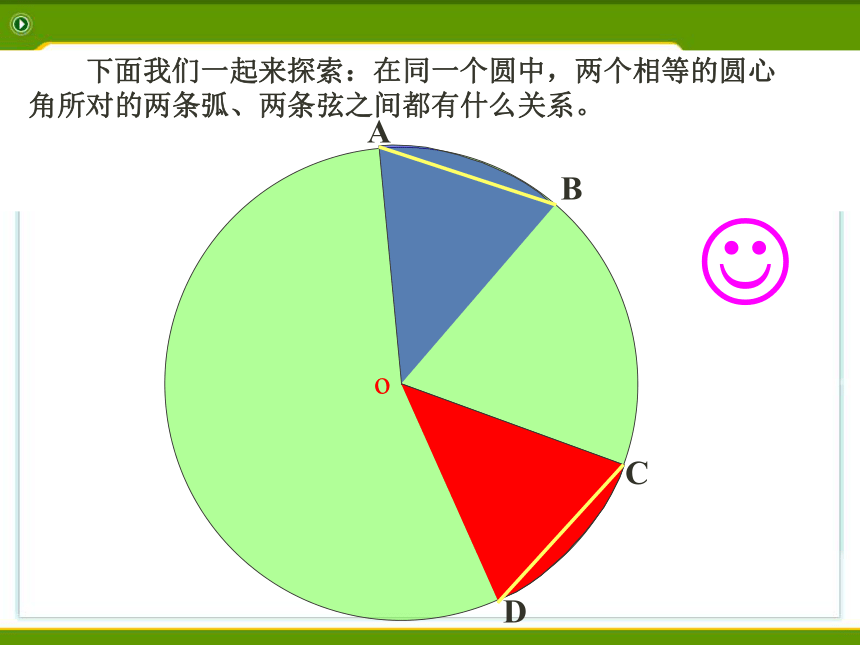
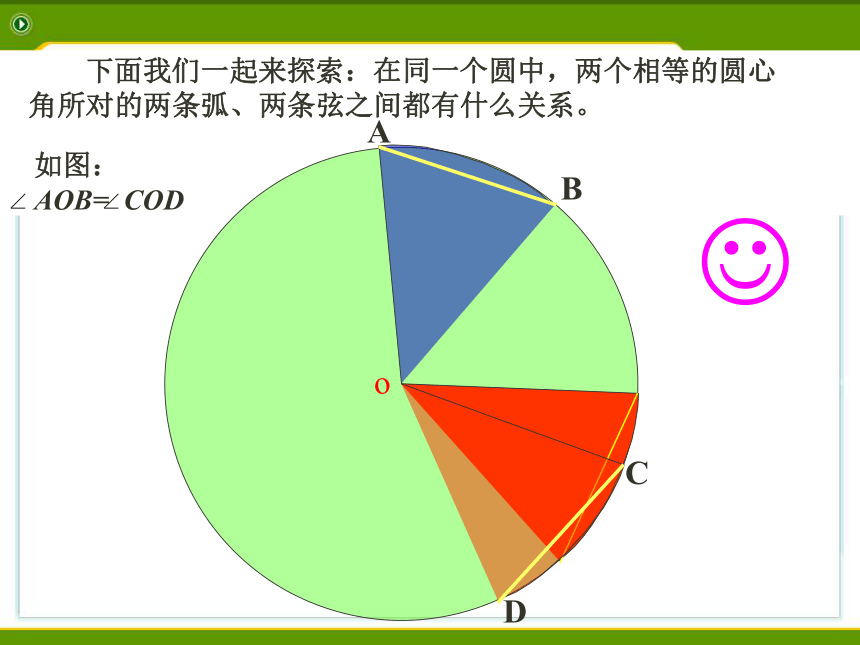
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
C
D
o
A
B
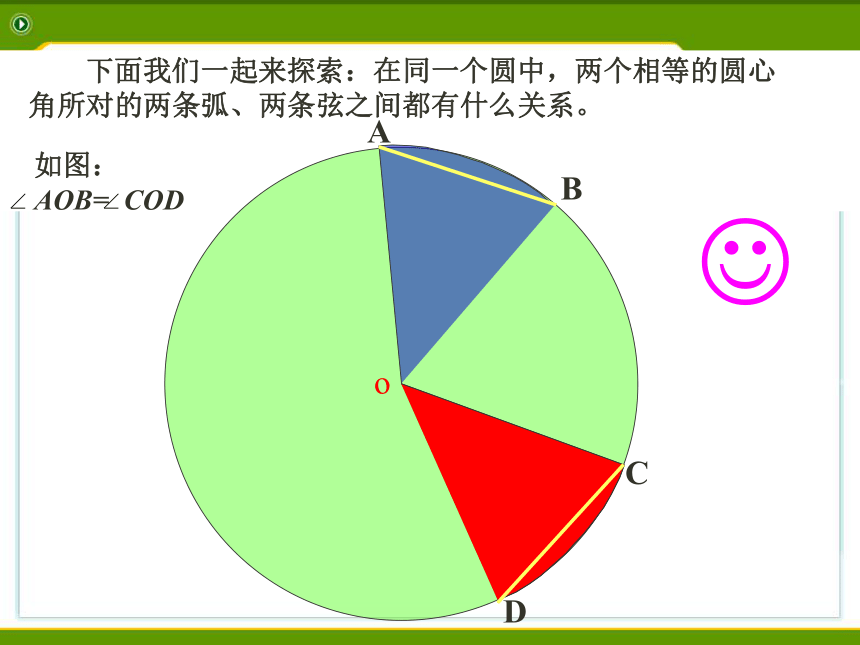
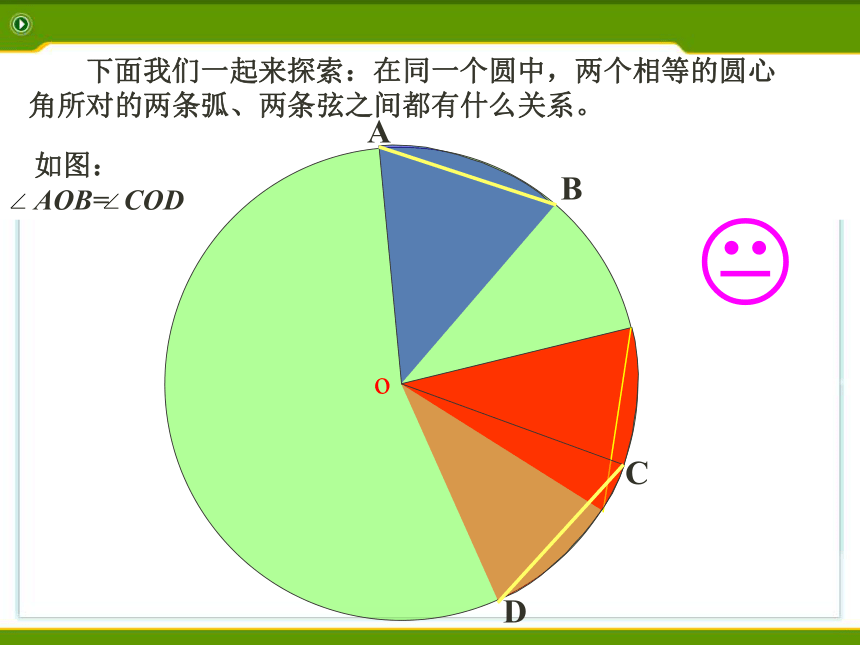
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
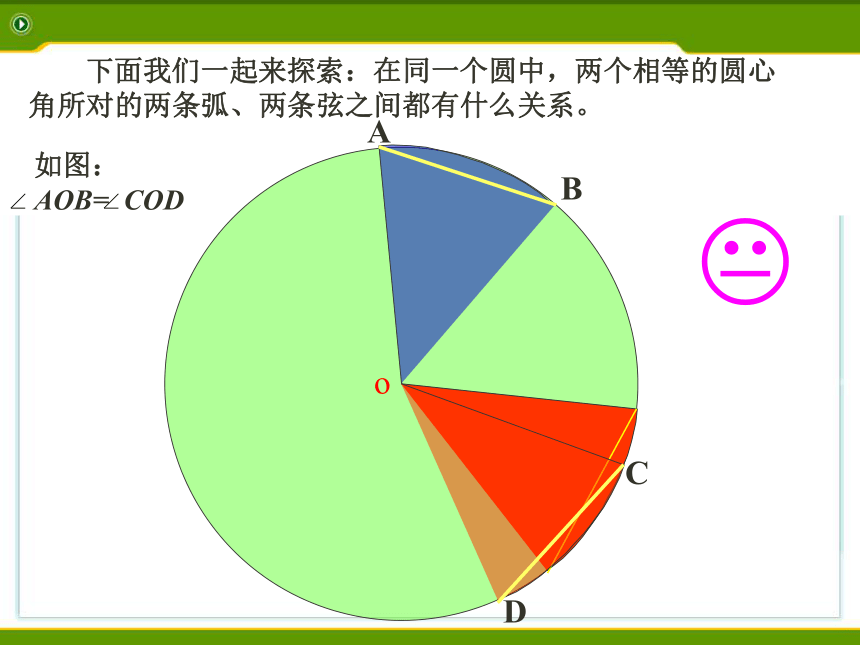
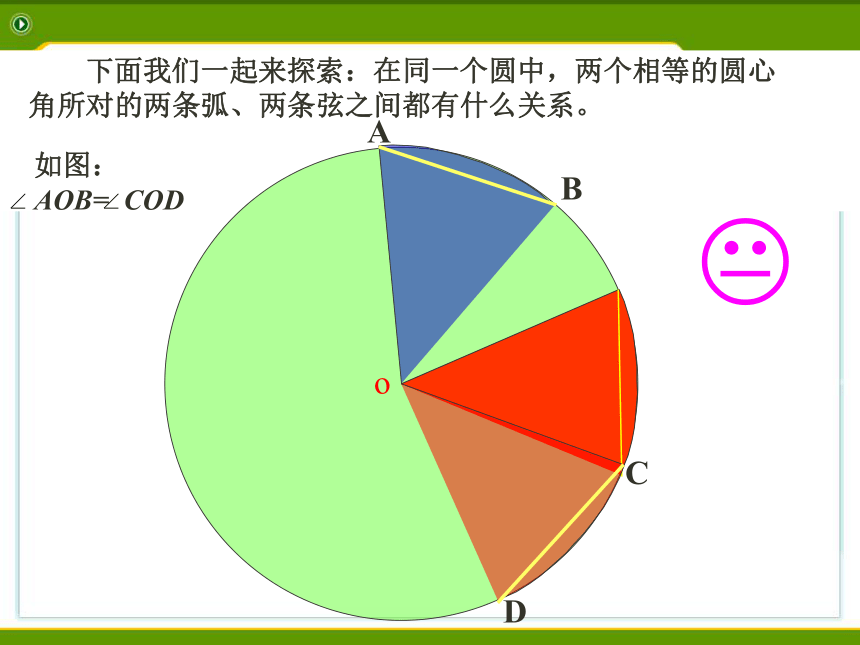
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
A
B
C
D
o
圆心角定理:
弦AB和弦CD对应的弦心距什么关系?
相等的圆心角所对的弧相等,
所对的弦相等
所对弦的弦心距相等
在同圆或等圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD AB=CD(圆心角定理)
A
B
C
D
AB=CD吗?
弧AB与弧CD呢?
O
A
B
C
D
o
圆心角定理:
相等的圆心角所对的弧相等,
所对的弦相等
所对弦的弦心距相等
在同圆或等圆中,
E
F
1.相等的圆心角所对的弧相等。( )
2.已知:如图, ∠ 1= ∠ 2,求证:AC=BD
2
A
B
C
D
1
证明:∵ ∠ 1= ∠ 2
∴DC=BA(圆心角定理)
∴ DC+BC= BA+BC
即BD=AC
O
例1:用直尺和圆规把⊙O四等分.
O
作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
你能将任意一个
圆八等分吗?
六
A
B
C
D
例1:用直尺和圆规把⊙O四等分.
O
作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
若要把圆作n等分,
关键是先作什么?
A
B
C
D
我们把1 的圆心角所对的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
A
O
B
1.如图一,已知∠AOC=135°,
则CB的度数为
—
O
A
B
C
图(一)
2.如图,∵∠AOC=∠BOD
∴AC =BD
问:以上说法对不对?为什么?
那么,怎样情况下, AC =BD?
3.下列说法正确的是( )
A.相等的圆心角所对的弧相等。
B.相等的圆心角所对的弦相等。
C.度数相等的两条弧相等。
D.相等的圆心角所对的弧的度数相等。
D
A
B
C
D
O
4.已知如图,∠1=∠2
求证: AC =BD
A
B
D
C
1
2
O
大胆说出你的见解
通过本节的学习,你对圆有哪些新的认识?
如图,C是圆0的直径AB上一点,过点C作弦DE,使CD=CO,若 AD的度数为30,求BE的度数。
。
A
B
C
D
O
E
已知:如图, AB为⊙O的弦,E、F是AB上的两点,且AE=BF,OE、OF分别交AB于点C、D
求证:AC=BD
直径CD⊥AB
O
C
D
A
B
E
圆的轴对称性
垂径定理及逆定理
⌒
⌒
⌒
⌒
义务教育课程标准实验教科
浙江版《数学》九年级上册
茶杯的盖子做成圆
形有什么好处呢?
圆绕圆心旋转任意一个角度,都能够与原来的圆重合。
圆的旋转不变性:
圆是中心对称图形,圆心是它的对称中心。
圆心角 所对
的弧为 AB,
过点O作弦AB的垂线, 垂足
为M,
O
A
B
M
顶点在圆心的角,叫圆心角,
如 ,
所对的弦为AB;
图1
则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。
判别下列各图中的角是不是圆心角,并说明理由。
①
②
③
④
C
D
o
A
B
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
C
D
o
A
B
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
如图: AOB= COD
o
A
B
C
D
下面我们一起来探索:在同一个圆中,两个相等的圆心角所对的两条弧、两条弦之间都有什么关系。
A
B
C
D
o
圆心角定理:
弦AB和弦CD对应的弦心距什么关系?
相等的圆心角所对的弧相等,
所对的弦相等
所对弦的弦心距相等
在同圆或等圆中,
E
F
∵ ∠ AOB= ∠ COD
∴AB=CD AB=CD(圆心角定理)
A
B
C
D
AB=CD吗?
弧AB与弧CD呢?
O
A
B
C
D
o
圆心角定理:
相等的圆心角所对的弧相等,
所对的弦相等
所对弦的弦心距相等
在同圆或等圆中,
E
F
1.相等的圆心角所对的弧相等。( )
2.已知:如图, ∠ 1= ∠ 2,求证:AC=BD
2
A
B
C
D
1
证明:∵ ∠ 1= ∠ 2
∴DC=BA(圆心角定理)
∴ DC+BC= BA+BC
即BD=AC
O
例1:用直尺和圆规把⊙O四等分.
O
作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
你能将任意一个
圆八等分吗?
六
A
B
C
D
例1:用直尺和圆规把⊙O四等分.
O
作法:1、作⊙O的直径AB。
2、过点O作CD⊥AB,交⊙O于
点C和点D。
点A,B,C,D就把⊙O四等分
若要把圆作n等分,
关键是先作什么?
A
B
C
D
我们把1 的圆心角所对的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
A
O
B
1.如图一,已知∠AOC=135°,
则CB的度数为
—
O
A
B
C
图(一)
2.如图,∵∠AOC=∠BOD
∴AC =BD
问:以上说法对不对?为什么?
那么,怎样情况下, AC =BD?
3.下列说法正确的是( )
A.相等的圆心角所对的弧相等。
B.相等的圆心角所对的弦相等。
C.度数相等的两条弧相等。
D.相等的圆心角所对的弧的度数相等。
D
A
B
C
D
O
4.已知如图,∠1=∠2
求证: AC =BD
A
B
D
C
1
2
O
大胆说出你的见解
通过本节的学习,你对圆有哪些新的认识?
如图,C是圆0的直径AB上一点,过点C作弦DE,使CD=CO,若 AD的度数为30,求BE的度数。
。
A
B
C
D
O
E
已知:如图, AB为⊙O的弦,E、F是AB上的两点,且AE=BF,OE、OF分别交AB于点C、D
求证:AC=BD
同课章节目录
