求二次函数的解析式

(共23张PPT)
二次函数的三种解析式
1.一般式y=ax2+bx+c(a≠0）
2.双根式y=a(x-x1)(x-x2)
3.顶点式y=a(x-h)2+k
y=ax2+bx+c(a≠0）一般式
a , b同号
a , b异号
C＞0
C＜0
C=0 经过原点
x
y
o
C
x
y
o
C
x
y
o
C
x
y
o
C
x
y
o
C
顶点坐标
对 称 轴
与y轴正半轴相交
与y轴负半轴相交
对称轴在y轴的左侧
对称轴在y轴的右侧
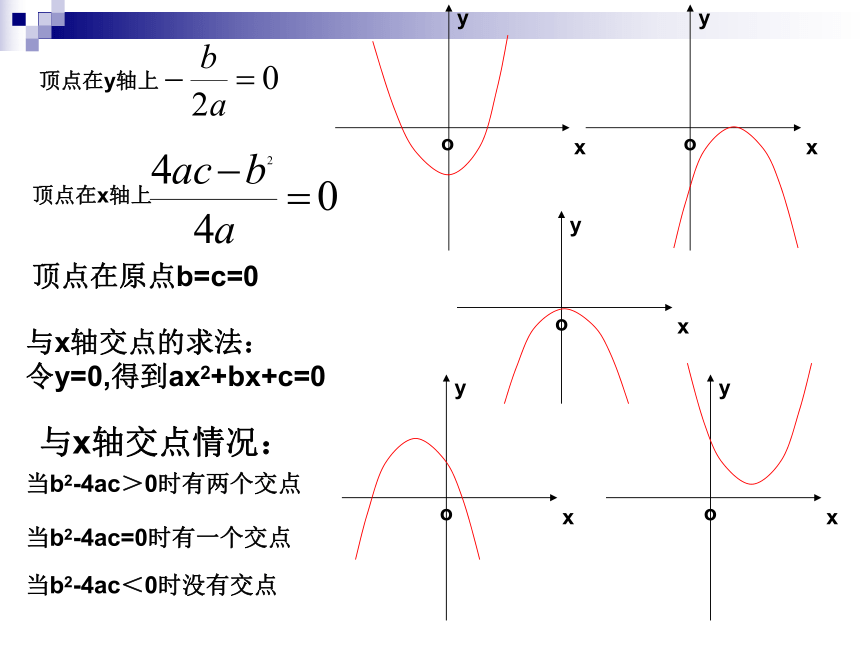
与x轴交点的求法：
令y=0,得到ax2+bx+c=0
与x轴交点情况：
当b2-4ac＞0时有两个交点
当b2-4ac=0时有一个交点
当b2-4ac＜0时没有交点
顶点在y轴上
顶点在x轴上
x
y
o
x
y
o
x
y
o
顶点在原点b=c=0
x
y
o
x
y
o
与y轴交点的求法：令x=0,得到y=c 即（0，c）
与y轴始终有一个交点（0，c）
如果y=ax2+bx+c的图象与x轴的交点为A(x1,0),B(x2,0);
那么AB=|x1-x2|=
x
y
o
C
x1
x2
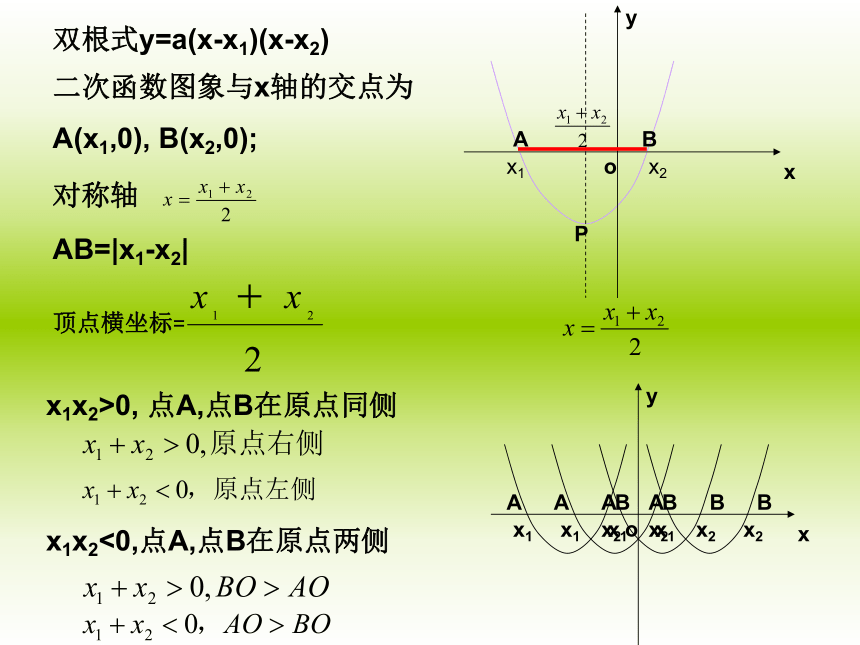
双根式y=a(x-x1)(x-x2)
对称轴
二次函数图象与x轴的交点为
A(x1,0), B(x2,0);
AB=|x1-x2|
顶点横坐标=
x
y
o
x2
x1
P
A
B
x1x2>0, 点A,点B在原点同侧
x1x2<0,点A,点B在原点两侧
x
y
o
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
A
B
x1
x2
顶点式 y=a(x-h)2+k
顶点坐标(h , k)
对称轴 x=h
当a>0, x=h时,y有最小值为k
x当k=0时顶点在x轴上
k
h
x
y
o
当a<0, x=h时,y有最大值为k
x>h表示在对称轴的右侧
当h=0时,顶点在y轴上；
x
y
o
h
k
k
h
h
x
y
o
h
-h
k
-k
(h, k)
若a>0, h>0, k>0
把y=ax2的图象向右平移h个单位得到
向左平移h个单位得到
向上平移k个单位得到
向下平移k个单位得到
向右平移h个单位并向上平移k个单位得到
y=a(x+h)2
y=ax2+k
y=ax2-k
y=a(x-h)2+k
y=a(x-h)2
( 1 )图象过A(0，1) 、B（1，2）、C（2，-1）三点
一: 已知抛物线y=ax2+bx+c满足下列条件,求函数的解析式.
（1）解：设抛物线的解析式为y=ax2+bx+c
∵图象过A(0，1) 、B（1，2）、C（2，-1）三点
∴
∴
∴y= -2x2+3x+1
x
y
o
解：∵A(1，0)，对称轴为x=2
∴抛物线与x轴另一个交点C应为（3，0）
∴设其解析式为y=a(x-1)(x-3)
∵B（0，-3）
∴-3=a（0-1）（0-3）
∴a= -1
∴y= -(x-1)(x-3)
（2）图象经过A（1，0）、B（0，-3），且对称轴是直线x=2
1
A
B
-3
C
3
2
（3）图象顶点是（-2，3），且经过点（-1，5）
解：∵图象顶点是（-2，3）
∴设其解析式为y=a（x+2）2+3
∵经过点（-1，5）
∴5=a（-1+2）2+3
∴a=2
∴y=2（x+2）2+3
（4）图象和x轴交于（-2，0）、（4，0）两点且顶点为（1，-9/2）
解：由于题中告诉了图象与x轴的交点坐标，又告诉了顶点坐标，所以既可以用双根式又可以用顶点式来设其解析式
设双根式为：y=a(x+2)(x-4)
∴-9/2=a(1+2)(1-4)
∵顶点为（1，-9/2）
∴a= -1/2
∴y= -1/2(x+2)(x-4)
（5）图象顶点是M（1，16）且与x轴交于两点，已知两交点相距8个单位。
解： ∵顶点M坐标为（1，16），对称轴为x=1，又交点A、B关于直线x=1对称，AB=8
∴A（-3，0）、B（5，0）
∴此函数解析式可设为
y=a（x-1）2+16
或y=a（x+3）（x-5）
x
y
o
1
16
A
B
- 3
5
二:求满足下列条件的抛物线的解析式
(1)经过点A（2，4），B（-1，0）且在x轴上截得的线段长为2
解： ∵B（-1，0）且在x轴上截得的线段长为2
∴抛物线与x轴的另一个交点坐标为C（-3，0）或C’（1，0）
∴设抛物线的解析式为y=a（x- x1）（x- x2）
①当抛物线经过B、C三点时，解析式为y=a（x+1）（x+3）
又∵抛物线经过A（2，4）
∴4=a（2+1）（2+3）
②当抛物线经过B、C’ 三点时，解析式为y=a（x+1）（x-1）
x
y
o
B
-1
- 3
1
C
C’
∴a=
∴y= （x+1）（x+3）
(2)交x轴于A（x1，0），B（x2，0），顶点为P（1，-4），且x12+x22=10
解： ∵ =1
∴ =2
∵ x12+x22=10
∴x1= -1 ; x2=3
∴ A（-1，0），B（3，0）
∴抛物线的解析式为y=a（x+ 1）（x- 3）
又∵抛物线的顶点为P （1，-4）
∴-4=a（1+1）（1- 3）
∴a=1
∴y = （x+ 1）（x- 3）
x
y
o
1
-4
A
B
-1
3
P
x
y
o
1
-3
-2
三: 二次函数y=ax2+bx+c的图象如图所示
对称轴x=_____
顶点坐标:______
当x=_____时,y有最_____值是____
函数值y<0时,对应x的取值范围是_______
函数值y>0时,对应x的取值范围是_______
函数值y=0时,对应x的取值范围是_______
当x_______时,y随x的增大而增大.
-1
(-1,-2)
-1
小
-2
-3x<-3或x>1
-3或1
>-1
四 :已知二次函数
y=ax2+bx+c的图象如图所
示,下列结论①a+ b + c<0
②a – b + c>0 ③abc>0 ④
b=2a。其中正确的结论的
个数是（ ）
A 1个 B 2个 C 3个 D 4个
x
y
O
-1
1
m
n
D
课堂小结：
1. 抛物线的三种解析式？
3. 各种解析式对称轴、顶点坐标求法？
2. 如何选择这三种解析式求抛物线的解析式？
4. 二次函数的最值的求法？
5. 抛物线的平移规律？
6. 抛物线与x轴两交点距离的求法？