浙教版九年级数学上册期中复习——圆的基本性质学案(知识点+例题含解析)
文档属性
| 名称 | 浙教版九年级数学上册期中复习——圆的基本性质学案(知识点+例题含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 342.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 21:27:27 | ||
图片预览



文档简介
《圆的基本性质》章节复习
【要点梳理】
要点一、圆的定义、性质及与圆有关的角
1.圆的定义
(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.
(2)圆是到定点的距离等于定长的点的集合.
(3)不在同一条直线上的三个点确定一个圆.
要点诠释:
①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;
②圆是一条封闭曲线.
2.点与圆的位置关系
判定一个点P是否在⊙O上
设⊙O的半径为,OP=,则有
点P在⊙O
外; 点P在⊙O
上;点P在⊙O
内.
要点诠释:
点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.
3.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
定理2:平分弧的直径垂直平分弧所对的弦.
4.与圆有关的角
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
在同圆或者等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.
在同圆或者等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
5.
圆内接四边形
圆内接四边形的对角互补.
要点二、图形的旋转
在平面内,一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的角叫做旋转角.
图形经过旋转所得的图形和原图形全等.
对应点到旋转中心的距离相等.任何一对对应点与旋转中心连线所成的角度等于旋转的角度.
要点三、正多边形
各边相等,各内角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
要点四、弧长及扇形的面积
圆心角为、半径为R的弧长.
圆心角为,半径为R,弧长为的扇形的面积.
要点诠释:
(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,
即;
(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.
(3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;
(4)扇形两个面积公式之间的联系:.
【典型例题】
类型一、圆的基础知识
1.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点在数轴上运动,若过点P且与OA平行(或重合)的直线与⊙O有公共点,
设OP=x,则的取值范围是(
).
A.-1≤≤1
B.≤≤
C.0≤≤
D.>
【答案】C;
【解析】如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OA∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′=,
∴当过点P且与OA平行的直线与⊙O有公共点时,0≤OP≤,
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0≤OP≤.
【总结升华】本题考查了直线与圆的位置关系问题.关键是通过平移,确定直线与圆相切的情况,求出此时OP的值.
举一反三:
【变式】如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是( ).
A.-1≤x<0或0<x≤1
B.0<x≤1
C.-≤x<0或0<x≤
D.x>1
【答案】∵⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,
∴过点P′且与OB平行的直线与⊙O相切时,假设切点为D,
∴OD=DP′=1,
OP′=,
∴0<OP≤,
同理可得,当OP与x轴负半轴相交时,
-≤OP<0,
∴-≤OP<0,或0<OP≤.
故选C.
类型二、弧、弦、圆心角、圆周角的关系及垂径定理
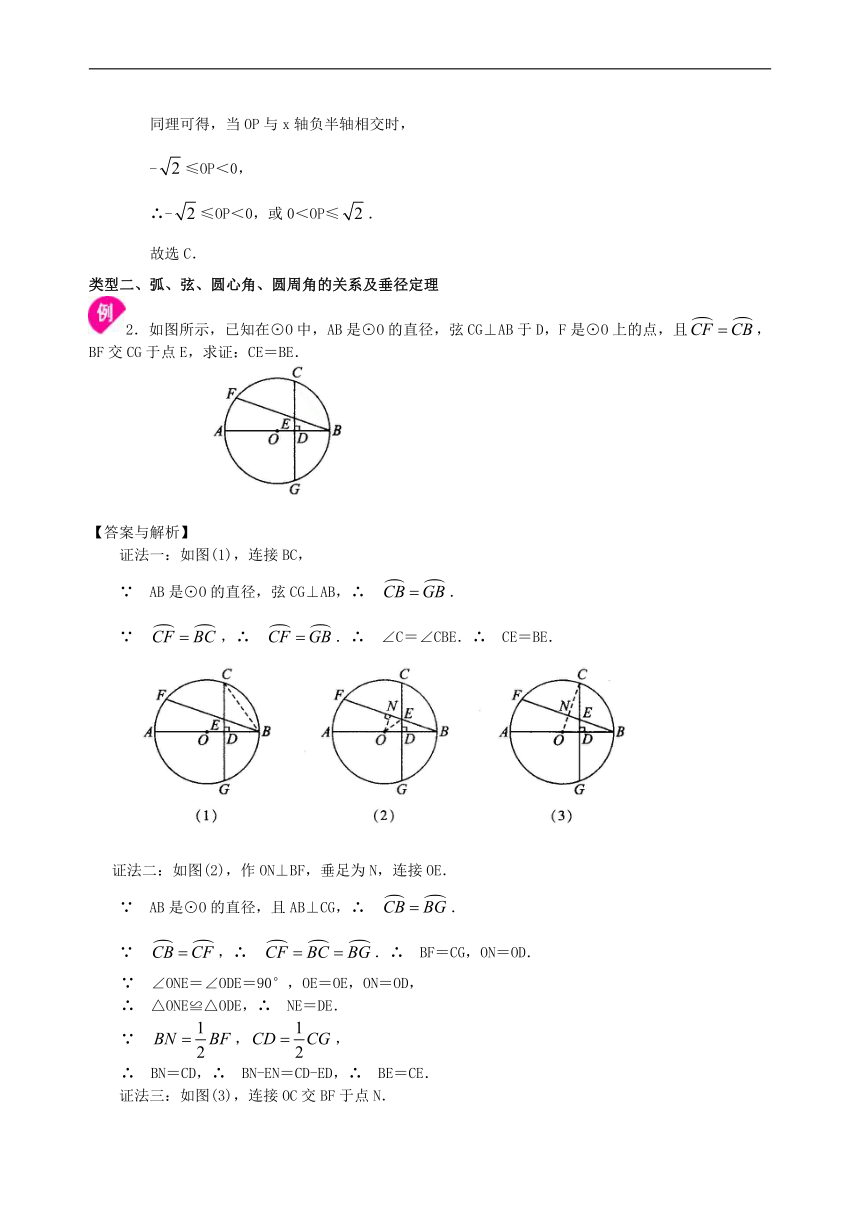
2.如图所示,已知在⊙O中,AB是⊙O的直径,弦CG⊥AB于D,F是⊙O上的点,且,BF交CG于点E,求证:CE=BE.
【答案与解析】
证法一:如图(1),连接BC,
∵
AB是⊙O的直径,弦CG⊥AB,∴
.
∵
,∴
.∴
∠C=∠CBE.∴
CE=BE.
证法二:如图(2),作ON⊥BF,垂足为N,连接OE.
∵
AB是⊙O的直径,且AB⊥CG,∴
.
∵
,∴
.∴
BF=CG,ON=OD.
∵
∠ONE=∠ODE=90°,OE=OE,ON=OD,
∴
△ONE≌△ODE,∴
NE=DE.
∵
,,
∴
BN=CD,∴
BN-EN=CD-ED,∴
BE=CE.
证法三:如图(3),连接OC交BF于点N.
∵
,∴
OC⊥BF.
∵
AB是⊙O的直径,CG⊥AB,
∵
,.∴
,.
∵
OC=OB,∴
OC-ON=OB-OD,即CN=BD.
又∠CNE=∠BDE=90°,∠CEN=∠BED,
∴
△CNE≌△BDE,∴
CE=BE.
【总结升华】上述各种证明方法,虽然思路各异,但都用到了垂径定理及其推论.在平时多进行一题多解、一题多证、一题多变的练习,这样不但能提高分析问题的能力,而且还是沟通知识体系、学习知识,使用知识的好方法.
举一反三:
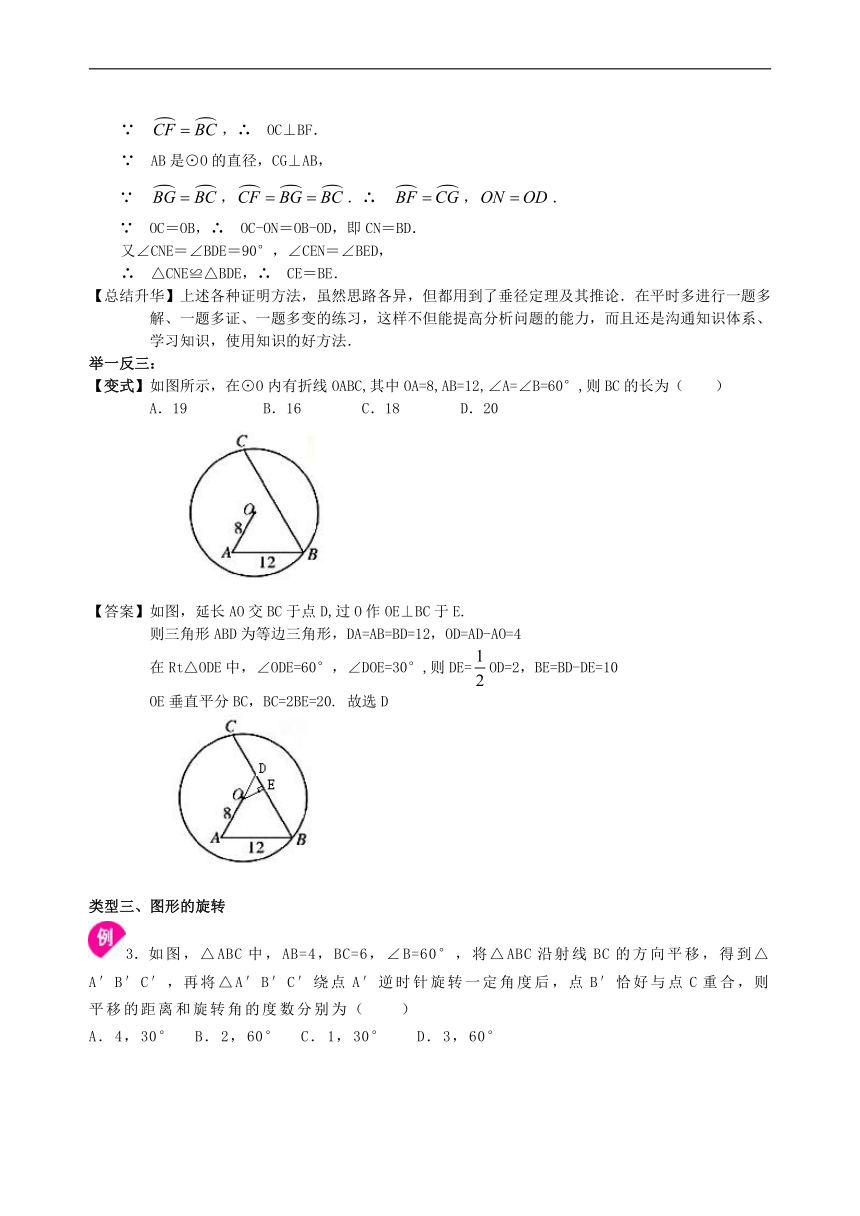
【变式】如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为(
)
A.19
B.16
C.18
D.20
【答案】如图,延长AO交BC于点D,过O作OE⊥BC于E.
则三角形ABD为等边三角形,DA=AB=BD=12,OD=AD-AO=4
在Rt△ODE中,∠ODE=60°,∠DOE=30°,则DE=OD=2,BE=BD-DE=10
OE垂直平分BC,BC=2BE=20.
故选D
类型三、图形的旋转
3.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
A.4,30°
B.2,60°
C.1,30°
D.3,60°
【思路点拨】利用旋转和平移的性质得出,∠A′B′C=60°,AB=A′B′=A′C=4,进而得出△A′B′C是等边三角形,即可得出BB′以及∠B′A′C的度数.
【答案】B;
解:∵∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,
∴∠A′B′C=60°,AB=A′B′=A′C=4,
∴△A′B′C是等边三角形,
∴B′C=4,∠B′A′C=60°,
∴BB′=6-4=2,
∴平移的距离和旋转角的度数分别为:2,60°.
【总结升华】此题主要考查了平移和旋转的性质以及等边三角形的判定等知识,得出△A′B′C是等边三角形是解题关键.
类型四、圆中有关的计算
4.(2016?绵阳)如图,AB为⊙O直径,C为⊙O上一点,点D是的中点,DE⊥AC于E,DF⊥AB于F.
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度.
【思路点拨】(1)先连接OD、AD,根据点D是的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;
(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.
【答案与解析】
解:(1)DE与⊙O相切.
证明:连接OD、AD,
∵点D是的中点,
∴=,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切.
(2)连接BC交OD于H,延长DF交⊙O于G,
由垂径定理可得:OH⊥BC,==,
∴=,
∴DG=BC,
∴弦心距OH=OF=4,
∵AB是直径,
∴BC⊥AC,
∴OH∥AC,
∴OH是△ABC的中位线,
∴AC=2OH=8.
【点评】本题主要考查了直线与圆的位置关系,在判定一条直线为圆的切线时,当已知条件中明确指出直线与圆有公共点时,通常连接过该公共点的半径,证明该半径垂直于这条直线.本题也可以根据△ODF与△ABC相似,求得AC的长.
举一反三:
【变式】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
【答案】解:(1)∵OF⊥AB,
∴∠BOF=90°,
∵∠B=30°,FO=2,
∴OB=6,AB=2OB=12,
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC=AB=6;
(2)∵由(1)可知,AB=12,
∴AO=6,即AC=AO,
在Rt△ACF和Rt△AOF中,
∴Rt△ACF≌Rt△AOF,
∴∠FAO=∠FAC=30°,
∴∠DOB=60°,
过点D作DG⊥AB于点G,
∵OD=6,∴DG=3,
∴S△ACF+S△OFD=S△AOD=×6×3=9,
即阴影部分的面积是9.
类型五、圆与其他知识的综合运用
5..
【答案与解析】
延长DB至点E,使BE=DC,连结AE
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°,AB=AC
∴∠ADB=∠ACB=60°
∵四边形ABDC是圆内接四边形
∴∠ABE=∠ACD
在△AEB和△ADC中,
∴△AEB≌△ADC
∴AE=AD
∵∠ADB=60°
∴△AED是等边三角形
∴AD=DE=DB+BE
∵BE=DC
∴DB+DC=DA.
【总结升华】由已知条件,等边△ABC可得60°角,根据圆的性质,可得∠ADB=60°,利用截长补短的方法可得一个新的等边三角形,再证两个三角形全等,从而转移线段DC.
本例也可以用其他方法证明.如:
(1)延长DC至F,使CF=BD,连结AF,再证△ACF≌△ABD,得出AD=DF,从而DB+CD=DA.
(2)在DA上截取DG=DC,连结CG,再证△BDC≌△AGC,得出BD=AG,从而DB+CD=DA.
6.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是(
).
A.
3
B.
6
C.
5
D.
4
【答案】B;
【解析】阴影部分的面积
=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积
=扇形ABB′的面积.
则阴影部分的面积是:
=6π
故选B.
【总结升华】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.即可求解.
举一反三:
【变式】某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案“我的宝贝”,图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作的半圆,如图所示,则图中阴影部分的面积为(
).
A.
B.72
C.36
D.72
【答案】本题解法很多,如两个小半圆面积和减去两个弓形面积等.
但经过认真观察等腰直角三角形其对称性可知,
阴影部分的面积由两个小半圆面积与三角形面积的和减去大半圆面积便可求得,
所以由已知得直角边为,小半圆半径为(cm),
因此阴影部分面积为.
故选C.
PAGE
【要点梳理】
要点一、圆的定义、性质及与圆有关的角
1.圆的定义
(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.
(2)圆是到定点的距离等于定长的点的集合.
(3)不在同一条直线上的三个点确定一个圆.
要点诠释:
①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;
②圆是一条封闭曲线.
2.点与圆的位置关系
判定一个点P是否在⊙O上
设⊙O的半径为,OP=,则有
点P在⊙O
外; 点P在⊙O
上;点P在⊙O
内.
要点诠释:
点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.
3.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
定理2:平分弧的直径垂直平分弧所对的弦.
4.与圆有关的角
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
在同圆或者等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.
在同圆或者等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
5.
圆内接四边形
圆内接四边形的对角互补.
要点二、图形的旋转
在平面内,一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的角叫做旋转角.
图形经过旋转所得的图形和原图形全等.
对应点到旋转中心的距离相等.任何一对对应点与旋转中心连线所成的角度等于旋转的角度.
要点三、正多边形
各边相等,各内角也相等的多边形是正多边形.
要点诠释:
判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).
正多边形的外接圆和圆的内接正多边形
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
要点四、弧长及扇形的面积
圆心角为、半径为R的弧长.
圆心角为,半径为R,弧长为的扇形的面积.
要点诠释:
(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,
即;
(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.
(3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;
(4)扇形两个面积公式之间的联系:.
【典型例题】
类型一、圆的基础知识
1.
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点在数轴上运动,若过点P且与OA平行(或重合)的直线与⊙O有公共点,
设OP=x,则的取值范围是(
).
A.-1≤≤1
B.≤≤
C.0≤≤
D.>
【答案】C;
【解析】如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,
由切线的性质,得∠OQP′=90°,
∵OA∥P′Q,
∴∠OP′Q=∠AOB=45°,
∴△OQP′为等腰直角三角形,
在Rt△OQP′中,OQ=1,
OP′=,
∴当过点P且与OA平行的直线与⊙O有公共点时,0≤OP≤,
当点P在x轴负半轴即点P向左侧移动时,结果相同.
故答案为:0≤OP≤.
【总结升华】本题考查了直线与圆的位置关系问题.关键是通过平移,确定直线与圆相切的情况,求出此时OP的值.
举一反三:
【变式】如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是( ).
A.-1≤x<0或0<x≤1
B.0<x≤1
C.-≤x<0或0<x≤
D.x>1
【答案】∵⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,
∴过点P′且与OB平行的直线与⊙O相切时,假设切点为D,
∴OD=DP′=1,
OP′=,
∴0<OP≤,
同理可得,当OP与x轴负半轴相交时,
-≤OP<0,
∴-≤OP<0,或0<OP≤.
故选C.
类型二、弧、弦、圆心角、圆周角的关系及垂径定理
2.如图所示,已知在⊙O中,AB是⊙O的直径,弦CG⊥AB于D,F是⊙O上的点,且,BF交CG于点E,求证:CE=BE.
【答案与解析】
证法一:如图(1),连接BC,
∵
AB是⊙O的直径,弦CG⊥AB,∴
.
∵
,∴
.∴
∠C=∠CBE.∴
CE=BE.
证法二:如图(2),作ON⊥BF,垂足为N,连接OE.
∵
AB是⊙O的直径,且AB⊥CG,∴
.
∵
,∴
.∴
BF=CG,ON=OD.
∵
∠ONE=∠ODE=90°,OE=OE,ON=OD,
∴
△ONE≌△ODE,∴
NE=DE.
∵
,,
∴
BN=CD,∴
BN-EN=CD-ED,∴
BE=CE.
证法三:如图(3),连接OC交BF于点N.
∵
,∴
OC⊥BF.
∵
AB是⊙O的直径,CG⊥AB,
∵
,.∴
,.
∵
OC=OB,∴
OC-ON=OB-OD,即CN=BD.
又∠CNE=∠BDE=90°,∠CEN=∠BED,
∴
△CNE≌△BDE,∴
CE=BE.
【总结升华】上述各种证明方法,虽然思路各异,但都用到了垂径定理及其推论.在平时多进行一题多解、一题多证、一题多变的练习,这样不但能提高分析问题的能力,而且还是沟通知识体系、学习知识,使用知识的好方法.
举一反三:
【变式】如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为(
)
A.19
B.16
C.18
D.20
【答案】如图,延长AO交BC于点D,过O作OE⊥BC于E.
则三角形ABD为等边三角形,DA=AB=BD=12,OD=AD-AO=4
在Rt△ODE中,∠ODE=60°,∠DOE=30°,则DE=OD=2,BE=BD-DE=10
OE垂直平分BC,BC=2BE=20.
故选D
类型三、图形的旋转
3.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
A.4,30°
B.2,60°
C.1,30°
D.3,60°
【思路点拨】利用旋转和平移的性质得出,∠A′B′C=60°,AB=A′B′=A′C=4,进而得出△A′B′C是等边三角形,即可得出BB′以及∠B′A′C的度数.
【答案】B;
解:∵∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,
∴∠A′B′C=60°,AB=A′B′=A′C=4,
∴△A′B′C是等边三角形,
∴B′C=4,∠B′A′C=60°,
∴BB′=6-4=2,
∴平移的距离和旋转角的度数分别为:2,60°.
【总结升华】此题主要考查了平移和旋转的性质以及等边三角形的判定等知识,得出△A′B′C是等边三角形是解题关键.
类型四、圆中有关的计算
4.(2016?绵阳)如图,AB为⊙O直径,C为⊙O上一点,点D是的中点,DE⊥AC于E,DF⊥AB于F.
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度.
【思路点拨】(1)先连接OD、AD,根据点D是的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;
(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.
【答案与解析】
解:(1)DE与⊙O相切.
证明:连接OD、AD,
∵点D是的中点,
∴=,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AC,
∴DE⊥OD,
∴DE与⊙O相切.
(2)连接BC交OD于H,延长DF交⊙O于G,
由垂径定理可得:OH⊥BC,==,
∴=,
∴DG=BC,
∴弦心距OH=OF=4,
∵AB是直径,
∴BC⊥AC,
∴OH∥AC,
∴OH是△ABC的中位线,
∴AC=2OH=8.
【点评】本题主要考查了直线与圆的位置关系,在判定一条直线为圆的切线时,当已知条件中明确指出直线与圆有公共点时,通常连接过该公共点的半径,证明该半径垂直于这条直线.本题也可以根据△ODF与△ABC相似,求得AC的长.
举一反三:
【变式】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
【答案】解:(1)∵OF⊥AB,
∴∠BOF=90°,
∵∠B=30°,FO=2,
∴OB=6,AB=2OB=12,
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC=AB=6;
(2)∵由(1)可知,AB=12,
∴AO=6,即AC=AO,
在Rt△ACF和Rt△AOF中,
∴Rt△ACF≌Rt△AOF,
∴∠FAO=∠FAC=30°,
∴∠DOB=60°,
过点D作DG⊥AB于点G,
∵OD=6,∴DG=3,
∴S△ACF+S△OFD=S△AOD=×6×3=9,
即阴影部分的面积是9.
类型五、圆与其他知识的综合运用
5..
【答案与解析】
延长DB至点E,使BE=DC,连结AE
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°,AB=AC
∴∠ADB=∠ACB=60°
∵四边形ABDC是圆内接四边形
∴∠ABE=∠ACD
在△AEB和△ADC中,
∴△AEB≌△ADC
∴AE=AD
∵∠ADB=60°
∴△AED是等边三角形
∴AD=DE=DB+BE
∵BE=DC
∴DB+DC=DA.
【总结升华】由已知条件,等边△ABC可得60°角,根据圆的性质,可得∠ADB=60°,利用截长补短的方法可得一个新的等边三角形,再证两个三角形全等,从而转移线段DC.
本例也可以用其他方法证明.如:
(1)延长DC至F,使CF=BD,连结AF,再证△ACF≌△ABD,得出AD=DF,从而DB+CD=DA.
(2)在DA上截取DG=DC,连结CG,再证△BDC≌△AGC,得出BD=AG,从而DB+CD=DA.
6.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是(
).
A.
3
B.
6
C.
5
D.
4
【答案】B;
【解析】阴影部分的面积
=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积
=扇形ABB′的面积.
则阴影部分的面积是:
=6π
故选B.
【总结升华】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.即可求解.
举一反三:
【变式】某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案“我的宝贝”,图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作的半圆,如图所示,则图中阴影部分的面积为(
).
A.
B.72
C.36
D.72
【答案】本题解法很多,如两个小半圆面积和减去两个弓形面积等.
但经过认真观察等腰直角三角形其对称性可知,
阴影部分的面积由两个小半圆面积与三角形面积的和减去大半圆面积便可求得,
所以由已知得直角边为,小半圆半径为(cm),
因此阴影部分面积为.
故选C.
PAGE
同课章节目录
