6.1矩形

(共25张PPT)
数学八年级下：6.1《矩形》优秀课件
观察平行四边形的框架,回答下列问题:
(1) 为什么这个框架会任意”摇摆”
(2) 随着内角的变化情况,平行四边形的边,角,周长, 面积等发生了什么变化
(3) 当内角为直角时所成的四边形你认识吗
矩形：
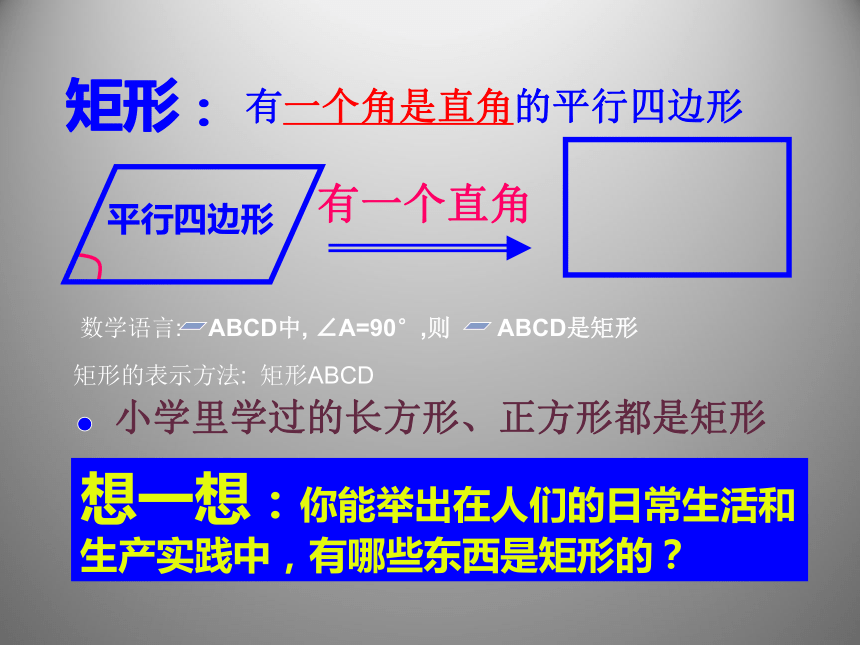
有一个角是直角的平行四边形
小学里学过的长方形、正方形都是矩形
矩形：
想一想：你能举出在人们的日常生活和
生产实践中，有哪些东西是矩形的？
数学语言: ABCD中, ∠A=90°,则 ABCD是矩形
矩形的表示方法: 矩形ABCD
有一个直角
平行四边形
探索矩形的性质
第1课时—矩形的性质
(1) 矩形是不是平行四边形
(2) 平行四边形是不是矩形
(3) 平行四边形的性质矩形具备吗
(4) 矩形是否有与平行四边形不同的性质
实质上：矩形是特殊的平行四边形。
既然矩形是特殊的平行四边形，那么它和平行四边形相比特殊在哪里？哪些性质改变了，哪些未性质改变？
对角相等，邻角互补
对边平行且相等
对角线互相平分
元素 平行四边形的性质
中心对称
角
边
对角线
对称性
四个角都是角
邻边互相垂直
对角线互相平
分且相等
元素 平行四边形的性质 矩形的性质
角 对角相等，邻角互补
边 对边平行且相等
对角线 对角线互相平分
对称性 中心对称图形
既是中心对称,
也是轴对称图形
A
B
C
D
已知：四边形ABCD是矩形，∠A＝900
求证：∠A= ∠B = ∠C=∠D=900
证明：∵ 四边形ABCD是矩形
∴ AD∥BC
∴ ∠A+ ∠B=1800
又∵ ∠A＝900
∴ ∠B ＝900
又∵ ∠A = ∠C， ∠B = ∠D（矩形的对角相等）
∴ ∠A= ∠B = ∠C=∠D=900
矩形的四个角都是直角
猜想1
矩形的性质定理1
已知：AC，BD是矩形ABCD的对角线
求证：AC=BD
O
A
B
C
D
想一想,还有没有其他的证明方法
猜想2 矩形的对角线相等
矩形的性质定理2
证明：
A
B
C
D
O
已知：AC,BD是矩形的对角线
求证：AC=BD
由题知 OA=OC, OB=OD
即 BD = AC .
∴ OB+OD=
AC+
AC = AC,
∴ OB=
AC，OD=
AC，
（为什么 ）
且 ∠ABC=∠ADC=Rt∠,
(为什么 )
A
B
C
D
O
矩形的对称性:
矩形是中心对称图形,又是轴对称图形。
矩形的对称中心在哪？
矩形是对称轴有几条
四个角都是直角 　　　　
邻边：互相垂直
A
B
C
D
互相平分
　　　 　　　　
平行
对边 相等
　　　　 　　　　
O
矩形特征总结：
（3）对角线：
（2）角：
（1）边：
相等
（共性）
（共性）
（共性）
（特性）
（4）对称性：
中心对称
（共性）
（特性）
轴对称
（特性）
（特性）
矩形具有而一般平行四边形不具有的性质是（ ）.
A 对角线相等 B 对边相等
A
C 对角相等 D 对角线互相平分
O
D
C
B
A
矩形ABCD中，已知AB=8㎝，AD=6㎝，
则OB=____ ㎝，若已知∠CAB=40°，
则 ∠OBA=____ ∠AOD=____
5
40°
80°
40°
图中有几个等腰三角形？几对全等三角形
O
A
B
C
D
若已知AB=6, BC=8，
求矩形的面积，周长，对角线的长度。
若已知BC=8， O到AD的距离为3，
求矩形的面积，周长，对角线的长度。
根据矩形的上述性质，
你能发现OA、OB、OC、OD有什么
关系？
OA=OB=OC=OD ;
已知矩形的周长是14,相邻两边的差是1,
那么这个矩形的面积是多少？
Ａ
Ｂ
Ｄ
Ｃ
Ｏ
“六一”儿童节快到了，现在想在我们教室上方挂一盏
彩灯，要求彩灯到四个墙角的距离相等。请你帮忙确定
彩灯的位置。
（1）若∠AOD=100度,则∠OAD=
（3）若∠AOD=120°且AB=4，试求出对角线的长。
100°
（2）若上图中∠AOD=120°，试判断△AOB的形状。
120°
已知: 在矩形ABCD中,E、F分别是AB、CD的中点.
求证：四边形AEFD是矩形.
（2）
分析: 矩形的定义是什么
先证 四边形AEFD是平行四边形,
再证 其有一个角是直角就可以得证
已知:如图,过矩形ABCD的顶点作CE//BD， 交AB的延长线于E。 求证：∠CAE=∠CEA
A
B
C
D
E
相信你,一定行
已知:如图,在矩形ABCD中,M为BC的中点。
求证:AM=DM.
M
D
A
B
C
若要使∠AMD是直角，应增加什么条件？
相信你,一定行
小结 反思
1.一个定义：
2.二个定理:
3.二个结论:
(1)矩形的两条对角线被交点分成的四条线段相等
(2)矩形既是轴对称图形，又是中心对称图形
这节课你学到了什么 还有什么困惑吗？
四个角都是直角 　　　　
邻边：互相垂直
A
B
C
D
互相平分
　　　 　　　　
平行
对边 相等
　　　　 　　　　
O
矩形特征总结：
（3）对角线：
（2）角：
（1）边：
相等
（共性）
（共性）
（共性）
（特性）
（4）对称性：
中心对称
（共性）
（特性）
轴对称
（特性）
（特性）