2020年浙教版九年级数学第4章 相似三角形单元综合测试卷(Word版,含解析)
文档属性
| 名称 | 2020年浙教版九年级数学第4章 相似三角形单元综合测试卷(Word版,含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 198.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 10:40:54 | ||
图片预览


文档简介
2020年浙教版九年级数学第4章
相似三角形单元综合测试卷解析版
一、选择题(共10题;共30分)
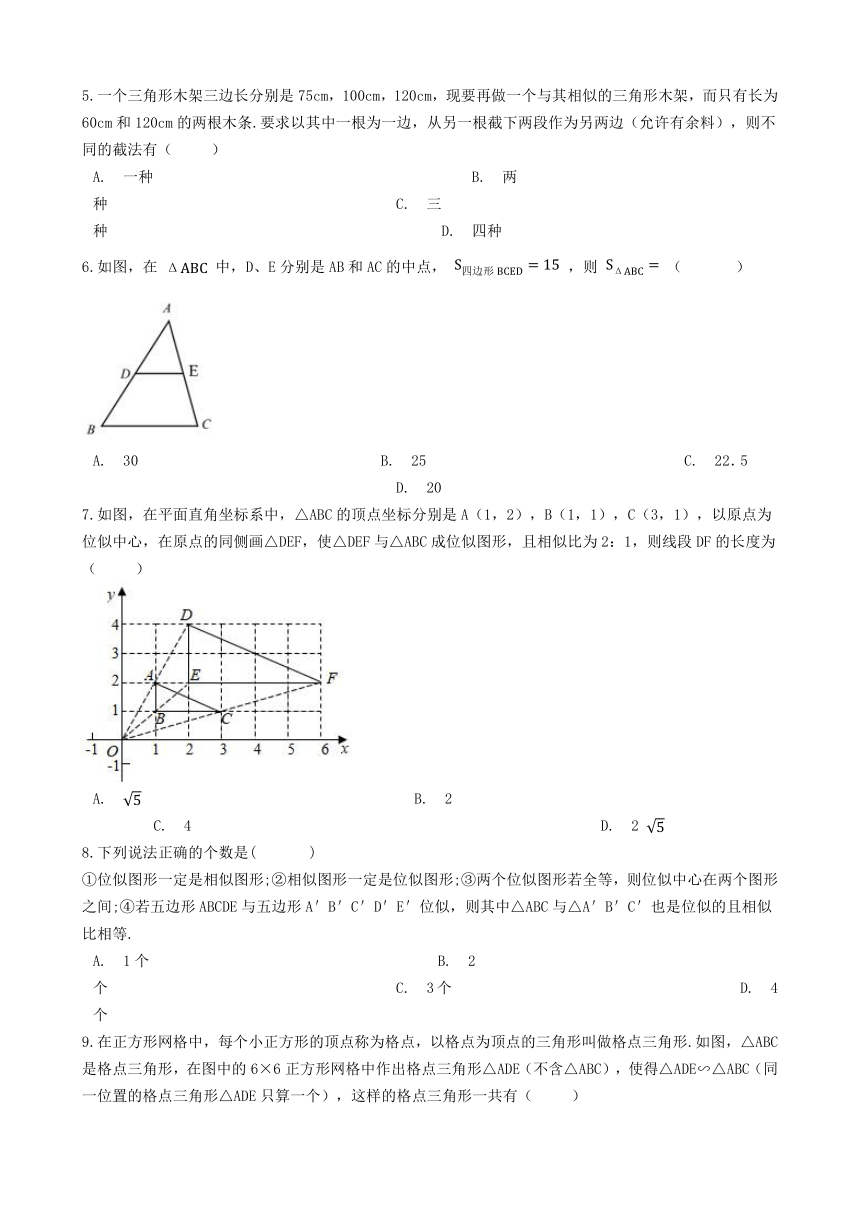
1.已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是(
???)
??????
A.?1????????????
??????????B.?2.25?????
?????C.?4????????
?????D.?2
2.如图,在△ABC中,DE∥AB,且
=
,则
的值为(??
)
A.???????????????????B.???????????????????????????C.??????????????????????????????D.?
3.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E
,
交AD于点F
,
交CD的延长线于点G
,
若AF=2FD
,
则
的值为(???
)
A.??????????????????????B.????????????????????????????C.??????????????????????????D.?
4.生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果
,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为(??
)
A.?????????????????????B.??????????????????????C.???????????????????D.?
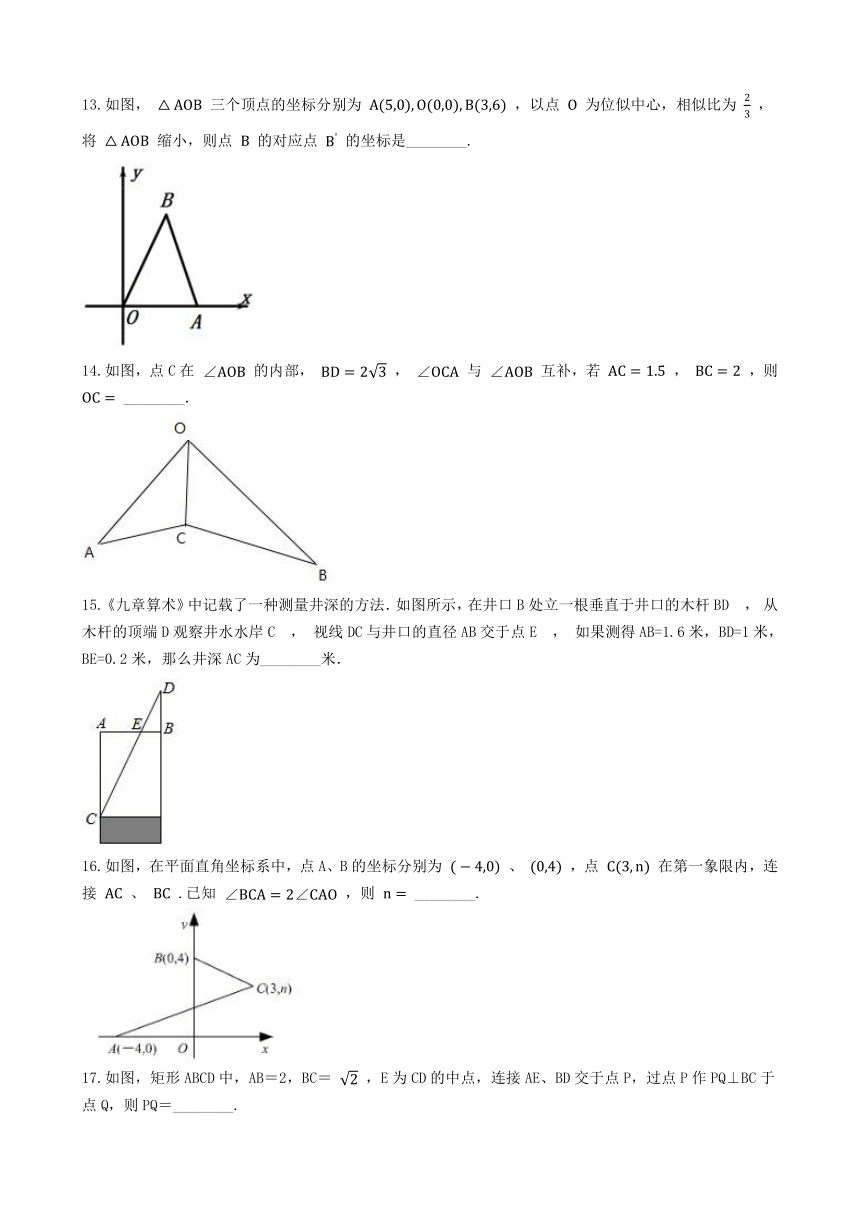
5.一个三角形木架三边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有(??
)
A.?一种?????????????????????B.?两种???????????????????C.?三种??????????????????????D.?四种
6.如图,在
中,D、E分别是AB和AC的中点,
,则
(???
)
A.?30????????????????B.?25?????????????????C.?22.5??????????????????????D.?20
7.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为(??
)
A.???????????????????B.?2?????????????????????????C.?4???????????????????????????D.?2
8.下列说法正确的个数是(???
)
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.
A.?1个???????????????????B.?2个???????????????????C.?3个???????????????????D.?4个
9.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有(??
)
A.?4个???????????????????????B.?5个?????????????????????C.?6个?????????????????????D.?7个
10.如图,正方形
中,点F是
边上一点,连接
,以
为对角线作正方形
,边
与正方形
的对角线
相交于点H,连接
.以下四个结论:①
;②
;③
;④
.其中正确的个数为(??
)
A.?1个??????????????????????B.?2个??????????????????????C.?3个?????????????????????????????????D.?4个
二、填空题(共8题;共24分)
11.如图,在
与
中,
,要使
与
相似,还需添加一个条件,这个条件可以是________(只需填一个条件)
12.如图,
.若
,
,则
________.
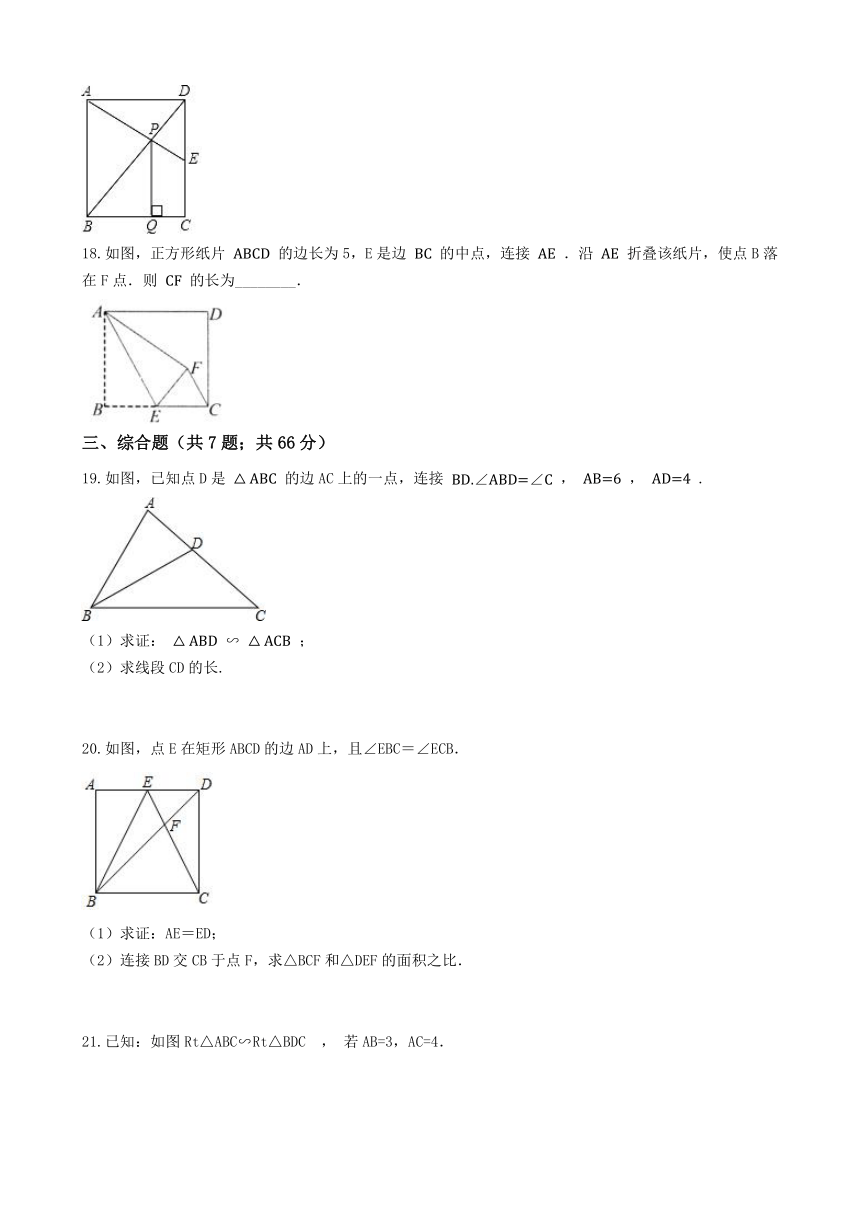
13.如图,
三个顶点的坐标分别为
,以点
为位似中心,相似比为
,将
缩小,则点
的对应点
的坐标是________.
14.如图,点C在
的内部,
,
与
互补,若
,
,则
________.
15.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD
,
从木杆的顶端D观察井水水岸C
,
视线DC与井口的直径AB交于点E
,
如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为________米.
16.如图,在平面直角坐标系中,点A、B的坐标分别为
、
,点
在第一象限内,连接
、
.已知
,则
________.
17.如图,矩形ABCD中,AB=2,BC=
,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
18.如图,正方形纸片
的边长为5,E是边
的中点,连接
.沿
折叠该纸片,使点B落在F点.则
的长为________.
三、综合题(共7题;共66分)
19.如图,已知点D是
的边AC上的一点,连接
,
,
.
(1)求证:
∽
;
(2)求线段CD的长.
20.如图,点E在矩形ABCD的边AD上,且∠EBC=∠ECB.
(1)求证:AE=ED;
(2)连接BD交CB于点F,求△BCF和△DEF的面积之比.
21.已知:如图Rt△ABC∽Rt△BDC
,
若AB=3,AC=4.
(1)求BD、CD的长;
(2)过B作BE⊥DC于E
,
求BE的长.
22.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1
,
与△OAB对应线段的比为2:1,画出△OA1B1
,
(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标________;
23.如图,AE为△ABC外接圆⊙O的直径,AD为△ABC的高.
求证:
(1)∠BAD=∠EAC;
(2)AB?AC=AD?AE
24.已知:如图,在△ABC中,AB=AC
,
点D、E分别在边BC、DC上,AB2
=BE
·
DC
,
DE:EC=3:1
,
F是边AC上的一点,DF与AE交于点G
.
(1)找出图中与△ACD相似的三角形,并说明理由;
(2)当DF平分∠ADC时,求DG:DF的值;
(3)如图,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.
25.如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=
,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式;
(2)当线段DF的长度最大时,求D点的坐标;
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与
相似?若存在,求出m的值;若不存在,请说明理由.
答案
选择题
1.解:A、1.5×2=3×1,故A不符合题意;
B、1.5×3=2×2.25,故B不符合题意;
C、2×3=1.5×4,故C不符合题意;
D、
1.5,2,3,2不能组成比例线段,
故D符合题意.
故答案为:D.
2.解:∵DE//AB,
∴
∴
的值为
.
故答案为:A.
3.解:由AF=2DF
,
可以假设DF=k
,
则AF=2k
,
AD=3k
,
∵四边形ABCD是平行四边形,
∴AD∥BC
,
AB∥CD
,
AB=CD
,
∴∠AFB=∠FBC=∠DFG
,
∠ABF=∠G
,
∵BE平分∠ABC
,
∴∠ABF=∠CBG
,
∴∠ABF=∠AFB=∠DFG=∠G
,
∴AB=CD=2k
,
DF=DG=k
,
∴CG=CD+DG=3k
,
∵AB∥DG
,
∴△ABE∽△CGE
,
∴
,
故答案为:C
.
4.解:根据黄金分割点的概念得:AC=
∴BC=AB-AC=?
;
故答案为:B.
5.解:长120cm的木条与三角形木架的最长边相等,则长120cm的木条不能作为一边,
设从120cm的木条上截下两段长分别为xcm,ycm(x+y≤120),
由于长60cm的木条不能与75cm的一边对应,否则x、y有大于120cm,
当长60cm的木条与100cm的一边对应,则
,
解得:x=45,y=72;
当长60cm的木条与120cm的一边对应,则
,
解得:x=37.5,y=50.
答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段.
故答案为:B.
6.解:根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=
BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知
:
=1:4,则
:
=3:4,题中已知
,故可得
=5,
=20
故本题选择D
7.解:∵以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,
而A(1,2),C(3,1),
∴D(2,4),F(6,2),
∴DF=
=2
.
故答案为:D.
8.利用位似的定义可知,位似图形一定是相似图形,但是相似图形不一定是位似图形,因为它是一种特殊的相似,所以①符合题意,②不符合题意;
两个位似图形若全等,根据对应点一定相交于一点,可得到位似中心可能在两个图形之间,也可能在三角形内部或边上,所以③不符合题意;
若五边形ABCDE与五边形A1B1C1D1E1位似,则在五边形中连线组成△ABC与△A1B1C1
,
可得它也是位似且相似比相等,故④符合题意.
所以①④符合题意.
故答案为:B.
9.解:
ABC的三边之比为
,
如图所示,可能出现的相似三角形共有以下六种情况:
所以使得△ADE∽△ABC的格点三角形一共有6个,
故答案为:C.
10.解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①符合题意
②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC=
AD,AF=
AG
∴
,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②符合题意
③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF=
AE
∴
∴③符合题意
④由②知
又∵四边形ABCD为正方形,
AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④符合题意
故答案为:D.
二、填空题
11.添加条件:∠B=∠E;
∵
,∠B=∠E,
∴△ABC∽△AED,
故答案为:∠B=∠E(答案不唯一).
12.解:∵
,
∴
,
又∵
,
,
∴
,
∴
,
故答案为:10.
13.解:∵以点
为位似中心,相似比为
,将
缩小,
∴点
的对应点B′的坐标是(2,4)或(-2,-4).
故答案为:(2,4)或(-2,-4).
14.解:∵∠OCA=∠OCB,∠OCA与∠AOB互补,
∴∠OCA+∠AOB=180°,∠OCB+∠AOB=180°,
∵∠OCA+∠COA+∠OAC=180°,∠OCB+∠OBC+∠COB=180°,
∴∠AOB=∠COA+∠OAC,∠AOB=∠OBC+∠COB,
∴∠AOC=∠OBC,∠COB=∠OAC,
∴△ACO∽△OCB,
∴
,
∴OC2=2×
=3,
∴OC=
,
故答案为:
.
15.解:∵BD⊥AB
,
AC⊥AB
,
∴BD
AC
,
∴△ACE∽△DBE
,
∴
,
∴
,
∴AC=7(米),
故答案为:7(米).
16.解:如图,过点C作CD⊥y轴,交y轴于点D,则CD∥AO,
∴∠DCE=∠CAO,
∵∠BCA=2∠CAO,
∴∠BCA=2∠DCE,
∴∠DCE=∠DCB,
∵CD⊥y轴,
∴∠CDE=∠CDB=90°,
又∵CD=CD,
∴
CDE≌
CDB(ASA),
∴DE=DB,
∵B(0,4),C(3,n),
∴CD=3,OD=n,OB=4,
∴DE=DB=OB-OD=4-n,
∴OE=OD-DE
=n-(4-n)
=2n-4,
∵A(-4,0),
∴AO=4,
∵CD∥AO,
∴
AOE∽
CDE,
∴
,
∴
,
解得:
,
故答案为:
.
17.解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE=
CD=
AB,
∴△ABP∽△EDP,
∴
=
,
∴
=
,
∴
=
,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴
=
=
,
∵CD=2,
∴PQ=
,
故答案为:
.
18.根据折叠的性质,△ABE
△BFE,AE垂直平分BF,且E是边BC的中点,
∴BE=EF=EC,∠BEA=∠FEA,
∴∠EFC=∠ECF,
∵∠BEF
=∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF,
∴AE∥FC,
∵四边形
是边长为5的正方形,且E是边BC的中点,
∴∠ABC=90
,AB=5,BE=
,
∴
,
连接BF交AE于点G,如图:
∵AE垂直平分BF,
∴∠BGE=90
,
∴Rt△EBG∽Rt△EAB,
∴
,即
,
∴
,
∵GE∥FC,E是边BC的中点,
∴CF=2GE=
,
故答案为:
.
三、解答题
19.(1)解:∵∠ABD=∠C,∠A=∠A(公共角),
∴△ABD∽△ACB
(2)解:由(1)知:△ABD∽△ACB,
∵相似三角形的对应线段成比例
,∴
=
,即
=
,
解得:CD=5
20.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠CDE=90°,
∵∠EBC=∠ECB,
∴EB=EC,
∴Rt△ABE≌Rt△DCE(HL),
∴AE=ED
(2)解:∵BC=AD,AE=ED,
∴BC=2DE,
∵DE∥BC,
∴△DEF∽△BCF,
∴
21.
(1)解:Rt△ABC中,根据勾股定理得:BC=
=5,
∵Rt△ABC∽Rt△BDC,
∴
,
,
∴BD=
,CD=
(2)解:在Rt△BDC中,
S△BDC=
BE?CD=
BD?BC,
∴BE=
=
=3
22.
(1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)
解:(1)由图2可知,A1、B1的坐标为(4,0)和(2,﹣4);
故答案为:(4,0)和(2,﹣4);
23.
(1)证明:如图,连接CE,
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD+∠B=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠EAC+∠E=90°,
又∵∠B=∠E,
∴∠BAD=∠EAC
(2)在△ABD与△AEC中,
,
∴△ABD∽△AEC,
∴,
∴AB?AC=AD?AE
24.
(1)解:与△ACD相似的三角形有:△ABE、△ADC,理由如下:
∵AB2
=BE
·
DC
,
∴
.
∵AB=AC,
∴∠B=∠C,
,
∴△ABE∽△DCA.
∴∠AED=∠DAC.
∵∠AED=∠C+∠EAC,∠DAC=∠DAE+∠EAC,
∴∠DAE=∠C.
∴△ADE∽△CDA
.
(2)解:∵△ADE∽△CDA,DF平分∠ADC,
∴
,
设CE=a,则DE=3CE=3a,CD=4a,
∴
,解得
(负值已舍)
∴
;
(3)解:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°
,
∴∠DAE=∠C=45°,
∵DG⊥AE,
∴∠DAG=∠ADF=45°,
∴AG=DG=
,
∴
,
∵∠AED=∠DAC
,
∴△ADE∽△DFA,
∴
,
∴
,
∴
.
25.
(1)解:设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(﹣t,0),
则x=
=
(2t﹣t),解得:t=1,
故点A、B的坐标分别为(2,0)、(﹣1,0),
则抛物线的表达式为:y=a(x﹣2)(x+1)=ax2+bx+2,
解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)解:对于y=﹣x2+x+2,令x=0,则y=2,故点C(0,2),
由点A、C的坐标得,直线AC的表达式为:y=﹣x+2,
设点D的横坐标为m,则点D(m,﹣m2+m+2),则点F(m,﹣m+2),
则DF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
∵﹣1<0,故DF有最大值,此时m=1,点D(1,2);
(3)解:存在,理由:
点D(m,﹣m2+m+2)(m>0),则OD=m,DE=﹣m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则
或
,即
=2或
,即
=2或
,
解得:m=1或﹣2(舍去)或
或
(舍去),
故m=1或
.
相似三角形单元综合测试卷解析版
一、选择题(共10题;共30分)
1.已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是(
???)
??????
A.?1????????????
??????????B.?2.25?????
?????C.?4????????
?????D.?2
2.如图,在△ABC中,DE∥AB,且
=
,则
的值为(??
)
A.???????????????????B.???????????????????????????C.??????????????????????????????D.?
3.如图,在平行四边形ABCD中,∠ABC的平分线交AC于点E
,
交AD于点F
,
交CD的延长线于点G
,
若AF=2FD
,
则
的值为(???
)
A.??????????????????????B.????????????????????????????C.??????????????????????????D.?
4.生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果
,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为(??
)
A.?????????????????????B.??????????????????????C.???????????????????D.?
5.一个三角形木架三边长分别是75cm,100cm,120cm,现要再做一个与其相似的三角形木架,而只有长为60cm和120cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有(??
)
A.?一种?????????????????????B.?两种???????????????????C.?三种??????????????????????D.?四种
6.如图,在
中,D、E分别是AB和AC的中点,
,则
(???
)
A.?30????????????????B.?25?????????????????C.?22.5??????????????????????D.?20
7.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为(??
)
A.???????????????????B.?2?????????????????????????C.?4???????????????????????????D.?2
8.下列说法正确的个数是(???
)
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也是位似的且相似比相等.
A.?1个???????????????????B.?2个???????????????????C.?3个???????????????????D.?4个
9.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有(??
)
A.?4个???????????????????????B.?5个?????????????????????C.?6个?????????????????????D.?7个
10.如图,正方形
中,点F是
边上一点,连接
,以
为对角线作正方形
,边
与正方形
的对角线
相交于点H,连接
.以下四个结论:①
;②
;③
;④
.其中正确的个数为(??
)
A.?1个??????????????????????B.?2个??????????????????????C.?3个?????????????????????????????????D.?4个
二、填空题(共8题;共24分)
11.如图,在
与
中,
,要使
与
相似,还需添加一个条件,这个条件可以是________(只需填一个条件)
12.如图,
.若
,
,则
________.
13.如图,
三个顶点的坐标分别为
,以点
为位似中心,相似比为
,将
缩小,则点
的对应点
的坐标是________.
14.如图,点C在
的内部,
,
与
互补,若
,
,则
________.
15.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD
,
从木杆的顶端D观察井水水岸C
,
视线DC与井口的直径AB交于点E
,
如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为________米.
16.如图,在平面直角坐标系中,点A、B的坐标分别为
、
,点
在第一象限内,连接
、
.已知
,则
________.
17.如图,矩形ABCD中,AB=2,BC=
,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=________.
18.如图,正方形纸片
的边长为5,E是边
的中点,连接
.沿
折叠该纸片,使点B落在F点.则
的长为________.
三、综合题(共7题;共66分)
19.如图,已知点D是
的边AC上的一点,连接
,
,
.
(1)求证:
∽
;
(2)求线段CD的长.
20.如图,点E在矩形ABCD的边AD上,且∠EBC=∠ECB.
(1)求证:AE=ED;
(2)连接BD交CB于点F,求△BCF和△DEF的面积之比.
21.已知:如图Rt△ABC∽Rt△BDC
,
若AB=3,AC=4.
(1)求BD、CD的长;
(2)过B作BE⊥DC于E
,
求BE的长.
22.如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1
,
与△OAB对应线段的比为2:1,画出△OA1B1
,
(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标________;
23.如图,AE为△ABC外接圆⊙O的直径,AD为△ABC的高.
求证:
(1)∠BAD=∠EAC;
(2)AB?AC=AD?AE
24.已知:如图,在△ABC中,AB=AC
,
点D、E分别在边BC、DC上,AB2
=BE
·
DC
,
DE:EC=3:1
,
F是边AC上的一点,DF与AE交于点G
.
(1)找出图中与△ACD相似的三角形,并说明理由;
(2)当DF平分∠ADC时,求DG:DF的值;
(3)如图,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.
25.如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x=
,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)求抛物线的表达式;
(2)当线段DF的长度最大时,求D点的坐标;
(3)抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与
相似?若存在,求出m的值;若不存在,请说明理由.
答案
选择题
1.解:A、1.5×2=3×1,故A不符合题意;
B、1.5×3=2×2.25,故B不符合题意;
C、2×3=1.5×4,故C不符合题意;
D、
1.5,2,3,2不能组成比例线段,
故D符合题意.
故答案为:D.
2.解:∵DE//AB,
∴
∴
的值为
.
故答案为:A.
3.解:由AF=2DF
,
可以假设DF=k
,
则AF=2k
,
AD=3k
,
∵四边形ABCD是平行四边形,
∴AD∥BC
,
AB∥CD
,
AB=CD
,
∴∠AFB=∠FBC=∠DFG
,
∠ABF=∠G
,
∵BE平分∠ABC
,
∴∠ABF=∠CBG
,
∴∠ABF=∠AFB=∠DFG=∠G
,
∴AB=CD=2k
,
DF=DG=k
,
∴CG=CD+DG=3k
,
∵AB∥DG
,
∴△ABE∽△CGE
,
∴
,
故答案为:C
.
4.解:根据黄金分割点的概念得:AC=
∴BC=AB-AC=?
;
故答案为:B.
5.解:长120cm的木条与三角形木架的最长边相等,则长120cm的木条不能作为一边,
设从120cm的木条上截下两段长分别为xcm,ycm(x+y≤120),
由于长60cm的木条不能与75cm的一边对应,否则x、y有大于120cm,
当长60cm的木条与100cm的一边对应,则
,
解得:x=45,y=72;
当长60cm的木条与120cm的一边对应,则
,
解得:x=37.5,y=50.
答:有两种不同的截法:把120cm的木条截成45cm、72cm两段或把120cm的木条截成37.5cm、50cm两段.
故答案为:B.
6.解:根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=
BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知
:
=1:4,则
:
=3:4,题中已知
,故可得
=5,
=20
故本题选择D
7.解:∵以原点为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,
而A(1,2),C(3,1),
∴D(2,4),F(6,2),
∴DF=
=2
.
故答案为:D.
8.利用位似的定义可知,位似图形一定是相似图形,但是相似图形不一定是位似图形,因为它是一种特殊的相似,所以①符合题意,②不符合题意;
两个位似图形若全等,根据对应点一定相交于一点,可得到位似中心可能在两个图形之间,也可能在三角形内部或边上,所以③不符合题意;
若五边形ABCDE与五边形A1B1C1D1E1位似,则在五边形中连线组成△ABC与△A1B1C1
,
可得它也是位似且相似比相等,故④符合题意.
所以①④符合题意.
故答案为:B.
9.解:
ABC的三边之比为
,
如图所示,可能出现的相似三角形共有以下六种情况:
所以使得△ADE∽△ABC的格点三角形一共有6个,
故答案为:C.
10.解:①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG,∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①符合题意
②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC,AG=FG
∴AC=
AD,AF=
AG
∴
,
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②符合题意
③∵四边形AEFG和四边形ABCD均为正方形,AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF=
AE
∴
∴③符合题意
④由②知
又∵四边形ABCD为正方形,
AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④符合题意
故答案为:D.
二、填空题
11.添加条件:∠B=∠E;
∵
,∠B=∠E,
∴△ABC∽△AED,
故答案为:∠B=∠E(答案不唯一).
12.解:∵
,
∴
,
又∵
,
,
∴
,
∴
,
故答案为:10.
13.解:∵以点
为位似中心,相似比为
,将
缩小,
∴点
的对应点B′的坐标是(2,4)或(-2,-4).
故答案为:(2,4)或(-2,-4).
14.解:∵∠OCA=∠OCB,∠OCA与∠AOB互补,
∴∠OCA+∠AOB=180°,∠OCB+∠AOB=180°,
∵∠OCA+∠COA+∠OAC=180°,∠OCB+∠OBC+∠COB=180°,
∴∠AOB=∠COA+∠OAC,∠AOB=∠OBC+∠COB,
∴∠AOC=∠OBC,∠COB=∠OAC,
∴△ACO∽△OCB,
∴
,
∴OC2=2×
=3,
∴OC=
,
故答案为:
.
15.解:∵BD⊥AB
,
AC⊥AB
,
∴BD
AC
,
∴△ACE∽△DBE
,
∴
,
∴
,
∴AC=7(米),
故答案为:7(米).
16.解:如图,过点C作CD⊥y轴,交y轴于点D,则CD∥AO,
∴∠DCE=∠CAO,
∵∠BCA=2∠CAO,
∴∠BCA=2∠DCE,
∴∠DCE=∠DCB,
∵CD⊥y轴,
∴∠CDE=∠CDB=90°,
又∵CD=CD,
∴
CDE≌
CDB(ASA),
∴DE=DB,
∵B(0,4),C(3,n),
∴CD=3,OD=n,OB=4,
∴DE=DB=OB-OD=4-n,
∴OE=OD-DE
=n-(4-n)
=2n-4,
∵A(-4,0),
∴AO=4,
∵CD∥AO,
∴
AOE∽
CDE,
∴
,
∴
,
解得:
,
故答案为:
.
17.解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,AD=BC,∠BAD=90°,
∵E为CD的中点,
∴DE=
CD=
AB,
∴△ABP∽△EDP,
∴
=
,
∴
=
,
∴
=
,
∵PQ⊥BC,
∴PQ∥CD,
∴△BPQ∽△DBC,
∴
=
=
,
∵CD=2,
∴PQ=
,
故答案为:
.
18.根据折叠的性质,△ABE
△BFE,AE垂直平分BF,且E是边BC的中点,
∴BE=EF=EC,∠BEA=∠FEA,
∴∠EFC=∠ECF,
∵∠BEF
=∠BEA+∠FEA=∠EFC+∠ECF,
∴∠BEA=∠ECF,
∴AE∥FC,
∵四边形
是边长为5的正方形,且E是边BC的中点,
∴∠ABC=90
,AB=5,BE=
,
∴
,
连接BF交AE于点G,如图:
∵AE垂直平分BF,
∴∠BGE=90
,
∴Rt△EBG∽Rt△EAB,
∴
,即
,
∴
,
∵GE∥FC,E是边BC的中点,
∴CF=2GE=
,
故答案为:
.
三、解答题
19.(1)解:∵∠ABD=∠C,∠A=∠A(公共角),
∴△ABD∽△ACB
(2)解:由(1)知:△ABD∽△ACB,
∵相似三角形的对应线段成比例
,∴
=
,即
=
,
解得:CD=5
20.
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠CDE=90°,
∵∠EBC=∠ECB,
∴EB=EC,
∴Rt△ABE≌Rt△DCE(HL),
∴AE=ED
(2)解:∵BC=AD,AE=ED,
∴BC=2DE,
∵DE∥BC,
∴△DEF∽△BCF,
∴
21.
(1)解:Rt△ABC中,根据勾股定理得:BC=
=5,
∵Rt△ABC∽Rt△BDC,
∴
,
,
∴BD=
,CD=
(2)解:在Rt△BDC中,
S△BDC=
BE?CD=
BD?BC,
∴BE=
=
=3
22.
(1)解:如图2,△OA1B1即为所求;
(2)(4,0)和(2,﹣4)
解:(1)由图2可知,A1、B1的坐标为(4,0)和(2,﹣4);
故答案为:(4,0)和(2,﹣4);
23.
(1)证明:如图,连接CE,
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD+∠B=90°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∴∠EAC+∠E=90°,
又∵∠B=∠E,
∴∠BAD=∠EAC
(2)在△ABD与△AEC中,
,
∴△ABD∽△AEC,
∴,
∴AB?AC=AD?AE
24.
(1)解:与△ACD相似的三角形有:△ABE、△ADC,理由如下:
∵AB2
=BE
·
DC
,
∴
.
∵AB=AC,
∴∠B=∠C,
,
∴△ABE∽△DCA.
∴∠AED=∠DAC.
∵∠AED=∠C+∠EAC,∠DAC=∠DAE+∠EAC,
∴∠DAE=∠C.
∴△ADE∽△CDA
.
(2)解:∵△ADE∽△CDA,DF平分∠ADC,
∴
,
设CE=a,则DE=3CE=3a,CD=4a,
∴
,解得
(负值已舍)
∴
;
(3)解:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°
,
∴∠DAE=∠C=45°,
∵DG⊥AE,
∴∠DAG=∠ADF=45°,
∴AG=DG=
,
∴
,
∵∠AED=∠DAC
,
∴△ADE∽△DFA,
∴
,
∴
,
∴
.
25.
(1)解:设OB=t,则OA=2t,则点A、B的坐标分别为(2t,0)、(﹣t,0),
则x=
=
(2t﹣t),解得:t=1,
故点A、B的坐标分别为(2,0)、(﹣1,0),
则抛物线的表达式为:y=a(x﹣2)(x+1)=ax2+bx+2,
解得:a=﹣1,
故抛物线的表达式为:y=﹣x2+x+2;
(2)解:对于y=﹣x2+x+2,令x=0,则y=2,故点C(0,2),
由点A、C的坐标得,直线AC的表达式为:y=﹣x+2,
设点D的横坐标为m,则点D(m,﹣m2+m+2),则点F(m,﹣m+2),
则DF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
∵﹣1<0,故DF有最大值,此时m=1,点D(1,2);
(3)解:存在,理由:
点D(m,﹣m2+m+2)(m>0),则OD=m,DE=﹣m2+m+2,
以点O,D,E为顶点的三角形与△BOC相似,
则
或
,即
=2或
,即
=2或
,
解得:m=1或﹣2(舍去)或
或
(舍去),
故m=1或
.
同课章节目录
