3.1圆(1)

(共22张PPT)
3.1 圆(第一课时)
圆的世界
酸酸甜甜就是我
水波荡漾
动动手、
1、请同学们在纸上画
一个半径为2cm的圆．
2、如果我们的体育老师想在操场
上画一个半半径为3m的圆，
你有什么好的办法或建议吗？
动动脑
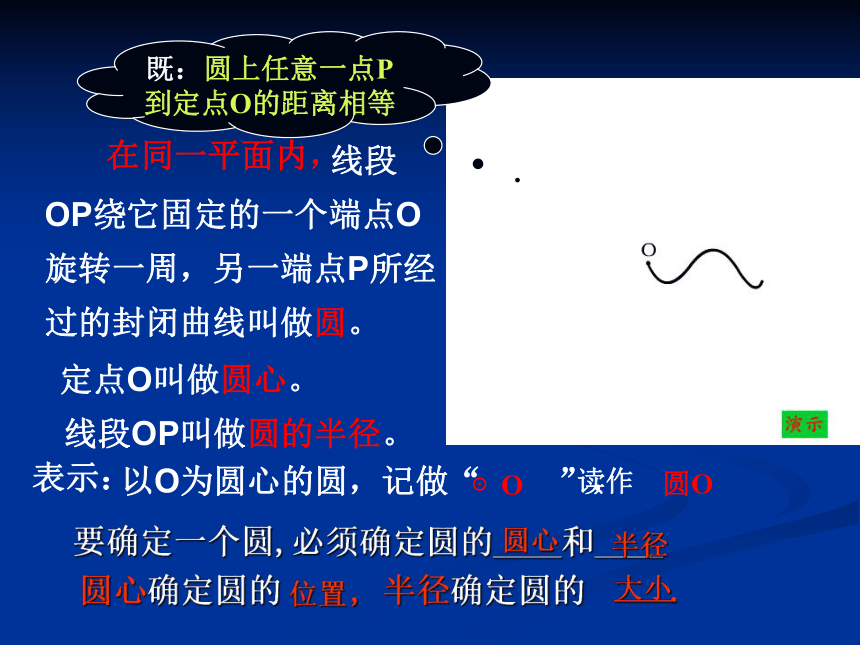
线段OP绕它固定的一个端点O旋转一周，另一端点P所经过的封闭曲线叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
在同一平面内，
感悟新知
要确定一个圆,必须确定圆的____和____
圆心
半径
读做“ ”。
⊙O
圆O
圆心确定圆的 , 半径确定圆的 .
位置
大小
既：圆上任意一点P到定点O的距离相等
表示：
以O为圆心的圆，记做“ ”，
读作
1、请将自己所画的圆与同桌所画的圆进行比较， 它们是否能够完全重合？并思考什么情况下两个圆能够完全重合？
O1
r
O2
r
半径相等的两个圆叫做等圆。
动手做一做
半径相等的情况下两圆能够完全重合
2、在一片草地上的A、B两处拴了一匹马和一只羊，其中拴羊的绳子长4米，拴马的绳子长7米，如图所示，请你画出马和羊都可以吃到草的区域。 (假设A、B之间相距10米)
A
B
C
D
M
N
圆上任意两点间
的部分叫做圆弧,
简称弧.大于半圆的弧称为优弧，小于半圆的弧称为劣弧
连接圆上任意两点
间的线段叫做弦
(如弦CD)
概念明晰
直径是最长的弦
1、请写出图中所有的弦；
2、请在图中任选一条弦，写出这条弦所对的弧；
认识弦与弧
A
B
C
O
E
3、判断
（1）圆是一条封闭曲线，它上面的任何一点到某个定点的距离都等于定长。（ ）
（2）圆的任何一条弦的两端点，把圆分成两条 弧，所以一条弦对两条弧。（ ）
（3）到圆心的距离小于半径的点在圆上。（ ）
（4）直径是弦，且圆内最长的弦是直径。（ ）
（5）半圆是弧，弧小于半圆。（ ）
（6）圆上的任意两点都能将圆分成一条劣弧
和一条优弧。（ ）
√
×
√
√
√
×
爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们以一面表面比较平整的土墙上为靶子，规则是谁掷出落点离O越近，谁就胜。如下图中是他们三人某一轮掷镖的落点，你认为这一轮中谁的成绩最好？
猜一猜
小兵
小强
小华
O
B
A
C
点A、B、C与圆的位置如图所示，设⊙O的半径为r，点到圆心的距离为d，则d和r 的大小关系为：
d＝r
d＞r
d＜r
点与圆的位置关系
O
点A在圆上
点B在圆内
点C在圆外
r
1、已知⊙O的面积为25π。
（1）若PO=5.5，则点P在 ；
（2）若PO=4，则点P在 ；
（3）若PO= ，则点P在圆上。
圆外
圆内
5
课内练习
2、在Rt △ ABC中，∠C=Rt∠，AC=3cm，AB=5cm。若以点C为圆心，画一个半径为3cm的圆，试判断点A，点B和⊙C的相互位置关系。
C
A
B
3cm
5cm
4cm
3、在以AB=5cm 为直径的圆上，到直线AB的距离为2.5cm的点有（ ）
A、无数个 B、1个 C、2个 D、4个
C
C
若圆P的半径为12呢？
4、若⊙P的半径长为13cm,
圆心P的坐标为（5、12），
则平面直角坐标系的原点O与⊙ P
位置关系是（ ）
A、在圆内 B、在圆外
C、在圆上 D、无法确定
5、如图，在△ABC中∠BAC=Rt∠，AO是BC边上的中线，
BC为⊙O的直径。
问：点A是否在圆上？请说明理由；
A
C
B
O
如图所示，在A地正北80m的Ｂ处有一幢民房，正西100m的C处有一变电设施，在BC的中点D处是一古建筑。
因施工需要，必须在A处进行一次爆破。为使民房、变电设施、古建筑都不遭到破坏，问爆破影响面的半径应控制在什么范围内？
课外拓展
⊙O的半径为2，点P到圆心
的距离OP=m，且m使关于x
的方程2x2-2√2x+m-1=0有
实根，试确定点P位置。
一