2020-2021学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 21:17:49 | ||
图片预览




文档简介
2020-2021学年浙教新版八年级上册数学《第1章
三角形的初步认识》单元测试卷
一.选择题
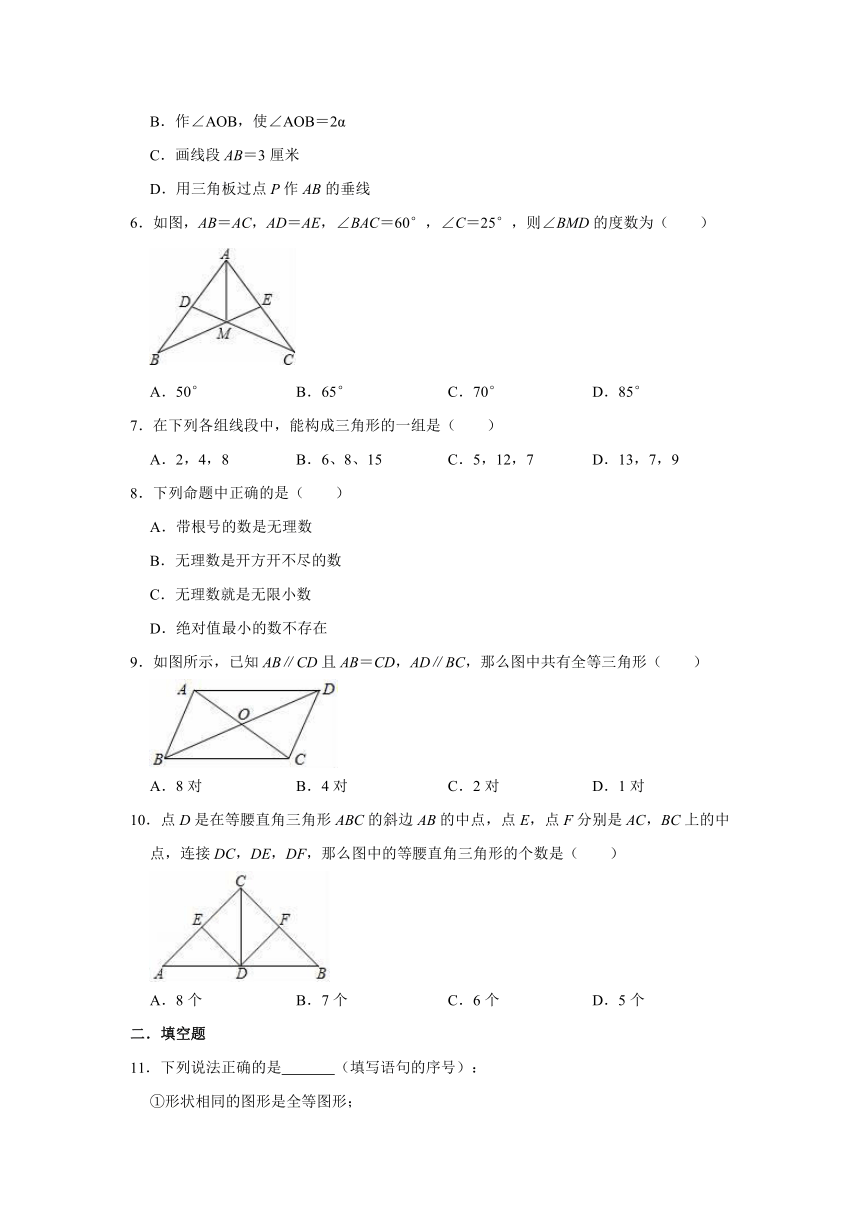
1.如图在△ABC中,∠ACB>90°,AD⊥BD,BE⊥AE,CF⊥AB,垂足分别是点D、E、F,则下列说法错误的是( )
A.AD是△ABD的高
B.CF是△ABC的高
C.BE是△ABC的高
D.BC是△BCF的高
2.如图.小王爸爸用四根木条钉成一个平行四边形木架,要使木架不变形,他至少要钉上木条的根数为( )
A.0
根
B.1根
C.2根
D.3根
3.用锯锯木,锯会发热;用锉锉物,锉会发热;在石头上磨刀,刀会发热,所以物体摩擦会发热.此结论的得出运用的方法是( )
A.观察
B.实验
C.归纳
D.类比
4.如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
A.20°
B.30°
C.35°
D.40°
5.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
6.如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
A.50°
B.65°
C.70°
D.85°
7.在下列各组线段中,能构成三角形的一组是( )
A.2,4,8
B.6、8、15
C.5,12,7
D.13,7,9
8.下列命题中正确的是( )
A.带根号的数是无理数
B.无理数是开方开不尽的数
C.无理数就是无限小数
D.绝对值最小的数不存在
9.如图所示,已知AB∥CD且AB=CD,AD∥BC,那么图中共有全等三角形( )
A.8对
B.4对
C.2对
D.1对
10.点D是在等腰直角三角形ABC的斜边AB的中点,点E,点F分别是AC,BC上的中点,连接DC,DE,DF,那么图中的等腰直角三角形的个数是( )
A.8个
B.7个
C.6个
D.5个
二.填空题
11.下列说法正确的是
(填写语句的序号):
①形状相同的图形是全等图形;
②边长相等的等边三角形是全等图形;
③面积相等的三角形是全等三角形;
④平移前后的两个图形一定是全等形;
⑤全等图形的对应边和对应角都相等.
12.如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,则∠B的对应角是
.
13.如图:(1)AD⊥BC,垂足为D,则AD是
的高,∠
=∠
=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫
,∠
=∠
=∠
,AH叫
;
(3)若AF=FC,则△ABC的中线是
;
(4)若BG=GH=HF,则AG是
的中线,AH是
的中线.
14.三条线段a=6,b=3,c为整数,由a,b,c为边组成的三角形共有
个.
15.如图,小明要测量河岸相对的两点A,B的距离,他先在AB的垂线BF上取两点C,D,使CD=BC,再过点D作BF的垂线DE,使A,C,E三点在同一条直线上.你认为此时测量
的长度就等于AB的长,理由是依据
,可以证明
,由全等三角形对应边相等得出.
16.已知线段a、b和直角α,作△ABC,使∠C=90°,CB=a,CA=b.
(1)作∠MCN=90°.
(2)以C为圆心,以
为半径画弧,交CM于B.
(3)以
为圆心,以
为半径,画弧交CN于A.
(4)连结
得到△ABC.
17.如图,对面积为a的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1,B1,C1,使得A1B=2AB,B1C=2BC,C1A=2AC,顺次连接A1,B1,C1,得△A1B1C1,则其面积S=
(用含a的式子表示).
18.如图所示,△ABC的高CE,BD相交于点H,若∠A=60°,则∠DHE=
.∠HBE=
.
19.在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于点F,则下列说法中正确的是
.
①∠BOE=60°;②∠ABD=∠ACE;③OE=OD.
20.用1个6,1个8,2个9可组成多种不同的四位数,这些四位数共有
个.
三.解答题
21.已知点C,D分别在∠AOB的边OB,OA上,按下列要求画图.(作图时,可先使用2B铅笔,确定后必须使用0.5毫米及以上的黑色签字笔涂黑)
(1)画直线CD;
(2)过点C画射线OA的垂直线段CE,垂足为E;
(3)若CE平分∠DCO,∠AOB=30°,求∠DCB的度数.
22.已知,如图所示,AC,BD相交于点O,BP,CP分别平分∠ABD,∠ACD,且相交于点P,试探究∠P与∠A,∠D之间的数量关系.
23.在一次测试中,老师出了如下题目:比较nn+1与(n+1)n的大小.有些同学经过计算发现:当n=1、2时,nn+1<(n+1)n,于是认为命题“如果n为任意自然数,则nn+1<(n+1)n”为真命题.你认为他们的判断正确吗?说说你的理由.
24.如图,△ADE≌△CBF,AD=BC,求证:AE∥CF.
25.阅读理解题:如图:已知AC,BD相交于O,OA=OB,OC=OD.
那么△ABC与△BAD全等吗?请说明理由.
小明的解答:
而△BAD=△AOD+△ADB,△ABC=△BOC+△AOB,所以△ABC≌△BAD.
(1)你认为小明的解答有无错误;
(2)如有错误给出正确解答.
26.小华每天起床后要做的事情有穿衣(4min)、整理床(3min)、洗脸梳头(5min)、上厕所
(5min)、烧饭(20min)、吃早饭(12min),完成这些工作共需49min,你认为最合理的安排应是多少分钟?
参考答案与试题解析
一.选择题
1.解:A、AD是△ABD的高正确,故本选项错误;
B、CF是△ABC的高正确,故本选项错误;
C、BE是△ABC的高正确,故本选项错误;
D、BC是△BCF的高错误,故本选项正确.
故选:D.
2.解:如图,添加一根木条把四边形分成两个三角形即可.
故选:B.
3.解:由多种现象得到一个规律属于归纳.故选C.
4.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB,
∴∠A′CB′﹣∠A′CB=∠ACB﹣∠A′CB,
∴∠B′CB=∠ACA′,
∵∠A′CB′=65°,∠A′CB=35°,
∴∠ACA′=∠BCB′=∠A′CB′﹣∠A′CB=65°﹣35°=30°,
故选:B.
5.解:根据尺规作图的定义可得:B属于尺规作图,
故选:B.
6.证明:∵∠BAC=60°,∠C=25°,
∴∠BDC=25°+60°=85°,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C=25°,
∴∠DNB=180°﹣25°﹣85°=70°,
故选:C.
7.解:A、∵2+4<8,∴无法构成三角形,不合题意;
B、∵6+8<15,∴无法构成三角形,不合题意;
C、∵5+7=12,∴无法构成三角形,不合题意;
D、∵7+9>13,∴可以构成三角形,符合题意;
故选:D.
8.解:∵,故选项A错误;
无理数不一定是开放开不尽的数,如π是无理数,故选项B错误;
无理数就是无限小数,故选项C正确;
绝对值最小的数是0,故选项D错误;
故选:C.
9.解:全等三角形有△ABD≌△CDB,△ACD≌△CAB,△AOD≌△COB,△AOB≌△COD,共4对,
故选:B.
10.解:∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=AD=DB,
∴△ADC,△CDB都是等腰直角三角形,
∵DA=DC,∠ADC=90°,AE=EC,
∴DE=AE=EC,
∴△AEC,△DEC都是等腰三角形,
同法可证△CDF,△DFB都是等腰三角形,
∴△ABC,△ADC,△CDB,△AED,△DEC,△CDF,△DFB都是等腰三角形,
故选:B.
二.填空题
11.解:①形状相同,大小相等的图形是全等图形,故本小题错误;
②边长相等的等边三角形是全等图形,正确;
③面积相等的三角形是全等三角形,错误;
④平移前后的两个图形一定是全等形,正确;
⑤全等图形的对应边和对应角都相等,正确.
所以,正确的说法有②④⑤.
故答案为:②④⑤.
12.解:∵△ABC≌△CDA,
∴∠B=∠D,
故答案为:∠D.
13.解:(1)AD⊥BC,垂足为D,则AD是BC边上的高,∠ADB=∠ADC=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线,∠BAE=∠CAE=∠BAC,AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线,AH是△AGF的中线.
故答案为(1)BC边上,ADB,ADC;(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;(3)BF;(4)△ABH,△AGF.
14.解:根据三角形的三边关系知c的取值范围是:3<c<9,
又c的值为整数,
因而c的值可以是:4、5、6、7、8共5个数,
因而由a、b、c为边可组成5个三角形.
故答案为:5.
15.解:∵在△ABC和△EDC中
,
∴△ABC≌△EDC(ASA),
故AB=DE,
即此时测量DE的长度就等于AB的长,
故答案为:DE,全等三角形,对应边相等,△ABC≌△EDC.
16.解:如图所示:
(1)作∠MCN=90°.
(2)以C为圆心,以a为半径画弧,交CM于B.
(3)以点C为圆心,以b为半径,画弧交CN于A.
(4)连结
AB得到△ABC.
故答案为:a,点C,b,AB.
17.解:连接BC1,
∵C1A=2CA,
∴S△ABC1=2S△ABC,
同理:S△A1BC1=2S△ABC1=4S△ABC,
∴S△A1AC1=6S△ABC,
同理:S△A1BB1=S△CB1C1=6S△ABC,
∴S△A1B1C1=19S△ABC=19a,
故答案为19a.
18.解:∵△ABC的高CE,BD相交于点H,
∴∠ADB=∠BEH=90°,
∴∠HBE+∠A=90°,
∴∠HBE=90°﹣60°=30°,
∴∠DHE=∠BEH+∠HBE=90°+30°=120°;
故答案为:120°,30°.
19.解:①如图,∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠OBC+∠OCB=×120°=60°,
∴∠BOE=∠OBC+∠OCB=60°,故①正确;
②∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠ABD=∠ABC,∠ACE=∠ACB,
当AB=AC时,∠ABC=∠ACB,
而已知AB和AC没有相等关系,故②不正确;
③∵∠OBC+∠OCB=60°,
∴∠BOC=120°,
∵OF平分∠BOC,
∴∠BOF=∠COF=60°,
∴∠BOE=60°,
∴∠BOE=∠BOF,
在△BOE和△BOF中,
,
∴△BOE≌△BOF(ASA),
∴OE=OF,
同理得:△CDO≌△CFO,
∴OD=OF,
∴OD=OE,故③正确;
故答案为:①③.
20.解:由题意,这个四位数可以是6899,6989,6998,8699,8969,8996,9869,9689,9698,9896,9986,9968.因此共有12个.
三.解答题
21.解:(1)如图所示,直线CD即为所求;
(2)如图所示,线段CE即为所求;
(3)∵CE⊥OD,
∴∠CEO=∠CED,
∵CE平分∠DCO,
∴∠OCE=∠DCE,
∴∠AOB=∠CDO=30°,
∵∠DCB=∠AOB+∠CDO=60°.
22.解:∵∠CFB=∠A+∠ABF,∠CFB=∠P+∠PCF(三角形的外角等于两个不相邻的内角的和),
∴∠A+∠ABF=∠P+∠PCF(等量代换),
同理:∠D+∠DCP=∠P+∠DBP,
∴∠A+∠ABF+∠D+∠DCP=2∠P+∠PCF+∠DBP(等式性质),
∵CP,BP分别平分∠DCA,∠DBA,
∴∠ABF=∠DBP,∠DCP=∠PCF(角平分线的定义),
∴∠A+∠D=2∠P;
∴∠P=(∠A+∠D).
23.解:他们的判断不正确.理由如下:
当n=3时,nn+1=34=81,(n+1)n=43=64,则nn+1>(n+1)n.
24.解:∵△ADE≌△CBF,AD=BC,
∴∠AED=∠F,
∴AE∥CF.
25.解:(1)小明的解答有错误;
(2)正确解答如下:
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴∠ADO=∠BCO,DA=CB,
∴∠ADB=∠BCA,
∵OA=OB,OC=OD,
∴DB=CA,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
26.解:时间安排如下:
穿衣以后先烧饭,在这同时完成整理床铺,洗脸梳头,上厕所;最后吃早饭.
用时:4+20+12=36(分钟)
答:最合理的安排只需要36分钟.
三角形的初步认识》单元测试卷
一.选择题
1.如图在△ABC中,∠ACB>90°,AD⊥BD,BE⊥AE,CF⊥AB,垂足分别是点D、E、F,则下列说法错误的是( )
A.AD是△ABD的高
B.CF是△ABC的高
C.BE是△ABC的高
D.BC是△BCF的高
2.如图.小王爸爸用四根木条钉成一个平行四边形木架,要使木架不变形,他至少要钉上木条的根数为( )
A.0
根
B.1根
C.2根
D.3根
3.用锯锯木,锯会发热;用锉锉物,锉会发热;在石头上磨刀,刀会发热,所以物体摩擦会发热.此结论的得出运用的方法是( )
A.观察
B.实验
C.归纳
D.类比
4.如图,△ACB≌△A′CB′,∠A′CB′=65°,∠A′CB=35°,则∠ACA′的度数( )
A.20°
B.30°
C.35°
D.40°
5.下列作图属于尺规作图的是( )
A.用量角器画出∠AOB的平分线OC
B.作∠AOB,使∠AOB=2α
C.画线段AB=3厘米
D.用三角板过点P作AB的垂线
6.如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
A.50°
B.65°
C.70°
D.85°
7.在下列各组线段中,能构成三角形的一组是( )
A.2,4,8
B.6、8、15
C.5,12,7
D.13,7,9
8.下列命题中正确的是( )
A.带根号的数是无理数
B.无理数是开方开不尽的数
C.无理数就是无限小数
D.绝对值最小的数不存在
9.如图所示,已知AB∥CD且AB=CD,AD∥BC,那么图中共有全等三角形( )
A.8对
B.4对
C.2对
D.1对
10.点D是在等腰直角三角形ABC的斜边AB的中点,点E,点F分别是AC,BC上的中点,连接DC,DE,DF,那么图中的等腰直角三角形的个数是( )
A.8个
B.7个
C.6个
D.5个
二.填空题
11.下列说法正确的是
(填写语句的序号):
①形状相同的图形是全等图形;
②边长相等的等边三角形是全等图形;
③面积相等的三角形是全等三角形;
④平移前后的两个图形一定是全等形;
⑤全等图形的对应边和对应角都相等.
12.如图,△ABC≌△CDA,AB和CD,BC和DA是对应边,则∠B的对应角是
.
13.如图:(1)AD⊥BC,垂足为D,则AD是
的高,∠
=∠
=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫
,∠
=∠
=∠
,AH叫
;
(3)若AF=FC,则△ABC的中线是
;
(4)若BG=GH=HF,则AG是
的中线,AH是
的中线.
14.三条线段a=6,b=3,c为整数,由a,b,c为边组成的三角形共有
个.
15.如图,小明要测量河岸相对的两点A,B的距离,他先在AB的垂线BF上取两点C,D,使CD=BC,再过点D作BF的垂线DE,使A,C,E三点在同一条直线上.你认为此时测量
的长度就等于AB的长,理由是依据
,可以证明
,由全等三角形对应边相等得出.
16.已知线段a、b和直角α,作△ABC,使∠C=90°,CB=a,CA=b.
(1)作∠MCN=90°.
(2)以C为圆心,以
为半径画弧,交CM于B.
(3)以
为圆心,以
为半径,画弧交CN于A.
(4)连结
得到△ABC.
17.如图,对面积为a的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1,B1,C1,使得A1B=2AB,B1C=2BC,C1A=2AC,顺次连接A1,B1,C1,得△A1B1C1,则其面积S=
(用含a的式子表示).
18.如图所示,△ABC的高CE,BD相交于点H,若∠A=60°,则∠DHE=
.∠HBE=
.
19.在△ABC中,已知∠A=60°,∠ABC的平分线BD与∠ACB的平分线CE相交于点O,∠BOC的平分线交BC于点F,则下列说法中正确的是
.
①∠BOE=60°;②∠ABD=∠ACE;③OE=OD.
20.用1个6,1个8,2个9可组成多种不同的四位数,这些四位数共有
个.
三.解答题
21.已知点C,D分别在∠AOB的边OB,OA上,按下列要求画图.(作图时,可先使用2B铅笔,确定后必须使用0.5毫米及以上的黑色签字笔涂黑)
(1)画直线CD;
(2)过点C画射线OA的垂直线段CE,垂足为E;
(3)若CE平分∠DCO,∠AOB=30°,求∠DCB的度数.
22.已知,如图所示,AC,BD相交于点O,BP,CP分别平分∠ABD,∠ACD,且相交于点P,试探究∠P与∠A,∠D之间的数量关系.
23.在一次测试中,老师出了如下题目:比较nn+1与(n+1)n的大小.有些同学经过计算发现:当n=1、2时,nn+1<(n+1)n,于是认为命题“如果n为任意自然数,则nn+1<(n+1)n”为真命题.你认为他们的判断正确吗?说说你的理由.
24.如图,△ADE≌△CBF,AD=BC,求证:AE∥CF.
25.阅读理解题:如图:已知AC,BD相交于O,OA=OB,OC=OD.
那么△ABC与△BAD全等吗?请说明理由.
小明的解答:
而△BAD=△AOD+△ADB,△ABC=△BOC+△AOB,所以△ABC≌△BAD.
(1)你认为小明的解答有无错误;
(2)如有错误给出正确解答.
26.小华每天起床后要做的事情有穿衣(4min)、整理床(3min)、洗脸梳头(5min)、上厕所
(5min)、烧饭(20min)、吃早饭(12min),完成这些工作共需49min,你认为最合理的安排应是多少分钟?
参考答案与试题解析
一.选择题
1.解:A、AD是△ABD的高正确,故本选项错误;
B、CF是△ABC的高正确,故本选项错误;
C、BE是△ABC的高正确,故本选项错误;
D、BC是△BCF的高错误,故本选项正确.
故选:D.
2.解:如图,添加一根木条把四边形分成两个三角形即可.
故选:B.
3.解:由多种现象得到一个规律属于归纳.故选C.
4.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB,
∴∠A′CB′﹣∠A′CB=∠ACB﹣∠A′CB,
∴∠B′CB=∠ACA′,
∵∠A′CB′=65°,∠A′CB=35°,
∴∠ACA′=∠BCB′=∠A′CB′﹣∠A′CB=65°﹣35°=30°,
故选:B.
5.解:根据尺规作图的定义可得:B属于尺规作图,
故选:B.
6.证明:∵∠BAC=60°,∠C=25°,
∴∠BDC=25°+60°=85°,
在△AEB和△ADC中,
,
∴△AEB≌△ADC(SAS),
∴∠B=∠C=25°,
∴∠DNB=180°﹣25°﹣85°=70°,
故选:C.
7.解:A、∵2+4<8,∴无法构成三角形,不合题意;
B、∵6+8<15,∴无法构成三角形,不合题意;
C、∵5+7=12,∴无法构成三角形,不合题意;
D、∵7+9>13,∴可以构成三角形,符合题意;
故选:D.
8.解:∵,故选项A错误;
无理数不一定是开放开不尽的数,如π是无理数,故选项B错误;
无理数就是无限小数,故选项C正确;
绝对值最小的数是0,故选项D错误;
故选:C.
9.解:全等三角形有△ABD≌△CDB,△ACD≌△CAB,△AOD≌△COB,△AOB≌△COD,共4对,
故选:B.
10.解:∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,CD=AD=DB,
∴△ADC,△CDB都是等腰直角三角形,
∵DA=DC,∠ADC=90°,AE=EC,
∴DE=AE=EC,
∴△AEC,△DEC都是等腰三角形,
同法可证△CDF,△DFB都是等腰三角形,
∴△ABC,△ADC,△CDB,△AED,△DEC,△CDF,△DFB都是等腰三角形,
故选:B.
二.填空题
11.解:①形状相同,大小相等的图形是全等图形,故本小题错误;
②边长相等的等边三角形是全等图形,正确;
③面积相等的三角形是全等三角形,错误;
④平移前后的两个图形一定是全等形,正确;
⑤全等图形的对应边和对应角都相等,正确.
所以,正确的说法有②④⑤.
故答案为:②④⑤.
12.解:∵△ABC≌△CDA,
∴∠B=∠D,
故答案为:∠D.
13.解:(1)AD⊥BC,垂足为D,则AD是BC边上的高,∠ADB=∠ADC=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线,∠BAE=∠CAE=∠BAC,AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线,AH是△AGF的中线.
故答案为(1)BC边上,ADB,ADC;(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;(3)BF;(4)△ABH,△AGF.
14.解:根据三角形的三边关系知c的取值范围是:3<c<9,
又c的值为整数,
因而c的值可以是:4、5、6、7、8共5个数,
因而由a、b、c为边可组成5个三角形.
故答案为:5.
15.解:∵在△ABC和△EDC中
,
∴△ABC≌△EDC(ASA),
故AB=DE,
即此时测量DE的长度就等于AB的长,
故答案为:DE,全等三角形,对应边相等,△ABC≌△EDC.
16.解:如图所示:
(1)作∠MCN=90°.
(2)以C为圆心,以a为半径画弧,交CM于B.
(3)以点C为圆心,以b为半径,画弧交CN于A.
(4)连结
AB得到△ABC.
故答案为:a,点C,b,AB.
17.解:连接BC1,
∵C1A=2CA,
∴S△ABC1=2S△ABC,
同理:S△A1BC1=2S△ABC1=4S△ABC,
∴S△A1AC1=6S△ABC,
同理:S△A1BB1=S△CB1C1=6S△ABC,
∴S△A1B1C1=19S△ABC=19a,
故答案为19a.
18.解:∵△ABC的高CE,BD相交于点H,
∴∠ADB=∠BEH=90°,
∴∠HBE+∠A=90°,
∴∠HBE=90°﹣60°=30°,
∴∠DHE=∠BEH+∠HBE=90°+30°=120°;
故答案为:120°,30°.
19.解:①如图,∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠OBC+∠OCB=×120°=60°,
∴∠BOE=∠OBC+∠OCB=60°,故①正确;
②∵BD、CE分别是∠ABC和∠BCA的平分线,
∴∠ABD=∠ABC,∠ACE=∠ACB,
当AB=AC时,∠ABC=∠ACB,
而已知AB和AC没有相等关系,故②不正确;
③∵∠OBC+∠OCB=60°,
∴∠BOC=120°,
∵OF平分∠BOC,
∴∠BOF=∠COF=60°,
∴∠BOE=60°,
∴∠BOE=∠BOF,
在△BOE和△BOF中,
,
∴△BOE≌△BOF(ASA),
∴OE=OF,
同理得:△CDO≌△CFO,
∴OD=OF,
∴OD=OE,故③正确;
故答案为:①③.
20.解:由题意,这个四位数可以是6899,6989,6998,8699,8969,8996,9869,9689,9698,9896,9986,9968.因此共有12个.
三.解答题
21.解:(1)如图所示,直线CD即为所求;
(2)如图所示,线段CE即为所求;
(3)∵CE⊥OD,
∴∠CEO=∠CED,
∵CE平分∠DCO,
∴∠OCE=∠DCE,
∴∠AOB=∠CDO=30°,
∵∠DCB=∠AOB+∠CDO=60°.
22.解:∵∠CFB=∠A+∠ABF,∠CFB=∠P+∠PCF(三角形的外角等于两个不相邻的内角的和),
∴∠A+∠ABF=∠P+∠PCF(等量代换),
同理:∠D+∠DCP=∠P+∠DBP,
∴∠A+∠ABF+∠D+∠DCP=2∠P+∠PCF+∠DBP(等式性质),
∵CP,BP分别平分∠DCA,∠DBA,
∴∠ABF=∠DBP,∠DCP=∠PCF(角平分线的定义),
∴∠A+∠D=2∠P;
∴∠P=(∠A+∠D).
23.解:他们的判断不正确.理由如下:
当n=3时,nn+1=34=81,(n+1)n=43=64,则nn+1>(n+1)n.
24.解:∵△ADE≌△CBF,AD=BC,
∴∠AED=∠F,
∴AE∥CF.
25.解:(1)小明的解答有错误;
(2)正确解答如下:
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴∠ADO=∠BCO,DA=CB,
∴∠ADB=∠BCA,
∵OA=OB,OC=OD,
∴DB=CA,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
26.解:时间安排如下:
穿衣以后先烧饭,在这同时完成整理床铺,洗脸梳头,上厕所;最后吃早饭.
用时:4+20+12=36(分钟)
答:最合理的安排只需要36分钟.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
