有理数的大小比较

(共20张PPT)
请比较下列几组数的大小：
不忘老朋友

⑴ 0.6 ___ 0 ；　　
⑵ 2 ___ 7；
⑶ ___
<
>
<
1.5 有理数的大小比较
第一章 从自然数到有理数
下图表示某一天我国5个城市的最低气温.
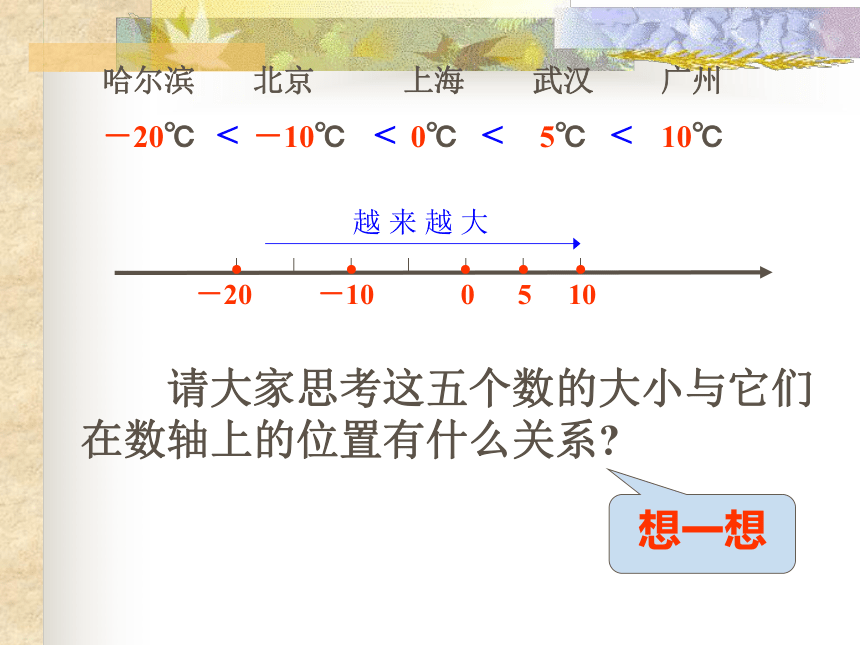
武汉5 ℃ 北京－10℃　上海0℃ 广州10℃ 哈尔滨－20℃
问：你能将上述五个城市的最低气温按从低到高的顺序依次排列吗？
哈尔滨
－20℃
北京
－10℃
上海
0℃
武汉
5℃
广州
10℃
说一说

<
<
<
<
请大家思考这五个数的大小与它们在数轴上的位置有什么关系
想一想
越 来 越 大
哈尔滨
－20℃
北京
－10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
－20 －10 0 5 10
●
●
●
●
●
记住了吗？
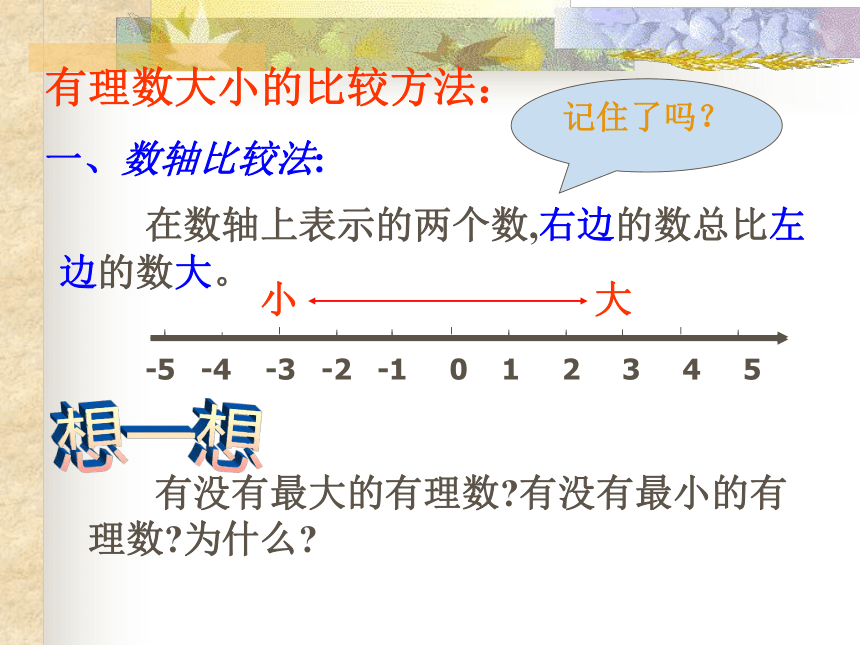
有理数大小的比较方法：
一、数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大。
-5 -4 -3 -2 -1 0 1 2 3 4 5
小 大
有没有最大的有理数 有没有最小的有理数 为什么
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
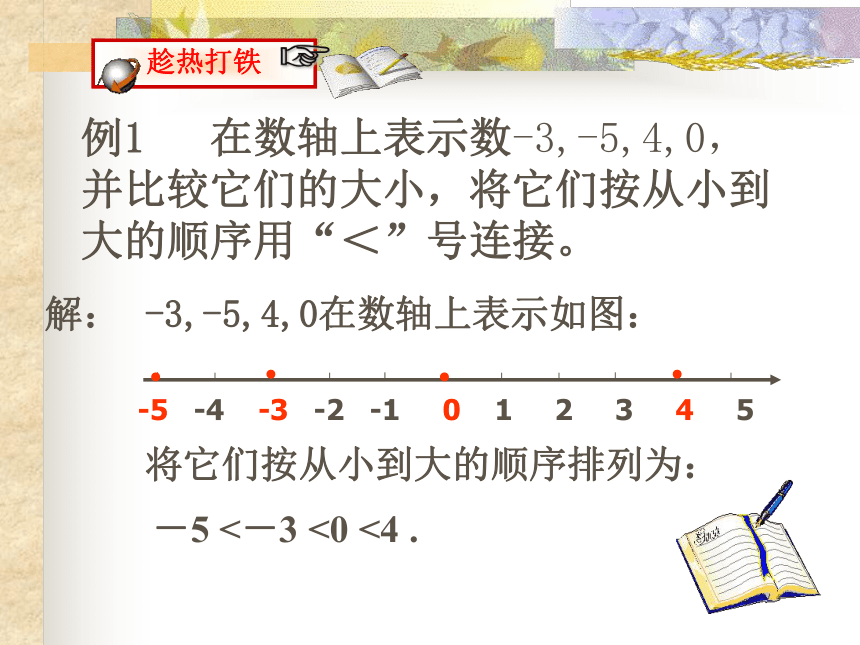
趁热打铁

例1 在数轴上表示数-3,-5,4,0，并比较它们的大小，将它们按从小到大的顺序用“＜”号连接。
解：
-3,-5,4,0在数轴上表示如图：
将它们按从小到大的顺序排列为：
－5 <－3 <0 <4 .
把下列各数表示在数轴上，并按从小到大的顺序用“ < ”号连接：
5，0， －4　，－2，
你会了吗？
模仿练习
(1) 比较-3,-5的大小;
(2)求这两个数的绝对值，并比较大小；
(3)负数的大小与它们的绝对值的大小的关系。
两个负数比较大小，绝对值
大的反而小。
都记住了吗？
有理数大小的比较方法：
一、数轴比较法:
1、 正数都大于零，负数都小于零，
正数大于一切负数。
2、两个正数比较大小，
两个负数比较大小，绝对值大的数反而小。
二、直接比较法：
绝对值大的数大；
在数轴上表示的两个数,右边的数总比左边的数大。
|
|
|
|
|
|
|
|
|
-5 -4 -3 -2 -1 0 1 2 3
例2 比较下列每对数的大小，并说明理由：
⑴　1与－ 10；　 ⑵－ 0.001与0
⑶ － 9与－11 ⑷－ 　与－
解：
⑴1>－10
（正数大于一切负数）
⑵－0.001<0
（负数都小于零）
灵活运用

　比较下面各对数的大小，并说明理由：
⑴　　____　　； ⑵－3 ____+1；
⑶ －1 ____0； ⑷ －　___－　 ；
⑸ －|－3| ____－4.5
>
<
<
<
>
巩固知识

2、填空：绝对值最小的有理数是 ；绝对值最小的自然数是 ；绝对值最小的负整数是 。
0
0
－1
好好想想
1、利用数轴回答： ⑴有没有最大的整数和最小的整数？
⑶有没有最大的负整数和最小的负整数？
答：没有最大的正整数，最小的正整数是1。
答：都没有。
⑵有没有最大的正整数和最小的正整数？
答：最大的负整数是－1，没有最小的负整数。
4、你能写出绝对值不大于2的所有整数吗？
3、求大于－ 4并且小于3.2的所有整数。
答：大于－ 4并且小于3.2的整数有：
－3，－2，－1，0，1，2，3.
答：绝对值不大于2的整数有：－2，－1，0，1，2.
合作探究

（2）若a>0，b<0，且|a|<|b|，则你能比较a、b、－a、－b这四个数的大小吗？
（1）小明在课外书上看到一道习题：“若a表示一个有理数，请比较a与－a的大小”，他觉得太简单了，马上就得出了a> －a的结论，他做得对吗？
挑战自我
分类讨论：
若a是正数，则a>－a；
若a是负数，则a<－a；
若a是零，则a＝--a。
答：b<－a < a <－b
1、有理数的大小比较有两种方法：数轴比较法和直接比较法。
2、你觉得什么情况下运用直接比较法简单，什么情况下利用数轴比较法简单？说说你的想法？
小结 拓展
别忘了 作业
若|a|=-a, |b|=b, |c|=-c, |d|=-d,且无一个数为零，还满足|a|>|b|>|c|>|d|,请把a,b,c,d四个数从小到大排列。
同学们再见！
谢 谢