2.3二次函数的性质 (1)师生共用讲学稿
文档属性
| 名称 | 2.3二次函数的性质 (1)师生共用讲学稿 |
|
|
| 格式 | zip | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-20 00:00:00 | ||
图片预览

文档简介
师生共用讲学稿
年级:九年级(上) 学科:数学 设计:顾老师
内容:2.3二次函数的性质 (1) 课型:新授 时间:2011年7月23日
复习引入
二次函数: y=ax2 +bx + c (a 0)的图象是一条抛物线,它的开口由什么决定呢
二,新课教学:
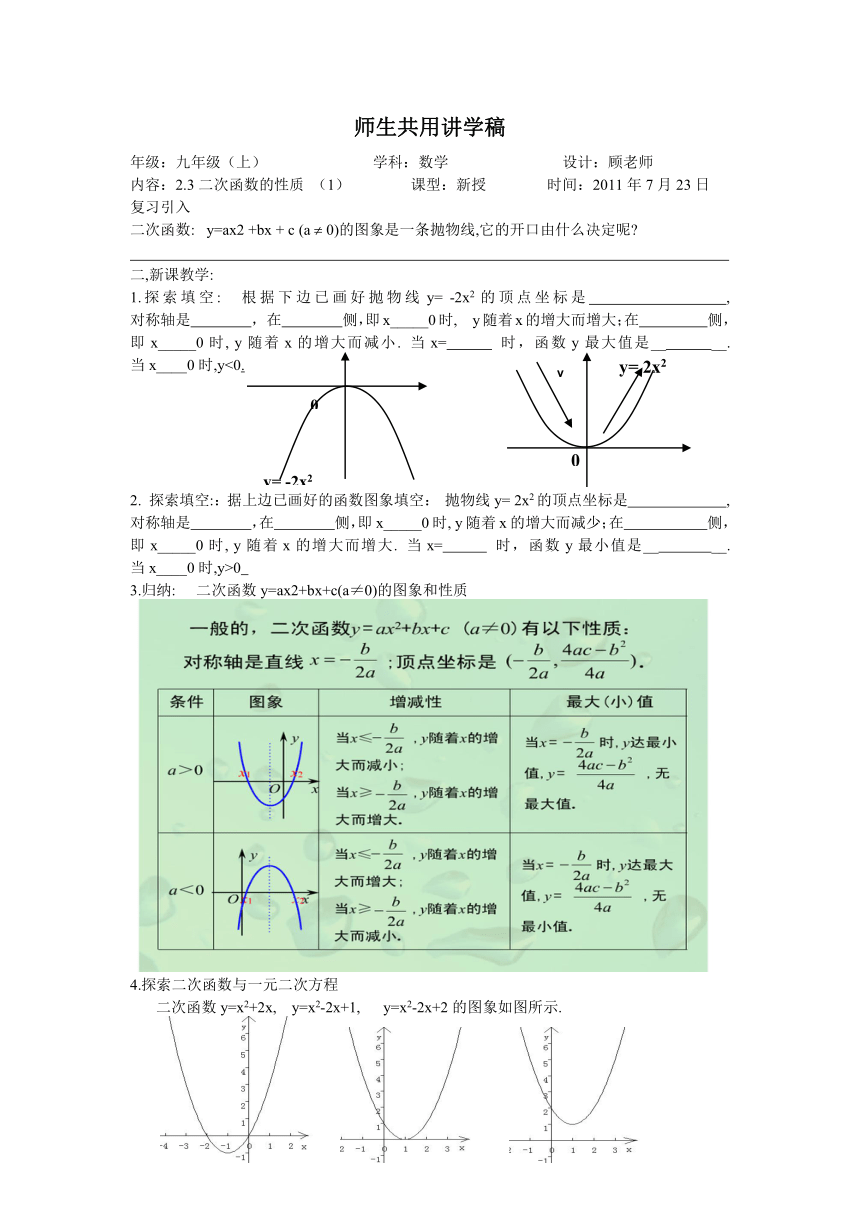
1.探索填空: 根据下边已画好抛物线y= -2x2的顶点坐标是 , 对称轴是 , 在 侧,即x_____0时, y随着x的增大而增大;在 侧,即x_____0时, y随着x的增大而减小. 当x= 时,函数y最大值是__ __. 当x____0时,y<0.
2. 探索填空::据上边已画好的函数图象填空: 抛物线y= 2x2的顶点坐标是 , 对称轴是 ,在 侧,即x_____0时, y随着x的增大而减少;在 侧,即x_____0时, y随着x的增大而增大. 当x= 时,函数y最小值是__ __. 当x____0时,y>0
3.归纳: 二次函数y=ax2+bx+c(a≠0)的图象和性质
4.探索二次函数与一元二次方程
二次函数y=x2+2x, y=x2-2x+1, y=x2-2x+2的图象如图所示.
(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0, x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
归纳:.二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点, ②有一个交点, ③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时, 交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
当b2-4ac﹥0时,抛物线与x轴有两个交点,交点的横坐标是一元二次方程0=ax2+bx+c的两个根x1与 x2;当b2-4ac=0时,抛物线与x轴有且只有一个公共点;当b2-4ac﹤0时,抛物线与x轴没有交点。
例:已知函数
求函数图像的顶点坐标、对称轴,以及图像和坐标轴的交点坐标,并画出函数的大致图像。
自变量x在什么范围内时,y随x的增大而增大?何时y随x增大而减小?并求出函数的最大值或最小值?
练习1、已知函数: 1、 y=-x2+3x 2、 y=3x2-2x+1 3、 y=x2-2x+1
(1)求一、二两个函数的最大值(或最小值)和对应自变量的值。
(2)它们与x轴是否有交点,若有求出图象与x轴的交点坐标。
练习2、已知(-1,y1), (-2,y2), (-4,y3)是抛物线 y=-2x2-8x +6上的点,则 ( )
(A) y1<y2 < y3 (B) y3 < y2 < y1 (C) y2>y1 > y3 (D) y2 > y3 > y1
思考:(1)若把抛物线改为y=-2x2-8x +m,结果会如何呢?
(2)若把抛物线改为y=-2ax2-8ax +m,结果又会如何呢?
练习3、已知抛物线y=ax2经过点(-2,2).
(1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值.
(3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
练习4、已知函数y= x2 -2x -3
(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图;
(2)求图象与坐标轴交点构成的三角形的面积:
(3)根据第(1)题的图象草图,说 出 x 取哪些值时,① y=0; ② y<0; ③ y>0.
0
y= -2x2
y= 2x2
0
y
x
年级:九年级(上) 学科:数学 设计:顾老师
内容:2.3二次函数的性质 (1) 课型:新授 时间:2011年7月23日
复习引入
二次函数: y=ax2 +bx + c (a 0)的图象是一条抛物线,它的开口由什么决定呢
二,新课教学:
1.探索填空: 根据下边已画好抛物线y= -2x2的顶点坐标是 , 对称轴是 , 在 侧,即x_____0时, y随着x的增大而增大;在 侧,即x_____0时, y随着x的增大而减小. 当x= 时,函数y最大值是__ __. 当x____0时,y<0.
2. 探索填空::据上边已画好的函数图象填空: 抛物线y= 2x2的顶点坐标是 , 对称轴是 ,在 侧,即x_____0时, y随着x的增大而减少;在 侧,即x_____0时, y随着x的增大而增大. 当x= 时,函数y最小值是__ __. 当x____0时,y>0
3.归纳: 二次函数y=ax2+bx+c(a≠0)的图象和性质
4.探索二次函数与一元二次方程
二次函数y=x2+2x, y=x2-2x+1, y=x2-2x+2的图象如图所示.
(1).每个图象与x轴有几个交点?
(2).一元二次方程x2+2x=0, x2-2x+1=0有几个根 验证一下一元二次方程x2-2x+2=0有根吗
(3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系
归纳:.二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点, ②有一个交点, ③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时, 交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
当b2-4ac﹥0时,抛物线与x轴有两个交点,交点的横坐标是一元二次方程0=ax2+bx+c的两个根x1与 x2;当b2-4ac=0时,抛物线与x轴有且只有一个公共点;当b2-4ac﹤0时,抛物线与x轴没有交点。
例:已知函数
求函数图像的顶点坐标、对称轴,以及图像和坐标轴的交点坐标,并画出函数的大致图像。
自变量x在什么范围内时,y随x的增大而增大?何时y随x增大而减小?并求出函数的最大值或最小值?
练习1、已知函数: 1、 y=-x2+3x 2、 y=3x2-2x+1 3、 y=x2-2x+1
(1)求一、二两个函数的最大值(或最小值)和对应自变量的值。
(2)它们与x轴是否有交点,若有求出图象与x轴的交点坐标。
练习2、已知(-1,y1), (-2,y2), (-4,y3)是抛物线 y=-2x2-8x +6上的点,则 ( )
(A) y1<y2 < y3 (B) y3 < y2 < y1 (C) y2>y1 > y3 (D) y2 > y3 > y1
思考:(1)若把抛物线改为y=-2x2-8x +m,结果会如何呢?
(2)若把抛物线改为y=-2ax2-8ax +m,结果又会如何呢?
练习3、已知抛物线y=ax2经过点(-2,2).
(1)求这条抛物线的解析式. (2)求出这个二次函数的最大值或最小值.
(3)在此抛物线上有两点A(x1,y1),B(x2,y2),且x1>x2>0,试比较y1与y2的大小.
练习4、已知函数y= x2 -2x -3
(1)写出函数图象的顶点、图象与坐标轴的交点,以及图象与 y 轴的交点关于图象对称轴的对称点。然后画出函数图象的草图;
(2)求图象与坐标轴交点构成的三角形的面积:
(3)根据第(1)题的图象草图,说 出 x 取哪些值时,① y=0; ② y<0; ③ y>0.
0
y= -2x2
y= 2x2
0
y
x
同课章节目录
