2020-2021学年浙教版八年级上册5.4 一次函数的图象与性质专题培优(Word版 附答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级上册5.4 一次函数的图象与性质专题培优(Word版 附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-12 00:00:00 | ||
图片预览


文档简介
2020-2021学年浙教版八年级上册一次函数的图象与性质专题培优
姓名
班级
学号
基础巩固
1.若点(m,n)在函数y
=
2x
+
1的图象上,则2
m
-
n的值是( ).
A.2
B.-
2
C.1
D.-1
2.在一次函数y
=
ax
-
a中,y随x的增大而减小,则其图象可能是( ).
3.若点M(-
7,m),N(-
8,n)都在函数y
=-(k2
+
2k
+
4)x
+
1(k为常数)的图象上,则m和n的大小关系是( ).
A.m
>
n
B.m
<
n
C.m
=
n
D.不能确定
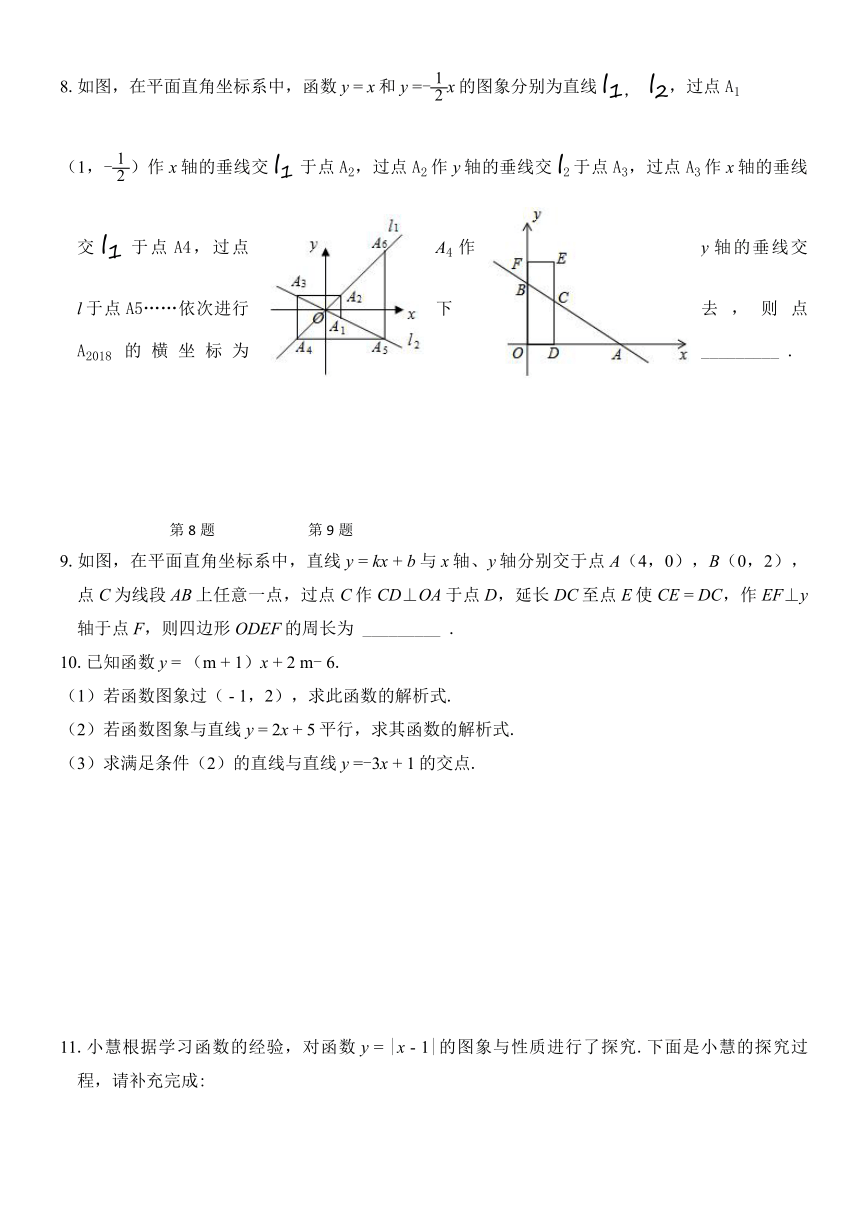
4.如图,已知直线l:y
=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点
A2…按此作法继续下去,则点A4的坐标为( ).
A.(0,64)
B.(0,128)
C.(0,256)
D.(0,512)
5.如图,已知A(5,0),直线y
=
x
+
b(b
>
0)与y轴交于点B,连结AB,∠=
75°,则b的值为( ).
A.3
B.
C.4
D.
6.直线y
=
2x
+
6与两坐标轴围成的三角形面积是
_________
.
7.如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y
=-x上,则点B与其对应点B′间的距离为
_________
.
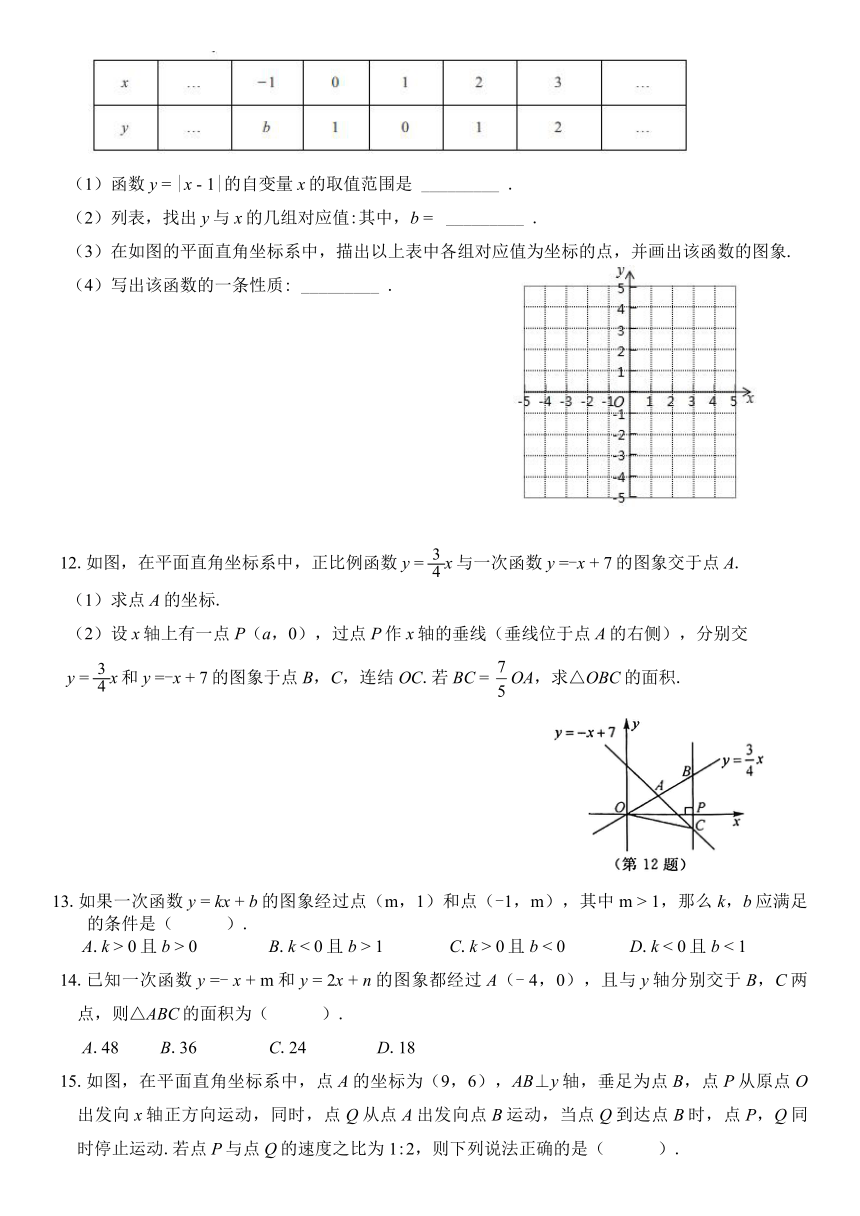
8.如图,在平面直角坐标系中,函数y
=
x和y
=-x的图象分别为直线l1,
l2,过点A1
(1,-)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l于点A5……依次进行下去,则点A2018的横坐标为
_________
.
第8题
第9题
9.如图,在平面直角坐标系中,直线y
=
kx
+
b与x轴、y轴分别交于点A(4,0),B(0,2),点C为线段AB上任意一点,过点C作CD⊥OA于点D,延长DC至点E使CE
=
DC,作EF⊥y轴于点F,则四边形ODEF的周长为
_________
.
10.已知函数y
=
(m
+
1)x
+
2
m-
6.
(1)若函数图象过(
-
1,2),求此函数的解析式.
(2)若函数图象与直线y
=
2x
+
5平行,求其函数的解析式.
(3)求满足条件(2)的直线与直线y
=-3x
+
1的交点.
11.小慧根据学习函数的经验,对函数y
=
|x
-
1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y
=
|x
-
1|的自变量x的取值范围是
_________
.
(2)列表,找出y与x的几组对应值:其中,b
=
_________
.
(3)在如图的平面直角坐标系中,描出以上表中各组对应值为坐标的点,并画出该函数的图象.
(4)写出该函数的一条性质:
_________
.
12.如图,在平面直角坐标系中,正比例函数y
=
x与一次函数y
=-x
+
7的图象交于点A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交
y
=
x和y
=-x
+
7的图象于点B,C,连结OC.若BC
=
OA,求△OBC的面积.
13.如果一次函数y
=
kx
+
b的图象经过点(m,1)和点(-1,m),其中m
>
1,那么k,b应满足的条件是( ).
A.k
>
0且b
>
0
B.k
<
0且b
>
1
C.k
>
0且b
<
0
D.k
<
0且b
<
1
14.已知一次函数y
=-
x
+
m和y
=
2x
+
n的图象都经过A(-
4,0),且与y轴分别交于B,C两点,则△ABC的面积为( ).
A.48
B.36
C.24
D.18
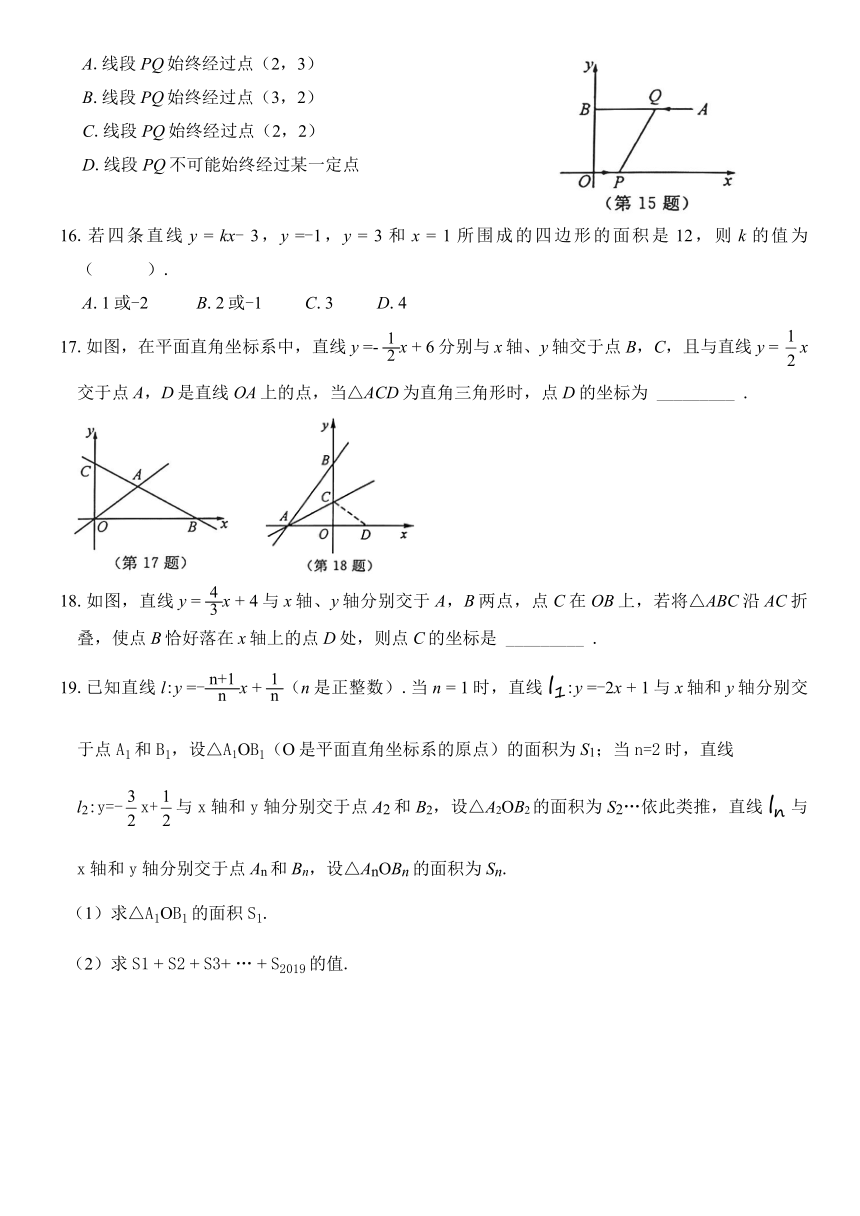
15.如图,在平面直角坐标系中,点A的坐标为(9,6),AB⊥y轴,垂足为点B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P,Q同时停止运动.若点P与点Q的速度之比为1:2,则下列说法正确的是( ).
A.线段PQ始终经过点(2,3)
B.线段PQ始终经过点(3,2)
C.线段PQ始终经过点(2,2)
D.线段PQ不可能始终经过某一定点
16.若四条直线y
=
kx-
3,y
=-1,y
=
3和x
=
1所围成的四边形的面积是12,则k的值为( ).
A.1或-2
B.2或-1
C.3
D.4
17.如图,在平面直角坐标系中,直线y
=-
x
+
6分别与x轴、y轴交于点B,C,且与直线y
=
x交于点A,D是直线OA上的点,当△ACD为直角三角形时,点D的坐标为
_________
.
18.如图,直线y
=
x
+
4与x轴、y轴分别交于A,B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则点C的坐标是
_________
.
19.已知直线l:y
=-x
+
(n是正整数).当n
=
1时,直线l1:y
=-2x
+
1与x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
l2:y=-x+与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2…依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
(1)求△A1OB1的面积S1.
(2)求S1
+
S2
+
S3+
…
+
S2019的值.
20.如图,在平面直角坐标系中,直线AB:y
=-x
+
b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标.
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积.
②当S△ABP
=
8时,求点P的坐标.
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
拓展提优
1.已知将直线y
=
x-1向上平移2个单位长度后得到直线y
=
kx
+
b,则下列关于直线y
=
kx
+
b的说法正确的是( ).
A.经过第一、二、四象限
B.与x轴交于点(1,0)
C.与y轴交于点(0,1)
D.y随x的增大而减小
2.已知一系列直线y
=
akx
+
b(ak均不相等且不为零,ak同号,k为大于或等于2的整数,b
>
0)分别与直线y
=
0相交于一系列点Ak,设Ak的横坐标为x
k,则对于式(1≤i≤k,1≤j≤k,i≠j),下列一定正确的是( ).
A.大于1
B.大于0
C.小于-1
D.小于0
3.如图,在平面直角坐标系中,点A,B的坐标分别为(1,3),(n,3),若直线y
=
2x与线段
AB有公共点,则n的值可以为
_________
.(写出一个即可)
4.如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y
=
x
+
b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A
2018的纵坐标是
_________
.
5.在平面直角坐标系中,一次函数y
=
kx
+
b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当
-
2
<
x≤3时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m-
n
=
4,求点P的坐标.
6.如图,在平面直角坐标系中,一次函数y
=-x
+
5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的函数表达式.
(2)求S△AOC-
S△BOC的值.
(3)一次函数y
=
kx
+
1的图象为l3,且l1,l2,l3不能围成三角形,直接写出k的值.
冲刺重高
1.将函数y
=
2x
+
b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y
=
|2x
+
b|(b为常数)的图象.若该图象在直线y
=
2下方的点的横坐标x满足0
<
x
<
3,则b的取值范围是( ).
A.
-4≤b≤-
2
B.
-
6≤b≤2
C.-4≤b≤2
D.-8≤b≤-2
2.已知直线AB的方程为y
=
kx
+
m,且经过点A(a,a),B(b,8b)(a
>
0,b
>
0),当为整数时,满足条件的整数k有( ).
A.1个
B.2个
C.3个
D.4个
3.2002年在北京召开的世界数学大会的会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1,B2,B3,…,Bn,和C1,C2,C3,…,Cn,分别在直线y
=-x
+
+
1和x轴上,则第n个阴影正方形的面积为
_________
.
第3题
第4题
4.如图,多边形OABCDE在平面直角坐标系中,O为坐标原点,点A和点E分别在y轴和x轴上,其中AB∥CD∥x轴,DE∥BC∥y轴,已知点B(4,6),点D(6,4),若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式为
_________
.
5.在平面直角坐标系中,O为原点,直线l:x
=
1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(1)若点M的坐标为(1,-
1).
①当点F的坐标为(1,1)时,如图,求点P的坐标.
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(2)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,连结OQ,当OQ
=
PQ时,试用含t的式子表示m.
姓名
班级
学号
基础巩固
1.若点(m,n)在函数y
=
2x
+
1的图象上,则2
m
-
n的值是( ).
A.2
B.-
2
C.1
D.-1
2.在一次函数y
=
ax
-
a中,y随x的增大而减小,则其图象可能是( ).
3.若点M(-
7,m),N(-
8,n)都在函数y
=-(k2
+
2k
+
4)x
+
1(k为常数)的图象上,则m和n的大小关系是( ).
A.m
>
n
B.m
<
n
C.m
=
n
D.不能确定
4.如图,已知直线l:y
=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点
A2…按此作法继续下去,则点A4的坐标为( ).
A.(0,64)
B.(0,128)
C.(0,256)
D.(0,512)
5.如图,已知A(5,0),直线y
=
x
+
b(b
>
0)与y轴交于点B,连结AB,∠=
75°,则b的值为( ).
A.3
B.
C.4
D.
6.直线y
=
2x
+
6与两坐标轴围成的三角形面积是
_________
.
7.如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y
=-x上,则点B与其对应点B′间的距离为
_________
.
8.如图,在平面直角坐标系中,函数y
=
x和y
=-x的图象分别为直线l1,
l2,过点A1
(1,-)作x轴的垂线交l1于点A2,过点A2作y轴的垂线交l2于点A3,过点A3作x轴的垂线交l1于点A4,过点A4作y轴的垂线交l于点A5……依次进行下去,则点A2018的横坐标为
_________
.
第8题
第9题
9.如图,在平面直角坐标系中,直线y
=
kx
+
b与x轴、y轴分别交于点A(4,0),B(0,2),点C为线段AB上任意一点,过点C作CD⊥OA于点D,延长DC至点E使CE
=
DC,作EF⊥y轴于点F,则四边形ODEF的周长为
_________
.
10.已知函数y
=
(m
+
1)x
+
2
m-
6.
(1)若函数图象过(
-
1,2),求此函数的解析式.
(2)若函数图象与直线y
=
2x
+
5平行,求其函数的解析式.
(3)求满足条件(2)的直线与直线y
=-3x
+
1的交点.
11.小慧根据学习函数的经验,对函数y
=
|x
-
1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y
=
|x
-
1|的自变量x的取值范围是
_________
.
(2)列表,找出y与x的几组对应值:其中,b
=
_________
.
(3)在如图的平面直角坐标系中,描出以上表中各组对应值为坐标的点,并画出该函数的图象.
(4)写出该函数的一条性质:
_________
.
12.如图,在平面直角坐标系中,正比例函数y
=
x与一次函数y
=-x
+
7的图象交于点A.
(1)求点A的坐标.
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交
y
=
x和y
=-x
+
7的图象于点B,C,连结OC.若BC
=
OA,求△OBC的面积.
13.如果一次函数y
=
kx
+
b的图象经过点(m,1)和点(-1,m),其中m
>
1,那么k,b应满足的条件是( ).
A.k
>
0且b
>
0
B.k
<
0且b
>
1
C.k
>
0且b
<
0
D.k
<
0且b
<
1
14.已知一次函数y
=-
x
+
m和y
=
2x
+
n的图象都经过A(-
4,0),且与y轴分别交于B,C两点,则△ABC的面积为( ).
A.48
B.36
C.24
D.18
15.如图,在平面直角坐标系中,点A的坐标为(9,6),AB⊥y轴,垂足为点B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P,Q同时停止运动.若点P与点Q的速度之比为1:2,则下列说法正确的是( ).
A.线段PQ始终经过点(2,3)
B.线段PQ始终经过点(3,2)
C.线段PQ始终经过点(2,2)
D.线段PQ不可能始终经过某一定点
16.若四条直线y
=
kx-
3,y
=-1,y
=
3和x
=
1所围成的四边形的面积是12,则k的值为( ).
A.1或-2
B.2或-1
C.3
D.4
17.如图,在平面直角坐标系中,直线y
=-
x
+
6分别与x轴、y轴交于点B,C,且与直线y
=
x交于点A,D是直线OA上的点,当△ACD为直角三角形时,点D的坐标为
_________
.
18.如图,直线y
=
x
+
4与x轴、y轴分别交于A,B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则点C的坐标是
_________
.
19.已知直线l:y
=-x
+
(n是正整数).当n
=
1时,直线l1:y
=-2x
+
1与x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
l2:y=-x+与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2…依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
(1)求△A1OB1的面积S1.
(2)求S1
+
S2
+
S3+
…
+
S2019的值.
20.如图,在平面直角坐标系中,直线AB:y
=-x
+
b交y轴于点A(0,4),交x轴于点B.
(1)求直线AB的表达式和点B的坐标.
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积.
②当S△ABP
=
8时,求点P的坐标.
③在②的条件下,以PB为斜边在第一象限作等腰直角△PBC,求点C的坐标.
拓展提优
1.已知将直线y
=
x-1向上平移2个单位长度后得到直线y
=
kx
+
b,则下列关于直线y
=
kx
+
b的说法正确的是( ).
A.经过第一、二、四象限
B.与x轴交于点(1,0)
C.与y轴交于点(0,1)
D.y随x的增大而减小
2.已知一系列直线y
=
akx
+
b(ak均不相等且不为零,ak同号,k为大于或等于2的整数,b
>
0)分别与直线y
=
0相交于一系列点Ak,设Ak的横坐标为x
k,则对于式(1≤i≤k,1≤j≤k,i≠j),下列一定正确的是( ).
A.大于1
B.大于0
C.小于-1
D.小于0
3.如图,在平面直角坐标系中,点A,B的坐标分别为(1,3),(n,3),若直线y
=
2x与线段
AB有公共点,则n的值可以为
_________
.(写出一个即可)
4.如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y
=
x
+
b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A
2018的纵坐标是
_________
.
5.在平面直角坐标系中,一次函数y
=
kx
+
b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当
-
2
<
x≤3时,求y的取值范围.
(2)已知点P(m,n)在该函数的图象上,且m-
n
=
4,求点P的坐标.
6.如图,在平面直角坐标系中,一次函数y
=-x
+
5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的函数表达式.
(2)求S△AOC-
S△BOC的值.
(3)一次函数y
=
kx
+
1的图象为l3,且l1,l2,l3不能围成三角形,直接写出k的值.
冲刺重高
1.将函数y
=
2x
+
b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y
=
|2x
+
b|(b为常数)的图象.若该图象在直线y
=
2下方的点的横坐标x满足0
<
x
<
3,则b的取值范围是( ).
A.
-4≤b≤-
2
B.
-
6≤b≤2
C.-4≤b≤2
D.-8≤b≤-2
2.已知直线AB的方程为y
=
kx
+
m,且经过点A(a,a),B(b,8b)(a
>
0,b
>
0),当为整数时,满足条件的整数k有( ).
A.1个
B.2个
C.3个
D.4个
3.2002年在北京召开的世界数学大会的会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1,B2,B3,…,Bn,和C1,C2,C3,…,Cn,分别在直线y
=-x
+
+
1和x轴上,则第n个阴影正方形的面积为
_________
.
第3题
第4题
4.如图,多边形OABCDE在平面直角坐标系中,O为坐标原点,点A和点E分别在y轴和x轴上,其中AB∥CD∥x轴,DE∥BC∥y轴,已知点B(4,6),点D(6,4),若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式为
_________
.
5.在平面直角坐标系中,O为原点,直线l:x
=
1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称,直线EA与直线OF交于点P.
(1)若点M的坐标为(1,-
1).
①当点F的坐标为(1,1)时,如图,求点P的坐标.
②当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
(2)若点M(1,m),点F(1,t),其中t≠0,过点P作PQ⊥l于点Q,连结OQ,当OQ
=
PQ时,试用含t的式子表示m.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
