3.4圆周角(1)

(共21张PPT)
O
A
B
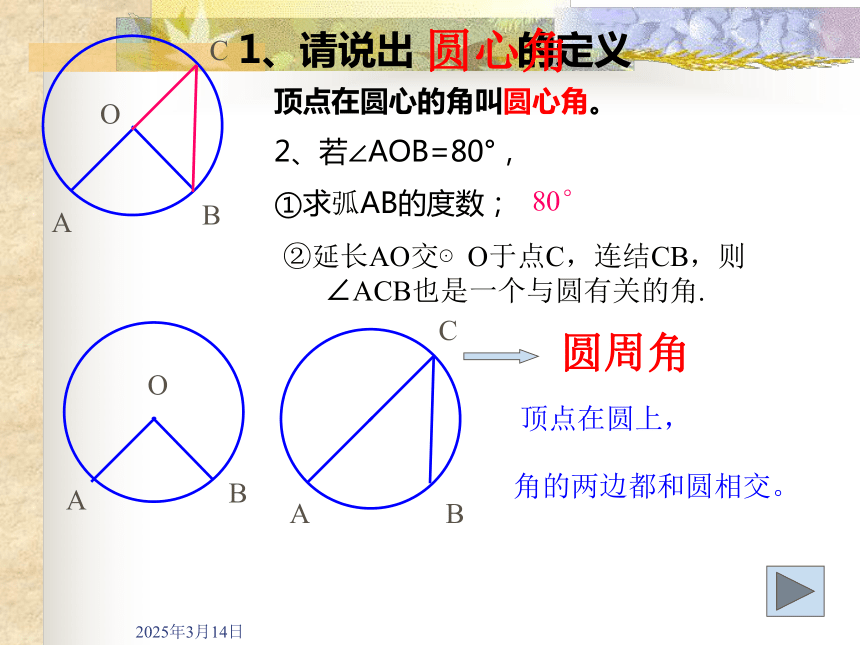
角的两边都和圆相交。
1、请说出 的定义
顶点在圆心的角叫圆心角。
2、若∠AOB=80°，
①求弧AB的度数；
C
80°
②延长AO交⊙O于点C，连结CB，则∠ACB也是一个与圆有关的角.
O
A
B
B
A
C
圆周角
顶点在圆上，
圆心角
找一找你认识的新朋友：圆周角。
找一找:找出图中的圆周角.
A
B
C
D
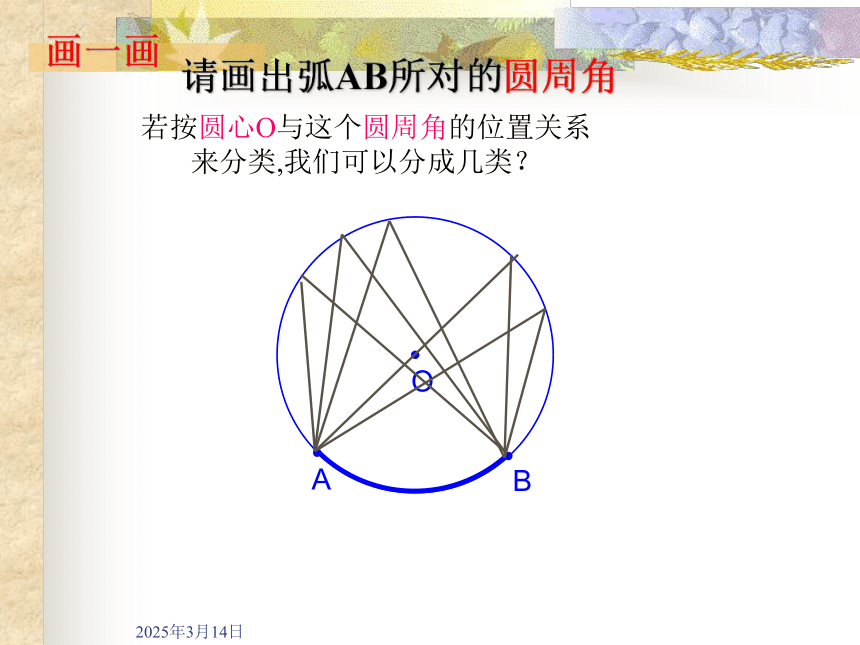
画一画
请画出弧AB所对的圆周角
若按圆心O与这个圆周角的位置关系
来分类,我们可以分成几类？
A
B
O
C
A
B
O
C
A
B
O
C
⑶
⑴
⑵
D
D
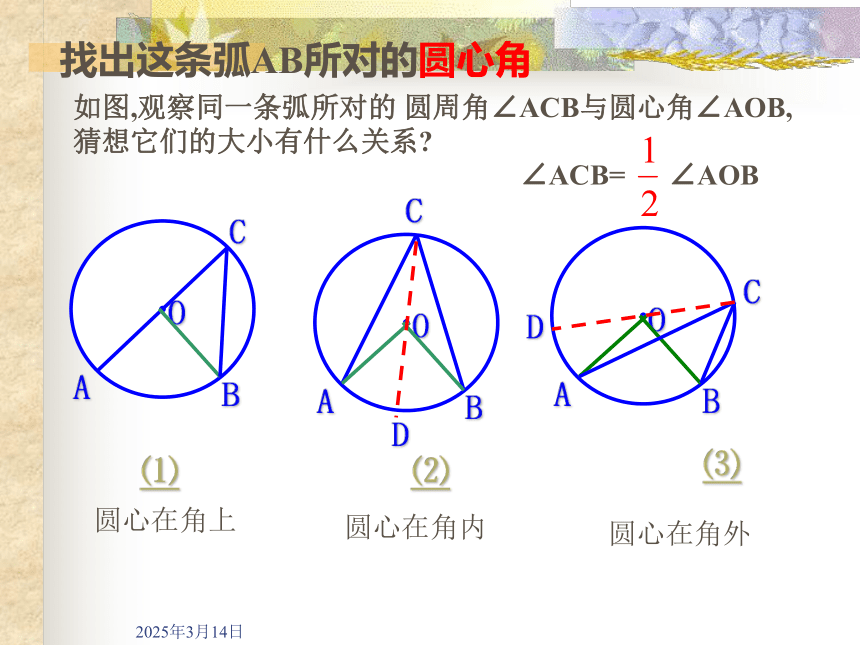
找出这条弧AB所对的圆心角
圆心在角上
圆心在角内
圆心在角外
如图,观察同一条弧所对的 圆周角∠ACB与圆心角∠AOB,
猜想它们的大小有什么关系
∠ACB= ∠AOB
圆周角定理：
一条弧所对圆周角等于它所对圆心角的一半。
推论1、圆周角的度数等于它所对弧度数的一半。
圆心角的度数等于它所对弧的度数。
A
B
C
O
1.若∠AOB=50°,则∠C=_________.
解: ∠C = ∠AOB = 25°.
A
B
O
C
如图,AB是直径,则∠ACB=＿＿＿＿
90 度
半圆（或直径）所对的圆周角是直角，
90度的圆周角所对的弦是直径。
推论2：
A
B
O
C
A
B
C
O
1
2
例1：已知:如图,四边形ABCD的四个顶点在⊙O上，求证：∠B+∠D=1800
例题欣赏
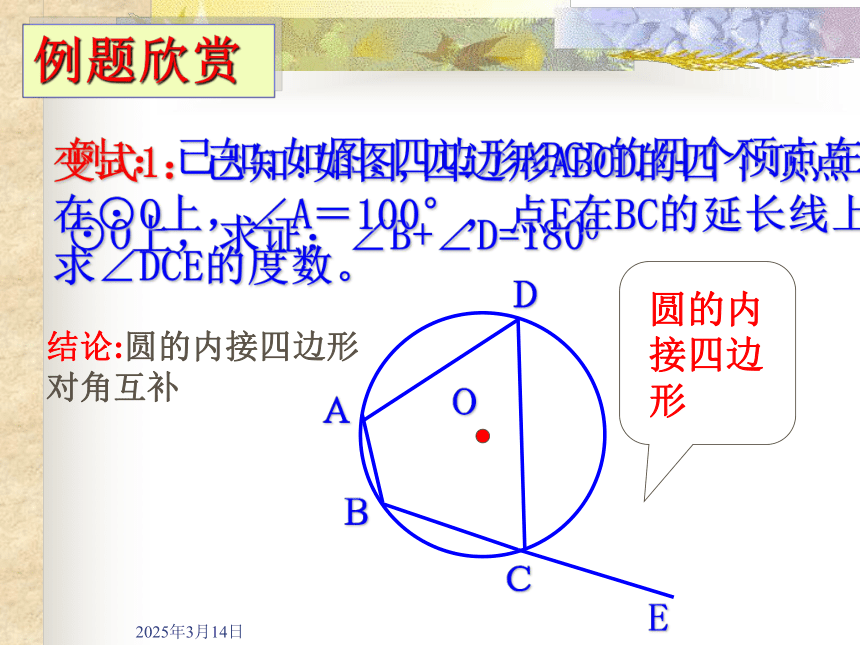
变式1：已知:如图,四边形ABCD的四个顶点在⊙O上，∠A＝100°，点E在BC的延长线上，求∠DCE的度数。
Ｏ
Ｃ
Ｂ
Ａ
Ｄ
E
圆的内接四边形
结论:圆的内接四边形对角互补
Ｏ
Ｃ
Ｂ
Ａ
Ｄ
例题欣赏
变式2：如图, B是AC上的一点，∠AOC＝n°，求∠ABC的度数 。
⌒
变式3：如图,在⊙O中，∠AOC=1200，∠ACB=250,求∠BAC的度数。
易错题:已知⊙O中弦AB的等于半径，
求弦AB所对的圆心角和圆周角的度数。
O
A
B
圆心角为60度
圆周角为 30 度
或 150 度。
C
D
小结:
本节课你学到了什么
1、圆周角的概念
2、圆周角的定理。一条弧所对的圆周角等于它所对的圆心角的一半。
3、圆周角定理的两个推论：圆周角的度数等于它所对弧度数的一半；半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。
4、圆内接四边形对角互补。
A
B
O
C
若OA//BC, ∠C= 25°, 则∠ADB=_______
D
变式：
A
B
C
P
O
若∠C= 25°,点P在弧AB间滑动,
则∠AOP的取值范围是______
变式：
如图，以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_____ ;
(2)OC与BD的位置关系是_____ ;
(3)若OC = 2cm,则BD = __ cm。
OC垂直平分AD
平 行
4
C
D
O1
A
B
O
过点C作直径CD.由1可得:
圆周角和圆心角的关系
A
B
C
能否转化为第1种情况
A
B
C
O
D
O
∠ACD = ∠AOD,∠BCD = ∠BOD
即∠ACB = ∠AOB.
∴ ∠ACD +∠BCD = (∠AOD+∠BOD)
1
圆周角和圆心角的关系
1.首先考虑一种特殊情况：
∵∠AOB是△BCO的外角，
∴∠AOB=∠B+∠C.
∵OC=OB，
∴∠B=∠C.
∴∠AOB=2∠C
即∠C = ∠AOB.
A
B
C
O
1
圆周角和圆心角的关系
A
B
O
C
能否也转化为第1种情况
A
B
C
O
D
过点C作直径BD.由1可得:
∠ACD = ∠AOD,∠BCD = ∠BOD,
∴ ∠BCD - ∠ACD = (∠BOD- ∠AOD)
即∠ACB= ∠AOB
1
B
A
C
B
A
C