浙教版初中数学八年级上 册2.7 探索勾股定理课件(1)(25张)
文档属性
| 名称 | 浙教版初中数学八年级上 册2.7 探索勾股定理课件(1)(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 771.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 19:22:53 | ||
图片预览





文档简介
(共25张PPT)
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
2.有两个角互余的三角形是直角三角形
3、如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.
复习回顾
2.7
探索勾股定理(1)
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
结论:
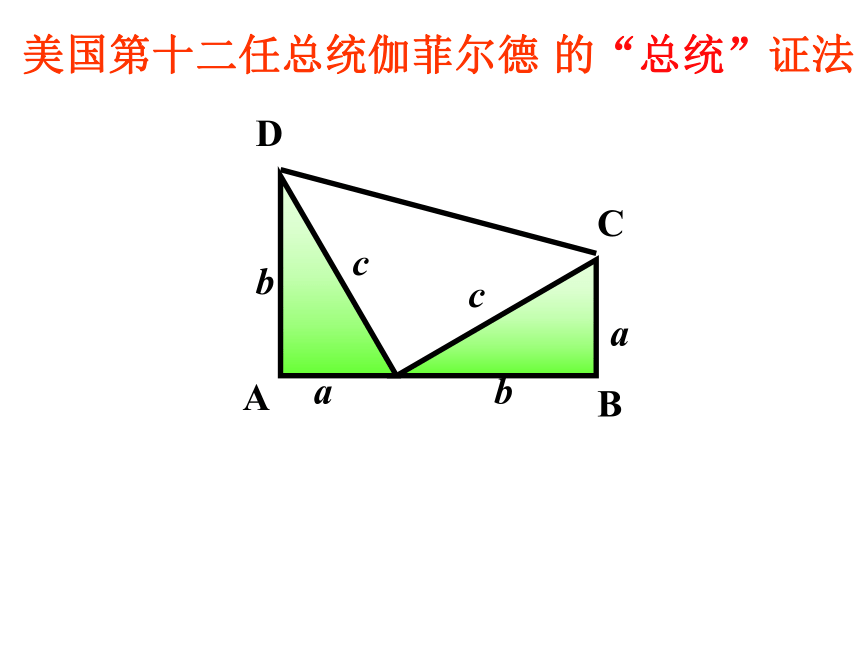
美国第十二任总统伽菲尔德
的“总统”证法
b
c
a
b
c
a
A
B
C
D
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。
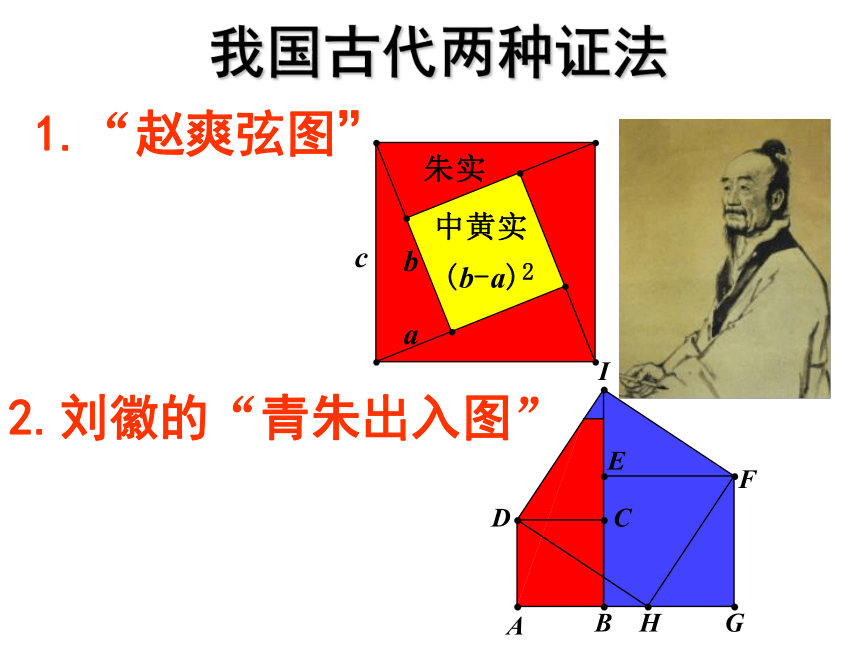
我国古代两种证法
1.“赵爽弦图”
2.刘徽的“青朱出入图”
c
c
c
b
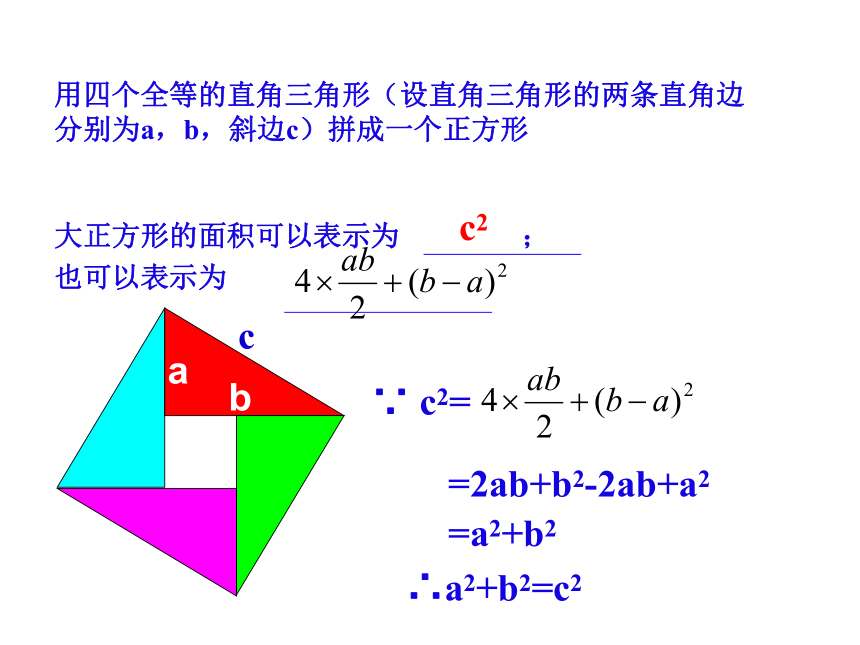
∵
c2=
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
c2
a
b
用四个全等的直角三角形(设直角三角形的两条直角边
分别为a,b,斜边c)拼成一个正方形
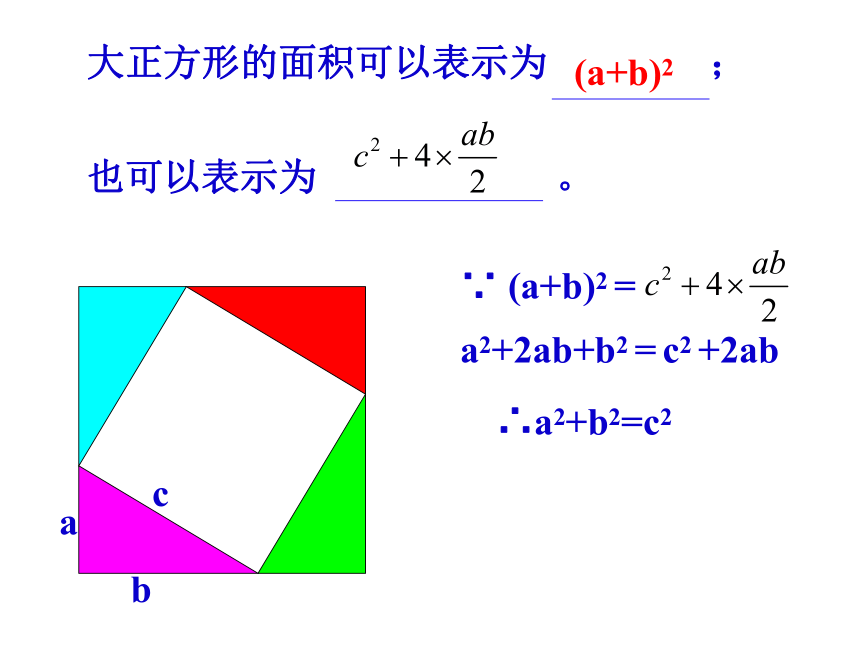
∵
(a+b)2
=
a2+2ab+b2
=
c2
+2ab
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
。
(a+b)2
c
a
b
c
a
b
c
a
b
c
a
b
例1、已知△ABC中,
∠C=Rt∠,BC=a,AC=b,AB=C
已知:
a=2,
b=3,
求c;
已知:
a=15,
c=17,
求b;
(3)已知:c=15,a:b=3:4,求a,b.
(1)直角三角形的两直角边为3和4,则斜边为___
(3)直角三角形的两直角边为6和8,则斜边上的中线为___;斜边上的高线为___
(2)直角三角形的两直角边为5和12,则斜边为___
比一比谁最快
两边长
5
5
13
4.8
(4)已知△ABC中,
∠B=Rt∠,BC=a,AC=b,AB=C
a=1,
b=3,
求c;
x
例2、如图,你能计算出下列直角三角形中未知边的长吗?
2
反思:若要你在数轴上准确表示
,你会参考上面的结果画吗?
小结:利用勾股定理可以解决直角三角形的边长。
-1
0
1
2
1
x
0
2
解:由勾股定理得x?=1?+2?=5
∵x>0
∴x=
试一试:你能在数轴上准确表示
吗?
如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
y=0
生活应用一
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
想知道学校旗杆的高度吗?
探索
5米
1米
y=0
生活应用二
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
x
2
x+0.5
0.5
C
A
B
挑战数学家
解:
∴AC=
(1)∵∠ACB=90°AB=4,BC=1.4
=
(2)
A
A′
B
B′
5m
0.7m
C
∴
AB2=AC2+BC2
一架长5米的梯子AB,斜靠在一竖直墙AC上,这时梯足B到墙底端C的距离为1.4米.
(1)此时梯子顶端A距离地面多高?
(2)若梯子的顶端沿墙下滑0.8米,那么梯足B是否也外移了0.8米?
探究
y=0
生活应用三
小结
你学会了什么?
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
1.求下列图中数与字母所代表的正方形面积:
10
15
A
6
25
B
=25
=19
抢答
A
B
C
D
7cm
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
毕达哥拉斯树
毕达哥拉斯树
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,
若斜边AB=3,则图中阴影部分的面积为______
?
?
在直线l上依次摆放着五个正方形,如图所示,
已知倾斜放置的两个正方形的面积分别是3,5,
正放置的三个正方形的面积依次是S1,S2,S3,则S1+2S2+S3=
._________
如图,以直角三角形三边为直径的三个半圆面积A、B、C之间有怎样的关系:
思考题
D
思考题
如图,以直角三角形三边为边作三个等边三角形,其面积分别为A、B、C之间有怎样的关系:
A
B
C
如图,牧童在A处放牛,牧童家在B处,A,B处相距河岸
的距离AC,BD分别为500
m和300
m,且C,D两处的距离为
600
m,天黑前牧童从A处将牛牵到河边去饮水,再赶回家,
那么牧童最少要走多少米?
直角三角形的判定
1.有一个角是直角的三角形叫做直角三角形
2.有两个角互余的三角形是直角三角形
3、如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形.
复习回顾
2.7
探索勾股定理(1)
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
结论:
美国第十二任总统伽菲尔德
的“总统”证法
b
c
a
b
c
a
A
B
C
D
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。
我国古代两种证法
1.“赵爽弦图”
2.刘徽的“青朱出入图”
c
c
c
b
∵
c2=
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
c2
a
b
用四个全等的直角三角形(设直角三角形的两条直角边
分别为a,b,斜边c)拼成一个正方形
∵
(a+b)2
=
a2+2ab+b2
=
c2
+2ab
∴a2+b2=c2
大正方形的面积可以表示为
;
也可以表示为
。
(a+b)2
c
a
b
c
a
b
c
a
b
c
a
b
例1、已知△ABC中,
∠C=Rt∠,BC=a,AC=b,AB=C
已知:
a=2,
b=3,
求c;
已知:
a=15,
c=17,
求b;
(3)已知:c=15,a:b=3:4,求a,b.
(1)直角三角形的两直角边为3和4,则斜边为___
(3)直角三角形的两直角边为6和8,则斜边上的中线为___;斜边上的高线为___
(2)直角三角形的两直角边为5和12,则斜边为___
比一比谁最快
两边长
5
5
13
4.8
(4)已知△ABC中,
∠B=Rt∠,BC=a,AC=b,AB=C
a=1,
b=3,
求c;
x
例2、如图,你能计算出下列直角三角形中未知边的长吗?
2
反思:若要你在数轴上准确表示
,你会参考上面的结果画吗?
小结:利用勾股定理可以解决直角三角形的边长。
-1
0
1
2
1
x
0
2
解:由勾股定理得x?=1?+2?=5
∵x>0
∴x=
试一试:你能在数轴上准确表示
吗?
如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
y=0
生活应用一
温馨提示:在实际问题中,要会根据需要构造直角三角形,再通过勾股定理来解决问题.
想知道学校旗杆的高度吗?
探索
5米
1米
y=0
生活应用二
印度数学家什迦逻(1141年-1225年?)
曾提出过“荷花问题”:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
x
2
x+0.5
0.5
C
A
B
挑战数学家
解:
∴AC=
(1)∵∠ACB=90°AB=4,BC=1.4
=
(2)
A
A′
B
B′
5m
0.7m
C
∴
AB2=AC2+BC2
一架长5米的梯子AB,斜靠在一竖直墙AC上,这时梯足B到墙底端C的距离为1.4米.
(1)此时梯子顶端A距离地面多高?
(2)若梯子的顶端沿墙下滑0.8米,那么梯足B是否也外移了0.8米?
探究
y=0
生活应用三
小结
你学会了什么?
勾股定理
(a2+b2=c2)
直角三角形
中的应用
已知任意两条边,
就可以求第三边.
已知一条边,以及另
两条边之间的关系,
就可以求另两条边的
长度.
1.求下列图中数与字母所代表的正方形面积:
10
15
A
6
25
B
=25
=19
抢答
A
B
C
D
7cm
2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。
49
毕达哥拉斯树
毕达哥拉斯树
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形,
若斜边AB=3,则图中阴影部分的面积为______
?
?
在直线l上依次摆放着五个正方形,如图所示,
已知倾斜放置的两个正方形的面积分别是3,5,
正放置的三个正方形的面积依次是S1,S2,S3,则S1+2S2+S3=
._________
如图,以直角三角形三边为直径的三个半圆面积A、B、C之间有怎样的关系:
思考题
D
思考题
如图,以直角三角形三边为边作三个等边三角形,其面积分别为A、B、C之间有怎样的关系:
A
B
C
如图,牧童在A处放牛,牧童家在B处,A,B处相距河岸
的距离AC,BD分别为500
m和300
m,且C,D两处的距离为
600
m,天黑前牧童从A处将牛牵到河边去饮水,再赶回家,
那么牧童最少要走多少米?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
