2020年秋浙教版数学八年级上册第四章《图形与坐标》综合提高B卷(Word版 含答案)
文档属性
| 名称 | 2020年秋浙教版数学八年级上册第四章《图形与坐标》综合提高B卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-14 23:02:04 | ||
图片预览



文档简介
2020年秋浙教版数学八年级上册第四章《图形与坐标》综合提高B卷
姓名
班级
学号
一、选择题(每题3分,共30分)
1.如图所示,被手盖住的点的坐标可能为
(
)
A.(-
4,-
6)
B.(-
6,3)
C.(5,2)
D.(3,-
4)
2.若线段AB∥x轴且AB
=
3,点A的坐标为(2,1),则点B的坐标为(
)
A.(5,1)
B.(-
1,1)
C.(5,1)或(-
1.1)
D.(2,4)或(2,-
2)
3.已知点P(3a-3,1-2a)关于x轴的对称点位于第三象限,则a的取值范围在数轴上表示正确的是( )
4.在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a,则所得的图案与原来图案相比(
)
A.形状不变,大小扩大到原来的a倍
B.图案向右平移了a个单位
C.图案向上平移了a个单位
D.图案向右平移了a个单位,并且向上平移了a个单位
5.在平面直角坐标系中,已知点A(-2a,6)与点B(4,b
+
2)关于x轴对称,则a,b的值为(
)
A.a
=
2,b
=-8
B.a
=
2,b
=
8
C.a
=-2,b
=
8
D.a
=-2,b
=-8
6.已知点P(,)在y轴上,则点P的坐标为(
)
A.(0,-)
B.(,0)
C.(0,)
D.(-1,0)
7.如图所示,线段AB经过平移得到线段AB,其中A,B的对应点分别为A1,B1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在AB上的对应点P的坐标为(
)
A.(a
-
4,b
+
2)
B.(a
-
4,b
-
2)
C.(a
+
4,b
+
2)
D.(a
+
4,b
-
2)
8.已知点P坐标为(2
-
a,3a
+
6),且点P到两坐标轴的距离相等,则a的值是(
)
A.-1或4
B.1或4
C.1或-4
D.-1或-4
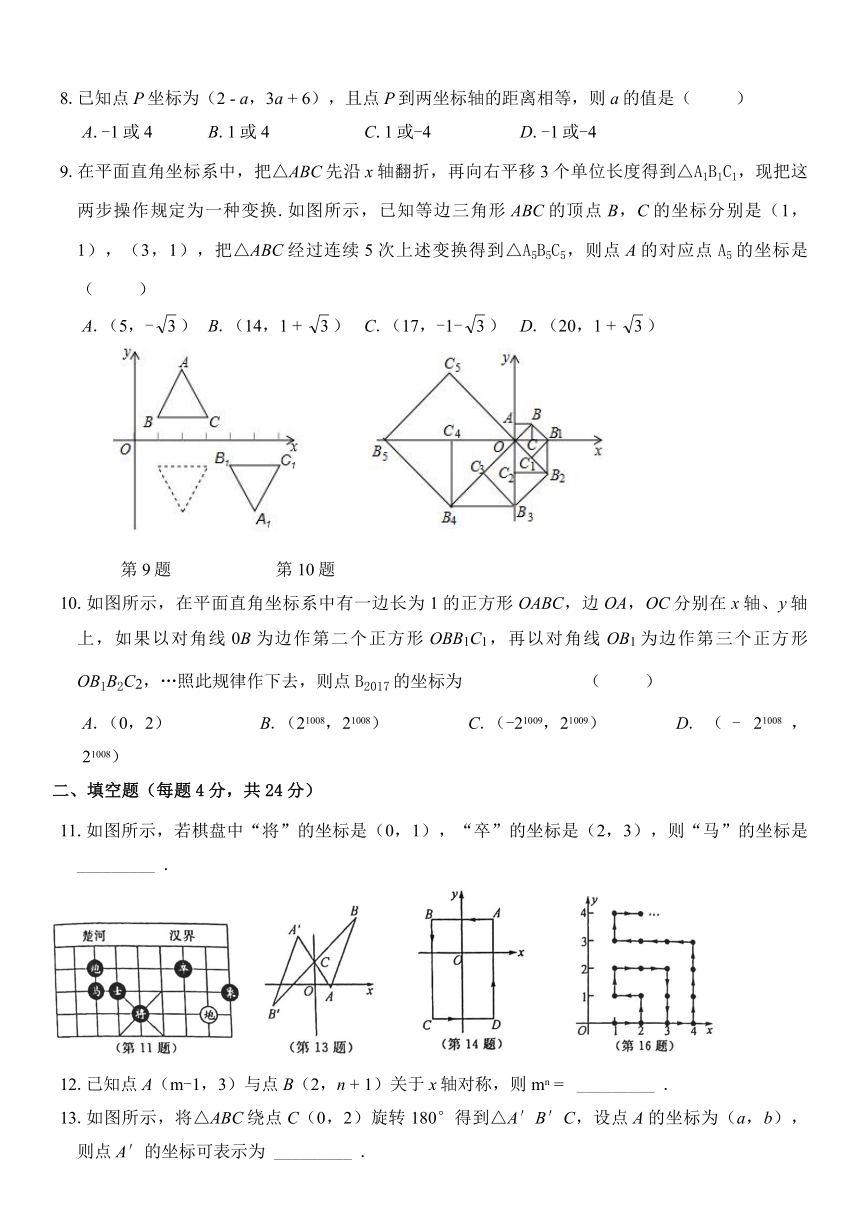
9.在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位长度得到△A1B1C1,现把这两步操作规定为一种变换.如图所示,已知等边三角形ABC的顶点B,C的坐标分别是(1,1),(3,1),把△ABC经过连续5次上述变换得到△A5B5C5,则点A的对应点A5的坐标是(
)
A.(5,-)
B.(14,1
+
)
C.(17,-1-)
D.(20,1
+
)
第9题
第10题
10.如图所示,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线0B为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…照此规律作下去,则点B2017的坐标为
(
)
A.(0,2)
B.(21008,21008)
C.(-21009,21009)
D.(-
21008,21008)
二、填空题(每题4分,共24分)
11.如图所示,若棋盘中“将”的坐标是(0,1),“卒”的坐标是(2,3),则“马”的坐标是
_________
.
12.已知点A(m-1,3)与点B(2,n
+
1)关于x轴对称,则mn
=
_________
.
13.如图所示,将△ABC绕点C(0,2)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标可表示为
_________
.
14.如图所示,在平面直角坐标系中,已知点A(1,1),B(-
1,1),C(-1,-2),D(1,-2).现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-
D-A-
…的顺序紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
_________
.
15.在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax
+
y,x
+
ay),其中a为常数,则称点Q是点P的“a
级关联点”,例如:点P(1,4)的“3级关联点”为Q(3
×
1
+
4,1
+
3
×
4),即Q(7,13).若点B的“2级关联点“是B′(3,3),则点B的坐标为
_________
;已知点M(m
-1,2
m)的”-
3级关联点“M′位于y轴上,则M′的坐标为
_________
.
16.如图所示,在平面直角坐标系中,有若干个横纵坐标均为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…,则第81个点的横坐标为
_________
三、解答题(共66分)
17.(6分)如图所示为小明家O和学校A所在地的简单地图,已知OA
=
2
cm,OB
=
2.5
cm,OP
=
4
cm,C为OP的中点.
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
(3)若学校距离小明家400
m,则商场和停车场分别距离小明家多少米?
8.(8分)已知平面直角坐标系中有一点M(m-1,2
m
+
3).
(1)当点M到x轴的距离为1时,求点M的坐标.
(2)当点N的坐标为(5,-1)且MN∥x轴时,求点M的坐标.
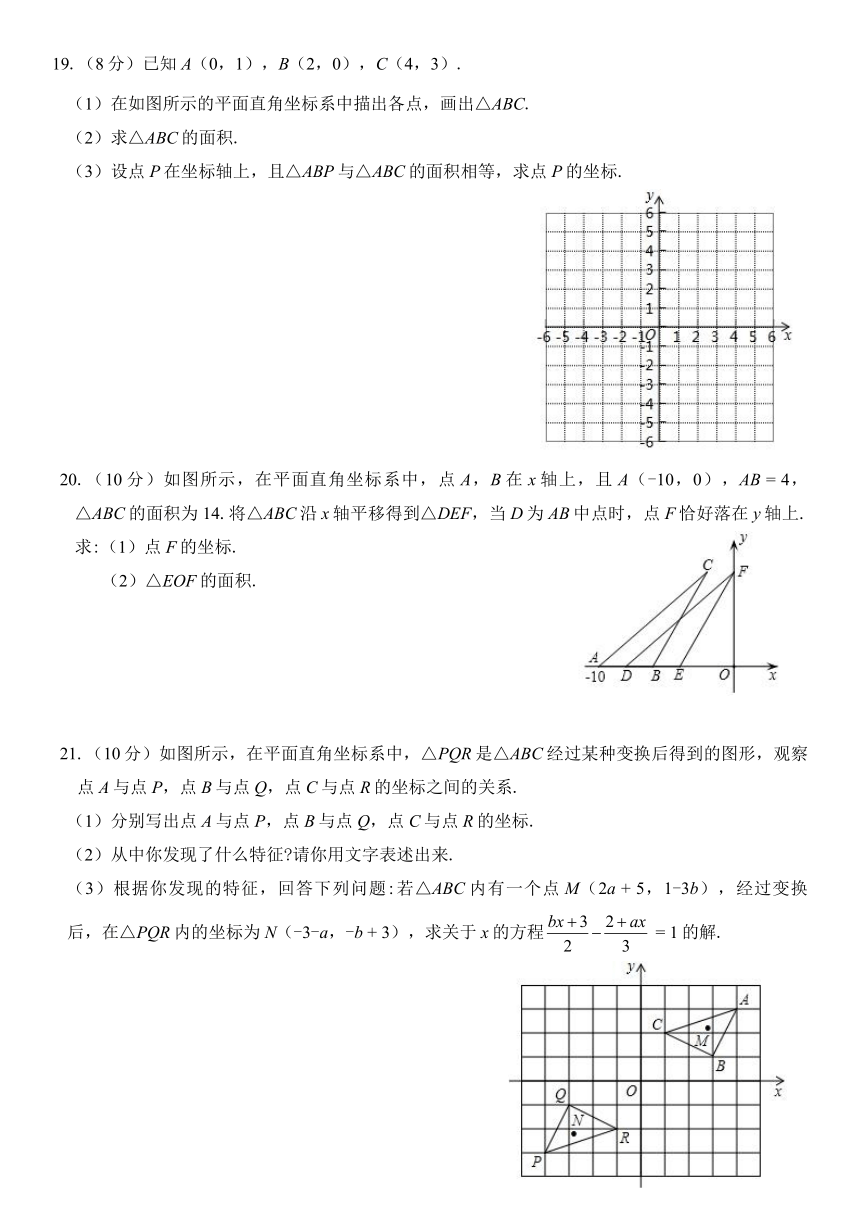
19.(8分)已知A(0,1),B(2,0),C(4,3).
(1)在如图所示的平面直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积.
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
20.(10分)如图所示,在平面直角坐标系中,点A,B在x轴上,且A(-10,0),AB
=
4,△ABC的面积为14.将△ABC沿x轴平移得到△DEF,当D为AB中点时,点F恰好落在y轴上.求:(1)点F的坐标.
(2)△EOF的面积.
21.(10分)如图所示,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.
(1)分别写出点A与点P,点B与点Q,点C与点R的坐标.
(2)从中你发现了什么特征?请你用文字表述出来.
(3)根据你发现的特征,回答下列问题:若△ABC内有一个点M(2a
+
5,1-3b),经过变换后,在△PQR内的坐标为N(-3-a,-b
+
3),求关于x的方程
=
1的解.
22.(12分)在平面直角坐标系中、O为坐标原点,点A(a,a)位于第一象限,点B(0,3),点C(c,0),其中0
<
c
<
3,∠BAC
=
90°.
(1)根据题意,画出示意图.
(2)若a
=
2,求OC的长.
(3)已知点D在线段OC上,若OB
2
-
OC
2
=
8S△CAD,四边形OBAD的面积为,求a2
-
a的值.
23.(12分)在平面直角坐标系中,△ABC满足:∠ACB
=
90°,AC
=
2,BC
=
1,点A,C分别在x轴、y轴上,当点A从原点开始在x轴正半轴上运动时,点C随之在y轴正半轴上运动.
(1)当点A在原点时,求原点O到点B的距离OB.
(2)当OA
=
OC时,求原点O到点B的距离OB.
(3)求原点O到点B的距离OB的最大值,并确定此时图形应满足什么条件.
姓名
班级
学号
一、选择题(每题3分,共30分)
1.如图所示,被手盖住的点的坐标可能为
(
)
A.(-
4,-
6)
B.(-
6,3)
C.(5,2)
D.(3,-
4)
2.若线段AB∥x轴且AB
=
3,点A的坐标为(2,1),则点B的坐标为(
)
A.(5,1)
B.(-
1,1)
C.(5,1)或(-
1.1)
D.(2,4)或(2,-
2)
3.已知点P(3a-3,1-2a)关于x轴的对称点位于第三象限,则a的取值范围在数轴上表示正确的是( )
4.在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a,则所得的图案与原来图案相比(
)
A.形状不变,大小扩大到原来的a倍
B.图案向右平移了a个单位
C.图案向上平移了a个单位
D.图案向右平移了a个单位,并且向上平移了a个单位
5.在平面直角坐标系中,已知点A(-2a,6)与点B(4,b
+
2)关于x轴对称,则a,b的值为(
)
A.a
=
2,b
=-8
B.a
=
2,b
=
8
C.a
=-2,b
=
8
D.a
=-2,b
=-8
6.已知点P(,)在y轴上,则点P的坐标为(
)
A.(0,-)
B.(,0)
C.(0,)
D.(-1,0)
7.如图所示,线段AB经过平移得到线段AB,其中A,B的对应点分别为A1,B1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在AB上的对应点P的坐标为(
)
A.(a
-
4,b
+
2)
B.(a
-
4,b
-
2)
C.(a
+
4,b
+
2)
D.(a
+
4,b
-
2)
8.已知点P坐标为(2
-
a,3a
+
6),且点P到两坐标轴的距离相等,则a的值是(
)
A.-1或4
B.1或4
C.1或-4
D.-1或-4
9.在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位长度得到△A1B1C1,现把这两步操作规定为一种变换.如图所示,已知等边三角形ABC的顶点B,C的坐标分别是(1,1),(3,1),把△ABC经过连续5次上述变换得到△A5B5C5,则点A的对应点A5的坐标是(
)
A.(5,-)
B.(14,1
+
)
C.(17,-1-)
D.(20,1
+
)
第9题
第10题
10.如图所示,在平面直角坐标系中有一边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线0B为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…照此规律作下去,则点B2017的坐标为
(
)
A.(0,2)
B.(21008,21008)
C.(-21009,21009)
D.(-
21008,21008)
二、填空题(每题4分,共24分)
11.如图所示,若棋盘中“将”的坐标是(0,1),“卒”的坐标是(2,3),则“马”的坐标是
_________
.
12.已知点A(m-1,3)与点B(2,n
+
1)关于x轴对称,则mn
=
_________
.
13.如图所示,将△ABC绕点C(0,2)旋转180°得到△A′B′C,设点A的坐标为(a,b),则点A′的坐标可表示为
_________
.
14.如图所示,在平面直角坐标系中,已知点A(1,1),B(-
1,1),C(-1,-2),D(1,-2).现把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-
D-A-
…的顺序紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
_________
.
15.在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax
+
y,x
+
ay),其中a为常数,则称点Q是点P的“a
级关联点”,例如:点P(1,4)的“3级关联点”为Q(3
×
1
+
4,1
+
3
×
4),即Q(7,13).若点B的“2级关联点“是B′(3,3),则点B的坐标为
_________
;已知点M(m
-1,2
m)的”-
3级关联点“M′位于y轴上,则M′的坐标为
_________
.
16.如图所示,在平面直角坐标系中,有若干个横纵坐标均为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…,则第81个点的横坐标为
_________
三、解答题(共66分)
17.(6分)如图所示为小明家O和学校A所在地的简单地图,已知OA
=
2
cm,OB
=
2.5
cm,OP
=
4
cm,C为OP的中点.
(1)图中距小明家距离相同的是哪些地方?
(2)商场B、学校A、公园C、停车场P分别在小明家的什么方向?
(3)若学校距离小明家400
m,则商场和停车场分别距离小明家多少米?
8.(8分)已知平面直角坐标系中有一点M(m-1,2
m
+
3).
(1)当点M到x轴的距离为1时,求点M的坐标.
(2)当点N的坐标为(5,-1)且MN∥x轴时,求点M的坐标.
19.(8分)已知A(0,1),B(2,0),C(4,3).
(1)在如图所示的平面直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积.
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
20.(10分)如图所示,在平面直角坐标系中,点A,B在x轴上,且A(-10,0),AB
=
4,△ABC的面积为14.将△ABC沿x轴平移得到△DEF,当D为AB中点时,点F恰好落在y轴上.求:(1)点F的坐标.
(2)△EOF的面积.
21.(10分)如图所示,在平面直角坐标系中,△PQR是△ABC经过某种变换后得到的图形,观察点A与点P,点B与点Q,点C与点R的坐标之间的关系.
(1)分别写出点A与点P,点B与点Q,点C与点R的坐标.
(2)从中你发现了什么特征?请你用文字表述出来.
(3)根据你发现的特征,回答下列问题:若△ABC内有一个点M(2a
+
5,1-3b),经过变换后,在△PQR内的坐标为N(-3-a,-b
+
3),求关于x的方程
=
1的解.
22.(12分)在平面直角坐标系中、O为坐标原点,点A(a,a)位于第一象限,点B(0,3),点C(c,0),其中0
<
c
<
3,∠BAC
=
90°.
(1)根据题意,画出示意图.
(2)若a
=
2,求OC的长.
(3)已知点D在线段OC上,若OB
2
-
OC
2
=
8S△CAD,四边形OBAD的面积为,求a2
-
a的值.
23.(12分)在平面直角坐标系中,△ABC满足:∠ACB
=
90°,AC
=
2,BC
=
1,点A,C分别在x轴、y轴上,当点A从原点开始在x轴正半轴上运动时,点C随之在y轴正半轴上运动.
(1)当点A在原点时,求原点O到点B的距离OB.
(2)当OA
=
OC时,求原点O到点B的距离OB.
(3)求原点O到点B的距离OB的最大值,并确定此时图形应满足什么条件.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
