2020年秋浙教版九年级数学上册第3章《圆的基本性质》专训1 圆中常见的计算题型(Word版 含答案)
文档属性
| 名称 | 2020年秋浙教版九年级数学上册第3章《圆的基本性质》专训1 圆中常见的计算题型(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 425.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 10:52:38 | ||
图片预览


文档简介
专训1 圆中常见的计算题型
名师点金:
与圆有关的计算主要涉及圆与其他几何图形结合,利用圆周角定理求角度,利用垂径定理构造直角三角形并结合勾股定理,已知弦长、弦心距、半径三个量中的任意两个量时,可求出第三个量,利用弧长、扇形面积公式计算弧长、扇形面积等.
有关角度的计算
1.如图,⊙I是△ABC的内切圆,D,E,F为三个切点.若∠DEF=52°,则∠A的度数为( )
A.76°
B.68°
C.52°
D.38°
(第1题)
(第2题)
2.如图,有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点.若∠B=74°,∠C=46°,则所对圆心角的度数为( )
A.23°
B.28°
C.30°
D.37°
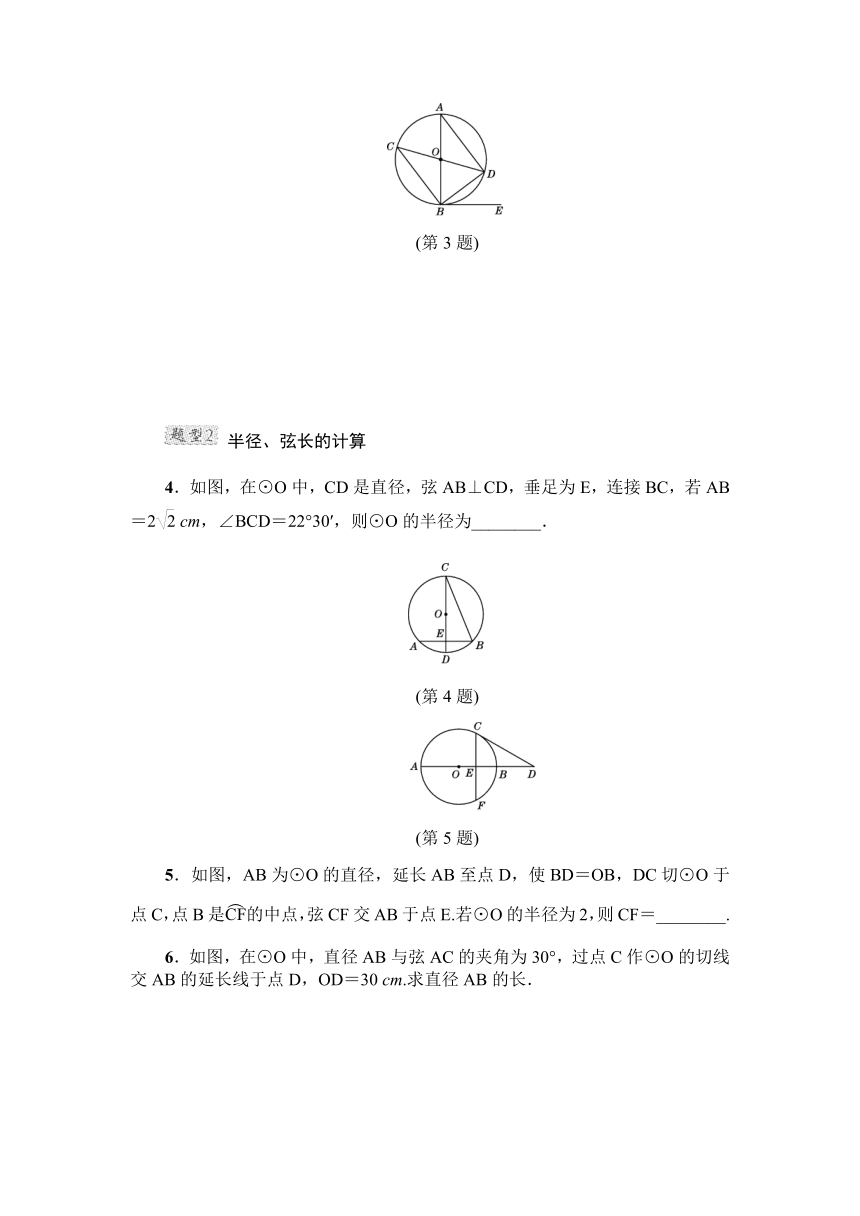
3.如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
(第3题)
半径、弦长的计算
4.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
cm,∠BCD=22°30′,则⊙O的半径为________.
(第4题)
(第5题)
5.如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=________.
6.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30
cm.求直径AB的长.
(第6题)
面积的计算
7.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
(第7题)
专训2 圆中常用的作辅助线的方法
名师点金:
在解决有关圆的计算或证明题时,往往需要添加辅助线,根据题目特点选择恰当的辅助线至关重要.圆中常用的辅助线作法有:作半径,巧用同圆的半径相等;连接圆上两点,巧用同弧所对的圆周角相等;作直径,巧用直径所对的圆周角是直角;证切线时“连半径,证垂直”以及“作垂直,证半径”等.
作半径,巧用同圆的半径相等
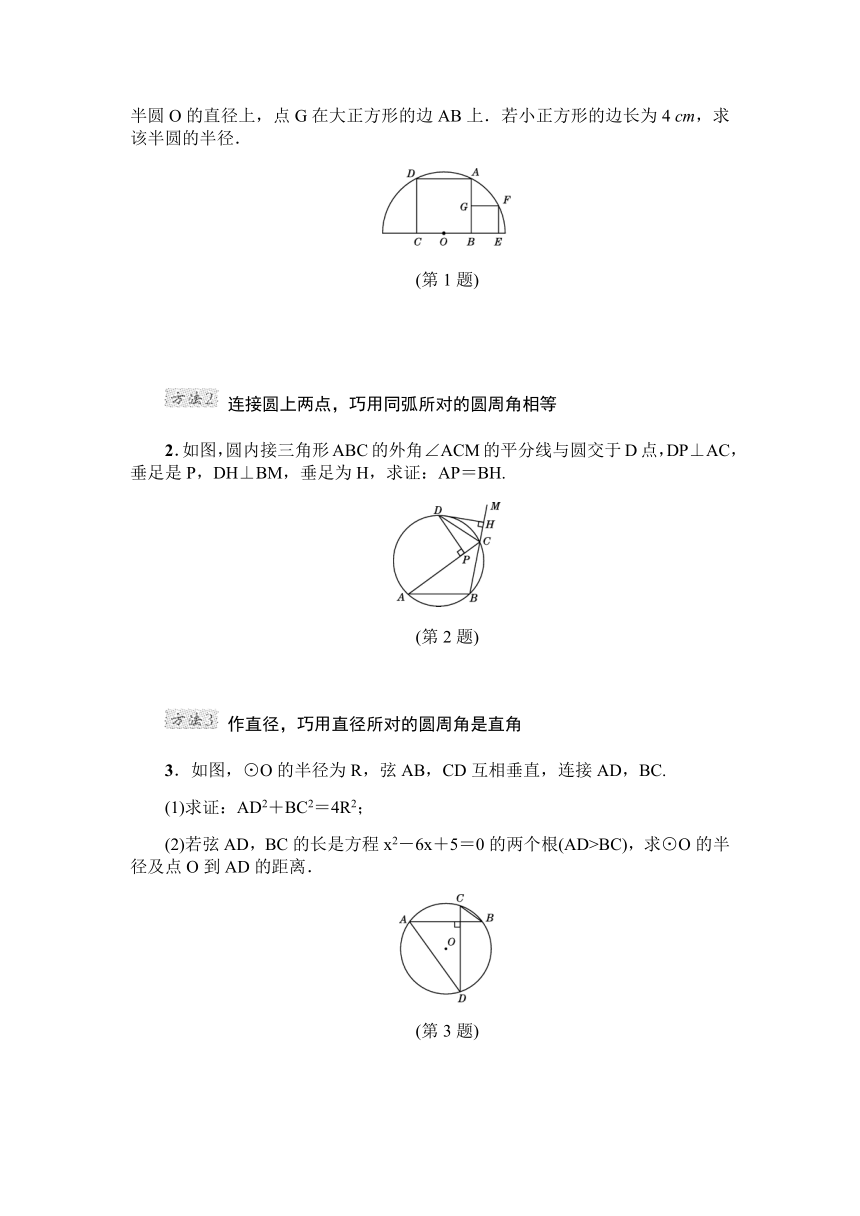
1.如图,两正方形彼此相邻,且大正方形ABCD的顶点A,D在半圆O上,顶点B,C在半圆O的直径上;小正方形BEFG的顶点F在半圆O上,E点在半圆O的直径上,点G在大正方形的边AB上.若小正方形的边长为4
cm,求该半圆的半径.
(第1题)
连接圆上两点,巧用同弧所对的圆周角相等
2.如图,圆内接三角形ABC的外角∠ACM的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BM,垂足为H,求证:AP=BH.
(第2题)
作直径,巧用直径所对的圆周角是直角
3.如图,⊙O的半径为R,弦AB,CD互相垂直,连接AD,BC.
(1)求证:AD2+BC2=4R2;
(2)若弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),求⊙O的半径及点O到AD的距离.
(第3题)
证切线时辅助线作法的应用
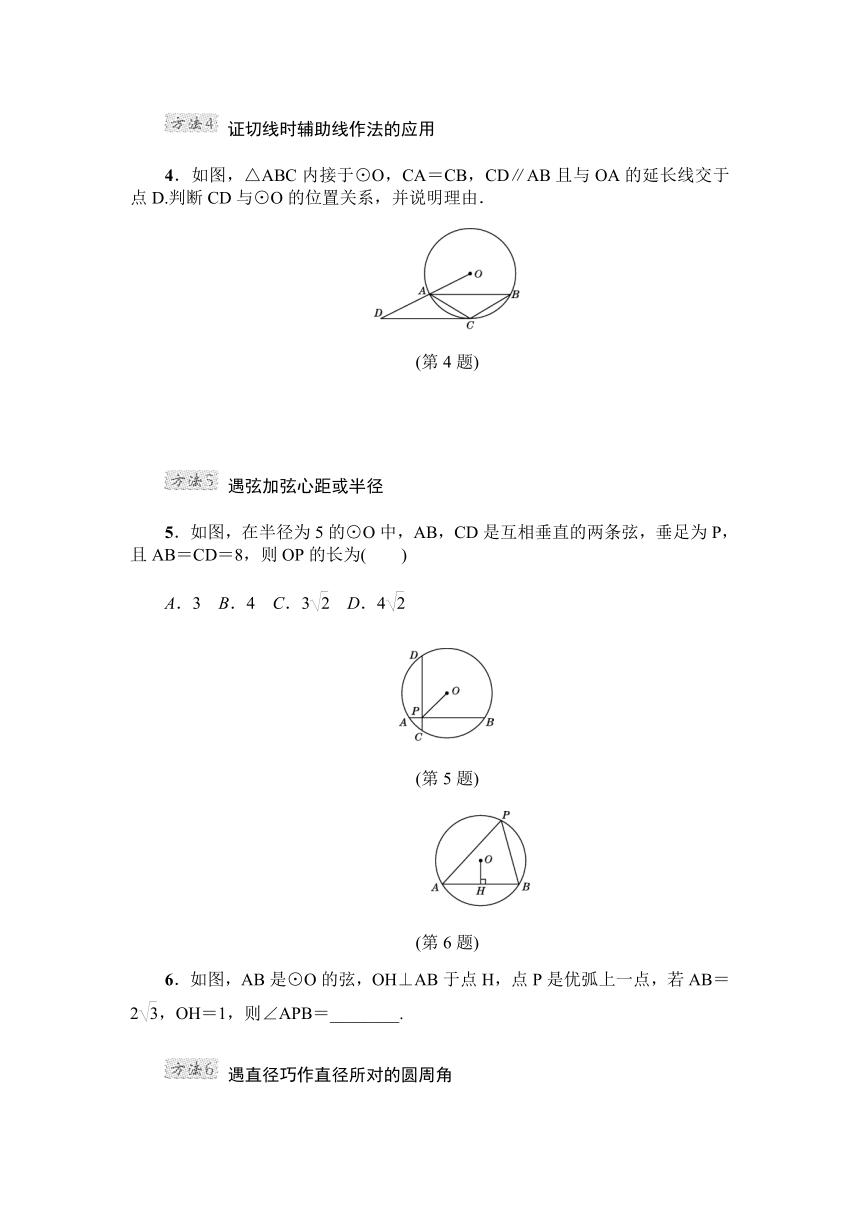
4.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.判断CD与⊙O的位置关系,并说明理由.
(第4题)
遇弦加弦心距或半径
5.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
(第5题)
(第6题)
6.如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2,OH=1,则∠APB=________.
遇直径巧作直径所对的圆周角
7.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
(第7题)
遇切线巧作过切点的半径
8.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=,∠ACB=60°,求⊙O的半径.
(第8题)
巧添辅助线计算阴影部分的面积
9.如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=6
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD,BD与所围成的阴影部分的面积(结果保留π).
(第9题)
专训3 圆的实际应用
名师点金:与圆有关的知识在实际生活中有着广泛的应用,从实际生活中抽象出数学问题,并运用圆的相关知识解决这些问题,可以达到学以致用的目的.
利用垂径定理解决台风问题
1.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30
km/h,受影响区域的半径为200
km,B市位于点P北偏东75°的方向上,距离P点320
km处.
(1)试说明台风是否会影响B市;
(2)若B市受台风的影响,求台风影响B市的时间.
(第1题)
利用圆周角知识解决足球射门问题(转化思想)
2.如图,在“世界杯”足球比赛中,队员甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴队员乙已经助攻冲到B点,现有两种射门方式:一是由队员甲直接射门;二是队员甲将球迅速传给队员乙,由队员乙射门.
从射门角度考虑,你认为选择哪种射门方式较好?为什么?
(第2题)
利用直线与圆的位置关系解决范围问题
3.已知A,B两地相距1
km.要在A,B两地之间修建一条笔直的水渠(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一个以C为圆心,350
m为半径的圆形公园,则修建的这条水渠会不会穿过公园?为什么?
(第3题)
利用圆锥侧面展开图解决材料最省问题
4.如图,某工厂要选一块矩形铁皮加工成一个底面半径为20
cm,高为40
cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
(第4题)
专训4 与圆有关的动态问题
名师点金:
对于与圆有关的运动情形下的几何问题,在探究求值问题时,通常应对运动过程中所有可能出现的不同情形进行分析,如果符合某些条件的点、线等几何图形不唯一,要注意分类讨论,在探究确定结论成立情况下的已知条件时,可以把确定结论当作已知用.
利用圆探究运动中形成的特殊几何图形问题
1.如图,AB是半圆O的直径,BC是弦,点P从点A开始,沿AB向点B以1
cm/s的速度移动,若AB长为10
cm,点O到BC的距离为4
cm.
(1)求弦BC的长;
(2)经过几秒△BPC是等腰三角形?(PB不能为底边)
(第1题)
2.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
(第2题)
利用圆探究运动中的特殊位置关系问题
3.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=12
cm,AD=8
cm,BC=22
cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1
cm/s的速度运动,动点Q从点C开始沿CB边向点B以2
cm/s的速度运动,P,Q分别从点A,C同时出发.当其中一动点到达终点时,另一个动点也随之停止运动.设运动时间为t
s.当t为何值时,PQ与⊙O相切?
(第3题)
利用圆探究运动中的面积问题
4.如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
(第4题)
专训5 几种常见的热门考点
名师点金:
圆的知识是初中数学的重点内容,也是历年中考命题的热点.本章题型广泛,主要考查圆的概念、基本性质以及圆周角定理及其推论,直线与圆的位置关系,切线的性质和判定,正多边形与圆的计算和证明等,通常以这些知识作为载体,与函数、方程等知识综合考查.
垂径定理及其推论的应用
1.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
(第1题)
(第2题)
2.如图是一圆柱形输水管的横截面,阴影部分为有水部分.如果水面AB的宽为8
cm,水的最大深度为2
cm,那么该输水管的半径为( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
圆心角与圆周角
3.如图所示,AB是⊙O的直径,AB⊥弦CD于点E,∠BOC=70°,则∠ABD=( )
A.20°
B.46°
C.55°
D.70°
(第3题)
(第4题)
4.如图,A,B,C,D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40°
B.45°
C.50°
D.55°
5.如图所示,C为半圆上一点,=,过点C作直径AB的垂线CP,P为垂足,弦AE交PC于点D,交CB于点F.求证:AD=CD.
(第5题)
点、直线与圆的位置关系
6.已知⊙O的半径为4
cm,A为线段OP的中点,当OP=7
cm时,点A与⊙O的位置关系是( )
A.点A在⊙O内
B.点A在⊙O上
C.点A在⊙O外
D.不能确定
7.在Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,以点C为圆心,r为半径作圆,若⊙C与直线AB相切,则r的值为( )
A.2
cm
B.2.4
cm
C.3
cm
D.4
cm
8.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程2x2-2x+m-1=0有实数根,则直线l与⊙O( )
A.相离或相切
B.相切或相交
C.相离或相交
D.无法确定
切线的判定与性质
(第9题)
9.如图,AB是⊙O的直径,AC是⊙O的切线,连结OC交⊙O于点D,连结BD,∠C=40°,则∠ABD的度数是( )
A.30°
B.25°
C.20°
D.15°
10.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E.
(1)若BC=,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证DF是⊙O的切线.
(第10题)
与圆有关的计算
11.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为( )
(第11题)
A.25π-6
B.π-6
C.π-6
D.π-6
12.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)
(第12题)
圆与其他知识的综合
圆与三角形的综合
13.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,连结BD.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由.
(第13题)
圆与四边形的综合
14.已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(1)如图①,求∠ADC的大小;
(2)如图②,经过点O作CD的平行线,与AB交于点E,与交于点F,连结AF,求∠FAB的大小.
(第14题)
圆与函数的综合
15.如图,直线y=-x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)如图①,当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径r;
(3)在⊙C的移动过程中,能否使△OEF是等边三角形?(只回答“能”或“不能”)
(第15题)
专训6 圆与二次函数的综合
名师点金:
圆与二次函数的综合,一般会涉及勾股定理、相似三角形的判定、求二次函数的表达式、求直线对应的函数表达式、切线的判定与性质,综合考察的知识点较多,同学们注意培养自己解答综合题的能力,关键还是基础知识的掌握,要能将所学知识融会贯通,有的问题的解法不止一种,同学们可以积极探索其他解法.
二次函数中利用全等证明圆与直线的位置关系
1.如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
(1)求经过B、C、D三点的抛物线对应的函数表达式;
(2)设抛物线的顶点为E,证明:直线CE与⊙A相切.
(第1题)
利用直线与圆的位置关系求直线对应的函数表达式
2.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).
(1)求抛物线对应的函数表达式;
(2)以AB为直径作⊙M,一直线经过点E(-1,-5),并且与⊙M相切,求该直线对应的函数表达式.
(第2题)
利用圆的有关性质求抛物线对应的函数表达式
3.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧ED上的点F作FH⊥AD于点H,且FH=1.5.
(1)求点D的坐标及该抛物线对应的函数表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标.
(第3题)
二次函数中利用勾股定理的逆定理证明直线与圆的位置关系
4.如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
(1)求D点的坐标和圆D的半径;
(2)求sin
∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;
(3)设抛物线的顶点为F,证明直线AF与圆D相切.
(第4题)
答案
1.A
2.B 点拨:∵有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点,∴所对的圆心角的度数=2∠C=2×46°=92°,所对的圆心角的度数=2∠B=2×74°=148°=所对的圆心角的度数+所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数+所对的圆心角的度数,∴所对的圆心角的度数=(148°-92°)=28°.故选B.
3.(1)证明:∵AB,CD是直径,∴∠ADB=∠CBD=90°.
在Rt△ABD和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL).
(2)解:∵BE是切线,∴AB⊥BE.∴∠ABE=90°.
∵∠DBE=37°,∴∠ABD=53°.
∵OD=OA,∴∠ODA=∠BAD=90°-53°=37°,
即∠ADC的度数为37°.
4.2
cm 点拨:连接OB,∵∠BCD=22°30′,∴∠BOD=2∠BCD=45°.∵AB⊥CD,∴BE=AE=AB=×2=(cm),△BOE为等腰直角三角形,∴OB=BE=2
cm,故答案为2
cm.
5.2
6.解:连接OC.∵∠A=30°,∴∠COD=60°.
∵DC切⊙O于C,∴∠OCD=90°.∴∠D=30°.
∵OD=30
cm,∴OC=OD=15
cm.
∴AB=2OC=30
cm.
(第7题)
7.(1)证明:如图,连接OD,
∵OB=OD,
∴∠ABC=∠ODB.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB.
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)解:如图,连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°.
∵OA=OE,∴∠AOE=90°.
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8.
∴S阴影=S扇形AOE-S△AOE=4π-8.
(第1题)
1.解:连接OA,OF,如图.设OA=OF=r
cm,AB=a
cm.
在Rt△OAB中,r2=+a2,
在Rt△OEF中,r2=42+,
∴+a2=16+16+4a+,解得a1=8,a2=-4(舍去).
∴r2=+82=80,∴r1=4,r2=-4(舍去),即该半圆的半径为4
cm.
点拨:在有关圆的计算题中,求角度或边长时,常连接半径构造等腰三角形或直角三角形,利用特殊三角形的性质来解决问题.
2.证明:连接AD,BD.∵∠DAC,∠DBC是所对的圆周角.
∴∠DAC=∠DBC.
∵CD平分∠ACM,DP⊥AC,DH⊥CM,∴DP=DH.
在△ADP和△BDH中,
∴△ADP≌△BDH,∴AP=BH.
点拨:本题通过作辅助线构造圆周角,然后利用“同弧所对的圆周角相等”得到∠DAC=∠DBC,为证两三角形全等创造了条件.
3.(1)证明:过点D作⊙O的直径DE,连接AE,EC,AC.
∵DE是⊙O的直径,∴∠ECD=∠EAD=90°.
又∵CD⊥AB,∴EC∥AB,
∴∠BAC=∠ACE.
∴=.∴BC=AE.
在Rt△AED中,AD2+AE2=DE2,
∴AD2+BC2=4R2.
(2)解:过点O作OF⊥AD于点F.
∵弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),
∴AD=5,BC=1.
由(1)知,AD2+BC2=4R2,
∴52+12=4R2,∴R=.
∵∠EAD=90°,OF⊥AD,∴OF∥EA.
又∵O为DE的中点,∴OF=AE=BC=,即点O到AD的距离为.
点拨:本题作出直径DE,利用“直径所对的圆周角是直角”构造了两个直角三角形,给解题带来了方便.
4.解:CD与⊙O相切,理由如下:如图,作直径CE,连接AE.
∵CE是直径,∴∠EAC=90°.
∴∠E+∠ACE=90°.
∵CA=CB,∴∠B=∠CAB.
∵AB∥CD,∴∠ACD=∠CAB.
∵∠B=∠E,∴∠ACD=∠E,
∴∠ACE+∠ACD=90°,即OC⊥DC.又OC为⊙O的半径,
∴CD与⊙O相切.
(第4题)
(第7题)
5.C 6.60°
7.(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵点D是BC的中点,∴AD是线段BC的垂直平分线,
∴AB=AC.
∵AB=BC,∴AB=BC=AC,
∴△ABC为等边三角形.
(2)解:连接BE.
∵AB是直径,∴∠AEB=90°,
∴BE⊥AC,
∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.
∵D是BC的中点,故DE为△ABC的中位线.
∴DE=AB=×2=1.
8.(1)证明:连接OB,∵OA=OB,∴∠OAB=∠OBA.
∵PA=PB,∴∠PAB=∠PBA.
∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO.
又∵PA是⊙O的切线,∴∠PAO=90°.∴∠PBO=90°.∴OB⊥PB.
又∵OB是⊙O的半径,∴PB是⊙O的切线.
(2)解:连接OP,
∵PA=PB,∴点P在线段AB的垂直平分线上.
∵OA=OB,∴点O在线段AB的垂直平分线上.
∴OP为线段AB的垂直平分线,
又∵BC⊥AB,∴PO∥BC.∴∠AOP=∠ACB=60°.∴∠OPA=30°.
在Rt△APO中,AO2+PA2=PO2,即AO2+3=(2AO)2.
又∵AO>0,
∴AO=1.∴⊙O的半径为1.
(第8题)
(第9题)
9.(1)证明:如图,连接CO,交DB于点E,∴∠O=2∠CDB=60°.
又∵∠OBE=30°,∴∠BEO=180°-60°-30°=90°.
∵AC∥BD,∴∠ACO=∠BEO=90°,即OC⊥AC.
又∵点C在⊙O上,∴AC是⊙O的切线.
(2)解:∵OE⊥DB,
∴EB=DB=3
cm.
在Rt△EOB中,
∵∠OBE=30°,∴OE=OB.
∵EB=3
cm,∴由勾股定理可求得OB=6
cm.
又∵∠D=∠DBO,DE=BE,∠CED=∠OEB,
∴△CDE≌△OBE,∴S△CDE=S△OBE,
∴S阴影=S扇形OCB=π·62=6π(cm2).
1.解:(1)如图,过B作BH⊥PQ于H,在Rt△BHP中,由条件易知:BP=320
km,∠BPQ=30°.∴BH=BP=160
km<200
km.∴台风会影响B市.
(2)如图,以B为圆心,200
km为半径作圆,交PQ于P1,P2两点,连接BP1,由垂径定理知P1P2=2P1H.
在Rt△BHP1中,BP1=200
km,
BH=160
km,
∴P1H==120(km).
∴P1P2=2P1H=240
km.
∴台风影响B市的时间为=8(h).
点拨:本题在图形中画出圆,可以非常直观地构造数学模型,然后利用垂径定理解决生活中的实际问题.
(第1题)
(第2题)
2.解:选择射门方式二较好,理由如下:设AQ与圆的交点为C,连接PC,如图所示.
∵∠PCQ是△PAC的外角,
∴∠PCQ>∠A.又∵∠PCQ=∠B,
∴∠B>∠A.∴在B点射门比在A点射门好.∴选择射门方式二较好.
点拨:本题运用转化思想,将射门角度大小的问题,建模转化到圆中,根据圆周角的相关知识来解决实际问题.
3.解:修建的这条水渠不会穿过公园.
理由:过点C作CD⊥AB,垂足为D.
∵∠CBA=45°,
∴∠BCD=45°,CD=BD.
设CD=x
km,则BD=x
km.
易知∠CAB=30°,∴AC=2x
km,AD==x
km.
∴x+x=1,解得x=,
即CD=
km≈0.366
km=366
m>350
m,
也就是说,以点C为圆心,350
m为半径的圆与AB相离.
即修建的这条水渠不会穿过公园.
4.解:∵圆锥形漏斗的底面半径为20
cm,高为40
cm,
∴圆锥的母线长为=60(cm).
设圆锥的侧面展开图的圆心角为n°,则有=2π×20,解得n=120.
方案一:如图①,扇形的半径为60
cm,矩形的宽为60
cm,易求得矩形的长为60
cm.
此时矩形的面积为60×60=3
600(cm2).
方案二:如图②,扇形与矩形的两边相切,有一边重合,易求得矩形的宽为60
cm,长为30+60=90(cm),此时矩形的面积为90×60=5
400(cm2).
∵3
600>5
400,
∴方案二所用材料最省,即选长为90
cm,宽为60
cm的矩形铁皮,才能使所用材料最省.
(第4题)
1.解:(1)作OD⊥BC于D.
由垂径定理知,点D是BC的中点,即BD=BC,∵OB=AB=5
cm,OD=4
cm,由勾股定理得,BD==3
cm,∴BC=2BD=6
cm.
(2)设经过t
s,△BPC是等腰三角形.
①当PC为底边时,有BP=BC,即10-t=6,解得t=4;
②当BC为底边时,有PC=PB,此时P点与O点重合,t=5.
∴经过4
s或5
s△BPC是等腰三角形.
2.解:(1)线段AB长度的最小值为4.
理由如下:连接OP.
∵AB切⊙O于P,∴OP⊥AB.
取AB的中点C,则AB=2OC,
当OC=OP时,OC最短,即AB最短,此时AB=4.
(2)存在.假设存在符合条件的点Q.
如图①,设四边形APOQ为平行四边形,
∵∠APO=90°,∴四边形APOQ为矩形.又∵OP=OQ,
∴四边形APOQ为正方形,
∴OQ=QA.∴∠QOA=45°,
在Rt△OQA中,根据OQ=2,∠AOQ=45°,
得Q点的坐标为(,-).
(第2题)
如图②,设四边形APQO为平行四边形,连接OP,
∵OQ∥PA,∠APO=90°,∴∠POQ=90°.
又∵OP=OQ,∴∠PQO=45°,
∵PQ∥OA,∴PQ⊥y轴.
设PQ交y轴于点H,
在Rt△OHQ中,根据OQ=2,∠HQO=45°,
得Q点的坐标为(-,).
∴符合条件的点Q的坐标为(,-)或(-,).
3.解:如图,设PQ与⊙O相切于点H,过点P作PE⊥BC,垂足为E.
(第3题)
∵在四边形ABCD中,AD∥BC,∠ABC=90°,
∴PE=AB.由题意可知:AP=BE=t
cm,CQ=2t
cm,
∴BQ=BC-CQ=(22-2t)
cm,EQ=BQ-BE=22-2t-t=(22-3t)
cm.
∵AB为⊙O的直径,∠ABC=∠DAB=90°,
∴AD,BC为⊙O的切线.∴AP=PH,HQ=BQ.
∴PQ=PH+HQ=AP+BQ=t+22-2t=(22-t)
cm.
在Rt△PEQ中,PE2+EQ2=PQ2,
∴122+(22-3t)2=(22-t)2,即
t2-11t+18=0,解得t1=2,t2=9.
∵P在AD边运动的时间为==8(s),而t=9>8,∴t=9(舍去).
∴当t=2
s时,PQ与⊙O相切.
4.解:(1)∵在△ACO中,∠OAC=60°,OC=OA,
∴△ACO是等边三角形.
∴∠AOC=60°.
(2)如图,
(第4题)
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°,
∴=×60=π.
∴当点M运动到M1时,S△MAO=S△CAO,
此时动点M经过的弧长为π.
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO,
∴∠OM1M2=∠AOM1=60°.
又∵OM1=OM2,∴∠M1OM2=60°,∴∠AOM2=120°.
∴=×120=π.
∴当点M运动到M2时,S△MAO=S△CAO,此时动点M经过的弧长为π.
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO,∠AOM3=120°.
∴=×240=π.
∴当点M运动到M3时,S△MAO=S△CAO,此时动点M经过的弧长为π.
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时动点M经过的弧长为×300=π.
综上所述,当S△MAO=S△CAO时,动点M所经过的弧长为π或π或π或π.
1.C 2.C 3.C 4.D
(第5题)
5.证明:如图,连结AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠DCB=90°.
∵CP⊥AB于点P,
∴∠B+∠DCB=90°,
∴∠ACD=∠B.
又∵=,∴∠B=∠CAD=∠ACD,∴AD=CD.
6.A 7.B 8.B 9.B
(第10题)
10.(1)解:设⊙O的半径为r,
∵AB是⊙O的直径,BC是⊙O的切线,
∴AB⊥BC,
在Rt△OBC中,∵OC2=OB2+CB2,
∴(r+1)2=r2+()2,
解得r=1,∴⊙O的半径为1.
(2)证明:连结OF,
∵OA=OB,BF=EF,
∴OF是△BAE的中位线,
∴OF∥AE,
∴∠A=∠2,∠1=∠ADO,
又∵∠ADO=∠A,∴∠1=∠2,
在△OBF和△ODF中,
∴△OBF≌△ODF,
∴∠ODF=∠OBF=90°,
即OD⊥DF,又OD是⊙O的半径,
∴FD是⊙O的切线.
11.D
(第12题)
12.解:(1)相切,理由如下:
如图,连结OD,
∵AD平分∠BAC,
∴∠1=∠2.
∵OA=OD,∴∠1=∠3,
∴∠2=∠3,∴OD∥AC.
又∠C=90°,∴OD⊥BC,
∴BC与⊙O相切.
(2)①设⊙O的半径为r.
∵AC=3,∠B=30°,∴AB=6.
又OA=OD=r,∴OB=2r.
∴2r+r=6,解得r=2,即⊙O的半径是2.
②由①得OD=2,则OB=4,BD=2,S阴影=S△OBD-S扇形ODE=×2×2-=2-.
13.(1)证明:在Rt△CED中,∠C+∠CED=90°,在Rt△BFE中,∠EFB+∠BEF=90°.∵∠CED=∠BEF,∴∠C=∠EFB.
在Rt△ABC和Rt△EBF中,
∴△ABC≌△EBF.
(2)解:BD与⊙O相切,理由如下:
连结BO,∵OB=OF,
∴∠OBF=∠OFB.
∵FD垂直平分AC,∴D为AC的中点,又∵△ABC为直角三角形.
∴BD=CD,
∴∠DCB=∠DBC.
由(1)知∠ACB=∠EFB,
∴∠DBC=∠DFB=∠OBF.
∵∠CBF=∠CBO+∠OBF=90°,
∴∠DBO=∠CBO+∠DBC=90°,
∴BD为⊙O的切线.
14.解:(1)∵CD是⊙O的切线,C为切点,
∴OC⊥CD,即∠OCD=90°.
∵四边形OABC是平行四边形,
(第14题)
∴AB∥OC,即AD∥OC.
∴∠ADC+∠OCD=180°,
∴∠ADC=180°-∠OCD=90°.
(2)如图,连结OB,则OB=OA=OC.
∵四边形OABC是平行四边形,
∴OC=AB,
∴OA=OB=AB.
即△AOB是等边三角形.
于是,∠AOB=60°.
由OF∥CD,又∠ADC=90°,得∠AEO=∠ADC=90°.
∴OF⊥AB,有=.
∴∠FOB=∠FOA=∠AOB=30°.
∴∠FAB=∠FOB=15°.
15.解:(1)∵直线y=-x+3与x轴交于点A(4,0),与y轴交于点B(0,3),∴OA=4,OB=3,∴AB==5.连结CF,∵四边形OBCE是矩形,∴CE=OB=3.设OE=x,则由切线长定理知AF=AE=x+4,
∴BF=x+4-5=x-1.在Rt△CBF中,
∵BC=OE=x,CF=CE=3,BF=x-1,BC2=CF2+BF2,∴x2=32+(x-1)2,解得x=5,即OE=5,∴点C的坐标为(-5,3).
(2)连结CE,CD,易知四边形CEOD是正方形,
∴OE=OD=r.由切线长定理知BF=BD=3-r,AE=AF,又∵AE=AO+OE=4+r,AF=AB+BF=5+3-r=8-r,∴4+r=8-r,∴r=2.
(3)不能.
1.(1)解:设过点B、C、D三点的抛物线对应的函数表达式为y=ax2+bx+c,则
解得
∴经过B、C、D三点的抛物线对应的函数表达式为y=x2+x+4.
(2)证明:∵y=x2+x+4=(x+5)2-,∴E.
设直线CE对应的函数表达式为y=mx+n,直线CE与y轴交于点G,则解得
∴直线CE对应的函数表达式为y=x+.
在y=x+中,当x=0时,y=,
∴点G的坐标为.
如图,连结AB、AC、AG,则
BG=OB-OG=4-=,CG===,
∴BG=CG.又∵AB=AC,AG=AG,
∴△ABG≌△ACG,
∴∠ACG=∠ABG.
∵⊙A与y轴相切于点B(0,4),
∴∠ABG=90°,
∴∠ACG=∠ABG=90°.
∵点C在⊙A上,∴直线CE与⊙A相切.
(第1题)
2.解:(1)∵抛物线过点A(-4,0),B(2,0),C(0,2).
∴解得
∴抛物线对应的函数表达式为y=-x2-x+2.
(第2题)
(2)如图,过E点作⊙M的切线,这样的切线共有2条.
当切点P在左半圆上时,连结MP,ME,过P作PH⊥x轴于点H.
∵A(-4,0),B(2,0),∴M(-1,0),⊙M的半径MP=MA=3.
又∵E(-1,-5),∴ME=5.
∴在Rt△MPE中,PE=4.
易得△HPM∽△PME,
∴PH∶PM=PM∶ME=HM∶PE,
∴PH=,HM=.
∴OH=.
∴
P.
∵直线过P,E(-1,-5),
设直线对应的函数表达式为y=kx+m(k≠0),
∴
解得
∴直线对应的函数表达式为
y=-x-.
同理,当切点在右半圆上时,可求得直线对应的函数表达式为y=x-.
综上所述,直线对应的函数表达式为y=-x-或y=x-.
3.解:(1)如图,连结BD,
∵AD是⊙M的直径,∴∠ABD=90°.
∴△AOB∽△ABD,
∴=.
在Rt△AOB中,AO=1,BO=2,
根据勾股定理得:AB=,
∴=,
∴AD=5,
∴DO=AD-AO=5-1=4,
∴D(4,0).
把点A(-1,0)、B(0,-2)、D(4,0)的坐标分别代入y=ax2+bx+c可得:
解得:
∴抛物线对应的函数表达式为:y=x2-x-2.
(第3题)
(2)如图,连结FM,BF.
在Rt△FHM中,FM=AD=,FH=,
∴MH==2,.
又∵OM=AM-OA=-1=,
∴OH=OM+MH=+2=,
∴F.
设直线BF对应的函数表达式为y=kx+m,
则:解得
∴直线BF对应的函数表达式为:y=x-2,
设BF交x轴于点P,易知点E与点B关于x轴对称,
∴点P即为所求,
当y=0时,x=2,
∴P(2,0).
4.(1)解:如图,连结DC,AD,则DC⊥y轴,
过点D作DE⊥AB于点E,则DE垂直平分AB,DE=OC=4.
∵AB=6,∴AE=3,
在Rt△ADE中,AD===5,
∴CD=5.
故点D的坐标为(5,4),圆的半径为5.
(第4题)
(2)解:在Rt△AOC中,OA=CD-AE=2,∴AC===2,
在Rt△BOC中,OB=OA+AB=8,
∴BC===4,
∵S△ABC=BC×ACsin∠ACB=AB×CO,
∴sin∠ACB==;
易得A、B的坐标分别为(2,0)、(8,0),设经过点A、B、C三点的抛物线对应的函数表达式为:y=ax2+bx+c,
将三点的坐标分别代入可得:
解得:
故经过C、A、B三点的抛物线对应的函数表达式为:y=x2-x+4.
(3)证明:如图,连结DF,
易得抛物线顶点坐标:F,DF=4-=,AF==,
∵DA2+AF2=52+===DF2,
∴∠DAF=90°.又∵A在圆D上,
∴直线AF与圆D相切
名师点金:
与圆有关的计算主要涉及圆与其他几何图形结合,利用圆周角定理求角度,利用垂径定理构造直角三角形并结合勾股定理,已知弦长、弦心距、半径三个量中的任意两个量时,可求出第三个量,利用弧长、扇形面积公式计算弧长、扇形面积等.
有关角度的计算
1.如图,⊙I是△ABC的内切圆,D,E,F为三个切点.若∠DEF=52°,则∠A的度数为( )
A.76°
B.68°
C.52°
D.38°
(第1题)
(第2题)
2.如图,有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点.若∠B=74°,∠C=46°,则所对圆心角的度数为( )
A.23°
B.28°
C.30°
D.37°
3.如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
(第3题)
半径、弦长的计算
4.如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2
cm,∠BCD=22°30′,则⊙O的半径为________.
(第4题)
(第5题)
5.如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=________.
6.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30
cm.求直径AB的长.
(第6题)
面积的计算
7.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
(第7题)
专训2 圆中常用的作辅助线的方法
名师点金:
在解决有关圆的计算或证明题时,往往需要添加辅助线,根据题目特点选择恰当的辅助线至关重要.圆中常用的辅助线作法有:作半径,巧用同圆的半径相等;连接圆上两点,巧用同弧所对的圆周角相等;作直径,巧用直径所对的圆周角是直角;证切线时“连半径,证垂直”以及“作垂直,证半径”等.
作半径,巧用同圆的半径相等
1.如图,两正方形彼此相邻,且大正方形ABCD的顶点A,D在半圆O上,顶点B,C在半圆O的直径上;小正方形BEFG的顶点F在半圆O上,E点在半圆O的直径上,点G在大正方形的边AB上.若小正方形的边长为4
cm,求该半圆的半径.
(第1题)
连接圆上两点,巧用同弧所对的圆周角相等
2.如图,圆内接三角形ABC的外角∠ACM的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BM,垂足为H,求证:AP=BH.
(第2题)
作直径,巧用直径所对的圆周角是直角
3.如图,⊙O的半径为R,弦AB,CD互相垂直,连接AD,BC.
(1)求证:AD2+BC2=4R2;
(2)若弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),求⊙O的半径及点O到AD的距离.
(第3题)
证切线时辅助线作法的应用
4.如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交于点D.判断CD与⊙O的位置关系,并说明理由.
(第4题)
遇弦加弦心距或半径
5.如图,在半径为5的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
A.3
B.4
C.3
D.4
(第5题)
(第6题)
6.如图,AB是⊙O的弦,OH⊥AB于点H,点P是优弧上一点,若AB=2,OH=1,则∠APB=________.
遇直径巧作直径所对的圆周角
7.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D是BC的中点.
(1)求证:△ABC为等边三角形.
(2)求DE的长.
(第7题)
遇切线巧作过切点的半径
8.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=,∠ACB=60°,求⊙O的半径.
(第8题)
巧添辅助线计算阴影部分的面积
9.如图,点B,C,D都在⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=6
cm.
(1)求证:AC是⊙O的切线;
(2)求由弦CD,BD与所围成的阴影部分的面积(结果保留π).
(第9题)
专训3 圆的实际应用
名师点金:与圆有关的知识在实际生活中有着广泛的应用,从实际生活中抽象出数学问题,并运用圆的相关知识解决这些问题,可以达到学以致用的目的.
利用垂径定理解决台风问题
1.如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30
km/h,受影响区域的半径为200
km,B市位于点P北偏东75°的方向上,距离P点320
km处.
(1)试说明台风是否会影响B市;
(2)若B市受台风的影响,求台风影响B市的时间.
(第1题)
利用圆周角知识解决足球射门问题(转化思想)
2.如图,在“世界杯”足球比赛中,队员甲带球向对方球门PQ进攻,当他带球冲到A点时,同伴队员乙已经助攻冲到B点,现有两种射门方式:一是由队员甲直接射门;二是队员甲将球迅速传给队员乙,由队员乙射门.
从射门角度考虑,你认为选择哪种射门方式较好?为什么?
(第2题)
利用直线与圆的位置关系解决范围问题
3.已知A,B两地相距1
km.要在A,B两地之间修建一条笔直的水渠(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一个以C为圆心,350
m为半径的圆形公园,则修建的这条水渠会不会穿过公园?为什么?
(第3题)
利用圆锥侧面展开图解决材料最省问题
4.如图,某工厂要选一块矩形铁皮加工成一个底面半径为20
cm,高为40
cm的圆锥形漏斗,要求只能有一条接缝(接缝忽略不计),请问:选长、宽分别为多少厘米的矩形铁皮,才能使所用材料最省?
(第4题)
专训4 与圆有关的动态问题
名师点金:
对于与圆有关的运动情形下的几何问题,在探究求值问题时,通常应对运动过程中所有可能出现的不同情形进行分析,如果符合某些条件的点、线等几何图形不唯一,要注意分类讨论,在探究确定结论成立情况下的已知条件时,可以把确定结论当作已知用.
利用圆探究运动中形成的特殊几何图形问题
1.如图,AB是半圆O的直径,BC是弦,点P从点A开始,沿AB向点B以1
cm/s的速度移动,若AB长为10
cm,点O到BC的距离为4
cm.
(1)求弦BC的长;
(2)经过几秒△BPC是等腰三角形?(PB不能为底边)
(第1题)
2.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
(第2题)
利用圆探究运动中的特殊位置关系问题
3.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=12
cm,AD=8
cm,BC=22
cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1
cm/s的速度运动,动点Q从点C开始沿CB边向点B以2
cm/s的速度运动,P,Q分别从点A,C同时出发.当其中一动点到达终点时,另一个动点也随之停止运动.设运动时间为t
s.当t为何值时,PQ与⊙O相切?
(第3题)
利用圆探究运动中的面积问题
4.如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
(第4题)
专训5 几种常见的热门考点
名师点金:
圆的知识是初中数学的重点内容,也是历年中考命题的热点.本章题型广泛,主要考查圆的概念、基本性质以及圆周角定理及其推论,直线与圆的位置关系,切线的性质和判定,正多边形与圆的计算和证明等,通常以这些知识作为载体,与函数、方程等知识综合考查.
垂径定理及其推论的应用
1.如图所示,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
(第1题)
(第2题)
2.如图是一圆柱形输水管的横截面,阴影部分为有水部分.如果水面AB的宽为8
cm,水的最大深度为2
cm,那么该输水管的半径为( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
圆心角与圆周角
3.如图所示,AB是⊙O的直径,AB⊥弦CD于点E,∠BOC=70°,则∠ABD=( )
A.20°
B.46°
C.55°
D.70°
(第3题)
(第4题)
4.如图,A,B,C,D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40°
B.45°
C.50°
D.55°
5.如图所示,C为半圆上一点,=,过点C作直径AB的垂线CP,P为垂足,弦AE交PC于点D,交CB于点F.求证:AD=CD.
(第5题)
点、直线与圆的位置关系
6.已知⊙O的半径为4
cm,A为线段OP的中点,当OP=7
cm时,点A与⊙O的位置关系是( )
A.点A在⊙O内
B.点A在⊙O上
C.点A在⊙O外
D.不能确定
7.在Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,以点C为圆心,r为半径作圆,若⊙C与直线AB相切,则r的值为( )
A.2
cm
B.2.4
cm
C.3
cm
D.4
cm
8.设⊙O的半径为2,圆心O到直线l的距离OP=m,且m使得关于x的方程2x2-2x+m-1=0有实数根,则直线l与⊙O( )
A.相离或相切
B.相切或相交
C.相离或相交
D.无法确定
切线的判定与性质
(第9题)
9.如图,AB是⊙O的直径,AC是⊙O的切线,连结OC交⊙O于点D,连结BD,∠C=40°,则∠ABD的度数是( )
A.30°
B.25°
C.20°
D.15°
10.如图,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E.
(1)若BC=,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证DF是⊙O的切线.
(第10题)
与圆有关的计算
11.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为( )
(第11题)
A.25π-6
B.π-6
C.π-6
D.π-6
12.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°,
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和π)
(第12题)
圆与其他知识的综合
圆与三角形的综合
13.如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,连结BD.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由.
(第13题)
圆与四边形的综合
14.已知A,B,C是⊙O上的三个点,四边形OABC是平行四边形,过点C作⊙O的切线,交AB的延长线于点D.
(1)如图①,求∠ADC的大小;
(2)如图②,经过点O作CD的平行线,与AB交于点E,与交于点F,连结AF,求∠FAB的大小.
(第14题)
圆与函数的综合
15.如图,直线y=-x+3与x轴相交于点A,与y轴相交于点B,点C是第二象限内任意一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)如图①,当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径r;
(3)在⊙C的移动过程中,能否使△OEF是等边三角形?(只回答“能”或“不能”)
(第15题)
专训6 圆与二次函数的综合
名师点金:
圆与二次函数的综合,一般会涉及勾股定理、相似三角形的判定、求二次函数的表达式、求直线对应的函数表达式、切线的判定与性质,综合考察的知识点较多,同学们注意培养自己解答综合题的能力,关键还是基础知识的掌握,要能将所学知识融会贯通,有的问题的解法不止一种,同学们可以积极探索其他解法.
二次函数中利用全等证明圆与直线的位置关系
1.如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
(1)求经过B、C、D三点的抛物线对应的函数表达式;
(2)设抛物线的顶点为E,证明:直线CE与⊙A相切.
(第1题)
利用直线与圆的位置关系求直线对应的函数表达式
2.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-4,0),B(2,0),与y轴交于点C(0,2).
(1)求抛物线对应的函数表达式;
(2)以AB为直径作⊙M,一直线经过点E(-1,-5),并且与⊙M相切,求该直线对应的函数表达式.
(第2题)
利用圆的有关性质求抛物线对应的函数表达式
3.如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧ED上的点F作FH⊥AD于点H,且FH=1.5.
(1)求点D的坐标及该抛物线对应的函数表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标.
(第3题)
二次函数中利用勾股定理的逆定理证明直线与圆的位置关系
4.如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
(1)求D点的坐标和圆D的半径;
(2)求sin
∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;
(3)设抛物线的顶点为F,证明直线AF与圆D相切.
(第4题)
答案
1.A
2.B 点拨:∵有一圆经过△ABC的三个顶点,且弦BC的中垂线与相交于D点,∴所对的圆心角的度数=2∠C=2×46°=92°,所对的圆心角的度数=2∠B=2×74°=148°=所对的圆心角的度数+所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数=所对的圆心角的度数+所对的圆心角的度数+所对的圆心角的度数,∴所对的圆心角的度数=(148°-92°)=28°.故选B.
3.(1)证明:∵AB,CD是直径,∴∠ADB=∠CBD=90°.
在Rt△ABD和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL).
(2)解:∵BE是切线,∴AB⊥BE.∴∠ABE=90°.
∵∠DBE=37°,∴∠ABD=53°.
∵OD=OA,∴∠ODA=∠BAD=90°-53°=37°,
即∠ADC的度数为37°.
4.2
cm 点拨:连接OB,∵∠BCD=22°30′,∴∠BOD=2∠BCD=45°.∵AB⊥CD,∴BE=AE=AB=×2=(cm),△BOE为等腰直角三角形,∴OB=BE=2
cm,故答案为2
cm.
5.2
6.解:连接OC.∵∠A=30°,∴∠COD=60°.
∵DC切⊙O于C,∴∠OCD=90°.∴∠D=30°.
∵OD=30
cm,∴OC=OD=15
cm.
∴AB=2OC=30
cm.
(第7题)
7.(1)证明:如图,连接OD,
∵OB=OD,
∴∠ABC=∠ODB.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ODB=∠ACB.
∴OD∥AC.
∵DF是⊙O的切线,
∴DF⊥OD.
∴DF⊥AC.
(2)解:如图,连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°.
∵OA=OE,∴∠AOE=90°.
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8.
∴S阴影=S扇形AOE-S△AOE=4π-8.
(第1题)
1.解:连接OA,OF,如图.设OA=OF=r
cm,AB=a
cm.
在Rt△OAB中,r2=+a2,
在Rt△OEF中,r2=42+,
∴+a2=16+16+4a+,解得a1=8,a2=-4(舍去).
∴r2=+82=80,∴r1=4,r2=-4(舍去),即该半圆的半径为4
cm.
点拨:在有关圆的计算题中,求角度或边长时,常连接半径构造等腰三角形或直角三角形,利用特殊三角形的性质来解决问题.
2.证明:连接AD,BD.∵∠DAC,∠DBC是所对的圆周角.
∴∠DAC=∠DBC.
∵CD平分∠ACM,DP⊥AC,DH⊥CM,∴DP=DH.
在△ADP和△BDH中,
∴△ADP≌△BDH,∴AP=BH.
点拨:本题通过作辅助线构造圆周角,然后利用“同弧所对的圆周角相等”得到∠DAC=∠DBC,为证两三角形全等创造了条件.
3.(1)证明:过点D作⊙O的直径DE,连接AE,EC,AC.
∵DE是⊙O的直径,∴∠ECD=∠EAD=90°.
又∵CD⊥AB,∴EC∥AB,
∴∠BAC=∠ACE.
∴=.∴BC=AE.
在Rt△AED中,AD2+AE2=DE2,
∴AD2+BC2=4R2.
(2)解:过点O作OF⊥AD于点F.
∵弦AD,BC的长是方程x2-6x+5=0的两个根(AD>BC),
∴AD=5,BC=1.
由(1)知,AD2+BC2=4R2,
∴52+12=4R2,∴R=.
∵∠EAD=90°,OF⊥AD,∴OF∥EA.
又∵O为DE的中点,∴OF=AE=BC=,即点O到AD的距离为.
点拨:本题作出直径DE,利用“直径所对的圆周角是直角”构造了两个直角三角形,给解题带来了方便.
4.解:CD与⊙O相切,理由如下:如图,作直径CE,连接AE.
∵CE是直径,∴∠EAC=90°.
∴∠E+∠ACE=90°.
∵CA=CB,∴∠B=∠CAB.
∵AB∥CD,∴∠ACD=∠CAB.
∵∠B=∠E,∴∠ACD=∠E,
∴∠ACE+∠ACD=90°,即OC⊥DC.又OC为⊙O的半径,
∴CD与⊙O相切.
(第4题)
(第7题)
5.C 6.60°
7.(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵点D是BC的中点,∴AD是线段BC的垂直平分线,
∴AB=AC.
∵AB=BC,∴AB=BC=AC,
∴△ABC为等边三角形.
(2)解:连接BE.
∵AB是直径,∴∠AEB=90°,
∴BE⊥AC,
∵△ABC是等边三角形,∴AE=EC,即E为AC的中点.
∵D是BC的中点,故DE为△ABC的中位线.
∴DE=AB=×2=1.
8.(1)证明:连接OB,∵OA=OB,∴∠OAB=∠OBA.
∵PA=PB,∴∠PAB=∠PBA.
∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO.
又∵PA是⊙O的切线,∴∠PAO=90°.∴∠PBO=90°.∴OB⊥PB.
又∵OB是⊙O的半径,∴PB是⊙O的切线.
(2)解:连接OP,
∵PA=PB,∴点P在线段AB的垂直平分线上.
∵OA=OB,∴点O在线段AB的垂直平分线上.
∴OP为线段AB的垂直平分线,
又∵BC⊥AB,∴PO∥BC.∴∠AOP=∠ACB=60°.∴∠OPA=30°.
在Rt△APO中,AO2+PA2=PO2,即AO2+3=(2AO)2.
又∵AO>0,
∴AO=1.∴⊙O的半径为1.
(第8题)
(第9题)
9.(1)证明:如图,连接CO,交DB于点E,∴∠O=2∠CDB=60°.
又∵∠OBE=30°,∴∠BEO=180°-60°-30°=90°.
∵AC∥BD,∴∠ACO=∠BEO=90°,即OC⊥AC.
又∵点C在⊙O上,∴AC是⊙O的切线.
(2)解:∵OE⊥DB,
∴EB=DB=3
cm.
在Rt△EOB中,
∵∠OBE=30°,∴OE=OB.
∵EB=3
cm,∴由勾股定理可求得OB=6
cm.
又∵∠D=∠DBO,DE=BE,∠CED=∠OEB,
∴△CDE≌△OBE,∴S△CDE=S△OBE,
∴S阴影=S扇形OCB=π·62=6π(cm2).
1.解:(1)如图,过B作BH⊥PQ于H,在Rt△BHP中,由条件易知:BP=320
km,∠BPQ=30°.∴BH=BP=160
km<200
km.∴台风会影响B市.
(2)如图,以B为圆心,200
km为半径作圆,交PQ于P1,P2两点,连接BP1,由垂径定理知P1P2=2P1H.
在Rt△BHP1中,BP1=200
km,
BH=160
km,
∴P1H==120(km).
∴P1P2=2P1H=240
km.
∴台风影响B市的时间为=8(h).
点拨:本题在图形中画出圆,可以非常直观地构造数学模型,然后利用垂径定理解决生活中的实际问题.
(第1题)
(第2题)
2.解:选择射门方式二较好,理由如下:设AQ与圆的交点为C,连接PC,如图所示.
∵∠PCQ是△PAC的外角,
∴∠PCQ>∠A.又∵∠PCQ=∠B,
∴∠B>∠A.∴在B点射门比在A点射门好.∴选择射门方式二较好.
点拨:本题运用转化思想,将射门角度大小的问题,建模转化到圆中,根据圆周角的相关知识来解决实际问题.
3.解:修建的这条水渠不会穿过公园.
理由:过点C作CD⊥AB,垂足为D.
∵∠CBA=45°,
∴∠BCD=45°,CD=BD.
设CD=x
km,则BD=x
km.
易知∠CAB=30°,∴AC=2x
km,AD==x
km.
∴x+x=1,解得x=,
即CD=
km≈0.366
km=366
m>350
m,
也就是说,以点C为圆心,350
m为半径的圆与AB相离.
即修建的这条水渠不会穿过公园.
4.解:∵圆锥形漏斗的底面半径为20
cm,高为40
cm,
∴圆锥的母线长为=60(cm).
设圆锥的侧面展开图的圆心角为n°,则有=2π×20,解得n=120.
方案一:如图①,扇形的半径为60
cm,矩形的宽为60
cm,易求得矩形的长为60
cm.
此时矩形的面积为60×60=3
600(cm2).
方案二:如图②,扇形与矩形的两边相切,有一边重合,易求得矩形的宽为60
cm,长为30+60=90(cm),此时矩形的面积为90×60=5
400(cm2).
∵3
600>5
400,
∴方案二所用材料最省,即选长为90
cm,宽为60
cm的矩形铁皮,才能使所用材料最省.
(第4题)
1.解:(1)作OD⊥BC于D.
由垂径定理知,点D是BC的中点,即BD=BC,∵OB=AB=5
cm,OD=4
cm,由勾股定理得,BD==3
cm,∴BC=2BD=6
cm.
(2)设经过t
s,△BPC是等腰三角形.
①当PC为底边时,有BP=BC,即10-t=6,解得t=4;
②当BC为底边时,有PC=PB,此时P点与O点重合,t=5.
∴经过4
s或5
s△BPC是等腰三角形.
2.解:(1)线段AB长度的最小值为4.
理由如下:连接OP.
∵AB切⊙O于P,∴OP⊥AB.
取AB的中点C,则AB=2OC,
当OC=OP时,OC最短,即AB最短,此时AB=4.
(2)存在.假设存在符合条件的点Q.
如图①,设四边形APOQ为平行四边形,
∵∠APO=90°,∴四边形APOQ为矩形.又∵OP=OQ,
∴四边形APOQ为正方形,
∴OQ=QA.∴∠QOA=45°,
在Rt△OQA中,根据OQ=2,∠AOQ=45°,
得Q点的坐标为(,-).
(第2题)
如图②,设四边形APQO为平行四边形,连接OP,
∵OQ∥PA,∠APO=90°,∴∠POQ=90°.
又∵OP=OQ,∴∠PQO=45°,
∵PQ∥OA,∴PQ⊥y轴.
设PQ交y轴于点H,
在Rt△OHQ中,根据OQ=2,∠HQO=45°,
得Q点的坐标为(-,).
∴符合条件的点Q的坐标为(,-)或(-,).
3.解:如图,设PQ与⊙O相切于点H,过点P作PE⊥BC,垂足为E.
(第3题)
∵在四边形ABCD中,AD∥BC,∠ABC=90°,
∴PE=AB.由题意可知:AP=BE=t
cm,CQ=2t
cm,
∴BQ=BC-CQ=(22-2t)
cm,EQ=BQ-BE=22-2t-t=(22-3t)
cm.
∵AB为⊙O的直径,∠ABC=∠DAB=90°,
∴AD,BC为⊙O的切线.∴AP=PH,HQ=BQ.
∴PQ=PH+HQ=AP+BQ=t+22-2t=(22-t)
cm.
在Rt△PEQ中,PE2+EQ2=PQ2,
∴122+(22-3t)2=(22-t)2,即
t2-11t+18=0,解得t1=2,t2=9.
∵P在AD边运动的时间为==8(s),而t=9>8,∴t=9(舍去).
∴当t=2
s时,PQ与⊙O相切.
4.解:(1)∵在△ACO中,∠OAC=60°,OC=OA,
∴△ACO是等边三角形.
∴∠AOC=60°.
(2)如图,
(第4题)
①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°,
∴=×60=π.
∴当点M运动到M1时,S△MAO=S△CAO,
此时动点M经过的弧长为π.
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO,
∴∠OM1M2=∠AOM1=60°.
又∵OM1=OM2,∴∠M1OM2=60°,∴∠AOM2=120°.
∴=×120=π.
∴当点M运动到M2时,S△MAO=S△CAO,此时动点M经过的弧长为π.
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO,∠AOM3=120°.
∴=×240=π.
∴当点M运动到M3时,S△MAO=S△CAO,此时动点M经过的弧长为π.
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时动点M经过的弧长为×300=π.
综上所述,当S△MAO=S△CAO时,动点M所经过的弧长为π或π或π或π.
1.C 2.C 3.C 4.D
(第5题)
5.证明:如图,连结AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠DCB=90°.
∵CP⊥AB于点P,
∴∠B+∠DCB=90°,
∴∠ACD=∠B.
又∵=,∴∠B=∠CAD=∠ACD,∴AD=CD.
6.A 7.B 8.B 9.B
(第10题)
10.(1)解:设⊙O的半径为r,
∵AB是⊙O的直径,BC是⊙O的切线,
∴AB⊥BC,
在Rt△OBC中,∵OC2=OB2+CB2,
∴(r+1)2=r2+()2,
解得r=1,∴⊙O的半径为1.
(2)证明:连结OF,
∵OA=OB,BF=EF,
∴OF是△BAE的中位线,
∴OF∥AE,
∴∠A=∠2,∠1=∠ADO,
又∵∠ADO=∠A,∴∠1=∠2,
在△OBF和△ODF中,
∴△OBF≌△ODF,
∴∠ODF=∠OBF=90°,
即OD⊥DF,又OD是⊙O的半径,
∴FD是⊙O的切线.
11.D
(第12题)
12.解:(1)相切,理由如下:
如图,连结OD,
∵AD平分∠BAC,
∴∠1=∠2.
∵OA=OD,∴∠1=∠3,
∴∠2=∠3,∴OD∥AC.
又∠C=90°,∴OD⊥BC,
∴BC与⊙O相切.
(2)①设⊙O的半径为r.
∵AC=3,∠B=30°,∴AB=6.
又OA=OD=r,∴OB=2r.
∴2r+r=6,解得r=2,即⊙O的半径是2.
②由①得OD=2,则OB=4,BD=2,S阴影=S△OBD-S扇形ODE=×2×2-=2-.
13.(1)证明:在Rt△CED中,∠C+∠CED=90°,在Rt△BFE中,∠EFB+∠BEF=90°.∵∠CED=∠BEF,∴∠C=∠EFB.
在Rt△ABC和Rt△EBF中,
∴△ABC≌△EBF.
(2)解:BD与⊙O相切,理由如下:
连结BO,∵OB=OF,
∴∠OBF=∠OFB.
∵FD垂直平分AC,∴D为AC的中点,又∵△ABC为直角三角形.
∴BD=CD,
∴∠DCB=∠DBC.
由(1)知∠ACB=∠EFB,
∴∠DBC=∠DFB=∠OBF.
∵∠CBF=∠CBO+∠OBF=90°,
∴∠DBO=∠CBO+∠DBC=90°,
∴BD为⊙O的切线.
14.解:(1)∵CD是⊙O的切线,C为切点,
∴OC⊥CD,即∠OCD=90°.
∵四边形OABC是平行四边形,
(第14题)
∴AB∥OC,即AD∥OC.
∴∠ADC+∠OCD=180°,
∴∠ADC=180°-∠OCD=90°.
(2)如图,连结OB,则OB=OA=OC.
∵四边形OABC是平行四边形,
∴OC=AB,
∴OA=OB=AB.
即△AOB是等边三角形.
于是,∠AOB=60°.
由OF∥CD,又∠ADC=90°,得∠AEO=∠ADC=90°.
∴OF⊥AB,有=.
∴∠FOB=∠FOA=∠AOB=30°.
∴∠FAB=∠FOB=15°.
15.解:(1)∵直线y=-x+3与x轴交于点A(4,0),与y轴交于点B(0,3),∴OA=4,OB=3,∴AB==5.连结CF,∵四边形OBCE是矩形,∴CE=OB=3.设OE=x,则由切线长定理知AF=AE=x+4,
∴BF=x+4-5=x-1.在Rt△CBF中,
∵BC=OE=x,CF=CE=3,BF=x-1,BC2=CF2+BF2,∴x2=32+(x-1)2,解得x=5,即OE=5,∴点C的坐标为(-5,3).
(2)连结CE,CD,易知四边形CEOD是正方形,
∴OE=OD=r.由切线长定理知BF=BD=3-r,AE=AF,又∵AE=AO+OE=4+r,AF=AB+BF=5+3-r=8-r,∴4+r=8-r,∴r=2.
(3)不能.
1.(1)解:设过点B、C、D三点的抛物线对应的函数表达式为y=ax2+bx+c,则
解得
∴经过B、C、D三点的抛物线对应的函数表达式为y=x2+x+4.
(2)证明:∵y=x2+x+4=(x+5)2-,∴E.
设直线CE对应的函数表达式为y=mx+n,直线CE与y轴交于点G,则解得
∴直线CE对应的函数表达式为y=x+.
在y=x+中,当x=0时,y=,
∴点G的坐标为.
如图,连结AB、AC、AG,则
BG=OB-OG=4-=,CG===,
∴BG=CG.又∵AB=AC,AG=AG,
∴△ABG≌△ACG,
∴∠ACG=∠ABG.
∵⊙A与y轴相切于点B(0,4),
∴∠ABG=90°,
∴∠ACG=∠ABG=90°.
∵点C在⊙A上,∴直线CE与⊙A相切.
(第1题)
2.解:(1)∵抛物线过点A(-4,0),B(2,0),C(0,2).
∴解得
∴抛物线对应的函数表达式为y=-x2-x+2.
(第2题)
(2)如图,过E点作⊙M的切线,这样的切线共有2条.
当切点P在左半圆上时,连结MP,ME,过P作PH⊥x轴于点H.
∵A(-4,0),B(2,0),∴M(-1,0),⊙M的半径MP=MA=3.
又∵E(-1,-5),∴ME=5.
∴在Rt△MPE中,PE=4.
易得△HPM∽△PME,
∴PH∶PM=PM∶ME=HM∶PE,
∴PH=,HM=.
∴OH=.
∴
P.
∵直线过P,E(-1,-5),
设直线对应的函数表达式为y=kx+m(k≠0),
∴
解得
∴直线对应的函数表达式为
y=-x-.
同理,当切点在右半圆上时,可求得直线对应的函数表达式为y=x-.
综上所述,直线对应的函数表达式为y=-x-或y=x-.
3.解:(1)如图,连结BD,
∵AD是⊙M的直径,∴∠ABD=90°.
∴△AOB∽△ABD,
∴=.
在Rt△AOB中,AO=1,BO=2,
根据勾股定理得:AB=,
∴=,
∴AD=5,
∴DO=AD-AO=5-1=4,
∴D(4,0).
把点A(-1,0)、B(0,-2)、D(4,0)的坐标分别代入y=ax2+bx+c可得:
解得:
∴抛物线对应的函数表达式为:y=x2-x-2.
(第3题)
(2)如图,连结FM,BF.
在Rt△FHM中,FM=AD=,FH=,
∴MH==2,.
又∵OM=AM-OA=-1=,
∴OH=OM+MH=+2=,
∴F.
设直线BF对应的函数表达式为y=kx+m,
则:解得
∴直线BF对应的函数表达式为:y=x-2,
设BF交x轴于点P,易知点E与点B关于x轴对称,
∴点P即为所求,
当y=0时,x=2,
∴P(2,0).
4.(1)解:如图,连结DC,AD,则DC⊥y轴,
过点D作DE⊥AB于点E,则DE垂直平分AB,DE=OC=4.
∵AB=6,∴AE=3,
在Rt△ADE中,AD===5,
∴CD=5.
故点D的坐标为(5,4),圆的半径为5.
(第4题)
(2)解:在Rt△AOC中,OA=CD-AE=2,∴AC===2,
在Rt△BOC中,OB=OA+AB=8,
∴BC===4,
∵S△ABC=BC×ACsin∠ACB=AB×CO,
∴sin∠ACB==;
易得A、B的坐标分别为(2,0)、(8,0),设经过点A、B、C三点的抛物线对应的函数表达式为:y=ax2+bx+c,
将三点的坐标分别代入可得:
解得:
故经过C、A、B三点的抛物线对应的函数表达式为:y=x2-x+4.
(3)证明:如图,连结DF,
易得抛物线顶点坐标:F,DF=4-=,AF==,
∵DA2+AF2=52+===DF2,
∴∠DAF=90°.又∵A在圆D上,
∴直线AF与圆D相切
同课章节目录
