浙教版九年级下册 2.3 三角形的内切圆课件(14张)
文档属性
| 名称 | 浙教版九年级下册 2.3 三角形的内切圆课件(14张) |  | |
| 格式 | ppt | ||
| 文件大小 | 691.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 15:45:45 | ||
图片预览



文档简介
2.3 三角形的内切圆
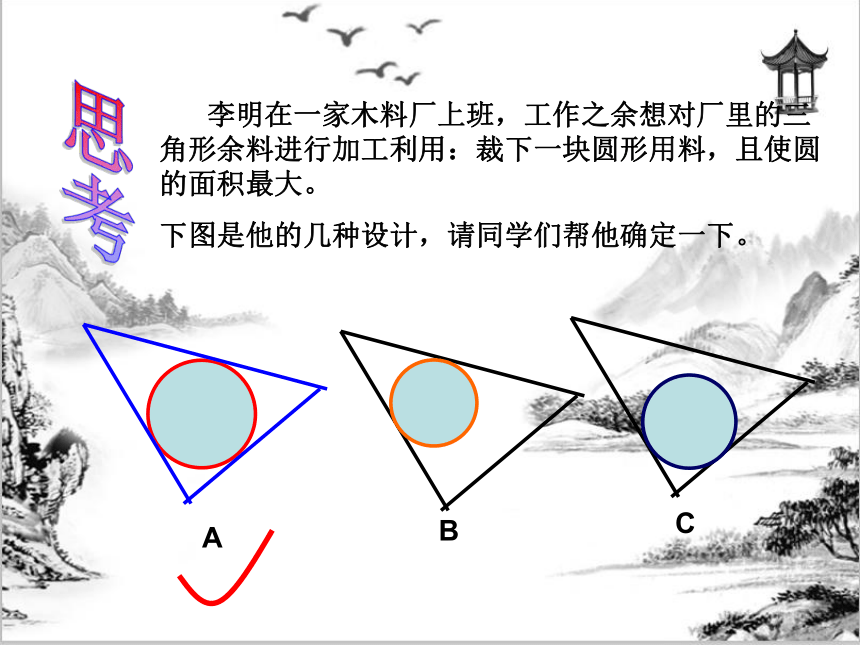
李明在一家木料厂上班,工作之余想对厂里的三角形余料进行加工利用:裁下一块圆形用料,且使圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。
A
B
C
A
B
C
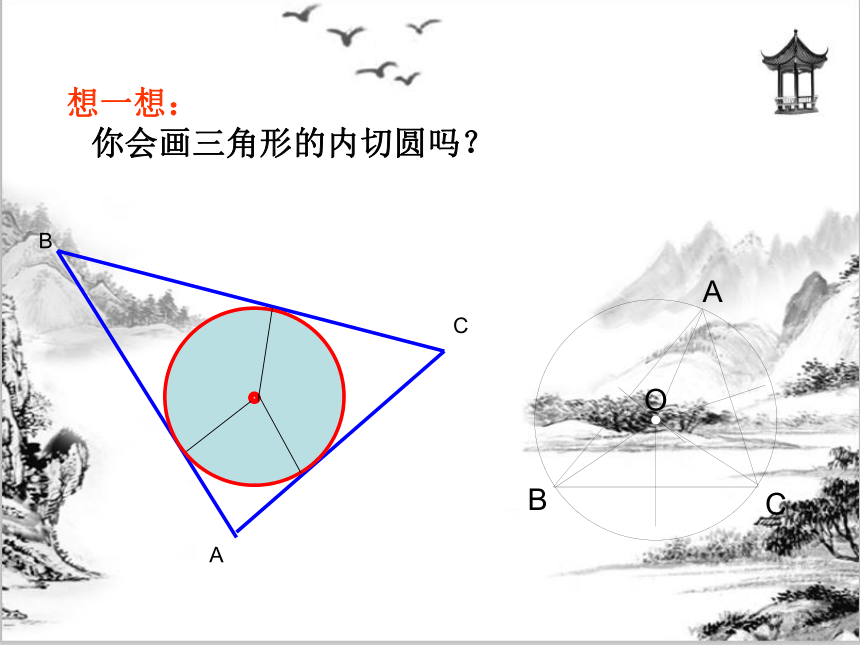
想一想:
你会画三角形的内切圆吗?
2、内心性质:
1、定义:和三角形各边都相切的圆叫做三角
形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形。
内心到三角形三边的距离相等;
内心与顶点连线平分内角。
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
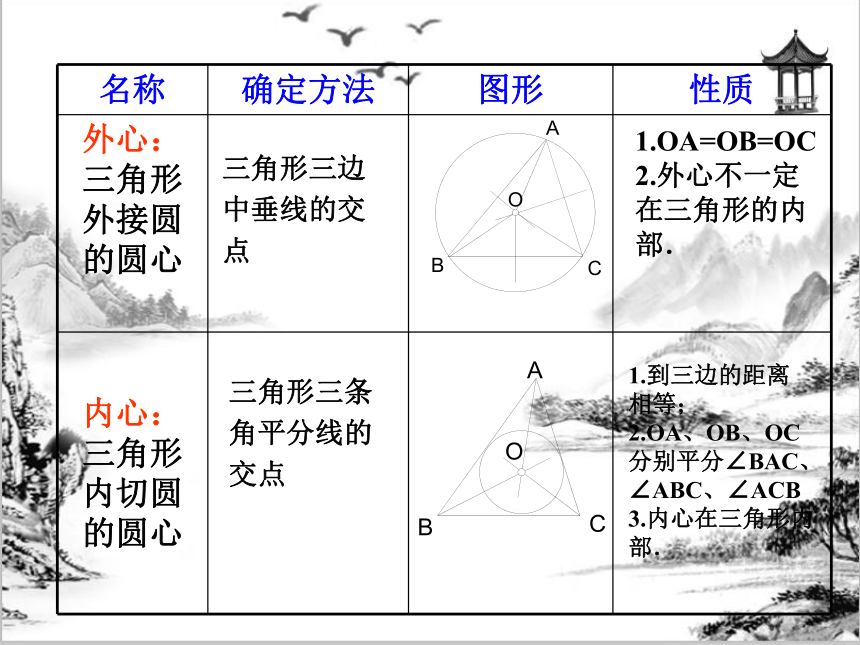
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
中垂线的交
点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
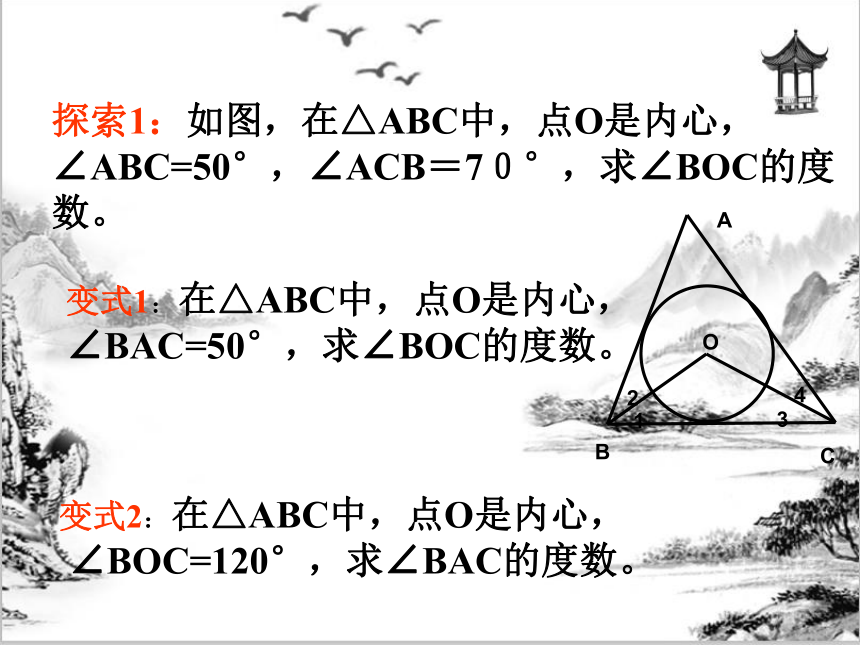
探索1:如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。
O
A
2
4
3
B
C
1
变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。
变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。
探索2:
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。
C
A
B
R
r
O
D
结论:
边长为a的等边三角形的内切圆
半径r= 外接圆半径R= 。
A
B
C
O
a
b
c
D
E
r
如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。
探索3:如图,直角三角形的两直角边分别是a,b,斜边为c 求其内切圆的半径r和外接圆半径R
2cm
r =
a+b-c
2
R=c/2
r
F
探索4:
如图,等腰三角形的两腰长为10,底边为12, 求其内切圆的半径r。
A
B
C
D
E
F
O
结论:
设△ABC的面积为S,周长为L, △ABC内切圆的半径为r,
rL
S
2
1
=
题5:如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC = L
A
B
C
O
D
E
F
1. 三角形内切圆的作法 .
2. 通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,
3. 要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4. 利用三角形内心的性质解题时,要注意整体思想的运
用
已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
A
B
C
F
D
E
x
x
13-x
13-x
9-x
9-x
∴(13-x)+(9-x)=14
略解:设AF=x,则BF=13-x
由切线长定理知:AE=AF=x,BD=BF=13-x,
DC=EC=9-x,又∵BD+CD=14
解得x=4
答:AF=4
BD=9
CE=5
∴AF=4,BD=9,CE=5
补充练习
已知:△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
A
B
C
D
E
补充练习
·
C
B
A
O
I
E
D
2.如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E.
求证:
(1) EI = EB ;
(2)IE ? = AE · DE .
2
)
5
)
3
)
4
)
1
)
李明在一家木料厂上班,工作之余想对厂里的三角形余料进行加工利用:裁下一块圆形用料,且使圆的面积最大。
下图是他的几种设计,请同学们帮他确定一下。
A
B
C
A
B
C
想一想:
你会画三角形的内切圆吗?
2、内心性质:
1、定义:和三角形各边都相切的圆叫做三角
形的内切圆,内切圆的圆心叫做三角形的内心,
这个三角形叫做圆的外切三角形。
内心到三角形三边的距离相等;
内心与顶点连线平分内角。
画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
中垂线的交
点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条
角平分线的
交点
1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
探索1:如图,在△ABC中,点O是内心,∠ABC=50°,∠ACB=70°,求∠BOC的度数。
O
A
2
4
3
B
C
1
变式1:在△ABC中,点O是内心,
∠BAC=50°,求∠BOC的度数。
变式2:在△ABC中,点O是内心,
∠BOC=120°,求∠BAC的度数。
探索2:
求边长为6cm的等边三角形的内切圆半径r与外接圆半径R。
C
A
B
R
r
O
D
结论:
边长为a的等边三角形的内切圆
半径r= 外接圆半径R= 。
A
B
C
O
a
b
c
D
E
r
如:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。
探索3:如图,直角三角形的两直角边分别是a,b,斜边为c 求其内切圆的半径r和外接圆半径R
2cm
r =
a+b-c
2
R=c/2
r
F
探索4:
如图,等腰三角形的两腰长为10,底边为12, 求其内切圆的半径r。
A
B
C
D
E
F
O
结论:
设△ABC的面积为S,周长为L, △ABC内切圆的半径为r,
rL
S
2
1
=
题5:如图,已知⊙O 是△ABC的内切圆,切点分别点D、E、F,设△ABC周长为L。
求证:AE+BC = L
A
B
C
O
D
E
F
1. 三角形内切圆的作法 .
2. 通过类比三角形的外接圆与圆的内接三角形概念得出
三角形的内切圆、圆的外切三角形概念,
3. 要明确“接”和“切”的含义、弄清“内心”与
“外心”的区别,
4. 利用三角形内心的性质解题时,要注意整体思想的运
用
已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
A
B
C
F
D
E
x
x
13-x
13-x
9-x
9-x
∴(13-x)+(9-x)=14
略解:设AF=x,则BF=13-x
由切线长定理知:AE=AF=x,BD=BF=13-x,
DC=EC=9-x,又∵BD+CD=14
解得x=4
答:AF=4
BD=9
CE=5
∴AF=4,BD=9,CE=5
补充练习
已知:△ABC中,E是内心,∠A的平分线和△ABC的外接圆相交于点D,
求证:DE=DB=DC
A
B
C
D
E
补充练习
·
C
B
A
O
I
E
D
2.如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E.
求证:
(1) EI = EB ;
(2)IE ? = AE · DE .
2
)
5
)
3
)
4
)
1
)
