浙教版八年级上册第三章一元一次不等式的性质、运用练习(Word版 无答案)
文档属性
| 名称 | 浙教版八年级上册第三章一元一次不等式的性质、运用练习(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 265.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-16 22:53:53 | ||
图片预览

文档简介
第2讲
一元一次不等式的性质、运用
一、【复习巩固】
1、解不等式(或不等式组):
(1)2(5x+3)≤x-3(1-4x)
(2)
(3)
HYPERLINK
"http://www.czsx.com.cn"
EMBED
Equation.DSMT4
EMBED
Equation.DSMT4
2、练习:1、当
时,不等式>1的解集为<;
2、关于的不等式>的解集是<1,必须满足的条件是
3、不等式2x-1≥3x-5的正整数解为
4、若方程组的解满足x+y<0,求m的取值范围。
5、若方程组的解x、y都是正数,求a的取值范围。
7、一筐橘子分给若干名儿童,如果每人分4个,则剩下9个;如果每人分6个,则最后一名儿童分得的橘子数少于3个,问共有_____名儿童,分了_____个橘子。
二【新知讲解】
1、
一次函数和一元一次不等式的联系:画出函数的图像、观察图象回答下列问题:
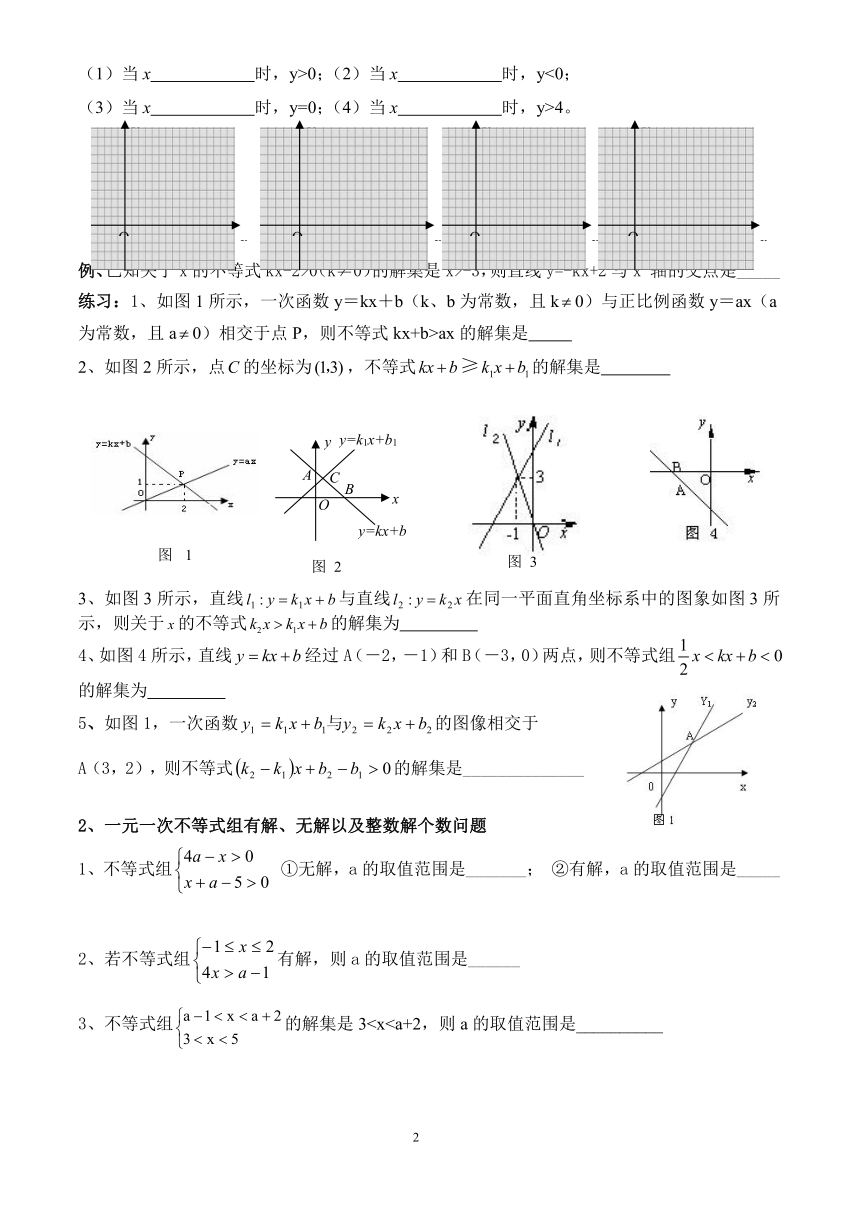
(1)当x
时,y>0;(2)当x
时,y<0;
(3)当x
时,y=0;(4)当x
时,y>4。
例、已知关于x的不等式kx-2>0(k≠0)的解集是x>-3,则直线y=-kx+2与x轴的交点是_____
练习:1、如图1所示,一次函数y=kx+b(k、b为常数,且k0)与正比例函数y=ax(a为常数,且a0)相交于点P,则不等式kx+b>ax的解集是
2、如图2所示,点的坐标为,不等式的解集是
3、如图3所示,直线与直线在同一平面直角坐标系中的图象如图3所示,则关于的不等式的解集为
4、如图4所示,直线经过A(-2,-1)和B(-3,0)两点,则不等式组的解集为
5、如图1,一次函数的图像相交于
A(3,2),则不等式的解集是______________
2、一元一次不等式组有解、无解以及整数解个数问题
1、不等式组
①无解,a的取值范围是_______;
②有解,a的取值范围是_____
2、若不等式组有解,则a的取值范围是______
3、不等式组的解集是34、若关于x的不等式组的整数解共有4个,则m的取值范围是______
变式练习:
(1)
若不等式组
①有解,a的取值范围是_____;②无解,a的取值范围是______
(2)
若关于x的不等式组有解,则a的取值范围是_________
(3)
若不等式组的解集是a-2<x<3,则a的取值范围是_________
(4)
已知关于x的不等式组的整数解共有3个,则a的取值范围是__________
(5)方程组的解满足0<x+y<2,则偶数k的值为_______
(6)若不等式组的整数解共有4个,则a的取值范围是_________
(7)已知不等式组
①若有解,则m______;②若无解,则m______
(8)不等式组的解集是12、
一元一次不等式运用专题问题:重点讲解三种常见的运用问题!
(分配问题)1、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件,若前面每人分4件,则最后一人得到的玩具最多3件,问小朋友的人数至少有多少人?。
2、将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只?
3、
用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
(积分问题)1、某次数学测验共20道题(满分100分)。评分办法是:答对1道给5分,答错1道扣2分,不答不给分。某学生有1道未答。那么他至少答对几道题才能及格?
2、在一次竞赛中有25道题,每道题目答对得4分,不答或答错倒扣2分,如果要求在本次竞赛中的得分不底于60分,至少要答对多少道题目?
3、在比赛中,每名射手打10枪,每命中一次得5分,每脱靶一次扣1分,得到的分数不少于35分的射手为优胜者,要成为优胜者,至少要中靶多少次?
(比较问题)1、某校校长暑假将带领该校“三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,至少要多少名学生选甲旅行社比较好?
2、暑假期间,两名家长计划带领若干名学生去旅游,他们联系了报价为每人500元的两家旅行社,经协商,甲旅行社的优惠条件是:两名家长全额收费,学生都按七折;乙旅行社的优惠条件是:家长,学生都按八折收费。假设这两位家长至带领多少名学生去旅游,他们应该选择甲旅行社?
x
y
O
x
y
O
x
y
O
x
y
O
y
y=k1x+b1
A
C
B
O
x
y=kx+b
图
3
图1
111115
图
2
PAGE
3
一元一次不等式的性质、运用
一、【复习巩固】
1、解不等式(或不等式组):
(1)2(5x+3)≤x-3(1-4x)
(2)
(3)
HYPERLINK
"http://www.czsx.com.cn"
EMBED
Equation.DSMT4
EMBED
Equation.DSMT4
2、练习:1、当
时,不等式>1的解集为<;
2、关于的不等式>的解集是<1,必须满足的条件是
3、不等式2x-1≥3x-5的正整数解为
4、若方程组的解满足x+y<0,求m的取值范围。
5、若方程组的解x、y都是正数,求a的取值范围。
7、一筐橘子分给若干名儿童,如果每人分4个,则剩下9个;如果每人分6个,则最后一名儿童分得的橘子数少于3个,问共有_____名儿童,分了_____个橘子。
二【新知讲解】
1、
一次函数和一元一次不等式的联系:画出函数的图像、观察图象回答下列问题:
(1)当x
时,y>0;(2)当x
时,y<0;
(3)当x
时,y=0;(4)当x
时,y>4。
例、已知关于x的不等式kx-2>0(k≠0)的解集是x>-3,则直线y=-kx+2与x轴的交点是_____
练习:1、如图1所示,一次函数y=kx+b(k、b为常数,且k0)与正比例函数y=ax(a为常数,且a0)相交于点P,则不等式kx+b>ax的解集是
2、如图2所示,点的坐标为,不等式的解集是
3、如图3所示,直线与直线在同一平面直角坐标系中的图象如图3所示,则关于的不等式的解集为
4、如图4所示,直线经过A(-2,-1)和B(-3,0)两点,则不等式组的解集为
5、如图1,一次函数的图像相交于
A(3,2),则不等式的解集是______________
2、一元一次不等式组有解、无解以及整数解个数问题
1、不等式组
①无解,a的取值范围是_______;
②有解,a的取值范围是_____
2、若不等式组有解,则a的取值范围是______
3、不等式组的解集是3
变式练习:
(1)
若不等式组
①有解,a的取值范围是_____;②无解,a的取值范围是______
(2)
若关于x的不等式组有解,则a的取值范围是_________
(3)
若不等式组的解集是a-2<x<3,则a的取值范围是_________
(4)
已知关于x的不等式组的整数解共有3个,则a的取值范围是__________
(5)方程组的解满足0<x+y<2,则偶数k的值为_______
(6)若不等式组的整数解共有4个,则a的取值范围是_________
(7)已知不等式组
①若有解,则m______;②若无解,则m______
(8)不等式组的解集是1
一元一次不等式运用专题问题:重点讲解三种常见的运用问题!
(分配问题)1、一堆玩具分给若干个小朋友,若每人分3件,则剩余4件,若前面每人分4件,则最后一人得到的玩具最多3件,问小朋友的人数至少有多少人?。
2、将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只?
3、
用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空。请问:有多少辆汽车?
(积分问题)1、某次数学测验共20道题(满分100分)。评分办法是:答对1道给5分,答错1道扣2分,不答不给分。某学生有1道未答。那么他至少答对几道题才能及格?
2、在一次竞赛中有25道题,每道题目答对得4分,不答或答错倒扣2分,如果要求在本次竞赛中的得分不底于60分,至少要答对多少道题目?
3、在比赛中,每名射手打10枪,每命中一次得5分,每脱靶一次扣1分,得到的分数不少于35分的射手为优胜者,要成为优胜者,至少要中靶多少次?
(比较问题)1、某校校长暑假将带领该校“三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,至少要多少名学生选甲旅行社比较好?
2、暑假期间,两名家长计划带领若干名学生去旅游,他们联系了报价为每人500元的两家旅行社,经协商,甲旅行社的优惠条件是:两名家长全额收费,学生都按七折;乙旅行社的优惠条件是:家长,学生都按八折收费。假设这两位家长至带领多少名学生去旅游,他们应该选择甲旅行社?
x
y
O
x
y
O
x
y
O
x
y
O
y
y=k1x+b1
A
C
B
O
x
y=kx+b
图
3
图1
111115
图
2
PAGE
3
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
