2020-2021学年浙教版八年级上册 第5章 一次函数 专题培优(Word版 附答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级上册 第5章 一次函数 专题培优(Word版 附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1010.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 23:43:02 | ||
图片预览


文档简介
2020-2021学年浙教版八年级上册函数与一次函数专题培优
姓名
班级
学号
基础巩固
1.对于圆的周长公式C
=
2πR,下列说法正确的是( ).
A.π,R是变量,2是常量
B.R是变量,C是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
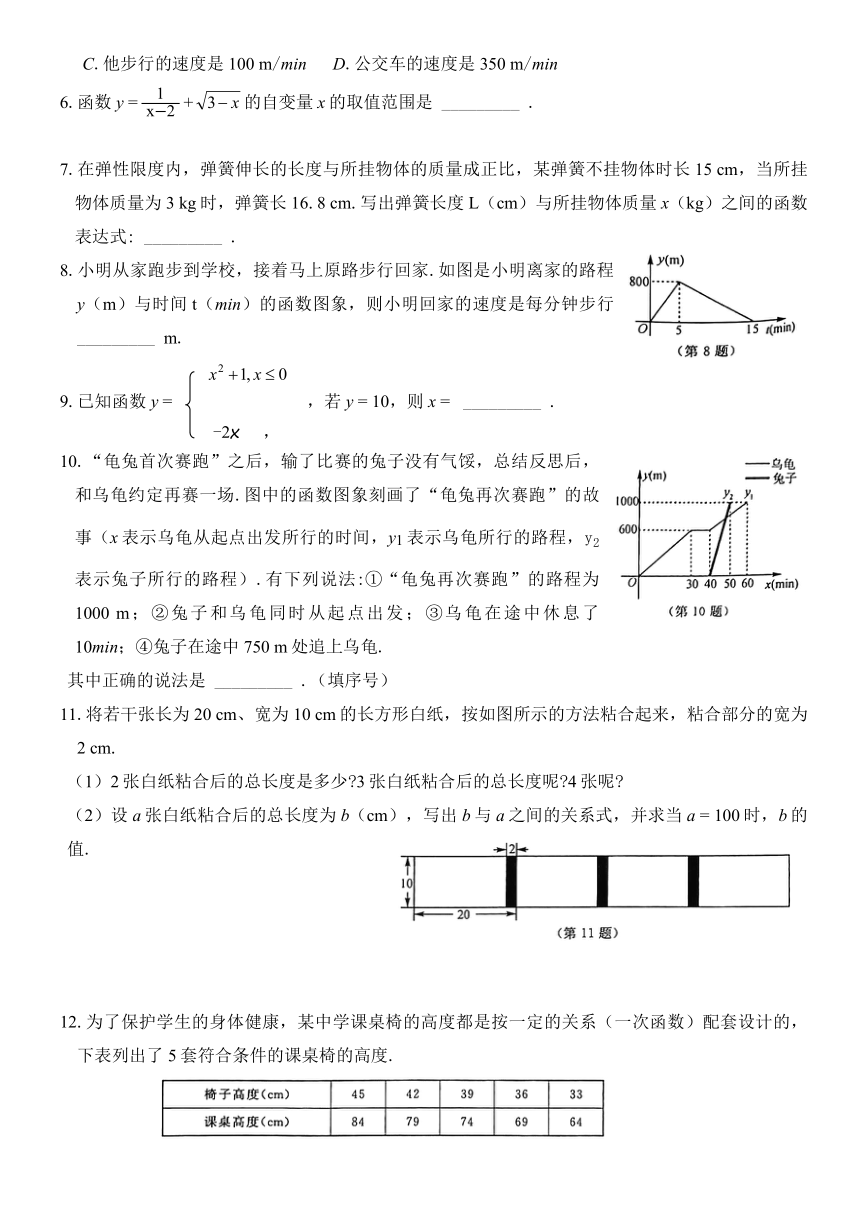
2.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.根据如图,在下列选项中指出白昼时长低于11h的节气( ).
A.惊蛰
B.小满
C.立秋
D.大寒
3.下列图象中,表示y是x的函数的个数有( ).
A.1个
B.2个
C.3个
D.4个
4.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校的行驶路程s(单位:m)与时间t(单位:min)之间的函数关系的大致图象是( ).
5.小亮从家步行到公交车站台,等公交车去学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系.下列说法错误的是( ).
A.他离家8
km共用了30min
B.他等公交车时间为6min
C.他步行的速度是100
m/min
D.公交车的速度是350
m/min
6.函数y
=
+的自变量x的取值范围是
_________
.
7.在弹性限度内,弹簧伸长的长度与所挂物体的质量成正比,某弹簧不挂物体时长15
cm,当所挂物体质量为3
kg时,弹簧长16.8
cm.写出弹簧长度L(cm)与所挂物体质量x(kg)之间的函数表达式:
_________
.
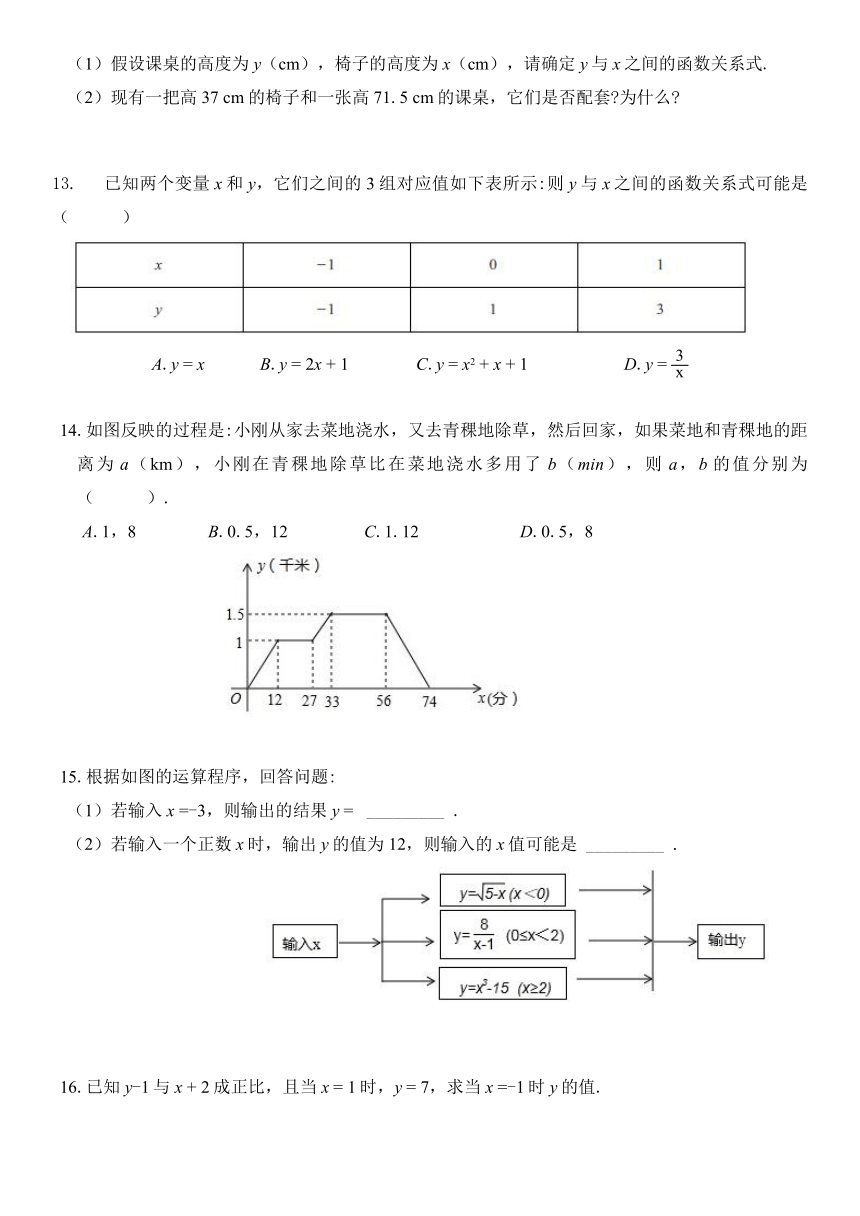
8.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(m)与时间t(min)的函数图象,则小明回家的速度是每分钟步行
_________
m.
9.已知函数y
=
,若y
=
10,则x
=
_________
.
10.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000
m;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10min;④兔子在途中750
m处追上乌龟.
其中正确的说法是
_________
.(填序号)
11.将若干张长为20
cm、宽为10
cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为2
cm.
(1)2张白纸粘合后的总长度是多少?3张白纸粘合后的总长度呢?4张呢?
(2)设a张白纸粘合后的总长度为b(cm),写出b与a之间的关系式,并求当a
=
100时,b的值.
12.为了保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出了5套符合条件的课桌椅的高度.
(1)假设课桌的高度为y(cm),椅子的高度为x(cm),请确定y与x之间的函数关系式.
(2)现有一把高37
cm的椅子和一张高71.5
cm的课桌,它们是否配套?为什么?
已知两个变量x和y,它们之间的3组对应值如下表所示:则y与x之间的函数关系式可能是( )
A.y
=
x
B.y
=
2x
+
1
C.y
=
x2
+
x
+
1
D.y
=
14.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a(km),小刚在青稞地除草比在菜地浇水多用了b(min),则a,b的值分别为( ).
A.1,8
B.0.5,12
C.1.12
D.0.5,8
15.根据如图的运算程序,回答问题:
(1)若输入x
=-3,则输出的结果y
=
_________
.
(2)若输入一个正数x时,输出y的值为12,则输入的x值可能是
_________
.
16.已知y-1与x
+
2成正比,且当x
=
1时,y
=
7,求当x
=-1时y的值.
17.某机动车出发前邮箱内有油42
L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.根据图象回答问题:(1)机动车行驶5h后加油,途中加油
_________
L.
(2)机动车在加油前的行驶中每小时耗油多少升?
(3)如果加油站距目的地还有400
km,车速为60
km/h,要到达目的地,油箱中的油是否够用?请说明理由.
18.阅读下面材料,再回答问题:
一般地,如果两数y
=
f(x)对于自变量取值范围内的任意x,都有f(-x)
=-
f(x),那么y
=
f(x)就叫做奇函数;如果函数y
=
f(x)对于自变量取值范围内的任意x,都有f(-x)
=
f(x),那么y
=
f(x)就叫做偶函数.
例如:f(x)
=
x3
+
x,当x取任意实数时,f(-x)
=
(-x)3
+
(-x)
=-(x3
+
x),
即f(-
x)
=-f(x),∴f(x)
=
x3
+
x为奇函数.
又如f(x)
=
|x|,当x取任意实数时,f(-
x)
=
|
-x|
=
|x|
=
f(x),
即f(-
x)
=
f(x),∴f(x)
=
|x|是偶函数.
问题(1):下列函数中:①y
=
x4;②y
=
x2
+
1;③y
=
;④y
=;⑤y
=
x
+
.
所有奇函数是
_________
,所有偶函数是
_________
.(填序号)
问题(2):请你再分别写出一个奇函数和一个偶函数.
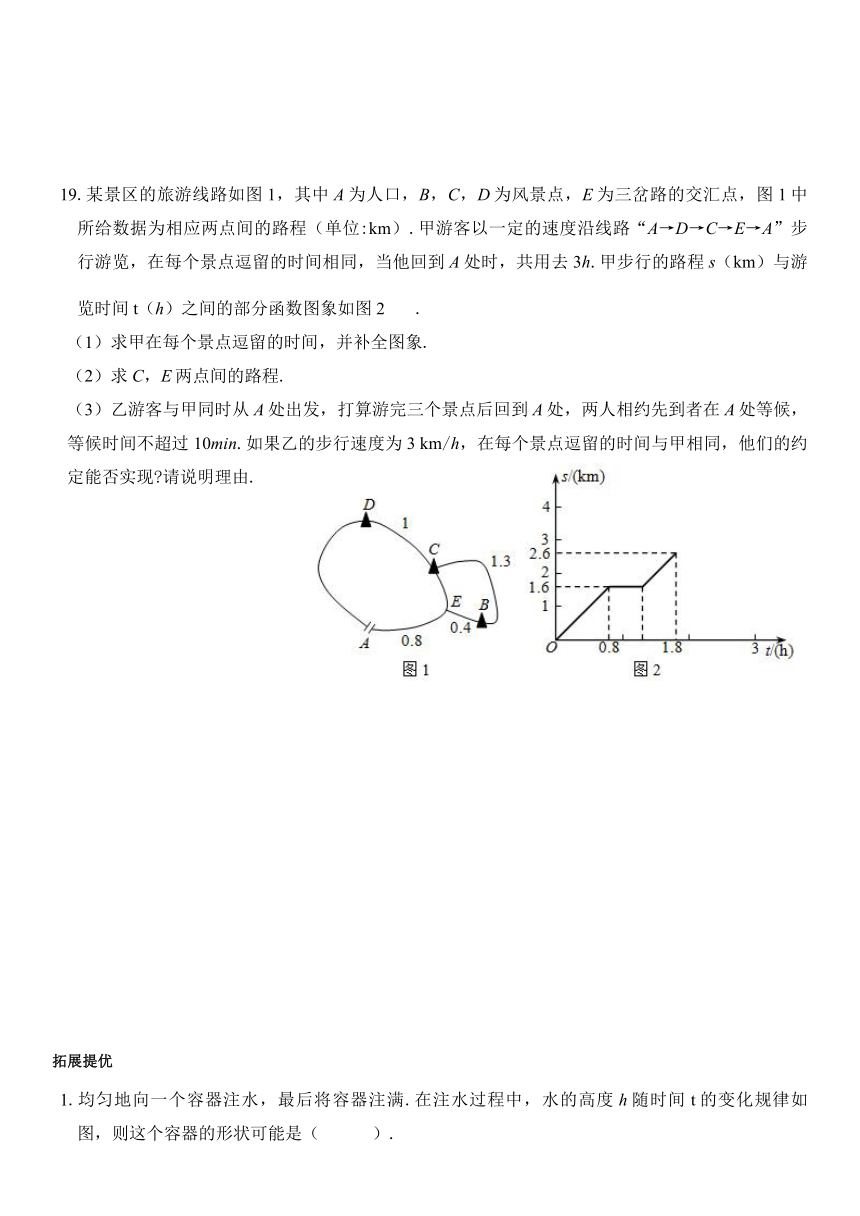
19.某景区的旅游线路如图1,其中A为人口,B,C,D为风景点,E为三岔路的交汇点,图1中所给数据为相应两点间的路程(单位:km).甲游客以一定的速度沿线路“A→D→C→E→A”步行游览,在每个景点逗留的时间相同,当他回到A处时,共用去3h.甲步行的路程s(km)与游览时间t(h)之间的部分函数图象如图2.
(1)求甲在每个景点逗留的时间,并补全图象.
(2)求C,E两点间的路程.
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候,等候时间不超过10min.如果乙的步行速度为3
km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.
拓展提优
1.均匀地向一个容器注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图,则这个容器的形状可能是( ).
2.根据如图的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于( ).
A.9
B.7
C.-
9
D.-7
第2题
第4题
3.若规定[x]表示不大于x的最大整数,例如[2.3]
=
2,则函数y
=
x-[x]的图象为( ).
4.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB的面积为y,如果y与x之间的函数图象如图2,那么长方形ABCD的面积为
_________
.
5.实验室里有一个水平放置的长方体容器,从内部量得它的高是15
cm,底面的长是30
cm,宽是20
cm,容器内的水深为x(cm).现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点A的三条棱的长分别为10
cm,10
cm,y(cm)(y≤15),当铁块的顶部高出水面2
cm时,x,y满足的关系式为
_________
.
6.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t
=
0.7s时,h的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需要多少时间?
7.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x
>
200时,y与x的函数表达式.
(2)小明家5月份缴纳电费117元,请问:小明家这个月用电多少度?
冲刺重高
1.如图1,点G是BC的中点,点H在AF上,动点P以每秒2
cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB
=
6
cm,则下列四个结论中:①图1中的BC长是8
cm;②图2中的点M表示第4秒时y的值为24;③图1中的CD长是4
cm;④图1中的DE长是3
cm;⑤图2中的点Q表示第8秒时y的值为33;⑥图2中的点N表示第12秒时y的值为18
cm2.正确的个数有( ).
A.3个
B.4个
C.5个
D.6个
第1题
第2题
2.如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d
=
5-x(0≤x≤5),给出以下四个结论:①AF
=
2;②BF
=
5;③OA
=
5;④OB
=
3.其中正确结论的序号是
_________
.
3.函数y
=
|x-1|
+
2|x-2|
+
3|x-3|
+
4|x-4|的最小值是
_________
.
4.如果记
=
f(x),并且f(1)表示当x
=
1时,y的值,即f(1)
=
=
,同理f()表示出:x
=
时,那么f()
=
=
,………那么f(1)
+
f(2)
+
f()
+
f(3)+
f()
+
…
+
f(n)
+
f()
=
_________
.(结果用含有n的代数式表示,n为正整数)
5.如图1,在长方形ABCD中,AB
=
30
cm,BC
=
60
cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A匀速运动、到达点A后停止.若点P,Q同时出发,在运动过程中,点Q停留了1s,图2是P,Q两点在折线AB→BC→CD上相距的路程s(cm)与时间t(s)之间的函数关系图象.
(1)请解释图中点H的实际意义.
(2)求P,Q两点的运动速度.
(3)将图2补充完整.
(4)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值.
姓名
班级
学号
基础巩固
1.对于圆的周长公式C
=
2πR,下列说法正确的是( ).
A.π,R是变量,2是常量
B.R是变量,C是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
2.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.根据如图,在下列选项中指出白昼时长低于11h的节气( ).
A.惊蛰
B.小满
C.立秋
D.大寒
3.下列图象中,表示y是x的函数的个数有( ).
A.1个
B.2个
C.3个
D.4个
4.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校的行驶路程s(单位:m)与时间t(单位:min)之间的函数关系的大致图象是( ).
5.小亮从家步行到公交车站台,等公交车去学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系.下列说法错误的是( ).
A.他离家8
km共用了30min
B.他等公交车时间为6min
C.他步行的速度是100
m/min
D.公交车的速度是350
m/min
6.函数y
=
+的自变量x的取值范围是
_________
.
7.在弹性限度内,弹簧伸长的长度与所挂物体的质量成正比,某弹簧不挂物体时长15
cm,当所挂物体质量为3
kg时,弹簧长16.8
cm.写出弹簧长度L(cm)与所挂物体质量x(kg)之间的函数表达式:
_________
.
8.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(m)与时间t(min)的函数图象,则小明回家的速度是每分钟步行
_________
m.
9.已知函数y
=
,若y
=
10,则x
=
_________
.
10.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000
m;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10min;④兔子在途中750
m处追上乌龟.
其中正确的说法是
_________
.(填序号)
11.将若干张长为20
cm、宽为10
cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为2
cm.
(1)2张白纸粘合后的总长度是多少?3张白纸粘合后的总长度呢?4张呢?
(2)设a张白纸粘合后的总长度为b(cm),写出b与a之间的关系式,并求当a
=
100时,b的值.
12.为了保护学生的身体健康,某中学课桌椅的高度都是按一定的关系(一次函数)配套设计的,下表列出了5套符合条件的课桌椅的高度.
(1)假设课桌的高度为y(cm),椅子的高度为x(cm),请确定y与x之间的函数关系式.
(2)现有一把高37
cm的椅子和一张高71.5
cm的课桌,它们是否配套?为什么?
已知两个变量x和y,它们之间的3组对应值如下表所示:则y与x之间的函数关系式可能是( )
A.y
=
x
B.y
=
2x
+
1
C.y
=
x2
+
x
+
1
D.y
=
14.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a(km),小刚在青稞地除草比在菜地浇水多用了b(min),则a,b的值分别为( ).
A.1,8
B.0.5,12
C.1.12
D.0.5,8
15.根据如图的运算程序,回答问题:
(1)若输入x
=-3,则输出的结果y
=
_________
.
(2)若输入一个正数x时,输出y的值为12,则输入的x值可能是
_________
.
16.已知y-1与x
+
2成正比,且当x
=
1时,y
=
7,求当x
=-1时y的值.
17.某机动车出发前邮箱内有油42
L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示.根据图象回答问题:(1)机动车行驶5h后加油,途中加油
_________
L.
(2)机动车在加油前的行驶中每小时耗油多少升?
(3)如果加油站距目的地还有400
km,车速为60
km/h,要到达目的地,油箱中的油是否够用?请说明理由.
18.阅读下面材料,再回答问题:
一般地,如果两数y
=
f(x)对于自变量取值范围内的任意x,都有f(-x)
=-
f(x),那么y
=
f(x)就叫做奇函数;如果函数y
=
f(x)对于自变量取值范围内的任意x,都有f(-x)
=
f(x),那么y
=
f(x)就叫做偶函数.
例如:f(x)
=
x3
+
x,当x取任意实数时,f(-x)
=
(-x)3
+
(-x)
=-(x3
+
x),
即f(-
x)
=-f(x),∴f(x)
=
x3
+
x为奇函数.
又如f(x)
=
|x|,当x取任意实数时,f(-
x)
=
|
-x|
=
|x|
=
f(x),
即f(-
x)
=
f(x),∴f(x)
=
|x|是偶函数.
问题(1):下列函数中:①y
=
x4;②y
=
x2
+
1;③y
=
;④y
=;⑤y
=
x
+
.
所有奇函数是
_________
,所有偶函数是
_________
.(填序号)
问题(2):请你再分别写出一个奇函数和一个偶函数.
19.某景区的旅游线路如图1,其中A为人口,B,C,D为风景点,E为三岔路的交汇点,图1中所给数据为相应两点间的路程(单位:km).甲游客以一定的速度沿线路“A→D→C→E→A”步行游览,在每个景点逗留的时间相同,当他回到A处时,共用去3h.甲步行的路程s(km)与游览时间t(h)之间的部分函数图象如图2.
(1)求甲在每个景点逗留的时间,并补全图象.
(2)求C,E两点间的路程.
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候,等候时间不超过10min.如果乙的步行速度为3
km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.
拓展提优
1.均匀地向一个容器注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图,则这个容器的形状可能是( ).
2.根据如图的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于( ).
A.9
B.7
C.-
9
D.-7
第2题
第4题
3.若规定[x]表示不大于x的最大整数,例如[2.3]
=
2,则函数y
=
x-[x]的图象为( ).
4.如图1,在长方形ABCD中,动点P从点A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PAB的面积为y,如果y与x之间的函数图象如图2,那么长方形ABCD的面积为
_________
.
5.实验室里有一个水平放置的长方体容器,从内部量得它的高是15
cm,底面的长是30
cm,宽是20
cm,容器内的水深为x(cm).现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点A的三条棱的长分别为10
cm,10
cm,y(cm)(y≤15),当铁块的顶部高出水面2
cm时,x,y满足的关系式为
_________
.
6.小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t
=
0.7s时,h的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需要多少时间?
7.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x
>
200时,y与x的函数表达式.
(2)小明家5月份缴纳电费117元,请问:小明家这个月用电多少度?
冲刺重高
1.如图1,点G是BC的中点,点H在AF上,动点P以每秒2
cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB
=
6
cm,则下列四个结论中:①图1中的BC长是8
cm;②图2中的点M表示第4秒时y的值为24;③图1中的CD长是4
cm;④图1中的DE长是3
cm;⑤图2中的点Q表示第8秒时y的值为33;⑥图2中的点N表示第12秒时y的值为18
cm2.正确的个数有( ).
A.3个
B.4个
C.5个
D.6个
第1题
第2题
2.如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d
=
5-x(0≤x≤5),给出以下四个结论:①AF
=
2;②BF
=
5;③OA
=
5;④OB
=
3.其中正确结论的序号是
_________
.
3.函数y
=
|x-1|
+
2|x-2|
+
3|x-3|
+
4|x-4|的最小值是
_________
.
4.如果记
=
f(x),并且f(1)表示当x
=
1时,y的值,即f(1)
=
=
,同理f()表示出:x
=
时,那么f()
=
=
,………那么f(1)
+
f(2)
+
f()
+
f(3)+
f()
+
…
+
f(n)
+
f()
=
_________
.(结果用含有n的代数式表示,n为正整数)
5.如图1,在长方形ABCD中,AB
=
30
cm,BC
=
60
cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A匀速运动、到达点A后停止.若点P,Q同时出发,在运动过程中,点Q停留了1s,图2是P,Q两点在折线AB→BC→CD上相距的路程s(cm)与时间t(s)之间的函数关系图象.
(1)请解释图中点H的实际意义.
(2)求P,Q两点的运动速度.
(3)将图2补充完整.
(4)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
