2020年秋浙教版八年级数学上册第4章 图形与坐标单元培优测试卷(word版 含解析)
文档属性
| 名称 | 2020年秋浙教版八年级数学上册第4章 图形与坐标单元培优测试卷(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-17 11:17:48 | ||
图片预览



文档简介
2020年秋浙教版八年级数学上册第4章
图形与坐标单元培优测试卷含解析
一、选择题(共10题;共30分)
1.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是(??
).
A.?小李现在位置为第1排第2列?????????????????????????B.?小张现在位置为第3排第2列
C.?小王现在位置为第2排第2列?????????????????????????D.?小谢现在位置为第4排第2列
2.某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(-2,-3),儿童公园所在位置的坐标为(-4,-2),则(0,4)所在的位置是(???
)
A.?医院?????????????????????????B.?学校???????????????????????C.?汽车站????????????????????D.?水果店
3.如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,C,D的位置时,其中表示错误的是(???
)
A.?A(4,30°)????????????B.?B(2,90°)????????C.?C(6,120°)??????????????D.?D(3,240°)
4.点P在第四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为(??
)
A.?(-3,-2)????????????????B.?(3,-2)????????????????C.?(2,3)???????????????D.?(2,-3)
5.在平面直角坐标系中,将点
向右平移4个单位长度,得到的对应点
的坐标为(???
)
A.??????????????????????????B.????????????????????C.???????????????????D.?
6.在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是(??
)
A.?(1,?1),(?1,?3)????????B.?(1,1),(3,3)???????????C.?(?1,3),(3,1)????????????D.?(3,2),(1,4)
7.已知三角形的三个顶点坐标分别为(-2,1),(2,3),(-3,-1),把这个三角形运动到一个确定位置,在下列各点的坐标中,是经过平移得到的是(?
??)
A.?(0,3),(0,1),(-1,-1)??????????B.?(-3,2),(3,2),(-4,0)
C.?(1,-2),(3,2),(-1,-3)????????D.?(-1,3),(3,5),(-2,1)
8.如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A.?(1,3)??????????????B.?(5,3)?????????????????C.?(6,1)????????????????D.?(8,2)
9.已知点
在第二象限,则m的取值范围在数轴上表示正确的是(?
)
A.????B.?????C.?????D.?
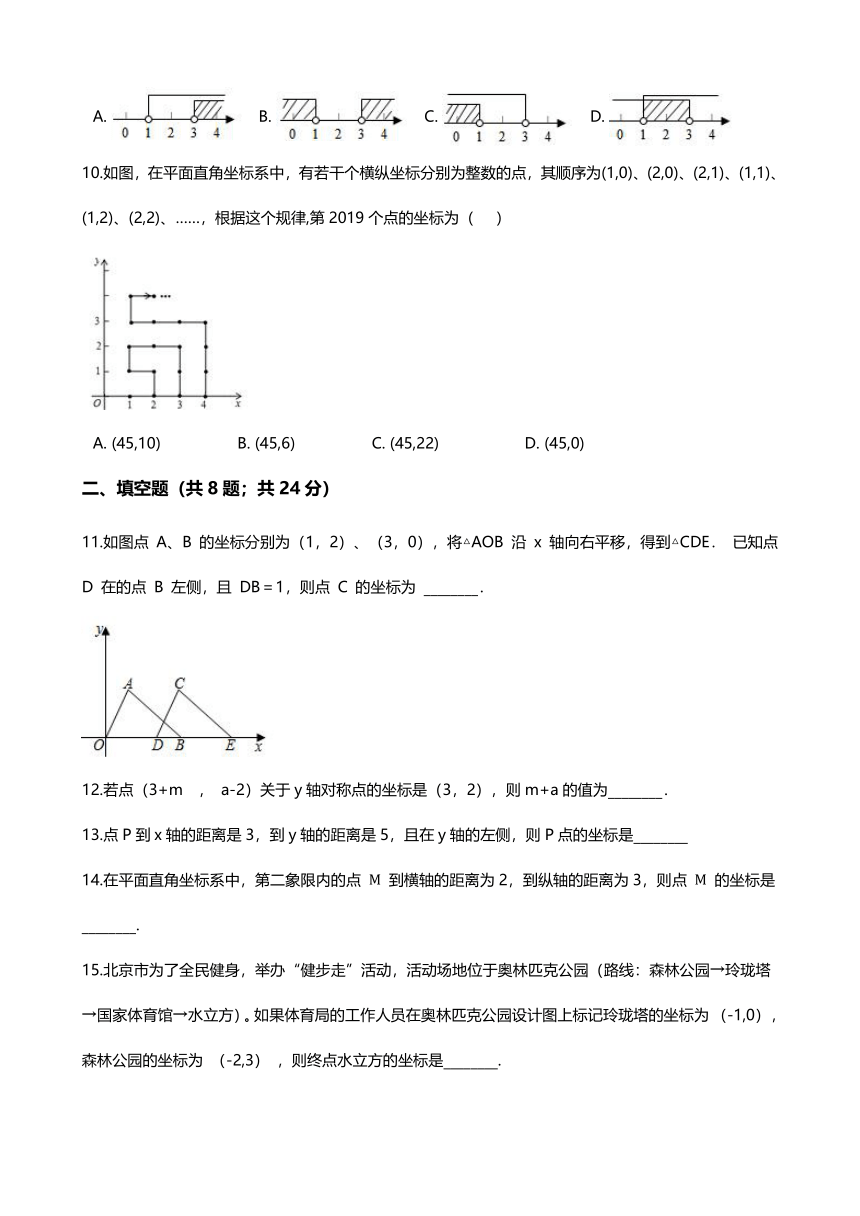
10.如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、……,根据这个规律,第2019个点的坐标为(???
)
A.?(45,10)?????????????????B.?(45,6)?????????????????C.?(45,22)???????????????????D.?(45,0)
二、填空题(共8题;共24分)
11.如图点
A、B
的坐标分别为(1,2)、(3,0),将△AOB
沿
x
轴向右平移,得到△CDE.
已知点
D
在的点
B
左侧,且
DB=1,则点
C
的坐标为
________.
12.若点(3+m
,
a-2)关于y轴对称点的坐标是(3,2),则m+a的值为________.
13.点P到x轴的距离是3,到y轴的距离是5,且在y轴的左侧,则P点的坐标是________
14.在平面直角坐标系中,第二象限内的点
到横轴的距离为2,到纵轴的距离为3,则点
的坐标是________.
15.北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育馆→水立方)。如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为
(-1,0)
,森林公园的坐标为
(-2,3)
,则终点水立方的坐标是________.
16.若点P(-1,a)与Q(b,2)关于x轴对称,则a+b=________.
17.在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点A(1,-2),经过一个变换后对应点为A1
,
经过2个变换后对应点为A2
,
…经过n个变换后对应点为An
,
则用含n的代数式表示点An的坐标为________。
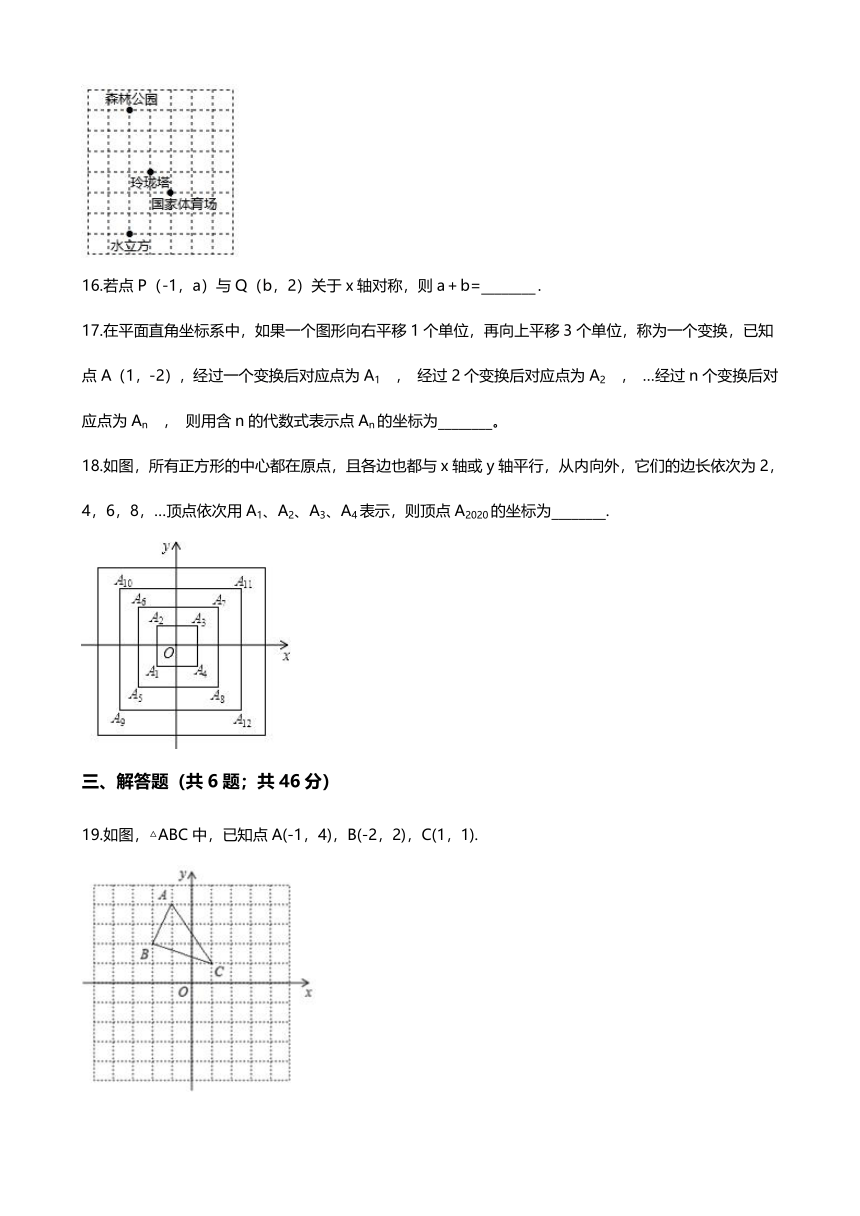
18.如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为________.
三、解答题(共6题;共46分)
19.如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).
(1)作ΔABC关于x轴对称的△A1B1C1
,
并写出点A1
,
B1
,
C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2
,
并写出点A2
,
B2
,
C2的坐标,
(3)观察点A1
,
B1
,
C1和A2
,
B2
,
C2的坐标,请用文字语言归纳点A1和A2
,
B1和B2
,
C1和C2坐标之间的关系.
20.如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:
(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
21.在平面直角坐标系中.
(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4)若AB∥x
轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段
AB
的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
22.如图,在平面直角坐标系中,已知点
,
,
三点.
(1)求
的面积;
(2)如果在第二象限内有一点
,且四边形ABOP的面积是
的面积的两倍;求满足条件的P点坐标.
23.已知点P
(2a﹣10,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值:
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
24.如图1,在平面直角坐标系中,A、B在坐标轴上,其中A(0,a),B(b
,
0)满足|a-3|+
=0.
(1)求A、B两点的坐标;
(2)将AB平移到CD
,
A点对应点C(-2,m),CD交y轴于E
,
若△ABC的面积等于13,求点E的坐标;
(3)如图2,若将AB平移到CD
,
点C、D也在坐标轴上,F为线段AB上一动点,(不包括点A
,
点B),连接OF、FP平分∠BFO
,
∠BCP=2∠PCD
,
试探究∠COF
,
∠OFP
,
∠CPF的数量关系.
答案
一、选择题
1.解:A.
小李现在位置为第1排第4列,故A选项错误;
B.
小张现在位置为第3排第2列,故B选项正确;
C.
小王现在位置为第2排第3列,故C选项错误;
D.
小谢现在位置为第4排第4列,故D选项错误.
故答案为:B.
2.解:根据题意,建立平面直角坐标系如图:
(0,4)所在的位置是学校.
故答案为:B.
3.由题意可知A、B、C、D的坐标可表示为:
A(4,30°),故A不符合题意;
B(2,90°),故B不符合题意;
C(6,120°),故C不符合题意;
D(4,240°),故D符合题意,
故答案为:D.
4.解:∵点P在第四象限,
∴横坐标为3,纵坐标为-2.
故答案为:A
5.解:点A(-2,3)向右平移4个单位长度后得到的对应点A′的坐标为(-2+4,3),
即(2,3),
故答案为:C.
6.解:根据题意可得:将线段AB平移后,A,B的对应点的坐标与原A.
B点的坐标差必须相等.
A.
A点横坐标差为0,纵坐标差为1,B点横坐标差为4,纵坐标差为5,A.
B点对应点的坐标差不相等,故不合题意;
B.
A点横坐标差为0,纵坐标差为?1,B点横坐标差为0,纵坐标差为?1,A.
B点对应点的坐标差相等,故合题意;
C.
A点横坐标差为2,纵坐标差为?3,B点的横坐标差为0,纵坐标差为1,A.
B点对应点的坐标差不相等,故不合题意;
D.
,A点横坐标差为?2,纵坐标差为?2,B点横坐标差为2,纵坐标差为?2,A.
B点对应点的坐标差不相等,故不合题意;
故答案为:B
7.A.由(﹣2,1)到(0,3)是向右平移了2个单位,向上平移了2个单位;而由(2,3)到(0,1)是向左平移了2个单位,向下平移了2个单位,故不符合题意;
B.
由(﹣2,1)到(﹣3,2)是向左平移了1个单位,向上平移了1个单位;而由(2,3)到(3,2)是向右平移了1个单位,向下平移了1个单位,故不符合题意;
C.
由(﹣2,1)到(1,﹣2)是向右平移了3个单位,向下平移了3个单位;而由(2,3)到(3,2)是向右平移了1个单位,向下平移了1个单位,故不符合题意;
D.
由(﹣2,1),(2,3),(﹣3,﹣1)到(﹣1,3),(3,5),(﹣2,1)都是向右平移了1个单位,向上平移了2个单位,故符合题意;
故答案为:D.
8.解:如图所示:“马”位于(6,1).
故答案为:C
.
9.解:∵
点
在第二象限
∴
解之:m>3,m>1
∴m的取值范围是m>3.
故答案为:A.
10.解:将其左侧相连,看作正方形边上的点,如图所示.
边长为0的正方形,有1个点;边长为1的正方形,有3个点;边长为2的正方形,有5个点;…,
∴边长为n的正方形有2n+1个点,
∴边长为n的正方形边上与内部共有1+3+5+…+2n+1=(n+1)2个点.
∵2019=45×45-6,
结合图形即可得知第2019个点的坐标为(45,6).
故答案为:B.
二、填空题
11.解:
的坐标为
,
,
,
,
向右平移了2个单位长度,
点A的坐标为
,
点C的坐标为:
.
故答案是:
.
12.解:∵点(
,
)关于y轴对称点的坐标是(3,2),
∴
,
,
解得:
,
,
∴
,
故答案为:-2.
13.解:∵点P到x轴的距离是3,∴点P的纵坐标是
,
∵点P到y轴的距离是5,且在y轴左侧,∴点P的横坐标是
∴点P的坐标是
或
.
故答案是:
或
.
14.∵点
到横轴的距离为2,到纵轴的距离为3,
∴|y|=2,|x|=3,
由M是第二象限的点,得:
x=?3,y=2.
即点M的坐标是(?3,2),
故答案为:(?3,2).
15.解:根据玲珑塔的坐标可知,原点的坐标位置
∴水立方的坐标为(-2,-3)
16.解:∵点P(-1,a)与Q(b,2)关于x轴对称,
∴b=-1,a=-2
∴a+b=-1-2=-3
故答案为:-3
17.由题意可知:
横坐标每次向右平移一个单位,横坐标依次增加1,2,3……n;
纵坐标每次向上平移三个单位,纵坐标依次增加3,6,9……3n;
即An的坐标表达式为(1+n,
-2+3n)
18.解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4
,
(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数).
∵2020=505×4,
∴A2020(505,﹣505).
故答案为:(505,﹣505).
三、解答题
19.(1)解:如下图所示:
∵A(-1,4),B(-2,2),C(1,1)
A1
,
B1
,
C1和A,B,C关于x轴对称
∴A1(-1,-4),B1(-2,-2),C1(1,-1)
(2)解:如下图所示:
∵A(-1,4),B(-2,2),C(1,1)
A2
,
B2
,
C2和A,B,C关于y轴对称
∴A2(1,4),B2(2,2),C2(-1,1)
(3)解:根据(1)(2)中得出的坐标可知,A1和A2
,
B1和B2
,
C1和C2坐标之间的关系为:横坐标互为相反数,纵坐标也互为相反数.
20.
(1)解:以O点为原点,水平向右为正方向画x轴,垂直往上为正方向画y轴,依此建立直角坐标系即可
(2)解:根据(1)建立的直角坐标系,D(1,2),E(4,3),F(0,4)
(3)解:在(1)建立的直角坐标系标记出点M(6,2)、N(4,4)的位置.
21.
(1)解:根据题意知,2a﹣6=0,解得:a=3,
∴点
P
的坐标为(0,7)
(2)解:∵AB∥x
轴,
∴m﹣1=4,解得
m=5,∵点
B
在第一象限,
∴n+1>0,解得
n>﹣1
(3)解:由(2)知点
A(﹣3,4),
∵AB=6,且点
B
在第一象限,
∴点
B(3,4),
由点
P(0,7)可得
PA2=(﹣3﹣0)2+(4﹣7)2=18、PB2=(3﹣0)2+(4﹣7)2=18,
∵AB2=36,
∴PA2+PB2=AB2
,
且PA=PB,
因此,△PAB是等腰直角三角形。
22.
(1)解:
,
,
,
;
(2)解:
,
,
,
,
,
又
,
,
解得:
,
.
23.
(1)∵点P
(2a﹣10,1﹣a)位于第三象限,
∴1﹣a=﹣3,
∴a=4;
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,
又点Q(x,y)位于第二象限,
所以y>0;
取y=1,得点Q的坐标为(﹣4,1);
(3)∵点P
(2a﹣10,1﹣a)位于第三象限,
∴
,
∴1<a<5,
∵点P的横、纵坐标都是整数,
∴a=2或3或4;
当a=2时,点P(﹣6,﹣1),则PQ>1,
当a=3时,点P(﹣4,﹣2),则PQ>2,
当a=4时,点P(﹣2,﹣3),则PQ>3.
24.
(1)由题意得,a-3=0,b-4=0,
解得,a=3,b=4,
则A(0,3),B(4,0);
(2)如图1所示,
∵DABC的面积等于13,根据A,B,C三点的坐标,
可得:
,(m<0)
解得,m=-2,
则点C的坐标为(-2,-2),
根据平移规律,则有点D的坐标为(2,-5),
设直线CD的解析式为:y=cx+d,
,解得
,
∴CD的解析式为:
,
∴CD与y轴的交点E的坐标为(0,
);
(3)如图2所示,作HP∥AB交AD于H,OG∥AB交FP于G,
设∠OFP=x,∠PCD=y,
则∠BFP=x,∠PCB=2y,
∵HP∥AB,OG∥AB,
∴∠HPC=∠PCD=y,∠OPF=∠OFP=x,
∴∠CPF=x+y,
又∵∠COF=∠PCB
+∠CPF
+∠OFP
=2y+(x+y)+
x
=2x+3y,
∴∠COF+∠OFP=3x+3y=3∠CPF.
图形与坐标单元培优测试卷含解析
一、选择题(共10题;共30分)
1.小李、小王、小张、小谢原有位置如图(横为排、竖为列),小李在第2排第4列,小王在第3排第3列,小张在第4排第2列,小谢在第5排第4列.撤走第一排,仍按照原有确定位置的方法确定新的位置,下列说法正确的是(??
).
A.?小李现在位置为第1排第2列?????????????????????????B.?小张现在位置为第3排第2列
C.?小王现在位置为第2排第2列?????????????????????????D.?小谢现在位置为第4排第2列
2.某学校的平面示意图如图所示,如果宠物店所在位置的坐标为(-2,-3),儿童公园所在位置的坐标为(-4,-2),则(0,4)所在的位置是(???
)
A.?医院?????????????????????????B.?学校???????????????????????C.?汽车站????????????????????D.?水果店
3.如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,C,D的位置时,其中表示错误的是(???
)
A.?A(4,30°)????????????B.?B(2,90°)????????C.?C(6,120°)??????????????D.?D(3,240°)
4.点P在第四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为(??
)
A.?(-3,-2)????????????????B.?(3,-2)????????????????C.?(2,3)???????????????D.?(2,-3)
5.在平面直角坐标系中,将点
向右平移4个单位长度,得到的对应点
的坐标为(???
)
A.??????????????????????????B.????????????????????C.???????????????????D.?
6.在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是(??
)
A.?(1,?1),(?1,?3)????????B.?(1,1),(3,3)???????????C.?(?1,3),(3,1)????????????D.?(3,2),(1,4)
7.已知三角形的三个顶点坐标分别为(-2,1),(2,3),(-3,-1),把这个三角形运动到一个确定位置,在下列各点的坐标中,是经过平移得到的是(?
??)
A.?(0,3),(0,1),(-1,-1)??????????B.?(-3,2),(3,2),(-4,0)
C.?(1,-2),(3,2),(-1,-3)????????D.?(-1,3),(3,5),(-2,1)
8.如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A.?(1,3)??????????????B.?(5,3)?????????????????C.?(6,1)????????????????D.?(8,2)
9.已知点
在第二象限,则m的取值范围在数轴上表示正确的是(?
)
A.????B.?????C.?????D.?
10.如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、……,根据这个规律,第2019个点的坐标为(???
)
A.?(45,10)?????????????????B.?(45,6)?????????????????C.?(45,22)???????????????????D.?(45,0)
二、填空题(共8题;共24分)
11.如图点
A、B
的坐标分别为(1,2)、(3,0),将△AOB
沿
x
轴向右平移,得到△CDE.
已知点
D
在的点
B
左侧,且
DB=1,则点
C
的坐标为
________.
12.若点(3+m
,
a-2)关于y轴对称点的坐标是(3,2),则m+a的值为________.
13.点P到x轴的距离是3,到y轴的距离是5,且在y轴的左侧,则P点的坐标是________
14.在平面直角坐标系中,第二象限内的点
到横轴的距离为2,到纵轴的距离为3,则点
的坐标是________.
15.北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育馆→水立方)。如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为
(-1,0)
,森林公园的坐标为
(-2,3)
,则终点水立方的坐标是________.
16.若点P(-1,a)与Q(b,2)关于x轴对称,则a+b=________.
17.在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点A(1,-2),经过一个变换后对应点为A1
,
经过2个变换后对应点为A2
,
…经过n个变换后对应点为An
,
则用含n的代数式表示点An的坐标为________。
18.如图,所有正方形的中心都在原点,且各边也都与x轴或y轴平行,从内向外,它们的边长依次为2,4,6,8,…顶点依次用A1、A2、A3、A4表示,则顶点A2020的坐标为________.
三、解答题(共6题;共46分)
19.如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).
(1)作ΔABC关于x轴对称的△A1B1C1
,
并写出点A1
,
B1
,
C1的坐标,
(2)作△ABC关于y轴对称的△A2B2C2
,
并写出点A2
,
B2
,
C2的坐标,
(3)观察点A1
,
B1
,
C1和A2
,
B2
,
C2的坐标,请用文字语言归纳点A1和A2
,
B1和B2
,
C1和C2坐标之间的关系.
20.如图,用(-1,0)表示A点的位置,用(2,1)表示B点的位置,那么:
(1)画出直角坐标系。
(2)写出△DEF的三个顶点的坐标。
(3)在图中表示出点M(6,2),N(4,4)的位置。
21.在平面直角坐标系中.
(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4)若AB∥x
轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段
AB
的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
22.如图,在平面直角坐标系中,已知点
,
,
三点.
(1)求
的面积;
(2)如果在第二象限内有一点
,且四边形ABOP的面积是
的面积的两倍;求满足条件的P点坐标.
23.已知点P
(2a﹣10,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值:
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
24.如图1,在平面直角坐标系中,A、B在坐标轴上,其中A(0,a),B(b
,
0)满足|a-3|+
=0.
(1)求A、B两点的坐标;
(2)将AB平移到CD
,
A点对应点C(-2,m),CD交y轴于E
,
若△ABC的面积等于13,求点E的坐标;
(3)如图2,若将AB平移到CD
,
点C、D也在坐标轴上,F为线段AB上一动点,(不包括点A
,
点B),连接OF、FP平分∠BFO
,
∠BCP=2∠PCD
,
试探究∠COF
,
∠OFP
,
∠CPF的数量关系.
答案
一、选择题
1.解:A.
小李现在位置为第1排第4列,故A选项错误;
B.
小张现在位置为第3排第2列,故B选项正确;
C.
小王现在位置为第2排第3列,故C选项错误;
D.
小谢现在位置为第4排第4列,故D选项错误.
故答案为:B.
2.解:根据题意,建立平面直角坐标系如图:
(0,4)所在的位置是学校.
故答案为:B.
3.由题意可知A、B、C、D的坐标可表示为:
A(4,30°),故A不符合题意;
B(2,90°),故B不符合题意;
C(6,120°),故C不符合题意;
D(4,240°),故D符合题意,
故答案为:D.
4.解:∵点P在第四象限,
∴横坐标为3,纵坐标为-2.
故答案为:A
5.解:点A(-2,3)向右平移4个单位长度后得到的对应点A′的坐标为(-2+4,3),
即(2,3),
故答案为:C.
6.解:根据题意可得:将线段AB平移后,A,B的对应点的坐标与原A.
B点的坐标差必须相等.
A.
A点横坐标差为0,纵坐标差为1,B点横坐标差为4,纵坐标差为5,A.
B点对应点的坐标差不相等,故不合题意;
B.
A点横坐标差为0,纵坐标差为?1,B点横坐标差为0,纵坐标差为?1,A.
B点对应点的坐标差相等,故合题意;
C.
A点横坐标差为2,纵坐标差为?3,B点的横坐标差为0,纵坐标差为1,A.
B点对应点的坐标差不相等,故不合题意;
D.
,A点横坐标差为?2,纵坐标差为?2,B点横坐标差为2,纵坐标差为?2,A.
B点对应点的坐标差不相等,故不合题意;
故答案为:B
7.A.由(﹣2,1)到(0,3)是向右平移了2个单位,向上平移了2个单位;而由(2,3)到(0,1)是向左平移了2个单位,向下平移了2个单位,故不符合题意;
B.
由(﹣2,1)到(﹣3,2)是向左平移了1个单位,向上平移了1个单位;而由(2,3)到(3,2)是向右平移了1个单位,向下平移了1个单位,故不符合题意;
C.
由(﹣2,1)到(1,﹣2)是向右平移了3个单位,向下平移了3个单位;而由(2,3)到(3,2)是向右平移了1个单位,向下平移了1个单位,故不符合题意;
D.
由(﹣2,1),(2,3),(﹣3,﹣1)到(﹣1,3),(3,5),(﹣2,1)都是向右平移了1个单位,向上平移了2个单位,故符合题意;
故答案为:D.
8.解:如图所示:“马”位于(6,1).
故答案为:C
.
9.解:∵
点
在第二象限
∴
解之:m>3,m>1
∴m的取值范围是m>3.
故答案为:A.
10.解:将其左侧相连,看作正方形边上的点,如图所示.
边长为0的正方形,有1个点;边长为1的正方形,有3个点;边长为2的正方形,有5个点;…,
∴边长为n的正方形有2n+1个点,
∴边长为n的正方形边上与内部共有1+3+5+…+2n+1=(n+1)2个点.
∵2019=45×45-6,
结合图形即可得知第2019个点的坐标为(45,6).
故答案为:B.
二、填空题
11.解:
的坐标为
,
,
,
,
向右平移了2个单位长度,
点A的坐标为
,
点C的坐标为:
.
故答案是:
.
12.解:∵点(
,
)关于y轴对称点的坐标是(3,2),
∴
,
,
解得:
,
,
∴
,
故答案为:-2.
13.解:∵点P到x轴的距离是3,∴点P的纵坐标是
,
∵点P到y轴的距离是5,且在y轴左侧,∴点P的横坐标是
∴点P的坐标是
或
.
故答案是:
或
.
14.∵点
到横轴的距离为2,到纵轴的距离为3,
∴|y|=2,|x|=3,
由M是第二象限的点,得:
x=?3,y=2.
即点M的坐标是(?3,2),
故答案为:(?3,2).
15.解:根据玲珑塔的坐标可知,原点的坐标位置
∴水立方的坐标为(-2,-3)
16.解:∵点P(-1,a)与Q(b,2)关于x轴对称,
∴b=-1,a=-2
∴a+b=-1-2=-3
故答案为:-3
17.由题意可知:
横坐标每次向右平移一个单位,横坐标依次增加1,2,3……n;
纵坐标每次向上平移三个单位,纵坐标依次增加3,6,9……3n;
即An的坐标表达式为(1+n,
-2+3n)
18.解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4
,
(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数).
∵2020=505×4,
∴A2020(505,﹣505).
故答案为:(505,﹣505).
三、解答题
19.(1)解:如下图所示:
∵A(-1,4),B(-2,2),C(1,1)
A1
,
B1
,
C1和A,B,C关于x轴对称
∴A1(-1,-4),B1(-2,-2),C1(1,-1)
(2)解:如下图所示:
∵A(-1,4),B(-2,2),C(1,1)
A2
,
B2
,
C2和A,B,C关于y轴对称
∴A2(1,4),B2(2,2),C2(-1,1)
(3)解:根据(1)(2)中得出的坐标可知,A1和A2
,
B1和B2
,
C1和C2坐标之间的关系为:横坐标互为相反数,纵坐标也互为相反数.
20.
(1)解:以O点为原点,水平向右为正方向画x轴,垂直往上为正方向画y轴,依此建立直角坐标系即可
(2)解:根据(1)建立的直角坐标系,D(1,2),E(4,3),F(0,4)
(3)解:在(1)建立的直角坐标系标记出点M(6,2)、N(4,4)的位置.
21.
(1)解:根据题意知,2a﹣6=0,解得:a=3,
∴点
P
的坐标为(0,7)
(2)解:∵AB∥x
轴,
∴m﹣1=4,解得
m=5,∵点
B
在第一象限,
∴n+1>0,解得
n>﹣1
(3)解:由(2)知点
A(﹣3,4),
∵AB=6,且点
B
在第一象限,
∴点
B(3,4),
由点
P(0,7)可得
PA2=(﹣3﹣0)2+(4﹣7)2=18、PB2=(3﹣0)2+(4﹣7)2=18,
∵AB2=36,
∴PA2+PB2=AB2
,
且PA=PB,
因此,△PAB是等腰直角三角形。
22.
(1)解:
,
,
,
;
(2)解:
,
,
,
,
,
又
,
,
解得:
,
.
23.
(1)∵点P
(2a﹣10,1﹣a)位于第三象限,
∴1﹣a=﹣3,
∴a=4;
(2)由a=4得:2a﹣12=2×4﹣12=﹣4,
又点Q(x,y)位于第二象限,
所以y>0;
取y=1,得点Q的坐标为(﹣4,1);
(3)∵点P
(2a﹣10,1﹣a)位于第三象限,
∴
,
∴1<a<5,
∵点P的横、纵坐标都是整数,
∴a=2或3或4;
当a=2时,点P(﹣6,﹣1),则PQ>1,
当a=3时,点P(﹣4,﹣2),则PQ>2,
当a=4时,点P(﹣2,﹣3),则PQ>3.
24.
(1)由题意得,a-3=0,b-4=0,
解得,a=3,b=4,
则A(0,3),B(4,0);
(2)如图1所示,
∵DABC的面积等于13,根据A,B,C三点的坐标,
可得:
,(m<0)
解得,m=-2,
则点C的坐标为(-2,-2),
根据平移规律,则有点D的坐标为(2,-5),
设直线CD的解析式为:y=cx+d,
,解得
,
∴CD的解析式为:
,
∴CD与y轴的交点E的坐标为(0,
);
(3)如图2所示,作HP∥AB交AD于H,OG∥AB交FP于G,
设∠OFP=x,∠PCD=y,
则∠BFP=x,∠PCB=2y,
∵HP∥AB,OG∥AB,
∴∠HPC=∠PCD=y,∠OPF=∠OFP=x,
∴∠CPF=x+y,
又∵∠COF=∠PCB
+∠CPF
+∠OFP
=2y+(x+y)+
x
=2x+3y,
∴∠COF+∠OFP=3x+3y=3∠CPF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
