4.1比例线段(2)
图片预览





文档简介
(共19张PPT)
浙教版九年级《数学》上册
表示成
a c
b d
= ,
或 a:b=c:d,
我们把 a、b、c、d 这四个数成比例,
a、d 叫做比例外项,
b、c 叫做比例内项,
如果两个数的比值与另两个数的比值相等,就说这四个数成比例.
(a,b,c,d均不为零)
比例有如下性质:
知识回顾
(2)x:y:z=2:3:4 ,求 的值。
x-y+z
2x+3y-z
(3)已知线段AB=15cm,CD=20cm。求线段AB:CD的值。
(1)若3x=4y,求 、 、 的值。
下列四个数是否成比例,如果能,请写出比例式,并指出比例内项、外项。
1
(1) 5 ,3,6,10
(2) 2,0.5,3,12
(3) 7 ,3,4,8
(4) 2.4,0.8,3.2,0.6
1、把四个数按大小(小大)排列,再看前两个数的比是否等于后两个数的比;
2、把四个数按大小(小大)排列,看最大数与最小数之积是否等于另两数之积.
比例式具有有序性:
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
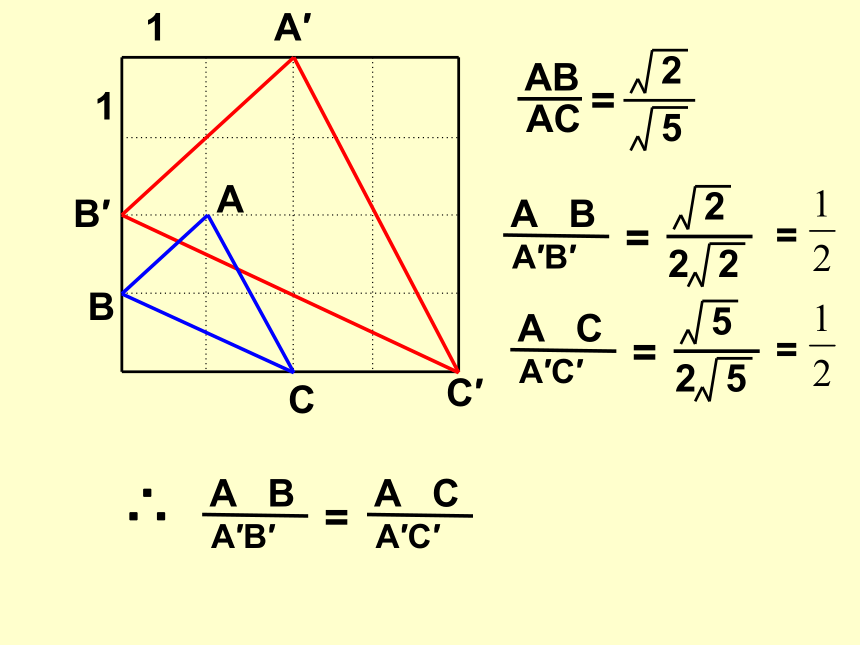
A
B
C
A′
B′
C′
1
1
AB
AC
=
5
2
A B
A′B′
=
2
2
2
=
A C
A′C′
=
5
5
2
=
∴
A B
A′B′
=
A C
A′C′
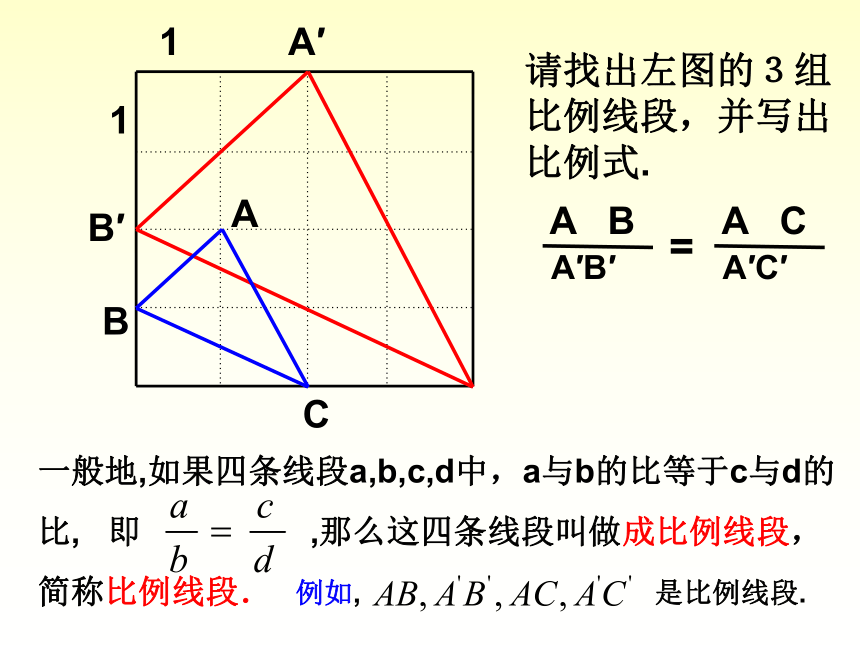
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比, 即 ,那么这四条线段叫做成比例线段,简称比例线段.
请找出左图的3组比例线段,并写出比例式.
A
B
C
A′
B′
1
1
A B
A′B′
=
A C
A′C′
例如, 是比例线段.
例1 已知线段a=10mm , b=6cm,
c=2cm , d=3cm .
问:这四条线段是否成比例?为什么
想一想: 是否还可以写出其他几组成比例的线段.
答:这四条线段成比例.
∵a=10mm=1cm
即线段a、c、d、b成比例.
答:可以.
如:
判断四条线段是否成比例的方法有两种:
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
1.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,下面哪个选项是正确的?( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
2.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
练 习
例2 如图,在直角三角形ABC中,CD是斜边AB上的高线,请找出一组比例线段,并说明理由.
A
B
C
D
分析:(1)根据比例基本性质,要判断四条线段是否成比例,只要采取什么方法
(2)已知条件中有三角形的高,我们通常可以把高与什么知识联系起来?
(3)根据三角形的面积公式,你能得到一个怎样的等式? 根据所得的等式可以写出怎样的比例式。
(看其中两条线段的乘积是否等于另两条线段的乘积)
1、如图,已知AD,CE是△ABC中BC、AB上的高线,求证:AD:CE=AB:BC
试一试
2,如图在平行四边形ABCD中,
.找出图中的一组比例
线段(用小写字母表示),并说明理由.
d
c
b
a
F
E
D
C
B
A
已知A、B两地相距40km,问在比例尺为1:5 000 000的地图上,A、B两地相距多少厘米?
想一想
比例尺=图上距离:实际距离
如图是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
8
注意:求角度时要注意方位。
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
量得图中∠1=28°.
答:基隆市在高雄市的北偏东28°方向,到高雄市的实际距离约为315km。
北
高雄
台南
台中
台北
基隆
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
例4
A
B
C
A′
B′
C ′
比如,量得树AB的影长BC=20m,木杆长A′B′= 1.5m,影长B′C′= 2.5m,
求:树AB的高.
解:在相同时刻的物高与影长成比例
答:树AB的高为12米.
试一试
2 如图,DE是△ABC的中位线,请尽可能多的写出比例线段.
E
D
C
B
A
浙教版九年级《数学》上册
表示成
a c
b d
= ,
或 a:b=c:d,
我们把 a、b、c、d 这四个数成比例,
a、d 叫做比例外项,
b、c 叫做比例内项,
如果两个数的比值与另两个数的比值相等,就说这四个数成比例.
(a,b,c,d均不为零)
比例有如下性质:
知识回顾
(2)x:y:z=2:3:4 ,求 的值。
x-y+z
2x+3y-z
(3)已知线段AB=15cm,CD=20cm。求线段AB:CD的值。
(1)若3x=4y,求 、 、 的值。
下列四个数是否成比例,如果能,请写出比例式,并指出比例内项、外项。
1
(1) 5 ,3,6,10
(2) 2,0.5,3,12
(3) 7 ,3,4,8
(4) 2.4,0.8,3.2,0.6
1、把四个数按大小(小大)排列,再看前两个数的比是否等于后两个数的比;
2、把四个数按大小(小大)排列,看最大数与最小数之积是否等于另两数之积.
比例式具有有序性:
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
A
B
C
A′
B′
C′
1
1
AB
AC
=
5
2
A B
A′B′
=
2
2
2
=
A C
A′C′
=
5
5
2
=
∴
A B
A′B′
=
A C
A′C′
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比, 即 ,那么这四条线段叫做成比例线段,简称比例线段.
请找出左图的3组比例线段,并写出比例式.
A
B
C
A′
B′
1
1
A B
A′B′
=
A C
A′C′
例如, 是比例线段.
例1 已知线段a=10mm , b=6cm,
c=2cm , d=3cm .
问:这四条线段是否成比例?为什么
想一想: 是否还可以写出其他几组成比例的线段.
答:这四条线段成比例.
∵a=10mm=1cm
即线段a、c、d、b成比例.
答:可以.
如:
判断四条线段是否成比例的方法有两种:
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
1.已知线段a=2cm,b=4.1cm,c=4cm,d=8.2cm,下面哪个选项是正确的?( )
A. d, b, a, c成比例线段 B. a, d, b, c成比例线段
C. a, c, b, d成比例线段 D. a, d, c, b成比例线段
2.下列各组线段的长度成比例的是( )
A.2cm,3cm,4cm,1cm B.1.5cm,2.5cm,6.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm D.1cm,2cm,2cm,4cm
C
D
练 习
例2 如图,在直角三角形ABC中,CD是斜边AB上的高线,请找出一组比例线段,并说明理由.
A
B
C
D
分析:(1)根据比例基本性质,要判断四条线段是否成比例,只要采取什么方法
(2)已知条件中有三角形的高,我们通常可以把高与什么知识联系起来?
(3)根据三角形的面积公式,你能得到一个怎样的等式? 根据所得的等式可以写出怎样的比例式。
(看其中两条线段的乘积是否等于另两条线段的乘积)
1、如图,已知AD,CE是△ABC中BC、AB上的高线,求证:AD:CE=AB:BC
试一试
2,如图在平行四边形ABCD中,
.找出图中的一组比例
线段(用小写字母表示),并说明理由.
d
c
b
a
F
E
D
C
B
A
已知A、B两地相距40km,问在比例尺为1:5 000 000的地图上,A、B两地相距多少厘米?
想一想
比例尺=图上距离:实际距离
如图是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
8
注意:求角度时要注意方位。
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
量得图中∠1=28°.
答:基隆市在高雄市的北偏东28°方向,到高雄市的实际距离约为315km。
北
高雄
台南
台中
台北
基隆
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
例4
A
B
C
A′
B′
C ′
比如,量得树AB的影长BC=20m,木杆长A′B′= 1.5m,影长B′C′= 2.5m,
求:树AB的高.
解:在相同时刻的物高与影长成比例
答:树AB的高为12米.
试一试
2 如图,DE是△ABC的中位线,请尽可能多的写出比例线段.
E
D
C
B
A
同课章节目录
